【新课标】1.2.3矩形的性质与判定 课件(共19张PPT)
文档属性
| 名称 | 【新课标】1.2.3矩形的性质与判定 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-16 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
1.2.3矩形的性质与判定
北师版 九年级上册
教学目标
1.掌握矩形的性质及判定方法;
2.会运用矩形的性质及判定方法进行计算和证明;
3.矩形的性质和判定方法与其他有关知识的综合运用.
复习回顾
1.矩形有什么性质?
两组对边分别平行且相等
四个角都是直角
对角线相等且互相平分
轴对称图形
2.怎样判定一个四边形是不是矩形?
有一个角是直角的平行四边形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
新知讲解
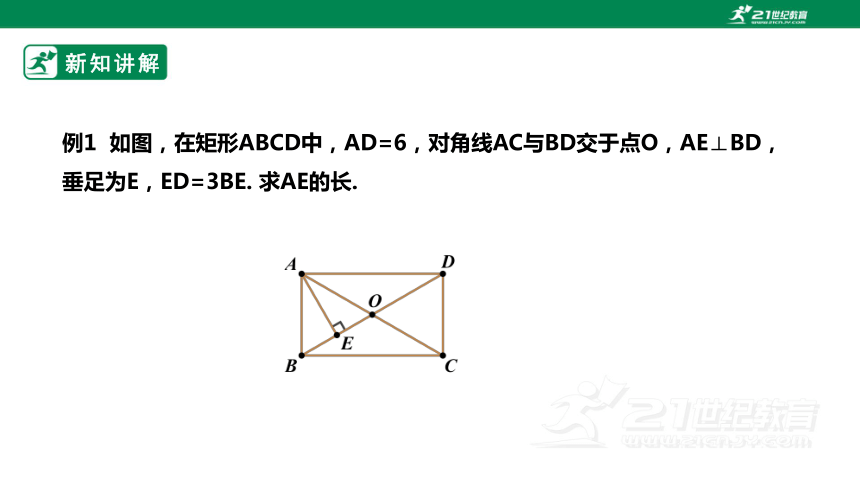
例1 如图,在矩形ABCD中,AD=6,对角线AC与BD交于点O,AE⊥BD,垂足为E,ED=3BE. 求AE的长.
新知讲解
解∵ 四边形 ABCD 是矩形,
∴∠BAD = 90°(矩形的四个都是直角),
AC = BD(矩形的对角线相等)
AO = CO =AC,BO=DO =BD(矩形的对角线互相平分).
∴AO = BO = DO =BD.
∵ED = 3BE,∴BE = OE,
又∵AE⊥BD,∴AB = AO. ∴AB = AO = BO,
即 △ABO是等边三角形. ∴∠ABO = 60°.
∴∠ADB = 90°-∠ABO = 90°- 60°= 30°.
∴AE =AD =×6 = 3.
变式训练
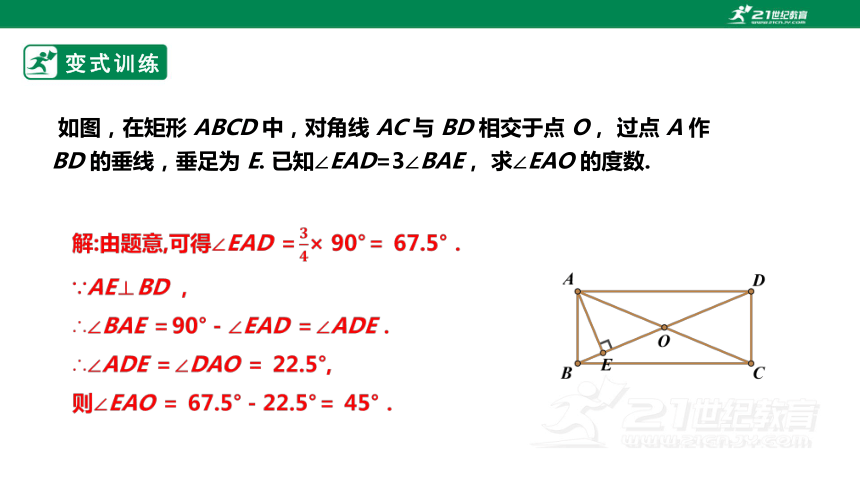
如图,在矩形 ABCD 中,对角线 AC 与 BD 相交于点 O, 过点 A 作 BD 的垂线,垂足为 E. 已知∠EAD=3∠BAE, 求∠EAO 的度数.
解:由题意,可得∠EAD =× 90°= 67.5°.
∵AE⊥BD ,
∴∠BAE =90°-∠EAD =∠ADE.
∴∠ADE =∠DAO = 22.5°,
则∠EAO = 67.5°-22.5°= 45°.
新知讲解
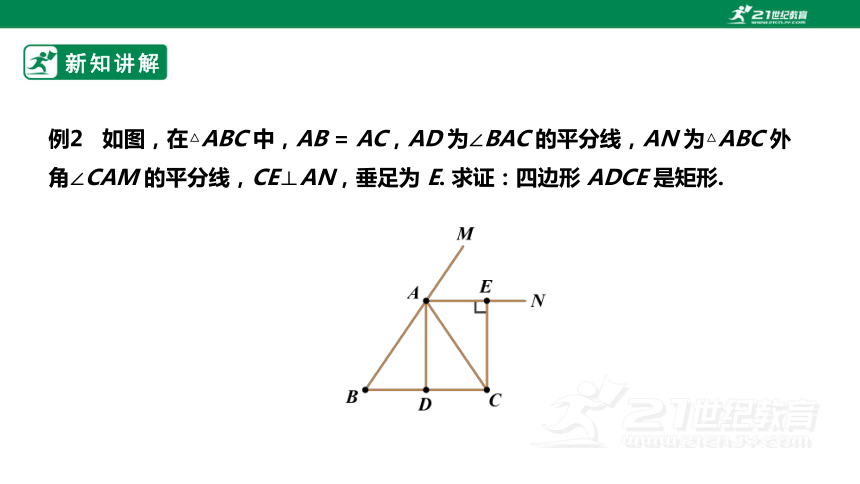
例2 如图,在△ABC 中,AB = AC,AD 为∠BAC 的平分线,AN 为△ABC 外角∠CAM 的平分线,CE⊥AN,垂足为 E. 求证:四边形 ADCE 是矩形.
新知讲解
证明:∵AD 平分∠BAC,AN 平分∠CAM,
∴∠CAD =∠BAC,∠CAN =∠CAM.
∴∠DAE =∠CAD +∠CAN
=(∠BAC +∠CAM)
=×180°= 90°.
在△ABC中,∵AB = AC,AD为∠BAC 的平分线,
∴AD⊥BC. ∴∠ADC = 90°.
又∵CE⊥AN,∴∠CEA = 90° .
∴四边形 ADCE 为矩形(有三个角是直角的四边形是矩形).
新知讲解
在例题中,若连接 DE,交 AC 于点 F.
(1)试判断四边形 ABDE 的形状,并证明你的结论.
(1)四边形 ABDE 是平行四边形,
证明:∵△ABC 是等腰三角形且 AD⊥BC,
∴BD = CD,
又∵ADCE是矩形,∴AE = CD,AE∥CD,
∴BD=AE, BD∥AE,
∴四边形 ABDE 是平行四边形.
(2)线段DF与AB有怎样的关系?证明你的结论.
新知讲解
(2)解:DF∥AB,DF=AB.理由如下:
∵四边形ADCE为矩形,
∴AF=CF,
∵BD=CD,
∴DF是△ABC的中位线,
∴DF∥AB,DF=AB
课堂练习
1.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
D
2.如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF,若CD=6,则AF等于( )
A. B. C. D.8
A
课堂练习
3.如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE=____度.
75
4.如图,在矩形ABCD中,AB=2,BC=4,点A,B分别在y轴,x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标为 .
(1+,2)
课堂练习
5.如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点C与点A重合,请在图中画出折痕,并求折痕的长
E
F
解: 如图,连接EC.在矩形ABCD 中,
AB=6cm, BC=8cm,
∴AC=10cm, ∴AO=CO=5cm.
易证 Rt△AOE ≌ Rt△COE, AE=EC.
由勾股定理,得,
得EC=cm.
∴OE=cm,折痕长 EF=2OE=7.5cm.
O
课堂练习
6.如图,在矩形纸片ABCD 中,AB=3,AD=4,P是 AD上不与 A与D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E,F. 求PE+PF的值.
解:如图,连接PO,在矩形ABCD中
AB=3,AD=4
∴AC=BD=5,OA=OD=
又∵
即
∴
课堂总结
本节课你学到了什么?
(1)用类比的方法探究矩形的性质,先找共性再找特殊性,并注意性质的整合;
(2)矩形的问题常可以转化为直角三角形或等腰三角形的问题来解决.
板书设计
1.2.3 矩形的性质与判定
一、复习
二、根据矩形的性质求线段的长
三、根据矩形的性质求面积
作业布置
【必做题】
教材第18页练习题
【选做题】
教材第19页习题1.6的3、5题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2.3矩形的性质与判定
北师版 九年级上册
教学目标
1.掌握矩形的性质及判定方法;
2.会运用矩形的性质及判定方法进行计算和证明;
3.矩形的性质和判定方法与其他有关知识的综合运用.
复习回顾
1.矩形有什么性质?
两组对边分别平行且相等
四个角都是直角
对角线相等且互相平分
轴对称图形
2.怎样判定一个四边形是不是矩形?
有一个角是直角的平行四边形
对角线相等的平行四边形是矩形
有三个角是直角的四边形是矩形
新知讲解
例1 如图,在矩形ABCD中,AD=6,对角线AC与BD交于点O,AE⊥BD,垂足为E,ED=3BE. 求AE的长.
新知讲解
解∵ 四边形 ABCD 是矩形,
∴∠BAD = 90°(矩形的四个都是直角),
AC = BD(矩形的对角线相等)
AO = CO =AC,BO=DO =BD(矩形的对角线互相平分).
∴AO = BO = DO =BD.
∵ED = 3BE,∴BE = OE,
又∵AE⊥BD,∴AB = AO. ∴AB = AO = BO,
即 △ABO是等边三角形. ∴∠ABO = 60°.
∴∠ADB = 90°-∠ABO = 90°- 60°= 30°.
∴AE =AD =×6 = 3.
变式训练
如图,在矩形 ABCD 中,对角线 AC 与 BD 相交于点 O, 过点 A 作 BD 的垂线,垂足为 E. 已知∠EAD=3∠BAE, 求∠EAO 的度数.
解:由题意,可得∠EAD =× 90°= 67.5°.
∵AE⊥BD ,
∴∠BAE =90°-∠EAD =∠ADE.
∴∠ADE =∠DAO = 22.5°,
则∠EAO = 67.5°-22.5°= 45°.
新知讲解
例2 如图,在△ABC 中,AB = AC,AD 为∠BAC 的平分线,AN 为△ABC 外角∠CAM 的平分线,CE⊥AN,垂足为 E. 求证:四边形 ADCE 是矩形.
新知讲解
证明:∵AD 平分∠BAC,AN 平分∠CAM,
∴∠CAD =∠BAC,∠CAN =∠CAM.
∴∠DAE =∠CAD +∠CAN
=(∠BAC +∠CAM)
=×180°= 90°.
在△ABC中,∵AB = AC,AD为∠BAC 的平分线,
∴AD⊥BC. ∴∠ADC = 90°.
又∵CE⊥AN,∴∠CEA = 90° .
∴四边形 ADCE 为矩形(有三个角是直角的四边形是矩形).
新知讲解
在例题中,若连接 DE,交 AC 于点 F.
(1)试判断四边形 ABDE 的形状,并证明你的结论.
(1)四边形 ABDE 是平行四边形,
证明:∵△ABC 是等腰三角形且 AD⊥BC,
∴BD = CD,
又∵ADCE是矩形,∴AE = CD,AE∥CD,
∴BD=AE, BD∥AE,
∴四边形 ABDE 是平行四边形.
(2)线段DF与AB有怎样的关系?证明你的结论.
新知讲解
(2)解:DF∥AB,DF=AB.理由如下:
∵四边形ADCE为矩形,
∴AF=CF,
∵BD=CD,
∴DF是△ABC的中位线,
∴DF∥AB,DF=AB
课堂练习
1.如图,在矩形ABCD中,对角线AC、BD交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
D
2.如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF,若CD=6,则AF等于( )
A. B. C. D.8
A
课堂练习
3.如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,则∠BOE=____度.
75
4.如图,在矩形ABCD中,AB=2,BC=4,点A,B分别在y轴,x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标为 .
(1+,2)
课堂练习
5.如图,在矩形纸片ABCD中,AB=6cm,BC=8cm,将矩形纸片折叠,使点C与点A重合,请在图中画出折痕,并求折痕的长
E
F
解: 如图,连接EC.在矩形ABCD 中,
AB=6cm, BC=8cm,
∴AC=10cm, ∴AO=CO=5cm.
易证 Rt△AOE ≌ Rt△COE, AE=EC.
由勾股定理,得,
得EC=cm.
∴OE=cm,折痕长 EF=2OE=7.5cm.
O
课堂练习
6.如图,在矩形纸片ABCD 中,AB=3,AD=4,P是 AD上不与 A与D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E,F. 求PE+PF的值.
解:如图,连接PO,在矩形ABCD中
AB=3,AD=4
∴AC=BD=5,OA=OD=
又∵
即
∴
课堂总结
本节课你学到了什么?
(1)用类比的方法探究矩形的性质,先找共性再找特殊性,并注意性质的整合;
(2)矩形的问题常可以转化为直角三角形或等腰三角形的问题来解决.
板书设计
1.2.3 矩形的性质与判定
一、复习
二、根据矩形的性质求线段的长
三、根据矩形的性质求面积
作业布置
【必做题】
教材第18页练习题
【选做题】
教材第19页习题1.6的3、5题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
