2.3.3 点到直线距离 教学设计
文档属性
| 名称 | 2.3.3 点到直线距离 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 247.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 11:59:54 | ||
图片预览


文档简介
2.3.3点到直线距离公式
一、内容和内容解析
1.内容
点到直线的距离公式.
2.内容解析
在前面已经研究了两点间的距离公式、直线方程、两直线的位置关系,同时也介绍了 “以数论形,以形辅数”的数学思想方法. “点到直线的距离”是从初中平面几何的定性作图,过渡到了解析几何的定量计算;《点到直线的距离》的研究,又为以后直线与圆的位置关系和圆锥曲线的进一步学习奠定了基础,具有承前启后的重要作用.
结合以上分析,确定本节课的教学重点:点到直线的距离公式的推导思路分析;点到直线的距离公式的应用.
二、目标和目标解析
1.目标
(1)会用向量工具推导点到直线的距离公式;
(2)掌握点到直线的距离公式,能应用点到直线距离公式解决有关距离问题;
(3)通过点到直线的距离公式的探索和推导过程,培养学生运用等价转化、数形结合等数学思想方法解决问题的能力.
2.目标解析
理解点到直线的距离公式的推导过程;掌握点到直线的距离公式的应用.通过点到直线的距离公式的探索和推导过程,培养学生运用等价转化、数形结合等数学思想方法解决问题的能力,使学生在学会知识的过程中,进一步领会用解析法解决图形性质的能力.通过公式推导思路的探索、评价,优化学生的思维品质,培养学生辩证统一的思想;领会事物之间在一定条件下的转化,用联系的观点看问题,培养学生团队合作精神,培养学生锲而不舍的钻研品质和勇于探究的科学精神.
三、教学问题诊断分析
高二年级学生已掌握了三角函数、平面向量等有关知识,具备了一定的利用解析法研究几何问题的能力.高二学生基础知识较扎实、思维较活跃,但处理抽象问题的能力还有待进一步提高,本课采用类比发现式教学法,启导法、讲练结合法、题组教学法等等.
利用解析法推导公式时,由于字母较多,用运算量大,在具体的运算过程中学生容易产生畏难情绪,半途而废;采取课前预习,小组讨论,学生展示等手段加以突破.对于几何法中的构造直角三角形学生感到比较困难;采取利用复习两点间距离公式的推导复习,利用类比教学法加以突破;对于几向量法学生不容易想到,采取启导法,小组讨论法,让学生领会“设点不求点”的解题思路.本节课的教学难点点到直线的距离公式的推导不同方法的思路分析.
四、教学过程设计
(一)创设情境,引入新课
问题1:在铁路附近有一个仓库,现在需要铺设一条连接仓库和铁路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短
师生活动:学生独立思考.将实际问题抽象成数学问题.
问题2:设点,直线 : ,
如何求点P到直线L的距离?
设计意图:以实际问题为背景来引课,激发学生学习数学的热情和兴趣.通过生活中点到直线距离的问题情境,引出在坐标系下探究点到直线距离公式的问题.
(二)转化探究,获得新知
如图,点到直线的距离,是指从点到直线的垂线段的长度,其中是垂足.
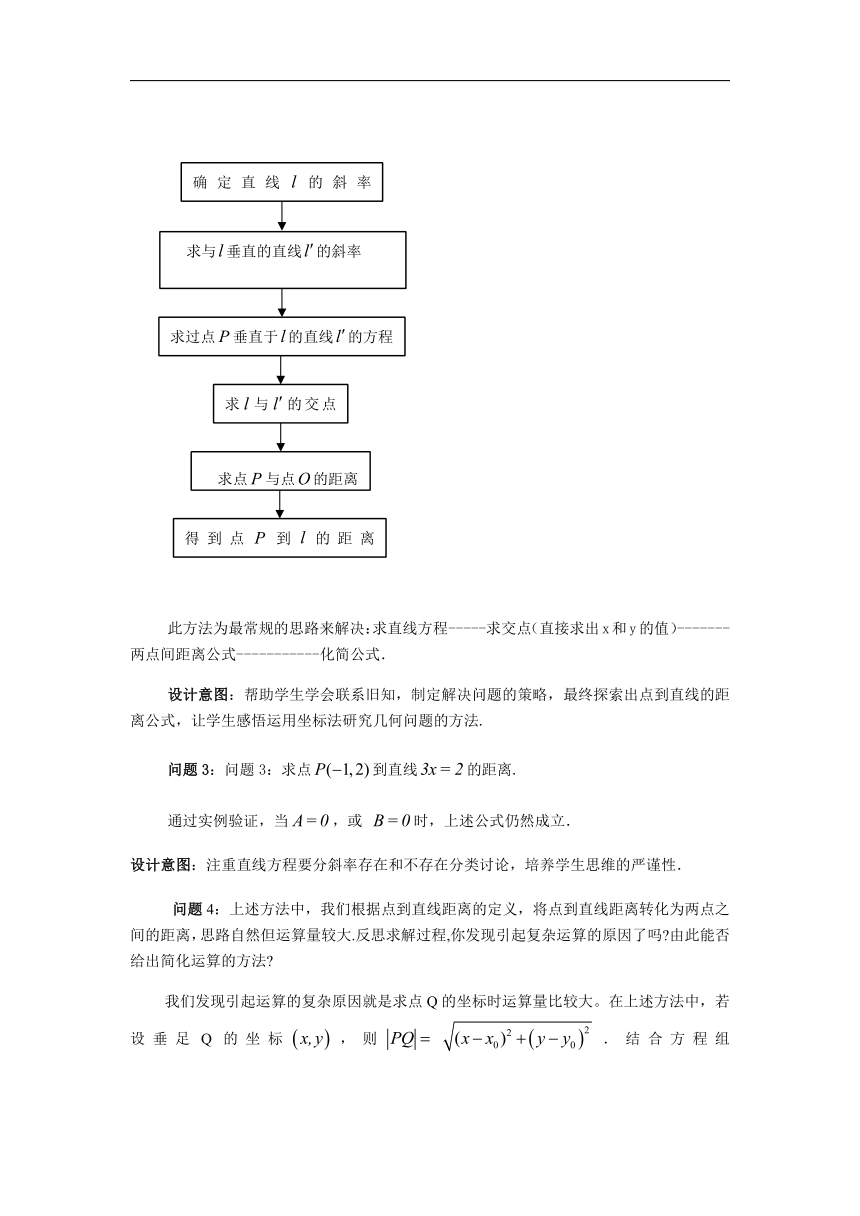
思路:
此方法为最常规的思路来解决:求直线方程-----求交点(直接求出x和y的值)-------两点间距离公式-----------化简公式.
设计意图:帮助学生学会联系旧知,制定解决问题的策略,最终探索出点到直线的距离公式,让学生感悟运用坐标法研究几何问题的方法.
问题3:问题3:求点到直线的距离.
通过实例验证,当,或 时,上述公式仍然成立.
设计意图:注重直线方程要分斜率存在和不存在分类讨论,培养学生思维的严谨性.
问题4:上述方法中,我们根据点到直线距离的定义,将点到直线距离转化为两点之间的距离,思路自然但运算量较大.反思求解过程,你发现引起复杂运算的原因了吗 由此能否给出简化运算的方法
我们发现引起运算的复杂原因就是求点Q的坐标时运算量比较大。在上述方法中,若设垂足Q的坐标,则.结合方程组 ,我们能直接求出,进而求出.
设计意图:求简是数学追求的一个主要目标,培养学生的求简意识.介绍设而不求的思想方法.
问题5:我们知道,向量是解决距离、角度问题的有力工具。能否用向量方法求点到直线的距离?
如图,点P到直线l的距离,就是向量的模,设是直线l上的任意一点, 是与直线l的方向向量垂直的单位向量,则是在上的投影向量, =.
思考:如何利用直线l的方程得到与的方向向量垂直的单位向量?
设直线l:上的任意两点,则是直线l的方向向量。把, 两式相减,得 ,由平面向量的数量积运算可知,向量与向量垂直,向量 就是与直线的方向向量垂直的一个单位向量的单位向量,我们取 ,
从而= =
因为点在直线l上所以代入上式,
得=
因此=
思考:比较上述两种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;第二种方法利用向量投影,通过向量运算求出结果,简化了运算,除了上述两种方法,你还有其他推导方法吗?
设计意图:通过不同方法推导点到直线的距离公式,体会算法的多样性,同时比较不同推导方法,比较算法的优劣,优化思维品质,发展学生数学运算,数学抽象和数学建模的核心素养.
问题6:比较上述两种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;第二种方法利用向量投影,通过向量运算求出结果,简化了运算,除了上述两种方法,你还有其他推导方法吗?
先添作辅助线,过点作轴、轴的垂线交于点,再利用直角三角形的面积公式进行计算.
(三)例题讲解,学以致用
问题7:已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积.
设计意图:通过直接将已知点的坐标代人公式计算,强调公式的形式记忆.在典例分析和练习中熟悉公式的基本结构,并体会点到直线距离公式的初步应用.发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养.
(四)归纳总结,布置作业
教师引导学生回顾本节知识.
设计意图:从知识内容和研究方法两个方面对本节课进行小结.
布置作业:教科书P77练习1,2,3.
目标检测设计
1.点(1,-1)到直线y=1的距离是( )
A. B. C.3 D.2
解析:d==2,故选D.
答案:D
2.已知点A(-3,-4),B(6,3)到直线l:ax+y+1=0的距离相等,则实数a的值等于( )
A. B.-
C.-或- D.-
解析:由点到直线的距离公式可得,化简得|3a+3|=|6a+4|,解得实数a=-或-.故选C.
答案:C
3.直线3x-4y-27=0上到点P(2,1)距离最近的点的坐标是( ).
解析:由题意知过点P作直线3x-4y-27=0的垂线,
设垂足为M,则|MP|最小,
直线MP的方程为y-1=-(x-2),
解方程组
∴所求点的坐标为(5,-3).
答案:(5,-3)
设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养.
一、内容和内容解析
1.内容
点到直线的距离公式.
2.内容解析
在前面已经研究了两点间的距离公式、直线方程、两直线的位置关系,同时也介绍了 “以数论形,以形辅数”的数学思想方法. “点到直线的距离”是从初中平面几何的定性作图,过渡到了解析几何的定量计算;《点到直线的距离》的研究,又为以后直线与圆的位置关系和圆锥曲线的进一步学习奠定了基础,具有承前启后的重要作用.
结合以上分析,确定本节课的教学重点:点到直线的距离公式的推导思路分析;点到直线的距离公式的应用.
二、目标和目标解析
1.目标
(1)会用向量工具推导点到直线的距离公式;
(2)掌握点到直线的距离公式,能应用点到直线距离公式解决有关距离问题;
(3)通过点到直线的距离公式的探索和推导过程,培养学生运用等价转化、数形结合等数学思想方法解决问题的能力.
2.目标解析
理解点到直线的距离公式的推导过程;掌握点到直线的距离公式的应用.通过点到直线的距离公式的探索和推导过程,培养学生运用等价转化、数形结合等数学思想方法解决问题的能力,使学生在学会知识的过程中,进一步领会用解析法解决图形性质的能力.通过公式推导思路的探索、评价,优化学生的思维品质,培养学生辩证统一的思想;领会事物之间在一定条件下的转化,用联系的观点看问题,培养学生团队合作精神,培养学生锲而不舍的钻研品质和勇于探究的科学精神.
三、教学问题诊断分析
高二年级学生已掌握了三角函数、平面向量等有关知识,具备了一定的利用解析法研究几何问题的能力.高二学生基础知识较扎实、思维较活跃,但处理抽象问题的能力还有待进一步提高,本课采用类比发现式教学法,启导法、讲练结合法、题组教学法等等.
利用解析法推导公式时,由于字母较多,用运算量大,在具体的运算过程中学生容易产生畏难情绪,半途而废;采取课前预习,小组讨论,学生展示等手段加以突破.对于几何法中的构造直角三角形学生感到比较困难;采取利用复习两点间距离公式的推导复习,利用类比教学法加以突破;对于几向量法学生不容易想到,采取启导法,小组讨论法,让学生领会“设点不求点”的解题思路.本节课的教学难点点到直线的距离公式的推导不同方法的思路分析.
四、教学过程设计
(一)创设情境,引入新课
问题1:在铁路附近有一个仓库,现在需要铺设一条连接仓库和铁路的道路.请同学们帮助设计一下:在理论上怎样铺路可以使这条连接道路的长度最短
师生活动:学生独立思考.将实际问题抽象成数学问题.
问题2:设点,直线 : ,
如何求点P到直线L的距离?
设计意图:以实际问题为背景来引课,激发学生学习数学的热情和兴趣.通过生活中点到直线距离的问题情境,引出在坐标系下探究点到直线距离公式的问题.
(二)转化探究,获得新知
如图,点到直线的距离,是指从点到直线的垂线段的长度,其中是垂足.
思路:
此方法为最常规的思路来解决:求直线方程-----求交点(直接求出x和y的值)-------两点间距离公式-----------化简公式.
设计意图:帮助学生学会联系旧知,制定解决问题的策略,最终探索出点到直线的距离公式,让学生感悟运用坐标法研究几何问题的方法.
问题3:问题3:求点到直线的距离.
通过实例验证,当,或 时,上述公式仍然成立.
设计意图:注重直线方程要分斜率存在和不存在分类讨论,培养学生思维的严谨性.
问题4:上述方法中,我们根据点到直线距离的定义,将点到直线距离转化为两点之间的距离,思路自然但运算量较大.反思求解过程,你发现引起复杂运算的原因了吗 由此能否给出简化运算的方法
我们发现引起运算的复杂原因就是求点Q的坐标时运算量比较大。在上述方法中,若设垂足Q的坐标,则.结合方程组 ,我们能直接求出,进而求出.
设计意图:求简是数学追求的一个主要目标,培养学生的求简意识.介绍设而不求的思想方法.
问题5:我们知道,向量是解决距离、角度问题的有力工具。能否用向量方法求点到直线的距离?
如图,点P到直线l的距离,就是向量的模,设是直线l上的任意一点, 是与直线l的方向向量垂直的单位向量,则是在上的投影向量, =.
思考:如何利用直线l的方程得到与的方向向量垂直的单位向量?
设直线l:上的任意两点,则是直线l的方向向量。把, 两式相减,得 ,由平面向量的数量积运算可知,向量与向量垂直,向量 就是与直线的方向向量垂直的一个单位向量的单位向量,我们取 ,
从而= =
因为点在直线l上所以代入上式,
得=
因此=
思考:比较上述两种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;第二种方法利用向量投影,通过向量运算求出结果,简化了运算,除了上述两种方法,你还有其他推导方法吗?
设计意图:通过不同方法推导点到直线的距离公式,体会算法的多样性,同时比较不同推导方法,比较算法的优劣,优化思维品质,发展学生数学运算,数学抽象和数学建模的核心素养.
问题6:比较上述两种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;第二种方法利用向量投影,通过向量运算求出结果,简化了运算,除了上述两种方法,你还有其他推导方法吗?
先添作辅助线,过点作轴、轴的垂线交于点,再利用直角三角形的面积公式进行计算.
(三)例题讲解,学以致用
问题7:已知点A(1,3),B(3,1),C(-1,0),求△ABC的面积.
设计意图:通过直接将已知点的坐标代人公式计算,强调公式的形式记忆.在典例分析和练习中熟悉公式的基本结构,并体会点到直线距离公式的初步应用.发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养.
(四)归纳总结,布置作业
教师引导学生回顾本节知识.
设计意图:从知识内容和研究方法两个方面对本节课进行小结.
布置作业:教科书P77练习1,2,3.
目标检测设计
1.点(1,-1)到直线y=1的距离是( )
A. B. C.3 D.2
解析:d==2,故选D.
答案:D
2.已知点A(-3,-4),B(6,3)到直线l:ax+y+1=0的距离相等,则实数a的值等于( )
A. B.-
C.-或- D.-
解析:由点到直线的距离公式可得,化简得|3a+3|=|6a+4|,解得实数a=-或-.故选C.
答案:C
3.直线3x-4y-27=0上到点P(2,1)距离最近的点的坐标是( ).
解析:由题意知过点P作直线3x-4y-27=0的垂线,
设垂足为M,则|MP|最小,
直线MP的方程为y-1=-(x-2),
解方程组
∴所求点的坐标为(5,-3).
答案:(5,-3)
设计意图:通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、直观想象、数学建模的核心素养.
