3.1.2 椭圆的简单几何性质(第一课时)教案
文档属性
| 名称 | 3.1.2 椭圆的简单几何性质(第一课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 11:59:54 | ||
图片预览


文档简介
3.1.2椭圆的简单几何性质(第一课时)
(人教A版选择性必修数学第一册第三章圆锥曲线的方程)
一、教学目标
1.掌握椭圆的范围、对称性、中心、顶点、轴、离心率等几何性质,
能够应用椭圆的标准方程研究椭圆的几何性质。
2.会根据椭圆的几何性质求椭圆的标准方程
二、教学重难点
1.学会椭圆的长短轴、焦点坐标、离心率的基本概念
2.掌握椭圆的离心率、长短轴的定义基础及其灵活应用
三、教学过程
1.椭圆的简单几何性质
1.1创设情境,引发思考
【实际情境】神舟飞船发射成功,飞行轨道具有何种特征?
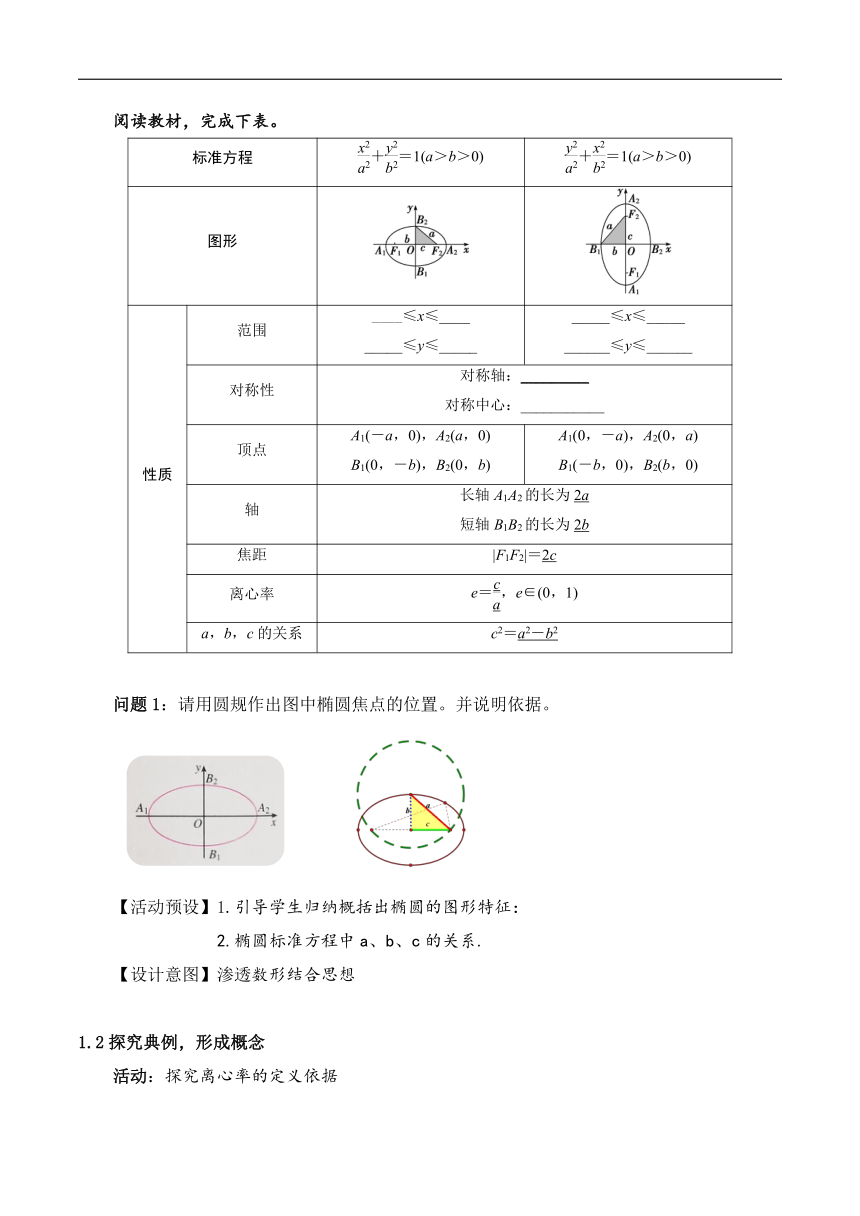
阅读教材,完成下表。
标准方程 +=1(a>b>0) +=1(a>b>0)
图形
性质 范围 ____≤x≤____ _____≤y≤_____ _____≤x≤_____ ______≤y≤______
对称性 对称轴:_________ 对称中心:___________
顶点 A1(-a,0),A2(a,0) B1(0,-b),B2(0,b) A1(0,-a),A2(0,a) B1(-b,0),B2(b,0)
轴 长轴A1A2的长为2a 短轴B1B2的长为2b
焦距 |F1F2|=2c
离心率 e=,e∈(0,1)
a,b,c的关系 c2=a2-b2
问题1:请用圆规作出图中椭圆焦点的位置。并说明依据。
【活动预设】1.引导学生归纳概括出椭圆的图形特征:
2.椭圆标准方程中a、b、c的关系.
【设计意图】渗透数形结合思想
1.2探究典例,形成概念
活动:探究离心率的定义依据
【活动预设】求适合下列条件的椭圆的焦点坐标和离心率:
【设计意图】为数学概念的形成提供理论依据.
问题2:求适合下列条件的椭圆的长短轴、焦点坐标和离心率:
【活动预设】探究焦点位置与标准方程之间联系。
【设计意图】比较不同的焦点位置对图形的影响
1.3具体感知,理性分析
活动:自主举例的接龙活动.
【活动要求】分成A、B组:A组给出标准方程B组画出椭圆的图像并说明特征;然后交换:A组给出椭圆的图形B组写出标准方程。
【活动预设】对椭圆的标准方程的形式给出清晰的认识
【设计意图】
在形成椭圆概念后,遵循从一般到特殊的思路,在实践活动中进行再认识,熟悉概念,从外延的角度加深概念的理解,从而形成数形结合的思想用标准方程研究椭圆的几何性质。。
2.初步应用,理解概念
例1 求椭圆16x2+25y2=400旳长轴长短轴长,离心率,焦点和顶点坐标
【预设的答案】16x2+25y2=400是否为标准方程?
【设计意图】对椭圆方程的结构认识。
【数学情境】比较方程mx2+ny2=mn;+=1(a>b>0)的区别与联系
【预设的答案】
或
【设计意图】
(1)对于焦点位置不同,方程的形式之间的区别与联系;
(2)a,b,c,e之间的关系
【设计意图】
(1)对于图形上的特征,培养观察分析能力;
(2)培养分类讨论思想。
3.归纳小结,文化渗透
【设计意图】
(1)梳理本节课对于椭圆的几何性质认知;
(2)进行数学文化渗透,鼓励学生积极攀登知识高峰,进一步体会学习椭圆的必要性 .
四、课外作业
作业教程P1121-5
(人教A版选择性必修数学第一册第三章圆锥曲线的方程)
一、教学目标
1.掌握椭圆的范围、对称性、中心、顶点、轴、离心率等几何性质,
能够应用椭圆的标准方程研究椭圆的几何性质。
2.会根据椭圆的几何性质求椭圆的标准方程
二、教学重难点
1.学会椭圆的长短轴、焦点坐标、离心率的基本概念
2.掌握椭圆的离心率、长短轴的定义基础及其灵活应用
三、教学过程
1.椭圆的简单几何性质
1.1创设情境,引发思考
【实际情境】神舟飞船发射成功,飞行轨道具有何种特征?
阅读教材,完成下表。
标准方程 +=1(a>b>0) +=1(a>b>0)
图形
性质 范围 ____≤x≤____ _____≤y≤_____ _____≤x≤_____ ______≤y≤______
对称性 对称轴:_________ 对称中心:___________
顶点 A1(-a,0),A2(a,0) B1(0,-b),B2(0,b) A1(0,-a),A2(0,a) B1(-b,0),B2(b,0)
轴 长轴A1A2的长为2a 短轴B1B2的长为2b
焦距 |F1F2|=2c
离心率 e=,e∈(0,1)
a,b,c的关系 c2=a2-b2
问题1:请用圆规作出图中椭圆焦点的位置。并说明依据。
【活动预设】1.引导学生归纳概括出椭圆的图形特征:
2.椭圆标准方程中a、b、c的关系.
【设计意图】渗透数形结合思想
1.2探究典例,形成概念
活动:探究离心率的定义依据
【活动预设】求适合下列条件的椭圆的焦点坐标和离心率:
【设计意图】为数学概念的形成提供理论依据.
问题2:求适合下列条件的椭圆的长短轴、焦点坐标和离心率:
【活动预设】探究焦点位置与标准方程之间联系。
【设计意图】比较不同的焦点位置对图形的影响
1.3具体感知,理性分析
活动:自主举例的接龙活动.
【活动要求】分成A、B组:A组给出标准方程B组画出椭圆的图像并说明特征;然后交换:A组给出椭圆的图形B组写出标准方程。
【活动预设】对椭圆的标准方程的形式给出清晰的认识
【设计意图】
在形成椭圆概念后,遵循从一般到特殊的思路,在实践活动中进行再认识,熟悉概念,从外延的角度加深概念的理解,从而形成数形结合的思想用标准方程研究椭圆的几何性质。。
2.初步应用,理解概念
例1 求椭圆16x2+25y2=400旳长轴长短轴长,离心率,焦点和顶点坐标
【预设的答案】16x2+25y2=400是否为标准方程?
【设计意图】对椭圆方程的结构认识。
【数学情境】比较方程mx2+ny2=mn;+=1(a>b>0)的区别与联系
【预设的答案】
或
【设计意图】
(1)对于焦点位置不同,方程的形式之间的区别与联系;
(2)a,b,c,e之间的关系
【设计意图】
(1)对于图形上的特征,培养观察分析能力;
(2)培养分类讨论思想。
3.归纳小结,文化渗透
【设计意图】
(1)梳理本节课对于椭圆的几何性质认知;
(2)进行数学文化渗透,鼓励学生积极攀登知识高峰,进一步体会学习椭圆的必要性 .
四、课外作业
作业教程P1121-5
