人教版九年级上册21.2.1 配方法 课件 (共15张PPT)
文档属性
| 名称 | 人教版九年级上册21.2.1 配方法 课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 802.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 20:17:19 | ||
图片预览






文档简介
(共15张PPT)
21.2.1 配方法
1.求出下列各数的平方根。
2.完全平方公式
知识回顾
3.填空
(1) 9x2=1 ;
(2) (x-2)2=2.
2.下列方程能用直接开平方法来解吗
1.用直接开平方法解下列方程:
(1) x2+6x+9 =5;
(2)x2+6x+4=0.
把两题转化成(x+n)2=p(p≥0)的
形式,再利用开平方
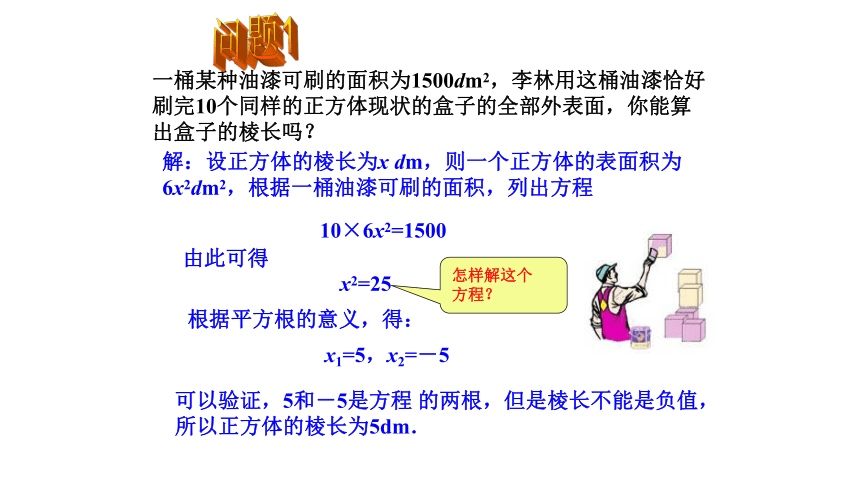
一桶某种油漆可刷的面积为1500dm2,李林用这桶油漆恰好刷完10个同样的正方体现状的盒子的全部外表面,你能算出盒子的棱长吗?
10×6x2=1500
由此可得
x2=25
根据平方根的意义,得:
x1=5,x2=-5
可以验证,5和-5是方程 的两根,但是棱长不能是负值,所以正方体的棱长为5dm.
解:设正方体的棱长为x dm,则一个正方体的表面积为6x2dm2,根据一桶油漆可刷的面积,列出方程
怎样解这个
方程?
问题1
练一练
(1)方程 的根是 .
(2)方程 的根是 .
(3)方程 的根是 .
2. 选择适当的方法解下列方程:
(1)x2-81=0 (2)2x2=50
(3)(x+1)2=4
x1=0.5,x2=-0.5
x1=3,x2=-3
x1=2,x2=-1
1.填一填:
x=±9
x=±5
x1=1,x2=-3
回顾与归纳
一般地,对于方程 X2=P,
当P>0时,根据平方根的意义,此方程有两个不相等的实数根,即:
(2) 当P=0时,此方程有两个相等的实数根,
即:
(3)当P<0时,因为对任意实数X,都有x2 ≥0,所以此方程无实数根,即:
例1: 用配方法解方程
解:
配方,得:
开平方,得:
移项,得:
∴原方程的解为:
例2: 你能用配方法解方程
吗?
解:
配方,得:
开平方,得:
范例研讨运用新知
移项,得:
∴原方程的解为:
二次项系数化为1,得:
二次项系数不为1
又怎么办
★一移、二化、三配、四开、五定.
“配方法”解方程的基本步骤:
4.开方(降次):利用开平方法化为两个一元一次方程.
3.配方:把方程的左边配成一个完全平方式;
1.移项:常数项移到方程的右边;
梳理总结
并整理:把方程的转化为 的形式;
5.定解:确定此一元二次方程的解.
2.化 1:把二次项系数化为1
(1)x2-8x+1=0
(1)解:移项,得:x2-8x=-1
配方,得:x2-8x+42=-1+42
(x-4)2=15
趁热打铁
(2) 2x2+1=3x
(2) 解:移项,得:2x2-3x=-1
二次项系数化为1,得:
配方,得:
解下列方程:
(1)x2+4x-9=2x-11;(2)x(x+4)=8x+12;
解:x2+2x+2=0,
(x+1)2=-1.
此方程无解;
解:x2-4x-12=0,
(x-2)2=16.
x1=6,x2=-2;
难点巩固
课堂练习
强化练习:
配方法
定义
通过配成完全平方形式解一元二次方程的方法.
步骤
一移常数项;
二配方[配上 ];
三写成(x+n)2=p (p ≥0);
四直接开平方法解方程.
特别提醒:
在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
小结
21.2.1 配方法
1.求出下列各数的平方根。
2.完全平方公式
知识回顾
3.填空
(1) 9x2=1 ;
(2) (x-2)2=2.
2.下列方程能用直接开平方法来解吗
1.用直接开平方法解下列方程:
(1) x2+6x+9 =5;
(2)x2+6x+4=0.
把两题转化成(x+n)2=p(p≥0)的
形式,再利用开平方
一桶某种油漆可刷的面积为1500dm2,李林用这桶油漆恰好刷完10个同样的正方体现状的盒子的全部外表面,你能算出盒子的棱长吗?
10×6x2=1500
由此可得
x2=25
根据平方根的意义,得:
x1=5,x2=-5
可以验证,5和-5是方程 的两根,但是棱长不能是负值,所以正方体的棱长为5dm.
解:设正方体的棱长为x dm,则一个正方体的表面积为6x2dm2,根据一桶油漆可刷的面积,列出方程
怎样解这个
方程?
问题1
练一练
(1)方程 的根是 .
(2)方程 的根是 .
(3)方程 的根是 .
2. 选择适当的方法解下列方程:
(1)x2-81=0 (2)2x2=50
(3)(x+1)2=4
x1=0.5,x2=-0.5
x1=3,x2=-3
x1=2,x2=-1
1.填一填:
x=±9
x=±5
x1=1,x2=-3
回顾与归纳
一般地,对于方程 X2=P,
当P>0时,根据平方根的意义,此方程有两个不相等的实数根,即:
(2) 当P=0时,此方程有两个相等的实数根,
即:
(3)当P<0时,因为对任意实数X,都有x2 ≥0,所以此方程无实数根,即:
例1: 用配方法解方程
解:
配方,得:
开平方,得:
移项,得:
∴原方程的解为:
例2: 你能用配方法解方程
吗?
解:
配方,得:
开平方,得:
范例研讨运用新知
移项,得:
∴原方程的解为:
二次项系数化为1,得:
二次项系数不为1
又怎么办
★一移、二化、三配、四开、五定.
“配方法”解方程的基本步骤:
4.开方(降次):利用开平方法化为两个一元一次方程.
3.配方:把方程的左边配成一个完全平方式;
1.移项:常数项移到方程的右边;
梳理总结
并整理:把方程的转化为 的形式;
5.定解:确定此一元二次方程的解.
2.化 1:把二次项系数化为1
(1)x2-8x+1=0
(1)解:移项,得:x2-8x=-1
配方,得:x2-8x+42=-1+42
(x-4)2=15
趁热打铁
(2) 2x2+1=3x
(2) 解:移项,得:2x2-3x=-1
二次项系数化为1,得:
配方,得:
解下列方程:
(1)x2+4x-9=2x-11;(2)x(x+4)=8x+12;
解:x2+2x+2=0,
(x+1)2=-1.
此方程无解;
解:x2-4x-12=0,
(x-2)2=16.
x1=6,x2=-2;
难点巩固
课堂练习
强化练习:
配方法
定义
通过配成完全平方形式解一元二次方程的方法.
步骤
一移常数项;
二配方[配上 ];
三写成(x+n)2=p (p ≥0);
四直接开平方法解方程.
特别提醒:
在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
小结
同课章节目录
