人教版九年级上册21.2.3 因式分解法 课件 (共16张PPT)
文档属性
| 名称 | 人教版九年级上册21.2.3 因式分解法 课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 946.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
21.2.3 因式分解法
PART ONE
温故知新
1.我们已经学过了几种解一元二次方程的方法
2.什么叫因式分解
把一个多项式分解成几个整式乘积的形式叫做因式分解.
直接开平方法
配方法
x2=a (a≥0)
(x+m)2=n (n≥0)
公式法
有哪些常见形式?
PART ONE
温故知新
输入标
分解因式的常见形式
(1)提取公因式法:
(2)公式法:
am+bm+cm=m(a+b+c)
a2-b2=(a+b)(a-b), a2+2ab+b2=(a+b)2
PART TWO
合作探究
提取公因式
观察式子特点
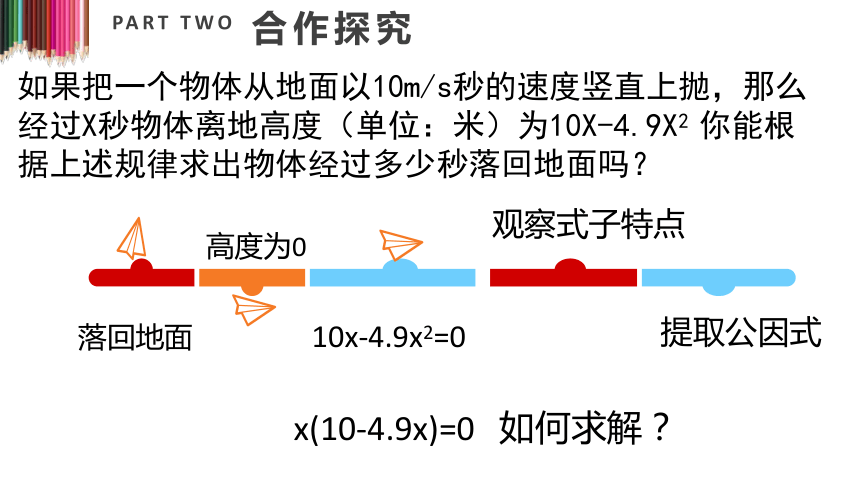
10x-4.9x2=0
高度为0
落回地面
如果把一个物体从地面以10m/s秒的速度竖直上抛,那么经过X秒物体离地高度(单位:米)为10X-4.9X2 你能根据上述规律求出物体经过多少秒落回地面吗?
x(10-4.9x)=0 如何求解?
PART TWO
合作探究
请在此处输入具体描述内容,文字尽量言简意赅,说明意思即可,不必过于繁琐,注意版面的美观度。请在此处输入具体描述内容,文字尽量言简意赅,说明意思即可,不必过于繁琐,注意版面的美观度。
请输入标题
x(10-4.9x)=0
x=0 或
10-4.9x=0 解得
x=0
或 x=
知识链接:
如果a·b=0
那么
a=0或b=0.
可以发现,由①到②的过程,不是用开方降次,而是先因式分解使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次,这种解法叫做因式分解法.
以上解方程 x(10-4.9x)=0 的方法是如何使二次方程降为一次的?
PART TWO
合作探究
①
②
解方程:例 1、(x+3)(x-1)=-7
解:原方程可变形为:
(x+2) =0
x+2=0或x+2=0
∴ x1=-2 ,x2=-2
x2+2x+4 =0
左边分解成两个一次因式 的乘积
至少有一个一次因式为零得到两个一元一次方程
两个一元一次方程的解就是原方程的解
方程右边化为零
例题讲解
简记歌决:
右化零,左分解
两因式,各求解
例2、(3x+1)2-4= 0
解:原方程可变形为
平方差公式.
例题讲解
反过来:
(x+p)(x+q)
x
x
3
-6
小结:(1).因式分解竖直写;
(2).交叉相乘验中项;
3x-6x=-3x
(3).横向写出两因式.
(x+3)和(x-6)
解:原式=
(x+3)
(x-6)
想一想:
2、把
x
x
5
3
(x+5)
(x+3)
a
a
-5
-9
解:
(a-5)(a-9)=0
a-5=o或a-9=0
5x+3x=8x
-5a-9a=-14a
例题讲解
十字相乘法
(1)x +12x=0 (2) x +2x+1 = 1;
精讲实练
用分解因式法解方程:
完全平方公式.
提公因式.
(3)x2+6x-7=0
精讲实练
-x+7x=6x
十字相乘法
1.解下列方程:解: 因式分解,得(1)x2+x=0x(x+1 ) = 0.得x= 0或x+ 1 =0,x1=0 ,x2=-1.解:因式分解,得练习1解:化为一般式为因式分解,得x2-2x+1 = 0.(x-1 )(x-1 ) = 0.有x-1 = 0或x-1 = 0,x1=x2=1.解:因式分解,得( 2x+ 11 )( 2x-11 ) = 0.有2x+ 11 = 0或2x-11= 0,12.把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,求小圆形场地的半径.解:设小圆形场地的半径为r根据题意(r+ 5 )2×π=2r2π.因式分解,得于是得答:小圆形场地的半径是1
21.2.3 因式分解法
PART ONE
温故知新
1.我们已经学过了几种解一元二次方程的方法
2.什么叫因式分解
把一个多项式分解成几个整式乘积的形式叫做因式分解.
直接开平方法
配方法
x2=a (a≥0)
(x+m)2=n (n≥0)
公式法
有哪些常见形式?
PART ONE
温故知新
输入标
分解因式的常见形式
(1)提取公因式法:
(2)公式法:
am+bm+cm=m(a+b+c)
a2-b2=(a+b)(a-b), a2+2ab+b2=(a+b)2
PART TWO
合作探究
提取公因式
观察式子特点
10x-4.9x2=0
高度为0
落回地面
如果把一个物体从地面以10m/s秒的速度竖直上抛,那么经过X秒物体离地高度(单位:米)为10X-4.9X2 你能根据上述规律求出物体经过多少秒落回地面吗?
x(10-4.9x)=0 如何求解?
PART TWO
合作探究
请在此处输入具体描述内容,文字尽量言简意赅,说明意思即可,不必过于繁琐,注意版面的美观度。请在此处输入具体描述内容,文字尽量言简意赅,说明意思即可,不必过于繁琐,注意版面的美观度。
请输入标题
x(10-4.9x)=0
x=0 或
10-4.9x=0 解得
x=0
或 x=
知识链接:
如果a·b=0
那么
a=0或b=0.
可以发现,由①到②的过程,不是用开方降次,而是先因式分解使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次,这种解法叫做因式分解法.
以上解方程 x(10-4.9x)=0 的方法是如何使二次方程降为一次的?
PART TWO
合作探究
①
②
解方程:例 1、(x+3)(x-1)=-7
解:原方程可变形为:
(x+2) =0
x+2=0或x+2=0
∴ x1=-2 ,x2=-2
x2+2x+4 =0
左边分解成两个一次因式 的乘积
至少有一个一次因式为零得到两个一元一次方程
两个一元一次方程的解就是原方程的解
方程右边化为零
例题讲解
简记歌决:
右化零,左分解
两因式,各求解
例2、(3x+1)2-4= 0
解:原方程可变形为
平方差公式.
例题讲解
反过来:
(x+p)(x+q)
x
x
3
-6
小结:(1).因式分解竖直写;
(2).交叉相乘验中项;
3x-6x=-3x
(3).横向写出两因式.
(x+3)和(x-6)
解:原式=
(x+3)
(x-6)
想一想:
2、把
x
x
5
3
(x+5)
(x+3)
a
a
-5
-9
解:
(a-5)(a-9)=0
a-5=o或a-9=0
5x+3x=8x
-5a-9a=-14a
例题讲解
十字相乘法
(1)x +12x=0 (2) x +2x+1 = 1;
精讲实练
用分解因式法解方程:
完全平方公式.
提公因式.
(3)x2+6x-7=0
精讲实练
-x+7x=6x
十字相乘法
1.解下列方程:解: 因式分解,得(1)x2+x=0x(x+1 ) = 0.得x= 0或x+ 1 =0,x1=0 ,x2=-1.解:因式分解,得练习1解:化为一般式为因式分解,得x2-2x+1 = 0.(x-1 )(x-1 ) = 0.有x-1 = 0或x-1 = 0,x1=x2=1.解:因式分解,得( 2x+ 11 )( 2x-11 ) = 0.有2x+ 11 = 0或2x-11= 0,12.把小圆形场地的半径增加5m得到大圆形场地,场地面积增加了一倍,求小圆形场地的半径.解:设小圆形场地的半径为r根据题意(r+ 5 )2×π=2r2π.因式分解,得于是得答:小圆形场地的半径是1
同课章节目录
