2022—2023学年人教版数学九年级上册21.2.4 一元二次方程的根与系数的关系 课件 (共17张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册21.2.4 一元二次方程的根与系数的关系 课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 740.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
21.2.4 一元二次方程的根与系数的关系
2.一元二次方程的求根公式是什么?
回顾旧知
ax2+bx+c=0(a≠0)
1.一元二次方程的一般形式是什么?
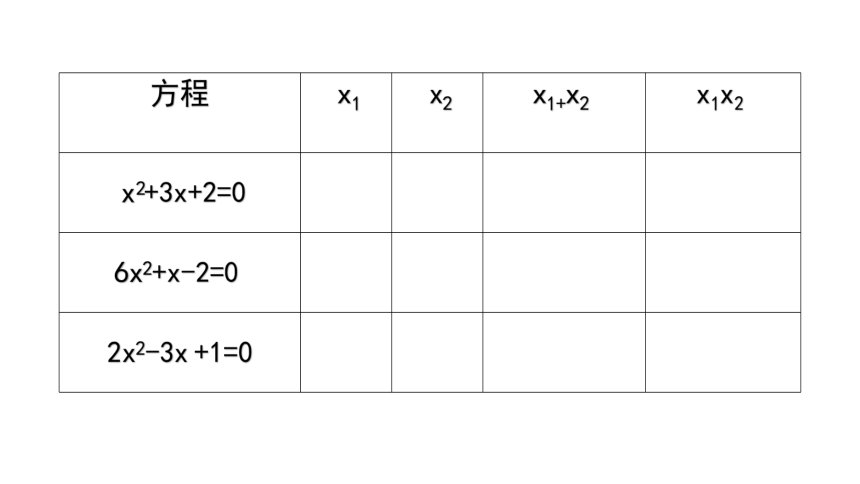
同学们,我们来做一个游戏,看谁能更快速的说出下列一元二次方程的两根和与两根积?
(1)x2+3x+2=0
(2)6x2+x-2=0
(3)2x2-3x +1=0
方程 x1 x2 x1+x2 x1x2
x2+3x+2=0
6x2+x-2=0
2x2-3x +1=0
一元二次方程ax2+bx+c=0(a≠0);
当b2-4ac≥0时有两个根:
韦达定理:
如果方程ax2+bx+c=0(a≠0)有两个实数根
那么
说出下列各方程的两根之和与两根之积:
(1)x2-2x-1=0
(3) 2x2 - 6x =0
(4) 3x2 = 4
(2) 2x2 - 3x + =0
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2= -
说一说:
例1:方程2x2-3x+1=0的两根记作x1,x2
不解方程,求下列代数式的值:
(1)
(2)
(3)
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
利用根与系数的关系求代数式的值,常用类型还有:
例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值.
解法一:
设方程的另一个根为x1
由根与系数的关系,得
2 + x2 = k+1
2 x2 = 3k
解得
x2 =-3
k =-2
答:方程的另一个根是-3,k的值是-2.
解法二:
把 x=2 代入方程,
得 4-2(k+1)+3k=0
解得 k= -2
则此方程为x2+x-6=0
(x+3)(x-2)=0
∴ x1=-3, x2=2
答:方程的另一个根是-3,k的值是-2.
例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值.
4
1
14
12
则:
=
=
试一试:
2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值.
解:
x1+x2 = - 2 , x1x2 =
∴ (x1+1)(x2+1)
= x1 x2 + (x1+x2)+1
= -2+( )+1
=
∵
1. 已知一元二次方程2x2+mx+3=0的一个根是1,则另一个根是______
练
练
一
解:
设方程的两个根分别是x1 , x2 ,其中x1=1 .
根据x1 . x2 = ,
即1. x2
∴ x2
应用新知
练
练
一
2. 设x1,x2为方程x2-2x-1=0的两个根,求下列各式的值:
(1)x1+x2 = , (2) x1 x2 = ,
(3) = , (4) = .
a = 1 , b = -2 , c = -1.
解:
∴ x1+x2=
=2 ,
∴ x12 + x22 = (x1 + x2)2 - 2x1 x2
∵ (x1 + x2)2 =x12 + 2x1 x2 + x22
x1 x2=
=-1.
=-2 .
2
-1
-2
6
应用新知
= 22 - 2×(-1)= 6
一元二次方程的根与系数的关系:
如果一元二次方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,
那么x1+x2= , x1 x2=
(韦达定理)
常数项
一次项系数
二次项系数
注意系数符号。
归纳小结
21.2.4 一元二次方程的根与系数的关系
2.一元二次方程的求根公式是什么?
回顾旧知
ax2+bx+c=0(a≠0)
1.一元二次方程的一般形式是什么?
同学们,我们来做一个游戏,看谁能更快速的说出下列一元二次方程的两根和与两根积?
(1)x2+3x+2=0
(2)6x2+x-2=0
(3)2x2-3x +1=0
方程 x1 x2 x1+x2 x1x2
x2+3x+2=0
6x2+x-2=0
2x2-3x +1=0
一元二次方程ax2+bx+c=0(a≠0);
当b2-4ac≥0时有两个根:
韦达定理:
如果方程ax2+bx+c=0(a≠0)有两个实数根
那么
说出下列各方程的两根之和与两根之积:
(1)x2-2x-1=0
(3) 2x2 - 6x =0
(4) 3x2 = 4
(2) 2x2 - 3x + =0
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2= -
说一说:
例1:方程2x2-3x+1=0的两根记作x1,x2
不解方程,求下列代数式的值:
(1)
(2)
(3)
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
利用根与系数的关系求代数式的值,常用类型还有:
例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值.
解法一:
设方程的另一个根为x1
由根与系数的关系,得
2 + x2 = k+1
2 x2 = 3k
解得
x2 =-3
k =-2
答:方程的另一个根是-3,k的值是-2.
解法二:
把 x=2 代入方程,
得 4-2(k+1)+3k=0
解得 k= -2
则此方程为x2+x-6=0
(x+3)(x-2)=0
∴ x1=-3, x2=2
答:方程的另一个根是-3,k的值是-2.
例2、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值.
4
1
14
12
则:
=
=
试一试:
2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值.
解:
x1+x2 = - 2 , x1x2 =
∴ (x1+1)(x2+1)
= x1 x2 + (x1+x2)+1
= -2+( )+1
=
∵
1. 已知一元二次方程2x2+mx+3=0的一个根是1,则另一个根是______
练
练
一
解:
设方程的两个根分别是x1 , x2 ,其中x1=1 .
根据x1 . x2 = ,
即1. x2
∴ x2
应用新知
练
练
一
2. 设x1,x2为方程x2-2x-1=0的两个根,求下列各式的值:
(1)x1+x2 = , (2) x1 x2 = ,
(3) = , (4) = .
a = 1 , b = -2 , c = -1.
解:
∴ x1+x2=
=2 ,
∴ x12 + x22 = (x1 + x2)2 - 2x1 x2
∵ (x1 + x2)2 =x12 + 2x1 x2 + x22
x1 x2=
=-1.
=-2 .
2
-1
-2
6
应用新知
= 22 - 2×(-1)= 6
一元二次方程的根与系数的关系:
如果一元二次方程ax2+bx+c=0(a≠0)的两个根是x1 , x2 ,
那么x1+x2= , x1 x2=
(韦达定理)
常数项
一次项系数
二次项系数
注意系数符号。
归纳小结
同课章节目录
