2022—2023学年人教版数学九年级上册22.1.1 二次函数 课件 (共15张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册22.1.1 二次函数 课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 755.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 21:18:40 | ||
图片预览






文档简介
(共15张PPT)
22.1.1 二次函数
1、什么是函数?
2、你学过哪些函数?这些函数的一般表达式?
课前准备:
3、下列函数关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-2x-4 (2)
(3) (4) y=8x
1.如图,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为彩色瓷砖,其余部分全为白色瓷砖,设纵向每排有n块瓷砖.
(1)设彩色瓷砖的总数为y块.
①用含n的代数式表示y,则y=________.
②y与n具有怎样的函数关系?
(2)设白色瓷砖的总数为z块.
①用含n的代数式表示z,则z=________.
②z是n的函数吗?说说理由.
自主学习:
4n+6
一次函数关系
n2+n-6
z是n的函数,因为满足函数的条件。
2.某企业今年第一季度的产值为80万元,预计产值的季平均增长率为x.
(1)设第二季度的产值为y万元,则y=__________.
设第三季度的产值为z万元,则z=____________.
(2)y,z都是x的函数吗?它们的表达式有什么不同?
80x+80
80x2+160x+80
y,z是x的函数,在函数y=80X+80中,自变量x是一次的,在函数z=80x2+160x+80中,自变量x的最高次数是二次的。
新知探究:
在自主探究中,我们得到了z=n2+n-6,z=80x2+160x+80,
这两个函数解析式,它们具有哪些共同的特征
(1)都具有y=ax +bx+c 的形式.
(2)自变量的最高次数是二次,
(3)二次项系数不等于零。
二次函数定义:一般地,如果两个变量x和y之间的函数关系可以表示成y=ax2+bx+c(a,b,c是常数,且a≠0),那么称y为x为二次函数。
结论:
其中,a叫做二次项系数,
b叫做一次项系数,
c叫做常数项.
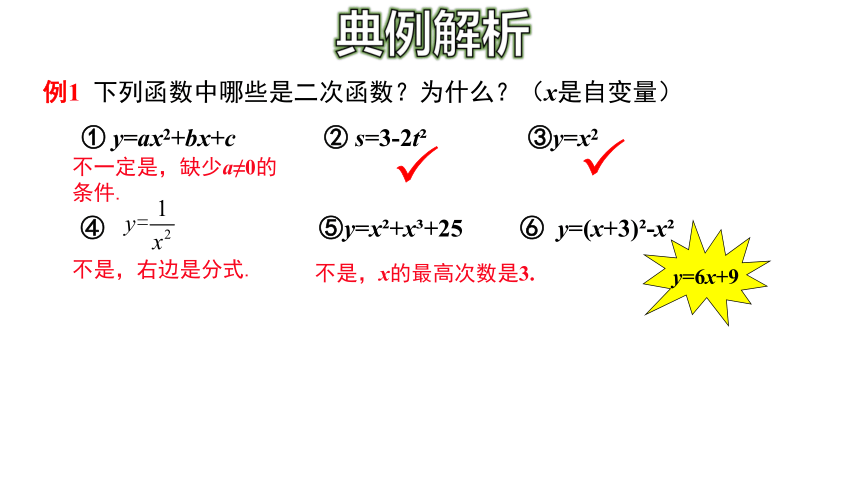
例1 下列函数中哪些是二次函数?为什么?(x是自变量)
① y=ax2+bx+c ② s=3-2t ③y=x2
④ ⑤y=x +x +25 ⑥ y=(x+3) -x
不一定是,缺少a≠0的条件.
不是,右边是分式.
不是,x的最高次数是3.
y=6x+9
典例解析
思考:二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
联系:(1)等式一边都是ax2+bx+c且a ≠0;
(2)方程ax2+bx+c=0可以看成是函数y= ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0.
知识精讲
例2 函数
(1)m取什么值时,此函数是正比例函数?
(2) m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
典例解析
1.已知: ,k取什么值时,y是x的二次函数?
解:当 =2且k+2≠0,即k=-2时, y是x的二次函数.
解:
由题意得:
∴m≠±3
2.若函数 是二次函数,那么m的取值范围是什么?
3.若函数 是二次函数,那么m的取值范围是什么?
解:
由题意得:
针对练习
例3 某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
典例解析
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
解:由题意可得 -10x2+180x+400=1120,
整理得 x2-18x+72=0,
解得 x1=6,x2=12(舍去).
所以,该产品的质量档次为第6档.
典例解析
根据实际问题列二次函数解析式
根据实际问题建立函数解析式的步骤:
(1)仔细审题,设出适当的自变量;
(2)找出等量关系,列出函数解析式;
(3)根据问题的要求,作适当的变形;
(4)根据实际要求,写出自变量的取值范围(在较为复杂且没有要求的情况下,也可不必写出).
1 (乐平市期末)长方形的周长为24 cm,其中一边长为x cm(其中x>0),面积为y cm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=12-x2
C.y=(12-x)·x D.y=2(12-x)
解析:先表示出长方形的另一边长,再利用长方形的面积公式表示出函数解析式.∵长方形的周长为24 cm,其中一边长为x cm(其中x>0),∴长方形的另一边长为12-x(cm).
∴y=(12-x)·x.
答案:C
巩固练习
2 若 y= (m2+m) -x+3是关于x的二次函数,则( )
A.m=-1或m=3
B.m≠-1且m≠0
C.m=-1
D.m=3
解析:利用二次函数的定义得出(m2+m) 是二次项,可得该项系数不为0,次数为2,进而可求m的值.
∵y=(m2+m) -x+3是关于x的二次函数,∴m2+m≠0,且m2-2m-1=2,由m2-2m-1=2解得m=-1或m=3,又由m2+m≠0解得m≠0且m≠-1,故m=3.
答案:D
22.1.1 二次函数
1、什么是函数?
2、你学过哪些函数?这些函数的一般表达式?
课前准备:
3、下列函数关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-2x-4 (2)
(3) (4) y=8x
1.如图,用规格相同的正方形瓷砖铺成矩形地面,其中,横向瓷砖比纵向瓷砖每排多5块,矩形地面最外面一圈为彩色瓷砖,其余部分全为白色瓷砖,设纵向每排有n块瓷砖.
(1)设彩色瓷砖的总数为y块.
①用含n的代数式表示y,则y=________.
②y与n具有怎样的函数关系?
(2)设白色瓷砖的总数为z块.
①用含n的代数式表示z,则z=________.
②z是n的函数吗?说说理由.
自主学习:
4n+6
一次函数关系
n2+n-6
z是n的函数,因为满足函数的条件。
2.某企业今年第一季度的产值为80万元,预计产值的季平均增长率为x.
(1)设第二季度的产值为y万元,则y=__________.
设第三季度的产值为z万元,则z=____________.
(2)y,z都是x的函数吗?它们的表达式有什么不同?
80x+80
80x2+160x+80
y,z是x的函数,在函数y=80X+80中,自变量x是一次的,在函数z=80x2+160x+80中,自变量x的最高次数是二次的。
新知探究:
在自主探究中,我们得到了z=n2+n-6,z=80x2+160x+80,
这两个函数解析式,它们具有哪些共同的特征
(1)都具有y=ax +bx+c 的形式.
(2)自变量的最高次数是二次,
(3)二次项系数不等于零。
二次函数定义:一般地,如果两个变量x和y之间的函数关系可以表示成y=ax2+bx+c(a,b,c是常数,且a≠0),那么称y为x为二次函数。
结论:
其中,a叫做二次项系数,
b叫做一次项系数,
c叫做常数项.
例1 下列函数中哪些是二次函数?为什么?(x是自变量)
① y=ax2+bx+c ② s=3-2t ③y=x2
④ ⑤y=x +x +25 ⑥ y=(x+3) -x
不一定是,缺少a≠0的条件.
不是,右边是分式.
不是,x的最高次数是3.
y=6x+9
典例解析
思考:二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
联系:(1)等式一边都是ax2+bx+c且a ≠0;
(2)方程ax2+bx+c=0可以看成是函数y= ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0.
知识精讲
例2 函数
(1)m取什么值时,此函数是正比例函数?
(2) m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
典例解析
1.已知: ,k取什么值时,y是x的二次函数?
解:当 =2且k+2≠0,即k=-2时, y是x的二次函数.
解:
由题意得:
∴m≠±3
2.若函数 是二次函数,那么m的取值范围是什么?
3.若函数 是二次函数,那么m的取值范围是什么?
解:
由题意得:
针对练习
例3 某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
典例解析
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
解:由题意可得 -10x2+180x+400=1120,
整理得 x2-18x+72=0,
解得 x1=6,x2=12(舍去).
所以,该产品的质量档次为第6档.
典例解析
根据实际问题列二次函数解析式
根据实际问题建立函数解析式的步骤:
(1)仔细审题,设出适当的自变量;
(2)找出等量关系,列出函数解析式;
(3)根据问题的要求,作适当的变形;
(4)根据实际要求,写出自变量的取值范围(在较为复杂且没有要求的情况下,也可不必写出).
1 (乐平市期末)长方形的周长为24 cm,其中一边长为x cm(其中x>0),面积为y cm2,则这样的长方形中y与x的关系可以写为( )
A.y=x2 B.y=12-x2
C.y=(12-x)·x D.y=2(12-x)
解析:先表示出长方形的另一边长,再利用长方形的面积公式表示出函数解析式.∵长方形的周长为24 cm,其中一边长为x cm(其中x>0),∴长方形的另一边长为12-x(cm).
∴y=(12-x)·x.
答案:C
巩固练习
2 若 y= (m2+m) -x+3是关于x的二次函数,则( )
A.m=-1或m=3
B.m≠-1且m≠0
C.m=-1
D.m=3
解析:利用二次函数的定义得出(m2+m) 是二次项,可得该项系数不为0,次数为2,进而可求m的值.
∵y=(m2+m) -x+3是关于x的二次函数,∴m2+m≠0,且m2-2m-1=2,由m2-2m-1=2解得m=-1或m=3,又由m2+m≠0解得m≠0且m≠-1,故m=3.
答案:D
同课章节目录
