2022—2023学年沪科版数学七年级上册3.1 一元一次方程及其解法(第1课时)课件(共22张PPT)
文档属性
| 名称 | 2022—2023学年沪科版数学七年级上册3.1 一元一次方程及其解法(第1课时)课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 860.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 21:26:09 | ||
图片预览







文档简介
(共22张PPT)
3.1一元一次方程及
其解法(第1课时)
方程定义:
含有未知数的等式叫方程。
①
②
(三)引入新知:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
(2)某校女生占全体学生的52%,比男生多80人,问这个学校有多少学生?
(3)学校计划购进一批教学设备,若购买6台计算机和8台投影仪一共要用28800元,已知计算机每台3200元,求投影仪每台多少元?
(1)4x=24 (2)0.52x-(1-0.52)x=80 (3)6x3200+8x=28800
观察以上的三个方程,每个方程有几个未知数,未知数的指数是多少?
一元一次方程
只含有一个未知数(元),未知数的次数都是1,且等式两边都是整式的方程叫做一元一次方程
判断下列各式是不是一元一次方程?
牛刀小试
① x+3y=4
② 2x- =6
③ -6x=0
④
⑤8-2=6
⑥2y+8=2y+3x
×
√
×
×
√
×
当x 等于多少时,下列方程成立?
(1)4x=24 (2) 170-150x=20
(1)当x=6时,等号左右两边相等,x=6叫做方程4x=24的解
(2)当x=1时,等号左右两边相等,x=1叫做方程170-150x=20的解
使方程左右两边相等的未知数的值
一元方程的解也叫做方程的根.
解方程就是求方程的解的过程
叫做方程的解.
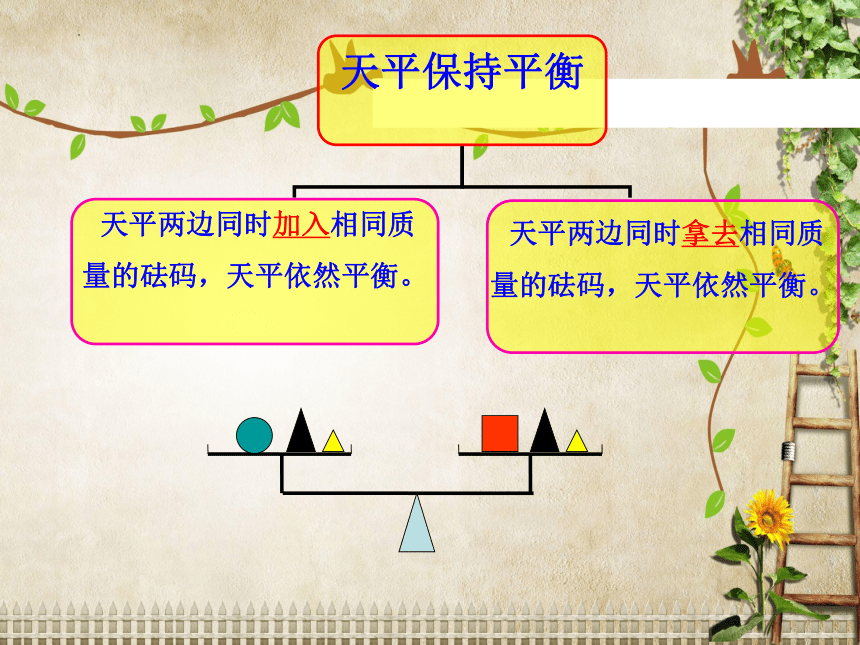
天平保持平衡
天平两边同时加入相同质
量的砝码,天平依然平衡。
天平两边同时拿去相同质
量的砝码,天平依然平衡。
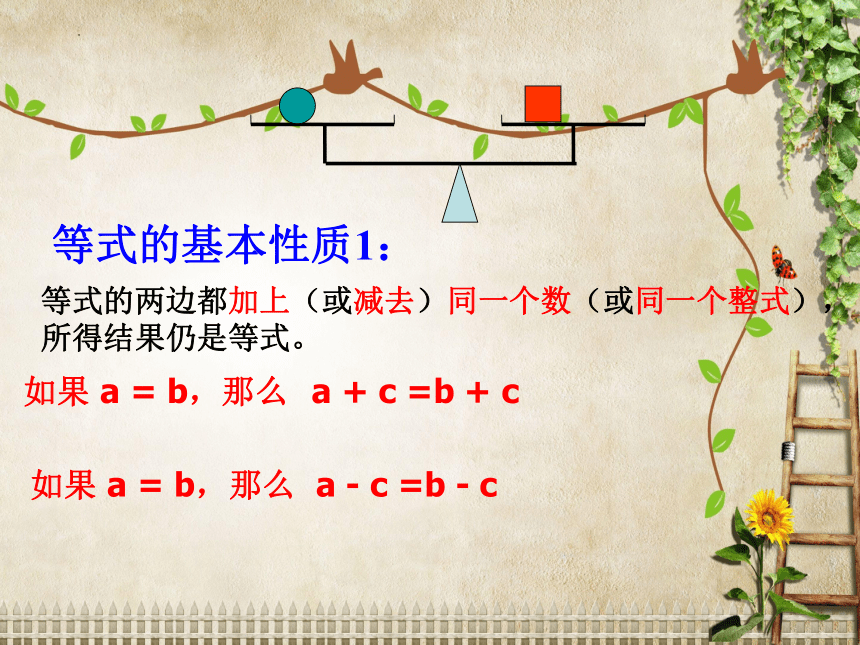
等式的基本性质1:
如果 a = b,那么
等式的两边都加上(或减去)同一个数(或同一个整式),所得结果仍是等式。
a + c =b + c
a - c =b - c
如果 a = b,那么
天平保持平衡
天平两边同时扩大到原来相
同的倍数,天平依然平衡。
天平两边同时缩小到原来的
几分之几,天平依然平衡。
等式的基本性质2:
如果 a = b,
等式的两边都乘以(或除以)同一个数,(除数不能为0),所得结果仍是等式。
如果 a = b,且c≠0,
那么 a c = b c
那么
a/c=b/c
脚踏实地
1.说明下列变形是根据等式哪一条基本性质得到的
(1)如果5x+3=7,那么5x=4
(2)如果-8x=4,那么x=-0.5
(3)如果-5a=-5b,那么a=b
(4)如果3x=2x+1,那么x=1
等式基本性质1,两边同减去3
等式基本性质1 ,两边同减去2x
等式基本性质2 ,两边同除以-5
等式基本性质2 ,两边同除以-8
例1.解方程:
2x-4=18
解: 方程两边同时加上4,得
2x-4+4=18 +4
即 2x=22
两边都除以2,得
x=11
检验:把x=11分别代入原方程的两边,得
左边=2×11-4=18,
右边=18,
即 左边=右边.
所以 x=11是原方程的解.
(等式基本性质1)
(等式基本性质2)
知识回顾
这个方程的变换过程是应用哪条性质的? 3 = 2x + 1
(性质1)
(性质2)
(性质3)
3–1 = 2x + 1–1
2 = 2x
1 = x
x = 1
解方程:(1)5x–3 = 7 ,(2)3x = x + 1
3 = 2x
+1
3 = 2x
-1
+1-1
5x = 7
-3
5x = 7
+3
-3+3
3x = + 1
x
3x = + 1
-x
x -x
观察思考
你能发现其中的共同点么?
把方程中的某一项改变符号后,从方程的
一边移到另一边,这种变形叫做“移项”
小试牛刀
1、解下列方程,并口算检验
2、解下列方程,口算检验
(1) 2x = x + 5 (2) 3x+20=4x-25
2、根据等式的基本性质解下列方程.
(1) 2x-9=5x
(2)
大显神通
解:
合并同类项,得
两边同除以
,得
(等式的基本性质2)
归纳总结:
这节课你有什么收获?
2、解一元一次方程的实质就是:
——利用等式的性质求出未知数的值。
——将方程化为“x=a (a为常数)”的形式。
1、等式的基本性质;
① 如果 a = b,那么 a ± c = b ± c
② 如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
练习巩固
1.下列运用等式性质进行变形,不正确的是( )
A.如果a=b,那么a-c=b-c B.如果a=b,那么2a=a+b
C.如果a=b,那么 D.如果 ,那么a=b
2.已知5a+8b=3b+10,试用等式性质求a+b的值
3.若关于 的方程 是一元一次方程,求这个方程的解。
D
作业:
1.课本P83 习题3.1 1, 2.
2.练习册(P47-48)
谢谢
3.1一元一次方程及
其解法(第1课时)
方程定义:
含有未知数的等式叫方程。
①
②
(三)引入新知:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
(2)某校女生占全体学生的52%,比男生多80人,问这个学校有多少学生?
(3)学校计划购进一批教学设备,若购买6台计算机和8台投影仪一共要用28800元,已知计算机每台3200元,求投影仪每台多少元?
(1)4x=24 (2)0.52x-(1-0.52)x=80 (3)6x3200+8x=28800
观察以上的三个方程,每个方程有几个未知数,未知数的指数是多少?
一元一次方程
只含有一个未知数(元),未知数的次数都是1,且等式两边都是整式的方程叫做一元一次方程
判断下列各式是不是一元一次方程?
牛刀小试
① x+3y=4
② 2x- =6
③ -6x=0
④
⑤8-2=6
⑥2y+8=2y+3x
×
√
×
×
√
×
当x 等于多少时,下列方程成立?
(1)4x=24 (2) 170-150x=20
(1)当x=6时,等号左右两边相等,x=6叫做方程4x=24的解
(2)当x=1时,等号左右两边相等,x=1叫做方程170-150x=20的解
使方程左右两边相等的未知数的值
一元方程的解也叫做方程的根.
解方程就是求方程的解的过程
叫做方程的解.
天平保持平衡
天平两边同时加入相同质
量的砝码,天平依然平衡。
天平两边同时拿去相同质
量的砝码,天平依然平衡。
等式的基本性质1:
如果 a = b,那么
等式的两边都加上(或减去)同一个数(或同一个整式),所得结果仍是等式。
a + c =b + c
a - c =b - c
如果 a = b,那么
天平保持平衡
天平两边同时扩大到原来相
同的倍数,天平依然平衡。
天平两边同时缩小到原来的
几分之几,天平依然平衡。
等式的基本性质2:
如果 a = b,
等式的两边都乘以(或除以)同一个数,(除数不能为0),所得结果仍是等式。
如果 a = b,且c≠0,
那么 a c = b c
那么
a/c=b/c
脚踏实地
1.说明下列变形是根据等式哪一条基本性质得到的
(1)如果5x+3=7,那么5x=4
(2)如果-8x=4,那么x=-0.5
(3)如果-5a=-5b,那么a=b
(4)如果3x=2x+1,那么x=1
等式基本性质1,两边同减去3
等式基本性质1 ,两边同减去2x
等式基本性质2 ,两边同除以-5
等式基本性质2 ,两边同除以-8
例1.解方程:
2x-4=18
解: 方程两边同时加上4,得
2x-4+4=18 +4
即 2x=22
两边都除以2,得
x=11
检验:把x=11分别代入原方程的两边,得
左边=2×11-4=18,
右边=18,
即 左边=右边.
所以 x=11是原方程的解.
(等式基本性质1)
(等式基本性质2)
知识回顾
这个方程的变换过程是应用哪条性质的? 3 = 2x + 1
(性质1)
(性质2)
(性质3)
3–1 = 2x + 1–1
2 = 2x
1 = x
x = 1
解方程:(1)5x–3 = 7 ,(2)3x = x + 1
3 = 2x
+1
3 = 2x
-1
+1-1
5x = 7
-3
5x = 7
+3
-3+3
3x = + 1
x
3x = + 1
-x
x -x
观察思考
你能发现其中的共同点么?
把方程中的某一项改变符号后,从方程的
一边移到另一边,这种变形叫做“移项”
小试牛刀
1、解下列方程,并口算检验
2、解下列方程,口算检验
(1) 2x = x + 5 (2) 3x+20=4x-25
2、根据等式的基本性质解下列方程.
(1) 2x-9=5x
(2)
大显神通
解:
合并同类项,得
两边同除以
,得
(等式的基本性质2)
归纳总结:
这节课你有什么收获?
2、解一元一次方程的实质就是:
——利用等式的性质求出未知数的值。
——将方程化为“x=a (a为常数)”的形式。
1、等式的基本性质;
① 如果 a = b,那么 a ± c = b ± c
② 如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
练习巩固
1.下列运用等式性质进行变形,不正确的是( )
A.如果a=b,那么a-c=b-c B.如果a=b,那么2a=a+b
C.如果a=b,那么 D.如果 ,那么a=b
2.已知5a+8b=3b+10,试用等式性质求a+b的值
3.若关于 的方程 是一元一次方程,求这个方程的解。
D
作业:
1.课本P83 习题3.1 1, 2.
2.练习册(P47-48)
谢谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
