3.3.2 抛物线的简单几何性质 教案
文档属性
| 名称 | 3.3.2 抛物线的简单几何性质 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 402.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 13:47:53 | ||
图片预览

文档简介
第三章 圆锥曲线的方程
3.3.2 抛物线的简单几何性质
教学设计
一、教学目标
1.掌握抛物线的简单几何性质,能利用简单性质求抛物线方程.
2.理解抛物线简单几何性质的推导过程,体会数形结合的思想.
3.能用抛物线的简单几何性质分析解决一些简单的问题.
二、教学重难点
1、教学重点
抛物线的几何性质.
2、教学难点
抛物线的几何性质及其应用.
三、教学过程
1、新课导入
前面我们已经学习了椭圆与双曲线,根据它们的标准方程,得到了椭圆与双曲线的简单几何性质. 在上节课,我们已经学习了抛物线的定义和标准方程,那么类比用方程研究椭圆、双曲线几何性质的过程与方法,本节课就根据标准方程来探索抛物线的几何性质.
2、探索新知
1.范围
因为,由方程可知,对于抛物线上的点,,,当时,抛物线在y轴的右侧,开口方向与x轴的正方向相同;当x的值增大时,的值也增大,这说明抛物线向右上方和右下方无限延伸.
2.对称性
以代y,方程不变,所以抛物线关于x轴对称. 抛物线的对称轴叫做抛物线的轴.
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点. 在方程中,当时,,因此抛物线的顶点就是原点.
4.离心率
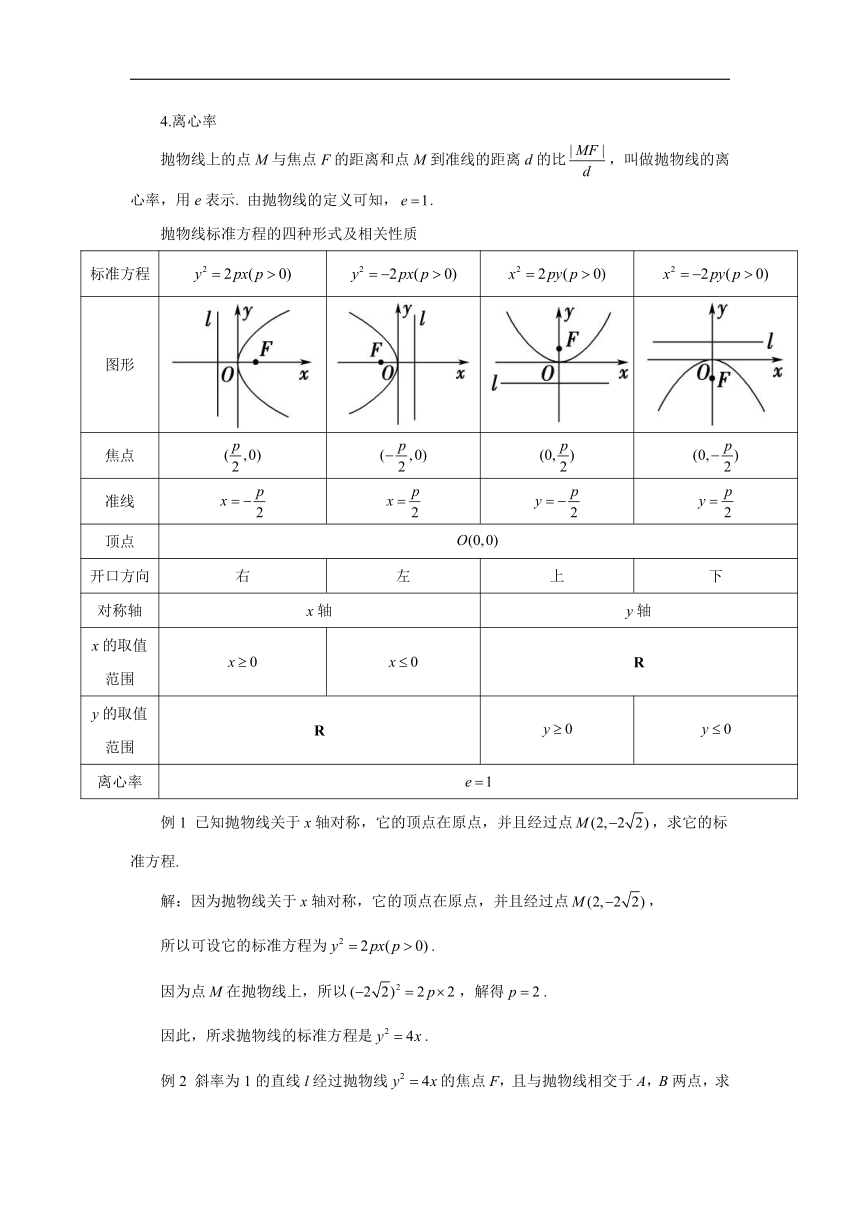
抛物线上的点M与焦点F的距离和点M到准线的距离d的比,叫做抛物线的离心率,用e表示. 由抛物线的定义可知,.
抛物线标准方程的四种形式及相关性质
标准方程
图形
焦点
准线
顶点
开口方向 右 左 上 下
对称轴 x轴 y轴
x的取值范围 R
y的取值范围 R
离心率
例1 已知抛物线关于x轴对称,它的顶点在原点,并且经过点,求它的标准方程.
解:因为抛物线关于x轴对称,它的顶点在原点,并且经过点,
所以可设它的标准方程为.
因为点M在抛物线上,所以,解得.
因此,所求抛物线的标准方程是.
例2 斜率为1的直线l经过抛物线的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
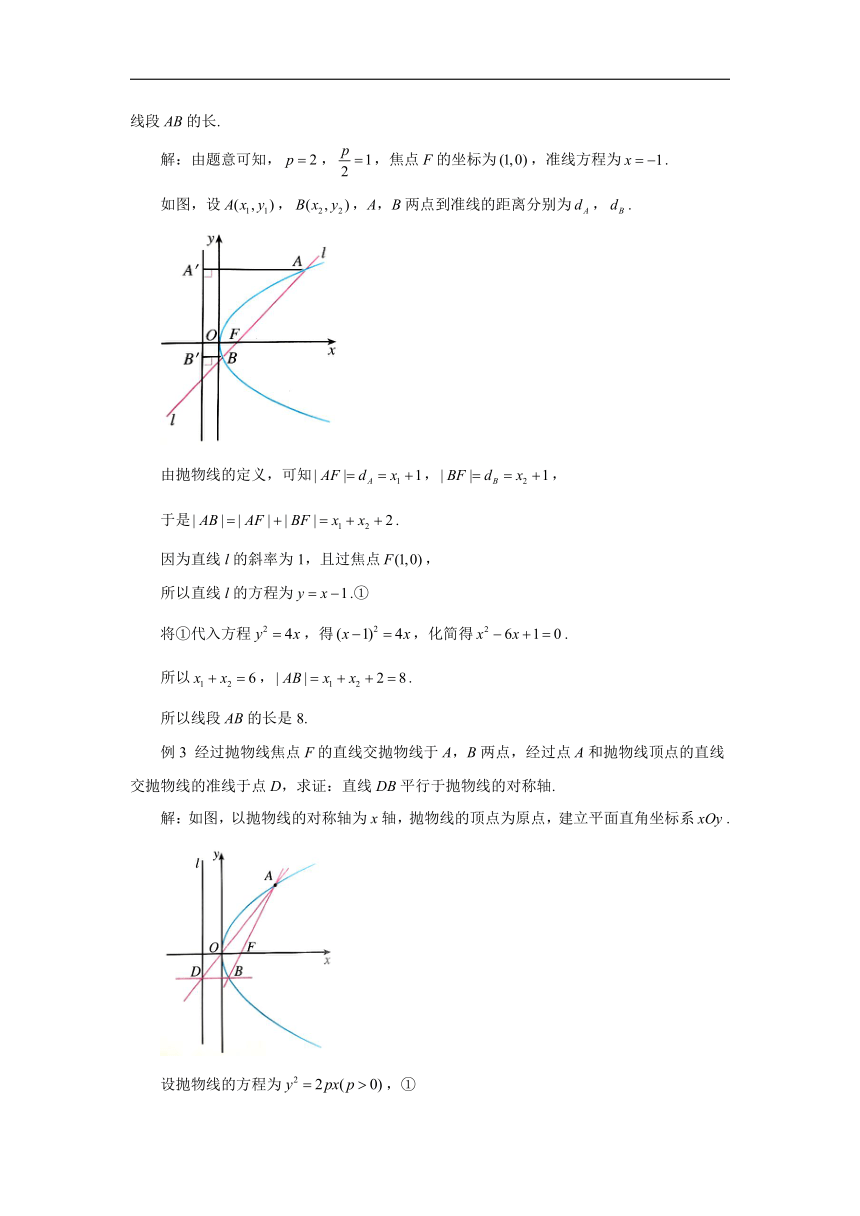
解:由题意可知,,,焦点F的坐标为,准线方程为.
如图,设,,A,B两点到准线的距离分别为,.
由抛物线的定义,可知,,
于是.
因为直线l的斜率为1,且过焦点,
所以直线l的方程为.①
将①代入方程,得,化简得.
所以,.
所以线段AB的长是8.
例3 经过抛物线焦点F的直线交抛物线于A,B两点,经过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
解:如图,以抛物线的对称轴为x轴,抛物线的顶点为原点,建立平面直角坐标系.
设抛物线的方程为,①
点A的坐标为,则直线OA的方程为,②
抛物线的准线方程是.③
联立②③,可得点D的纵坐标为.
因为焦点F的坐标是,当时,直线AF的方程为.④
联立①④,消去x,可得,即,
可得点B的纵坐标为,与点D的纵坐标相等,于是DB平行于x轴.
当时,易知结论成立.
所以,直线DB平行于抛物线的对称轴.
例4 如图,已知定点,轴于点C,M是线段OB上任意一点,轴于点,于点E,OE与MD相交于点,求点的轨迹方程.
解:设点,,其中,则点的坐标为.
由题意,直线OB的方程为,①
因为点在OB上,将点的坐标代入①,得,②
所以点的横坐标满足②.
直线OE的方程为,③
因为点在OE上,所以点的坐标满足③.
将②代入③,消去,得,即点的轨迹方程.
3、课堂练习
1.已知抛物线的对称轴为x轴,顶点在原点,焦点在直线上,则此抛物线的标准方程是( )
A. B. C. D.
答案:C
解析:在方程中,令,得,抛物线的焦点为,抛物线的标准方程是,故选C.
2.抛物线上一点P到焦点的距离为3,则点P到y轴的距离为( )
A. B.1 C.2 D.3
答案:A
解析:根据抛物线方程可求得焦点坐标为,准线方程为.根据抛物线定义,得,解得,代入抛物线方程可得,点P到y轴的距离为.故选A.
3.直线与抛物线交于A,B两点,过A,B两点向抛物线的准线作垂线,垂足分别为P,Q,则梯形的面积为_______________.
答案:48
解析:由,消去y得,得或9,即或,所以,或,,,所以梯形的面积.
4.已知焦点为F的抛物线上有一点,若以A为圆心,为半径的圆A被y轴截得的弦长为,则_______________.
答案:2
解析:点在抛物线上,,,
抛物线的焦点,即.由抛物线定义知,
即圆A的半径,点A到y轴的距离,,
即,解得(舍去).
4、小结作业
小结:本节课学习了抛物线的简单几何性质及其应用.
作业:完成本节课课后习题.
四、板书设计
3.3.2 抛物线的简单几何性质
1.范围:因为,由方程可知,对于抛物线上的点,,,当时,抛物线在y轴的右侧,开口方向与x轴的正方向相同;当x的值增大时,的值也增大,这说明抛物线向右上方和右下方无限延伸.
2.对称性:以代y,方程不变,所以抛物线关于x轴对称. 抛物线的对称轴叫做抛物线的轴.
3.顶点:抛物线和它的轴的交点叫做抛物线的顶点. 在方程中,当时,,因此抛物线的顶点就是原点.
4.离心率:抛物线上的点M与焦点F的距离和点M到准线的距离d的比,叫做抛物线的离心率,用e表示. 由抛物线的定义可知,.
3.3.2 抛物线的简单几何性质
教学设计
一、教学目标
1.掌握抛物线的简单几何性质,能利用简单性质求抛物线方程.
2.理解抛物线简单几何性质的推导过程,体会数形结合的思想.
3.能用抛物线的简单几何性质分析解决一些简单的问题.
二、教学重难点
1、教学重点
抛物线的几何性质.
2、教学难点
抛物线的几何性质及其应用.
三、教学过程
1、新课导入
前面我们已经学习了椭圆与双曲线,根据它们的标准方程,得到了椭圆与双曲线的简单几何性质. 在上节课,我们已经学习了抛物线的定义和标准方程,那么类比用方程研究椭圆、双曲线几何性质的过程与方法,本节课就根据标准方程来探索抛物线的几何性质.
2、探索新知
1.范围
因为,由方程可知,对于抛物线上的点,,,当时,抛物线在y轴的右侧,开口方向与x轴的正方向相同;当x的值增大时,的值也增大,这说明抛物线向右上方和右下方无限延伸.
2.对称性
以代y,方程不变,所以抛物线关于x轴对称. 抛物线的对称轴叫做抛物线的轴.
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点. 在方程中,当时,,因此抛物线的顶点就是原点.
4.离心率
抛物线上的点M与焦点F的距离和点M到准线的距离d的比,叫做抛物线的离心率,用e表示. 由抛物线的定义可知,.
抛物线标准方程的四种形式及相关性质
标准方程
图形
焦点
准线
顶点
开口方向 右 左 上 下
对称轴 x轴 y轴
x的取值范围 R
y的取值范围 R
离心率
例1 已知抛物线关于x轴对称,它的顶点在原点,并且经过点,求它的标准方程.
解:因为抛物线关于x轴对称,它的顶点在原点,并且经过点,
所以可设它的标准方程为.
因为点M在抛物线上,所以,解得.
因此,所求抛物线的标准方程是.
例2 斜率为1的直线l经过抛物线的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
解:由题意可知,,,焦点F的坐标为,准线方程为.
如图,设,,A,B两点到准线的距离分别为,.
由抛物线的定义,可知,,
于是.
因为直线l的斜率为1,且过焦点,
所以直线l的方程为.①
将①代入方程,得,化简得.
所以,.
所以线段AB的长是8.
例3 经过抛物线焦点F的直线交抛物线于A,B两点,经过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
解:如图,以抛物线的对称轴为x轴,抛物线的顶点为原点,建立平面直角坐标系.
设抛物线的方程为,①
点A的坐标为,则直线OA的方程为,②
抛物线的准线方程是.③
联立②③,可得点D的纵坐标为.
因为焦点F的坐标是,当时,直线AF的方程为.④
联立①④,消去x,可得,即,
可得点B的纵坐标为,与点D的纵坐标相等,于是DB平行于x轴.
当时,易知结论成立.
所以,直线DB平行于抛物线的对称轴.
例4 如图,已知定点,轴于点C,M是线段OB上任意一点,轴于点,于点E,OE与MD相交于点,求点的轨迹方程.
解:设点,,其中,则点的坐标为.
由题意,直线OB的方程为,①
因为点在OB上,将点的坐标代入①,得,②
所以点的横坐标满足②.
直线OE的方程为,③
因为点在OE上,所以点的坐标满足③.
将②代入③,消去,得,即点的轨迹方程.
3、课堂练习
1.已知抛物线的对称轴为x轴,顶点在原点,焦点在直线上,则此抛物线的标准方程是( )
A. B. C. D.
答案:C
解析:在方程中,令,得,抛物线的焦点为,抛物线的标准方程是,故选C.
2.抛物线上一点P到焦点的距离为3,则点P到y轴的距离为( )
A. B.1 C.2 D.3
答案:A
解析:根据抛物线方程可求得焦点坐标为,准线方程为.根据抛物线定义,得,解得,代入抛物线方程可得,点P到y轴的距离为.故选A.
3.直线与抛物线交于A,B两点,过A,B两点向抛物线的准线作垂线,垂足分别为P,Q,则梯形的面积为_______________.
答案:48
解析:由,消去y得,得或9,即或,所以,或,,,所以梯形的面积.
4.已知焦点为F的抛物线上有一点,若以A为圆心,为半径的圆A被y轴截得的弦长为,则_______________.
答案:2
解析:点在抛物线上,,,
抛物线的焦点,即.由抛物线定义知,
即圆A的半径,点A到y轴的距离,,
即,解得(舍去).
4、小结作业
小结:本节课学习了抛物线的简单几何性质及其应用.
作业:完成本节课课后习题.
四、板书设计
3.3.2 抛物线的简单几何性质
1.范围:因为,由方程可知,对于抛物线上的点,,,当时,抛物线在y轴的右侧,开口方向与x轴的正方向相同;当x的值增大时,的值也增大,这说明抛物线向右上方和右下方无限延伸.
2.对称性:以代y,方程不变,所以抛物线关于x轴对称. 抛物线的对称轴叫做抛物线的轴.
3.顶点:抛物线和它的轴的交点叫做抛物线的顶点. 在方程中,当时,,因此抛物线的顶点就是原点.
4.离心率:抛物线上的点M与焦点F的距离和点M到准线的距离d的比,叫做抛物线的离心率,用e表示. 由抛物线的定义可知,.
