高中数学选择性必修第三册RJ·A--6.2 排列与组合-6.2.1 排列 6.2.2 排列数 课件(共23张ppt)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·A--6.2 排列与组合-6.2.1 排列 6.2.2 排列数 课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 00:00:00 | ||
图片预览








文档简介
第六章
6.2
排列与组合
6.2.1 排列
6.2.2 排列数
学习目标
1.理解排列、排列数的概念.
2.能利用计数原理推导排列数公式,并掌握排列数公式及其变形,能运用排列数公式熟练地进行相关计算.
3.能熟练地运用排列知识解决一些有关排列的实际问题.
4.通过实例,体验数学知识的形成与发展,学会分析问题、解决问题的方式,培养解决实际问题的能力.
核心素养:逻辑推理、数学运算、数学建模.
新知学习
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
此时,要完成的一件事是“选出2名同学参加活动,1名同学参加上午的活动,另1名同学参加下午的活动”,可以分两个步骤:
第1步,确定参加上午活动的同学,从3人中任选1人,有3种选法;
第2步,确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人中去选,有2种选法.
根据分步乘法计数原理,不同的选法种数为3×2=6.
这6种不同的选法如图所示.
如果把上面问题中被取出的对象叫做元素,那么问题可叙述为:
从3个不同的元素????,????,???? 中任意取出2个,并按一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是?????????,????????,????????,????????,????????,????????,
不同的排列方法种数为3×2=6.
?
问题1中的“顺序”是什么?
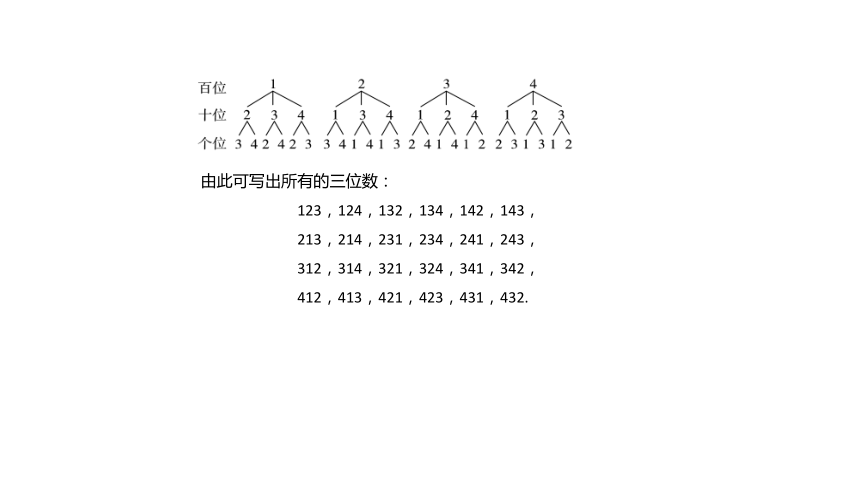
问题2?从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个
不同的三位数?
显然,从4个数字中,每次取出3个,按“百位、十位、个位”的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.可以分三个步骤来解决这个问题:
第1步,确定百位上的数字,从1,2,3,4这4个数字中任取1个,有4种方法;
第2步,确定十位上的数字,当百位上的数字确定后,十位上的数字只能从余下的3个数字中去取,有3种方法;
第3步,确定个位上的数字,当百位、十位上的数字确定后,个位的数字只能从余下的2个数字中去取,有2种方法.
根据分步乘法计数原理,从1,2,3,4这4个不同的数字中,每次取出3个数字,按“百位、十位、个位”的顺序排成一列,不同的排法种数为4×3×2=24.
因而共可得到24个不同的三位数,如图所示.
由此可写出所有的三位数:
123,124,132,134,142,143,
213,214,231,234,241,243,
312,314,321,324,341,342,
412,413,421,423,431,432.
同样,问题2可以归结为:
从4个不同的元素????,????,????,????中任意取出3个,并按照一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是
???????????????,????????????,????????????,????????????,????????????,????????????,
???????????????,????????????,????????????,????????????,????????????,????????????,
???????????????,????????????,????????????,????????????,????????????,????????????, ??
????????????,????????????,????????????,????????????,????????????,????????????.
不同的排列方法种数为4×3×2=24.
?
问题2中的“顺序”是什么?
思考:上述问题1,2的共同特点是什么?你能将它们推广到一般情形吗?
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
新知讲解
一般地,从????个不同元素中取出????(????≤????)个元素,并按照一定的顺序排成一列,叫做从????个不同元素中取出????个元素的一个排列(arrangement).
?
提示:根据排列的定义,两个排列相同的充要条件是:两个排列的元素完全相同,且元素的排列顺序也相同.例如,在问题1中,“甲乙”与“甲丙”的元素不完全相同,它们是不同的排列;“甲乙”与“乙甲”虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列.又如,在问题2中,123与134的元素不完全相同,它们是不同的排列;123与132虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列.
典例剖析
例1 某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛?
解:可以先从这6支队中选1支为主队,然后从剩下的5支队中选1支为客队.
按分步乘法计数原理,每组进行的比赛场数为6×5=30.
方法技巧:1.排列问题的判断标准:
(1)元素无重复性;
(2)元素有序性.
2.判断一个计数问题是否为排列问题的关键是看选出的元素有没有顺序要求.
例2 (1)一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
(2)学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少种不同的选法?
解:(1)可以先从这5盘菜中取1盘给同学甲,然后从剩下的4盘菜中取1盘给同学乙,最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理,不同的取法种数为5×4×3=60.
(2)可以先让同学甲从5种菜中选1种,有5种选法;再让同学乙从5种菜中选1种,也有5种选法;最后让同学丙从5种菜中选1种,同样有5种选法.按分步乘法计数原理,不同的选法种数为5×5×5=125.
新知讲解
我们把从????个不同元素中取出????(????≤????)个元素的所有不同排列的个数,叫做从????个不同元素中取出????个元素的排列数,用符号A????????表示.
?
例如,前面问题1是求从3个不同元素中取出2个元素的排列数,表示为A32.
已经算得A32=3×2=6.
问题2是求从4个不同元素中取出3个元素的排列数,表示为A43.
已经算得A43=4×3×2=24.
?
探究:从????个不同元素中取出????个元素的排列数A????????(????≤????)是多少?
?
可以先从特殊情况开始探究,例如求排列数A????2.
根据前面的求解经验,可以这样考虑:
假定有排好顺序的两个空位,如图所示,从????个不同元素中取出2个元素去填空,一个空位填上一个元素,每一种填法就得到一个排列;反之,任何一种排列总可以由这种填法得到.因此,所有不同填法的种数就是排列数A????2.
现在来计算有多少种填法.完成“填空”这件事可以分为两个步骤完成:
第1步,填第1个位置的元素,可以从这????个不同元素中任选1个,有????种选法;
第2步,填第2个位置的元素,可以从剩下的(?????1)个元素中任选1个,有(?????1)种选法.
根据分步乘法计数原理,2个空位的填法种数为A????2=????(?????1).
?
同理,求排列数A????3可以按依次填3个空位来考虑,有A????3=????(?????1)(?????2).
?
一般地,求排列数A????????可以按依次填????个空位来考虑:
假定有排好顺序的????个空位,如图所示,从????个不同元素中取出????个元素去填空,一个空位填上一个元素,每一种填法就对应一个排列.因此,所有不同填法的种数就是排列数A????????.
填空可以分为????个步骤完成:
第1步,从????个不同元素中任选1个填在第1位,有????种选法;
第2步,从剩下的(?????1)个元素中任选1个填在第2位,有(?????1)种选法;
第3步,从剩下的(?????2)个元素中任选1个填在第3位,有(?????2)种选法;
……
第m步,从剩下的[?????(?????1)]个元素中任选1个填在第????位,有(?????????+1)种选法.
根据分步乘法计数原理,????个空位的填法种数为????(?????1)(?????2)…(?????????+1).
这样,我们就得到公式
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}A????????=????(?????1)(?????2)…(?????????+1).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
这里,????,????∈?????,并且????≤????.这个公式叫做排列数公式.
?
特别地,我们把????个不同的元素全部取出的一个排列,叫做????个元素的一个全排列.
这时,排列数公式中????=????,即有
A????????=????(?????1)(?????2)×…×3×2×1.
也就是说,将????个不同的元素全部取出的排列数,等于正整数1到????的连乘积.正整数1到????的连乘积,叫做????的阶乘,用????!表示.于是,????个元素的全排列数公式可以写成
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}A????????=????!.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
另外,我们规定,0!=1.
典例剖析
例3?计算:(1)A37; (2)A47; (3)A77A44; (4)A46×A22.
解:根据排列数公式,可得
(1)A37=7×6×5=210; (2)A47=7×6×5×4=840;
(3)A77A44=7!4!=7×6×5=210; (4)A46×A22=6×5×4×3×2×1=6!=720.
?
思考:由例3可以看到,A73=A77A44=7!4!;A46×A22=6!=A66,即A64=A66A22=6!2!.
观察这两个结果,从中你发现它们的共性了吗?
?
事实上,
Amn=????(?????1)(?????2)…(?????????+1)
=?????????1?????2??????????+1?????????×?×2×1?????????×?×2×1
=A????????A??????????????????=????!?????????!.
因此,排列数公式还可以写成
?
???A????????=?????!??????????!.
提示:(1)在两个排列数公式中,????,????满足的条件都是????,????∈?????,且????≤????.
(2)公式?A????????=????!?????????!的两个作用:
一是当????,????较大时,利用科学计算器计算排列数比较方便;
二是当对含有参数的排列数的式子进行变形和论证时,写成这种形式有利于发现式子之间的关系.
(3)对于阶乘的概念,可以从两个阶乘之间的关系的角度来认识,实际上,较大数的阶乘数一定是较小数的阶乘数的整数倍.
?
例4?用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法1:如图所示,由于三位数的百位上的数字不能是0,所以可以分两步完成:
第1步,确定百位上的数字,可以从1~9这9个数字中取出1个,有A91种取法;
第2步,确定十位和个位上的数字,可以从剩下的9个数字中取出2个,有A92种取法.
根据分步乘法计数原理,所求的三位数的个数为A91×A92=9×9×8=648.
?
解法2:如图所示,符合条件的三位数可以分成三类:第1类,每一位数字都不是0的三位数,可以从1~9这9个数字中取出3个,有A93种取法;第2类,个位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和十位,有A92种取法;第3类,十位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和个位,有A92种取法.
根据分类加法计数原理,所求三位数的个数为 A93+A92+A92=9×8×7+9×8+9×8=648.
?
解法3:从0~9这10个数字中选取3个的排列数为,其中0在百位上的排列数为A92,它们的差就是用这10个数组成的没有重复数字的三位数的个数,即所求三位数的个数为
A103-A92=10×9×8-9×8=648.
?
点评:对于例4这类计数问题,从不同的角度就有不同的解题方法.
解法1根据百位数字不能是0的要求,按分步乘法计数原理完成从10个数中取出3个数组成没有重复数字的三位数这件事;
解法2是以0是否出现以及出现的位置为标准,按分类加法计数原理完成这件事;解法3是一种间接法,先求出从10个数中取出3个数的排列数,然后减去其中百位是0的排列数(不是三位数的个数),就得到没有重复数字的三位数的个数.
随堂小测
1.(1)已知A2n=56,那么????= .
(2)计算A2????????+3+A3????= .
?
8
726
2. 将4名医生与4名护士分配到四个不同单位,每个单位分配一名医生与一名护士,共有多少种不同的分配方案?
解:完成这件事可以分为两步.
第一步:把4名医生分配到四个不同的单位,等价于从4个不同元素中取出4个元素的排列问题,有A44种方法.
第二步:把4名护士分配到四个不同的单位,也有A44种方法.
根据分步乘法计数原理,不同的分配方案有A44×A44=576种.
?
3. 6本不同的书在书桌上摆成一排,要求甲、乙两本书必须放在两端,丙、丁两本书必须相邻,则不同的摆放方法有( )种.
A.24 B.36 C.48 D.60
A
4.现有5人要排成一排照相,其中甲与乙两人不相邻,且甲不站在两端,则不同的排法有 种.(用数字作答)
36
课堂小结
排列:一般地,从????个不同元素中取出????(????≤????)个元素,并按照一定的顺序排成一列,叫做从????个不同元素中取出????个元素的一个排列.
?
排列与排列数的概念:
排列数:我们把从????个不同元素中取出????(????≤????)个元素的所有不同排列的个数,叫做从????个不同元素中取出????个元素的排列数,用符号A????????表示.
?
排列数公式:
???A????????=?????!??????????!=????(?????1)(?????2)…(?????????+1)
?
A????????=????!=????(?????1)(?????2)×…×3×2×1
?
谢 谢!
6.2
排列与组合
6.2.1 排列
6.2.2 排列数
学习目标
1.理解排列、排列数的概念.
2.能利用计数原理推导排列数公式,并掌握排列数公式及其变形,能运用排列数公式熟练地进行相关计算.
3.能熟练地运用排列知识解决一些有关排列的实际问题.
4.通过实例,体验数学知识的形成与发展,学会分析问题、解决问题的方式,培养解决实际问题的能力.
核心素养:逻辑推理、数学运算、数学建模.
新知学习
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
此时,要完成的一件事是“选出2名同学参加活动,1名同学参加上午的活动,另1名同学参加下午的活动”,可以分两个步骤:
第1步,确定参加上午活动的同学,从3人中任选1人,有3种选法;
第2步,确定参加下午活动的同学,当参加上午活动的同学确定后,参加下午活动的同学只能从剩下的2人中去选,有2种选法.
根据分步乘法计数原理,不同的选法种数为3×2=6.
这6种不同的选法如图所示.
如果把上面问题中被取出的对象叫做元素,那么问题可叙述为:
从3个不同的元素????,????,???? 中任意取出2个,并按一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是?????????,????????,????????,????????,????????,????????,
不同的排列方法种数为3×2=6.
?
问题1中的“顺序”是什么?
问题2?从1,2,3,4这4个数字中,每次取出3个排成一个三位数,共可得到多少个
不同的三位数?
显然,从4个数字中,每次取出3个,按“百位、十位、个位”的顺序排成一列,就得到一个三位数.因此有多少种不同的排列方法就有多少个不同的三位数.可以分三个步骤来解决这个问题:
第1步,确定百位上的数字,从1,2,3,4这4个数字中任取1个,有4种方法;
第2步,确定十位上的数字,当百位上的数字确定后,十位上的数字只能从余下的3个数字中去取,有3种方法;
第3步,确定个位上的数字,当百位、十位上的数字确定后,个位的数字只能从余下的2个数字中去取,有2种方法.
根据分步乘法计数原理,从1,2,3,4这4个不同的数字中,每次取出3个数字,按“百位、十位、个位”的顺序排成一列,不同的排法种数为4×3×2=24.
因而共可得到24个不同的三位数,如图所示.
由此可写出所有的三位数:
123,124,132,134,142,143,
213,214,231,234,241,243,
312,314,321,324,341,342,
412,413,421,423,431,432.
同样,问题2可以归结为:
从4个不同的元素????,????,????,????中任意取出3个,并按照一定的顺序排成一列,共有多少种不同的排列方法?
所有不同的排列是
???????????????,????????????,????????????,????????????,????????????,????????????,
???????????????,????????????,????????????,????????????,????????????,????????????,
???????????????,????????????,????????????,????????????,????????????,????????????, ??
????????????,????????????,????????????,????????????,????????????,????????????.
不同的排列方法种数为4×3×2=24.
?
问题2中的“顺序”是什么?
思考:上述问题1,2的共同特点是什么?你能将它们推广到一般情形吗?
问题1和问题2都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
新知讲解
一般地,从????个不同元素中取出????(????≤????)个元素,并按照一定的顺序排成一列,叫做从????个不同元素中取出????个元素的一个排列(arrangement).
?
提示:根据排列的定义,两个排列相同的充要条件是:两个排列的元素完全相同,且元素的排列顺序也相同.例如,在问题1中,“甲乙”与“甲丙”的元素不完全相同,它们是不同的排列;“甲乙”与“乙甲”虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列.又如,在问题2中,123与134的元素不完全相同,它们是不同的排列;123与132虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列.
典例剖析
例1 某省中学生足球赛预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛?
解:可以先从这6支队中选1支为主队,然后从剩下的5支队中选1支为客队.
按分步乘法计数原理,每组进行的比赛场数为6×5=30.
方法技巧:1.排列问题的判断标准:
(1)元素无重复性;
(2)元素有序性.
2.判断一个计数问题是否为排列问题的关键是看选出的元素有没有顺序要求.
例2 (1)一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
(2)学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少种不同的选法?
解:(1)可以先从这5盘菜中取1盘给同学甲,然后从剩下的4盘菜中取1盘给同学乙,最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理,不同的取法种数为5×4×3=60.
(2)可以先让同学甲从5种菜中选1种,有5种选法;再让同学乙从5种菜中选1种,也有5种选法;最后让同学丙从5种菜中选1种,同样有5种选法.按分步乘法计数原理,不同的选法种数为5×5×5=125.
新知讲解
我们把从????个不同元素中取出????(????≤????)个元素的所有不同排列的个数,叫做从????个不同元素中取出????个元素的排列数,用符号A????????表示.
?
例如,前面问题1是求从3个不同元素中取出2个元素的排列数,表示为A32.
已经算得A32=3×2=6.
问题2是求从4个不同元素中取出3个元素的排列数,表示为A43.
已经算得A43=4×3×2=24.
?
探究:从????个不同元素中取出????个元素的排列数A????????(????≤????)是多少?
?
可以先从特殊情况开始探究,例如求排列数A????2.
根据前面的求解经验,可以这样考虑:
假定有排好顺序的两个空位,如图所示,从????个不同元素中取出2个元素去填空,一个空位填上一个元素,每一种填法就得到一个排列;反之,任何一种排列总可以由这种填法得到.因此,所有不同填法的种数就是排列数A????2.
现在来计算有多少种填法.完成“填空”这件事可以分为两个步骤完成:
第1步,填第1个位置的元素,可以从这????个不同元素中任选1个,有????种选法;
第2步,填第2个位置的元素,可以从剩下的(?????1)个元素中任选1个,有(?????1)种选法.
根据分步乘法计数原理,2个空位的填法种数为A????2=????(?????1).
?
同理,求排列数A????3可以按依次填3个空位来考虑,有A????3=????(?????1)(?????2).
?
一般地,求排列数A????????可以按依次填????个空位来考虑:
假定有排好顺序的????个空位,如图所示,从????个不同元素中取出????个元素去填空,一个空位填上一个元素,每一种填法就对应一个排列.因此,所有不同填法的种数就是排列数A????????.
填空可以分为????个步骤完成:
第1步,从????个不同元素中任选1个填在第1位,有????种选法;
第2步,从剩下的(?????1)个元素中任选1个填在第2位,有(?????1)种选法;
第3步,从剩下的(?????2)个元素中任选1个填在第3位,有(?????2)种选法;
……
第m步,从剩下的[?????(?????1)]个元素中任选1个填在第????位,有(?????????+1)种选法.
根据分步乘法计数原理,????个空位的填法种数为????(?????1)(?????2)…(?????????+1).
这样,我们就得到公式
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}A????????=????(?????1)(?????2)…(?????????+1).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
这里,????,????∈?????,并且????≤????.这个公式叫做排列数公式.
?
特别地,我们把????个不同的元素全部取出的一个排列,叫做????个元素的一个全排列.
这时,排列数公式中????=????,即有
A????????=????(?????1)(?????2)×…×3×2×1.
也就是说,将????个不同的元素全部取出的排列数,等于正整数1到????的连乘积.正整数1到????的连乘积,叫做????的阶乘,用????!表示.于是,????个元素的全排列数公式可以写成
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}A????????=????!.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
另外,我们规定,0!=1.
典例剖析
例3?计算:(1)A37; (2)A47; (3)A77A44; (4)A46×A22.
解:根据排列数公式,可得
(1)A37=7×6×5=210; (2)A47=7×6×5×4=840;
(3)A77A44=7!4!=7×6×5=210; (4)A46×A22=6×5×4×3×2×1=6!=720.
?
思考:由例3可以看到,A73=A77A44=7!4!;A46×A22=6!=A66,即A64=A66A22=6!2!.
观察这两个结果,从中你发现它们的共性了吗?
?
事实上,
Amn=????(?????1)(?????2)…(?????????+1)
=?????????1?????2??????????+1?????????×?×2×1?????????×?×2×1
=A????????A??????????????????=????!?????????!.
因此,排列数公式还可以写成
?
???A????????=?????!??????????!.
提示:(1)在两个排列数公式中,????,????满足的条件都是????,????∈?????,且????≤????.
(2)公式?A????????=????!?????????!的两个作用:
一是当????,????较大时,利用科学计算器计算排列数比较方便;
二是当对含有参数的排列数的式子进行变形和论证时,写成这种形式有利于发现式子之间的关系.
(3)对于阶乘的概念,可以从两个阶乘之间的关系的角度来认识,实际上,较大数的阶乘数一定是较小数的阶乘数的整数倍.
?
例4?用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法1:如图所示,由于三位数的百位上的数字不能是0,所以可以分两步完成:
第1步,确定百位上的数字,可以从1~9这9个数字中取出1个,有A91种取法;
第2步,确定十位和个位上的数字,可以从剩下的9个数字中取出2个,有A92种取法.
根据分步乘法计数原理,所求的三位数的个数为A91×A92=9×9×8=648.
?
解法2:如图所示,符合条件的三位数可以分成三类:第1类,每一位数字都不是0的三位数,可以从1~9这9个数字中取出3个,有A93种取法;第2类,个位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和十位,有A92种取法;第3类,十位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和个位,有A92种取法.
根据分类加法计数原理,所求三位数的个数为 A93+A92+A92=9×8×7+9×8+9×8=648.
?
解法3:从0~9这10个数字中选取3个的排列数为,其中0在百位上的排列数为A92,它们的差就是用这10个数组成的没有重复数字的三位数的个数,即所求三位数的个数为
A103-A92=10×9×8-9×8=648.
?
点评:对于例4这类计数问题,从不同的角度就有不同的解题方法.
解法1根据百位数字不能是0的要求,按分步乘法计数原理完成从10个数中取出3个数组成没有重复数字的三位数这件事;
解法2是以0是否出现以及出现的位置为标准,按分类加法计数原理完成这件事;解法3是一种间接法,先求出从10个数中取出3个数的排列数,然后减去其中百位是0的排列数(不是三位数的个数),就得到没有重复数字的三位数的个数.
随堂小测
1.(1)已知A2n=56,那么????= .
(2)计算A2????????+3+A3????= .
?
8
726
2. 将4名医生与4名护士分配到四个不同单位,每个单位分配一名医生与一名护士,共有多少种不同的分配方案?
解:完成这件事可以分为两步.
第一步:把4名医生分配到四个不同的单位,等价于从4个不同元素中取出4个元素的排列问题,有A44种方法.
第二步:把4名护士分配到四个不同的单位,也有A44种方法.
根据分步乘法计数原理,不同的分配方案有A44×A44=576种.
?
3. 6本不同的书在书桌上摆成一排,要求甲、乙两本书必须放在两端,丙、丁两本书必须相邻,则不同的摆放方法有( )种.
A.24 B.36 C.48 D.60
A
4.现有5人要排成一排照相,其中甲与乙两人不相邻,且甲不站在两端,则不同的排法有 种.(用数字作答)
36
课堂小结
排列:一般地,从????个不同元素中取出????(????≤????)个元素,并按照一定的顺序排成一列,叫做从????个不同元素中取出????个元素的一个排列.
?
排列与排列数的概念:
排列数:我们把从????个不同元素中取出????(????≤????)个元素的所有不同排列的个数,叫做从????个不同元素中取出????个元素的排列数,用符号A????????表示.
?
排列数公式:
???A????????=?????!??????????!=????(?????1)(?????2)…(?????????+1)
?
A????????=????!=????(?????1)(?????2)×…×3×2×1
?
谢 谢!
