高中数学选择性必修第三册RJ·A--6.2 排列与组合-6.2.3 组合 6.2.4 组合数课件 课件(共18张ppt)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·A--6.2 排列与组合-6.2.3 组合 6.2.4 组合数课件 课件(共18张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 20:56:05 | ||
图片预览






文档简介
第六章
6.2
排列与组合
6.2.3 组合
6.2.4 组合数
学习目标
1.理解组合、组合数的概念及组合和排列之间的区别与联系.
2.能利用计数原理推导组合数公式,并熟练掌握组合数公式及组合数的性质,能运用组合数的性质化简、计算、证明.
3.能运用排列数公式、组合数公式和计数原理解决一些简单的应用问题,提高数学应用能力和分析问题、解决问题的能力.
核心素养:逻辑推理、数学运算、数学建模.
新知学习
探究:从甲、乙、丙3名同学中选2名去参加一项活动,有多少种不同的选法?
这一问题与6.2.1节的问题1有什么联系与区别?
从6.2.1节问题1的6种选法中,存在“甲上午、乙下午”和“乙上午、甲下午”2种不同顺序的选法,我们可以将它看成是先选出甲、乙2名同学,然后再分配上午和下午而得到的.同样,先选出甲、丙或乙、丙,再分配上午和下午也都各有2种方法.而从甲、乙、丙3名同学中选2名去参加一项活动,就只需考虑将选出的2名同学作为一组,不需要考虑他们的顺序.于是,在6.2.1节问题1的6种选法中,将选出的2名同学作为一组的选法就只有如下3种情况:
甲乙,甲丙,乙丙.
将具体背景舍去,上述问题可以概括为:
从3个不同元素中取出2个元素作为一组,一共有多少个不同的组?
新知讲解
一般地,从????个不同元素中取出????(????≤????)个元素作为一组,叫做从????个不同元素中取出????个元素的一个组合(combination).
?
思考:你能说一说排列与组合之间的联系与区别吗?
从排列与组合的定义可以知道,两者都是从????个不同元素中取出????(????≤????)个元素,这是它们的共同点.但排列与元素的顺序有关,而组合与元素的顺序无关.只有元素相同且顺序也相同的两个排列才是相同的;而两个组合只要元素相同,不论元素的顺序如何,都是相同的.例如,在上述探究问题中,“甲乙”与“乙甲”的元素完全相同,但元素的排列顺序不同,因此它们是相同的组合,但不是相同的排列.由此,以“元素相同”为标准分类,就可以建立起排列和组合之间的对应关系,如图所示.
?
思考:校门口停放着9辆共享自行车,其中黄色、红色和绿色的各有3辆.
下面的问题是排列问题,还是组合问题?
(1)从中选3辆,有多少种不同的方法?
(2)从中选3辆给3位同学,有多少种不同的方法?
在(1)中,选出3辆车即可,没有顺序,是一个组合问题;
在(2)中,不仅要选出3辆车,还要分配给3位同学,有顺序,是一个排列问题.
典例剖析
例5 平面内有A,B,C,D共4个点.
(1)以其中2个点为端点的有向线段共有多少条?
(2)以其中2个点为端点的线段共有多少条?
解:(1)一条有向线段的两个端点要分起点和终点,以平面内4个点中的2个为端点的有向线段的条数,就是从4个不同元素中取出2个元素的排列数,即有向线段条数为
A24=4×3=12.
这12条有向线段分别为 ????????,????????,????????,????????,????????,????????,????????,????????,????????,????????,????????,????C.
(2)由于不考虑两个端点的顺序,因此将(1)中端点相同、方向不同的2条有向线段作为一条线段,就是以平面内4个点中的2个点为端点的线段的条数,共有如下6条:
AB,AC,AD,BC,BD,CD.
?
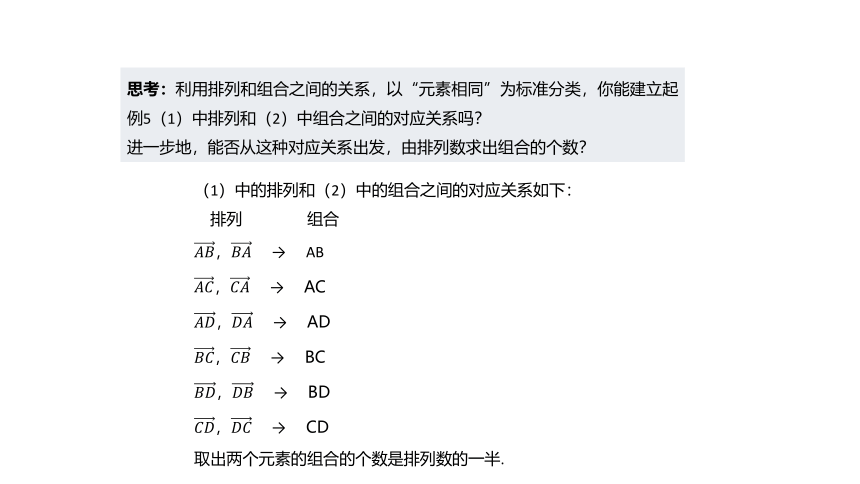
思考:利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之间的对应关系吗?
进一步地,能否从这种对应关系出发,由排列数求出组合的个数?
(1)中的排列和(2)中的组合之间的对应关系如下:
排列 组合
????????,???????? → AB
????????,???????? → AC
????????,???????? → AD
????????,???????? → BC
????????,???????? → BD
????????,???????? → CD
取出两个元素的组合的个数是排列数的一半.
?
新知讲解
从????个不同元素中取出????(????≤????)个元素的所有不同组合的个数,叫做从????个不同元素中取出????个元素的组合数,用符号C?????????表示.
例如,从3个不同元素中取出2个元素的组合数表示为C23,从4个不同元素中取出3个元素的组合数表示为C34.
?
探究:前面已经提到,组合和排列有关系,我们能否利用这种关系,由排列数A????????来求组合数C????????呢?
?
前面,我们利用“元素相同、顺序不同的两个组合相同”“元素相同、顺序不同的两个排列不同”,以“元素相同”为标准,建立了排列和组合之间的对应关系,并求得了从3个不同元素中取出2个元素的组合数C23=3.
运用同样的方法,我们来求从4个不同元素中取出3个元素的组合数????34.设这4个元素为????,????,????,????,那么从中取出3个元素的排列数A34=24,以“元素相同”为标准将这24个排列分组,一共有4组,如图所示,因此组合数C34=4.
?
观察上图,也可以这样理解求“从4个元素中取出3个元素的排列数????34”:
第1步,从4个元素中取出3个元素作为一组,共有C34种不同的取法;
第2步,将取出的3个元素作全排列,共有????33种不同的排法.
于是,根据分步乘法计数原理,有A34=C34·A33,即C34=A43A33=4.
?
同样地,求“从????个元素中取出????个元素的排列数A????????”,可以看作由以下两个步骤得到:
第1步,从????个不同元素中取出????个元素作为一组,共有C????????种不同的取法;
第2步,将取出的????个元素作全排列,共有A????????种不同的排法.
根据分步乘法计数原理,有A????????=C????????·A????????.
因此
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}C????????=A????????A????????=?????????1?????2…?????????+1?????!.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
这里????,????∈?????,并且????≤????.这个公式叫做组合数公式.
?
因为A????????=?????!??????????!,
所以,上面的组合数公式还可以写成
?
C????????=?????!?????!??????????!.
另外,我们规定C????0=1.
?
提示:(1)对组合数公式C????????应注意两点:
①它的值是一个非零自然数;②????,????∈?????,且????≤????.
(2)在学习组合数公式时,要注意与排列数公式进行对比.
组合数公式1一般用于求值计算;
组合数公式2一般用于化简与证明,因为这个公式便于整体约分化简.
?
典例剖析
例6?计算:(1)C310;(2)C710;(3)C1010;(4)C010.
解:根据组合数公式,可得
(1)C310=A103A33=10×9×83!=120;
(2)C710=10!7!10?7!=10×9×8×7!7!×3!=10×9×83!=120;
(3)C1010=A1010A1010=10!10!=1;
(4)C010=1.
?
思考:观察例6的(1)与(2),(3)与(4)的结果,你有什么发现?
(1)与(2)分别用了不同形式的组合数公式,你对公式的选择有什么想法?
新知讲解
组合数的两个性质
性质1 C????????=C?????????????.
?
性质2 C????+1????=C????????+C?????????1.
?
例7?在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
解:(1)所有的不同抽法种数,就是从100件产品中抽出3件的组合数,
所以抽法种数为C3100=A1003A33=100×99×983!=161 700;
(2)从2件次品中抽出1件的抽法有C12种,从98件合格品中抽出2件的抽法有C298种,
因此抽出的3件中恰好有1件次品的抽法种数为C12×C298=2×98×972!=9 506.
?
(3)方法1 从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为C12×C298+C22×C198=9 506+98=9 604.
方法2 抽出的3件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即C3100-C398=161 700-98×97×963!=9 604.
?
随堂小测
1.计算:(1)C83-2C62;
(2)C104-C73·A33.
?
26
0
2.某班级要从4名男生,2名女生中选派4人参加某次社区服务活动,如果要求至少有1名女生,那么不同的选派方案种数为 ( )
A.14 B.24 C.28 D.48
A
3.为了配合创建全国文明城市的活动,某校现从4名男教师和5名女教师中选取3人组成创文明志愿者小组,若男女教师至少各有一人,则不同的选法共有 ( )
A.140种 B.84种 C.70种 D.35种
C
4.从0,1,2,3,4,5这六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数的个数为 ( )
A.300 B.216 C.180 D.162
C
课堂小结
组合与组合数的概念:
组合数公式:
组合:一般地,从????个不同元素中取出????(????≤????)个元素作为一组,叫做从????个不同元素中取出????个元素的一个组合.
?
组合数:从????个不同元素中取出????(????≤????)个元素的所有不同组合的个数,叫做从????个不同元素中取出????个元素的组合数,用符号C?????????表示.
?
C????????=A????????A????????=?????????1?????2…?????????+1?????!.
?
C????????=?????!?????!??????????!.
?
规定:C????0=1.
?
谢 谢!
6.2
排列与组合
6.2.3 组合
6.2.4 组合数
学习目标
1.理解组合、组合数的概念及组合和排列之间的区别与联系.
2.能利用计数原理推导组合数公式,并熟练掌握组合数公式及组合数的性质,能运用组合数的性质化简、计算、证明.
3.能运用排列数公式、组合数公式和计数原理解决一些简单的应用问题,提高数学应用能力和分析问题、解决问题的能力.
核心素养:逻辑推理、数学运算、数学建模.
新知学习
探究:从甲、乙、丙3名同学中选2名去参加一项活动,有多少种不同的选法?
这一问题与6.2.1节的问题1有什么联系与区别?
从6.2.1节问题1的6种选法中,存在“甲上午、乙下午”和“乙上午、甲下午”2种不同顺序的选法,我们可以将它看成是先选出甲、乙2名同学,然后再分配上午和下午而得到的.同样,先选出甲、丙或乙、丙,再分配上午和下午也都各有2种方法.而从甲、乙、丙3名同学中选2名去参加一项活动,就只需考虑将选出的2名同学作为一组,不需要考虑他们的顺序.于是,在6.2.1节问题1的6种选法中,将选出的2名同学作为一组的选法就只有如下3种情况:
甲乙,甲丙,乙丙.
将具体背景舍去,上述问题可以概括为:
从3个不同元素中取出2个元素作为一组,一共有多少个不同的组?
新知讲解
一般地,从????个不同元素中取出????(????≤????)个元素作为一组,叫做从????个不同元素中取出????个元素的一个组合(combination).
?
思考:你能说一说排列与组合之间的联系与区别吗?
从排列与组合的定义可以知道,两者都是从????个不同元素中取出????(????≤????)个元素,这是它们的共同点.但排列与元素的顺序有关,而组合与元素的顺序无关.只有元素相同且顺序也相同的两个排列才是相同的;而两个组合只要元素相同,不论元素的顺序如何,都是相同的.例如,在上述探究问题中,“甲乙”与“乙甲”的元素完全相同,但元素的排列顺序不同,因此它们是相同的组合,但不是相同的排列.由此,以“元素相同”为标准分类,就可以建立起排列和组合之间的对应关系,如图所示.
?
思考:校门口停放着9辆共享自行车,其中黄色、红色和绿色的各有3辆.
下面的问题是排列问题,还是组合问题?
(1)从中选3辆,有多少种不同的方法?
(2)从中选3辆给3位同学,有多少种不同的方法?
在(1)中,选出3辆车即可,没有顺序,是一个组合问题;
在(2)中,不仅要选出3辆车,还要分配给3位同学,有顺序,是一个排列问题.
典例剖析
例5 平面内有A,B,C,D共4个点.
(1)以其中2个点为端点的有向线段共有多少条?
(2)以其中2个点为端点的线段共有多少条?
解:(1)一条有向线段的两个端点要分起点和终点,以平面内4个点中的2个为端点的有向线段的条数,就是从4个不同元素中取出2个元素的排列数,即有向线段条数为
A24=4×3=12.
这12条有向线段分别为 ????????,????????,????????,????????,????????,????????,????????,????????,????????,????????,????????,????C.
(2)由于不考虑两个端点的顺序,因此将(1)中端点相同、方向不同的2条有向线段作为一条线段,就是以平面内4个点中的2个点为端点的线段的条数,共有如下6条:
AB,AC,AD,BC,BD,CD.
?
思考:利用排列和组合之间的关系,以“元素相同”为标准分类,你能建立起例5(1)中排列和(2)中组合之间的对应关系吗?
进一步地,能否从这种对应关系出发,由排列数求出组合的个数?
(1)中的排列和(2)中的组合之间的对应关系如下:
排列 组合
????????,???????? → AB
????????,???????? → AC
????????,???????? → AD
????????,???????? → BC
????????,???????? → BD
????????,???????? → CD
取出两个元素的组合的个数是排列数的一半.
?
新知讲解
从????个不同元素中取出????(????≤????)个元素的所有不同组合的个数,叫做从????个不同元素中取出????个元素的组合数,用符号C?????????表示.
例如,从3个不同元素中取出2个元素的组合数表示为C23,从4个不同元素中取出3个元素的组合数表示为C34.
?
探究:前面已经提到,组合和排列有关系,我们能否利用这种关系,由排列数A????????来求组合数C????????呢?
?
前面,我们利用“元素相同、顺序不同的两个组合相同”“元素相同、顺序不同的两个排列不同”,以“元素相同”为标准,建立了排列和组合之间的对应关系,并求得了从3个不同元素中取出2个元素的组合数C23=3.
运用同样的方法,我们来求从4个不同元素中取出3个元素的组合数????34.设这4个元素为????,????,????,????,那么从中取出3个元素的排列数A34=24,以“元素相同”为标准将这24个排列分组,一共有4组,如图所示,因此组合数C34=4.
?
观察上图,也可以这样理解求“从4个元素中取出3个元素的排列数????34”:
第1步,从4个元素中取出3个元素作为一组,共有C34种不同的取法;
第2步,将取出的3个元素作全排列,共有????33种不同的排法.
于是,根据分步乘法计数原理,有A34=C34·A33,即C34=A43A33=4.
?
同样地,求“从????个元素中取出????个元素的排列数A????????”,可以看作由以下两个步骤得到:
第1步,从????个不同元素中取出????个元素作为一组,共有C????????种不同的取法;
第2步,将取出的????个元素作全排列,共有A????????种不同的排法.
根据分步乘法计数原理,有A????????=C????????·A????????.
因此
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}C????????=A????????A????????=?????????1?????2…?????????+1?????!.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
这里????,????∈?????,并且????≤????.这个公式叫做组合数公式.
?
因为A????????=?????!??????????!,
所以,上面的组合数公式还可以写成
?
C????????=?????!?????!??????????!.
另外,我们规定C????0=1.
?
提示:(1)对组合数公式C????????应注意两点:
①它的值是一个非零自然数;②????,????∈?????,且????≤????.
(2)在学习组合数公式时,要注意与排列数公式进行对比.
组合数公式1一般用于求值计算;
组合数公式2一般用于化简与证明,因为这个公式便于整体约分化简.
?
典例剖析
例6?计算:(1)C310;(2)C710;(3)C1010;(4)C010.
解:根据组合数公式,可得
(1)C310=A103A33=10×9×83!=120;
(2)C710=10!7!10?7!=10×9×8×7!7!×3!=10×9×83!=120;
(3)C1010=A1010A1010=10!10!=1;
(4)C010=1.
?
思考:观察例6的(1)与(2),(3)与(4)的结果,你有什么发现?
(1)与(2)分别用了不同形式的组合数公式,你对公式的选择有什么想法?
新知讲解
组合数的两个性质
性质1 C????????=C?????????????.
?
性质2 C????+1????=C????????+C?????????1.
?
例7?在100件产品中,有98件合格品,2件次品.从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
解:(1)所有的不同抽法种数,就是从100件产品中抽出3件的组合数,
所以抽法种数为C3100=A1003A33=100×99×983!=161 700;
(2)从2件次品中抽出1件的抽法有C12种,从98件合格品中抽出2件的抽法有C298种,
因此抽出的3件中恰好有1件次品的抽法种数为C12×C298=2×98×972!=9 506.
?
(3)方法1 从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为C12×C298+C22×C198=9 506+98=9 604.
方法2 抽出的3件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即C3100-C398=161 700-98×97×963!=9 604.
?
随堂小测
1.计算:(1)C83-2C62;
(2)C104-C73·A33.
?
26
0
2.某班级要从4名男生,2名女生中选派4人参加某次社区服务活动,如果要求至少有1名女生,那么不同的选派方案种数为 ( )
A.14 B.24 C.28 D.48
A
3.为了配合创建全国文明城市的活动,某校现从4名男教师和5名女教师中选取3人组成创文明志愿者小组,若男女教师至少各有一人,则不同的选法共有 ( )
A.140种 B.84种 C.70种 D.35种
C
4.从0,1,2,3,4,5这六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数的个数为 ( )
A.300 B.216 C.180 D.162
C
课堂小结
组合与组合数的概念:
组合数公式:
组合:一般地,从????个不同元素中取出????(????≤????)个元素作为一组,叫做从????个不同元素中取出????个元素的一个组合.
?
组合数:从????个不同元素中取出????(????≤????)个元素的所有不同组合的个数,叫做从????个不同元素中取出????个元素的组合数,用符号C?????????表示.
?
C????????=A????????A????????=?????????1?????2…?????????+1?????!.
?
C????????=?????!?????!??????????!.
?
规定:C????0=1.
?
谢 谢!
