高中数学选择性必修第三册RJ·A--7.4 二项分布与超几何分布-7.4.1 二项分布 课件(共21张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·A--7.4 二项分布与超几何分布-7.4.1 二项分布 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 00:00:00 | ||
图片预览







文档简介
第七章
7.4
二项分布与超几何分布
7.4.1 二项分布
学习目标
1.通过具体实例,了解伯努利试验与n重伯努利试验.
2.通过具体实例,掌握二项分布及其数字特征,并能解决简单的实际问题.
核心素养:数学建模、逻辑推理、数学抽象、数学运算.
新知学习
在实际问题中,有许多随机试验与掷硬币试验具有相同的特征,它们只包含两个可能结果.例如,检验一件产品结果为合格或不合格,飞碟射击时中靶或脱靶,医学检验结果为阳性或阴性等.我们把只包含两个可能结果的试验叫做伯努利试验.
我们将一个伯努利试验独立地重复进行????次所组成的随机试验称为????重伯努利试验.
显然,????重伯努利试验具有如下共同特征:
(1)同一个伯努利试验重复做????次;
(2)各次试验的结果相互独立.
?
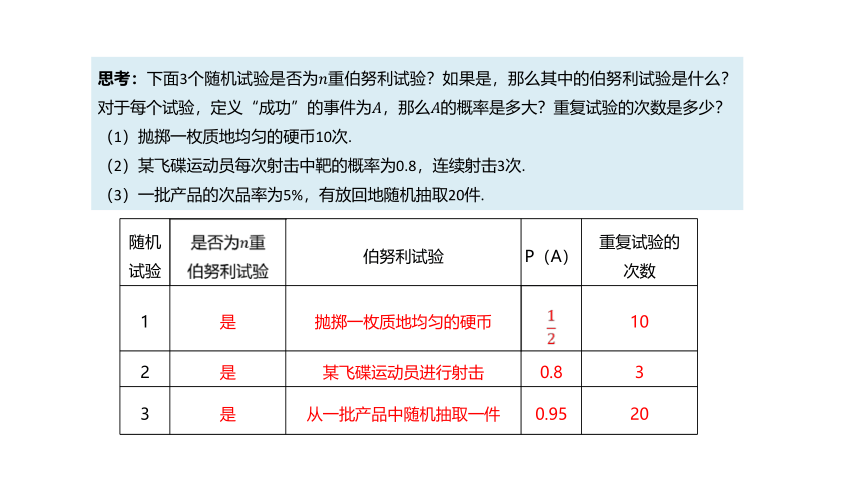
思考:下面3个随机试验是否为????重伯努利试验?如果是,那么其中的伯努利试验是什么?对于每个试验,定义“成功”的事件为????,那么????的概率是多大?重复试验的次数是多少?
(1)抛掷一枚质地均匀的硬币10次.
(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.
(3)一批产品的次品率为5%,有放回地随机抽取20件.
?
随机
试验
是否为????重
伯努利试验
伯努利试验
P(A)
重复试验的
次数
1
是
抛掷一枚质地均匀的硬币
12
10
2
是
某飞碟运动员进行射击
0.8
3
3
是
从一批产品中随机抽取一件
0.95
20
随机
试验
伯努利试验
P(A)
重复试验的
次数
1
是
抛掷一枚质地均匀的硬币
10
2
是
某飞碟运动员进行射击
0.8
3
3
是
从一批产品中随机抽取一件
0.95
20
在伯努利试验中,我们关注某个事件????是否发生,而在????重伯努利试验中,我们关注事件????发生的次数????.进一步地,因为????是一个离散型随机变量,所以我们实际关心的是它的概率分布列.例如,对产品抽样检验,随机抽取????件,我们关心样本中不合格品数的概率分布列.
?
探究:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数????的概率分布列是怎样的?
?
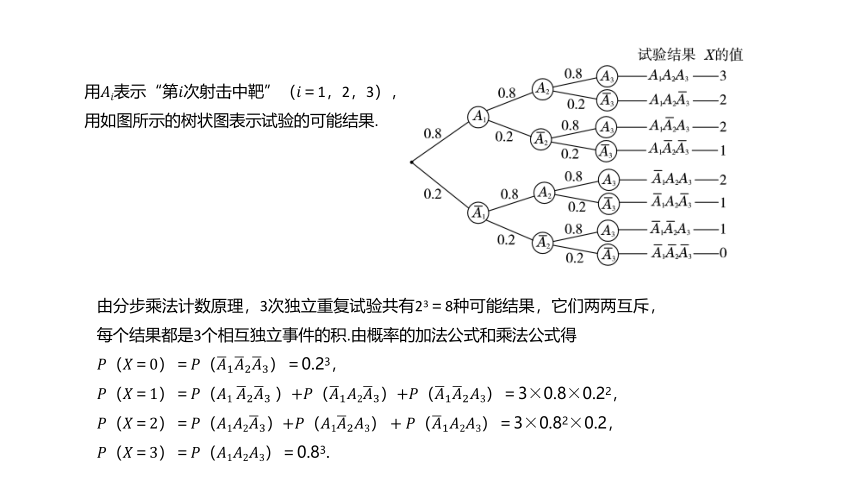
用????????表示“第????次射击中靶”(????=1,2,3),
用如图所示的树状图表示试验的可能结果.
?
由分步乘法计数原理,3次独立重复试验共有23=8种可能结果,它们两两互斥,每个结果都是3个相互独立事件的积.由概率的加法公式和乘法公式得
????(????=0)=????(????1????2????3)=0.23,
????(????=1)=????(????1?????2????3?)+????(????1????2????3)+????(????1????2????3)=3×0.8×0.22,
????(????=2)=????(????1????2????3)+????(????1????2????3)+????(????1????2????3)=3×0.82×0.2,
????(????=3)=????(????1????2????3)=0.83.
?
为了简化表示,每次射击用1表示中靶,用0表示脱靶,那么3次射击恰好2次中靶的所有可能结果可表示为011,110,101,这三个结果发生的概率都相等,均为0.82×0.2,并且与哪两次中靶无关.因此,3次射击恰好2次中靶的概率为C32?×0.82×0.2.
同理可求中靶0次、1次、3次的概率.于是,中靶次数????的分布列为
????(????=????)= C3?????×0.8????×0.23?????,????=0,1,2,3.
?
思考:如果连续射击4次,类比上面的分析,表示中靶次数????等于2的结果有哪些?
写出中靶次数????的分布列.
?
提示:(1)表示中靶次数????等于2的结果有: ????1????2????3????4,????1????2????3????4,????1????2????3????4,????1 ????2????3????4,????1????2????3????4,????1 ????2????3????4,共6个.
(2)中靶次数????的分布列为????(????=????)= C4?????×0.8????×0.24?????,????=0,1,2,3,4.
?
新知讲解
一般地,在????重伯努利试验中,设每次试验中事件????发生的概率为????(0?
如果随机变量????的分布列具有上式的形式,则称随机变量????服从二项分布,记作????~????(????,????).
?
理解二项分布应注意的问题
(1)对于公式????(????=????)=C????????????????(1?????)?????????(????=0,1,2,…,????)必须在满足“独立重复试验”时才能运用,否则不能应用该公式.
(2)正确理解其条件以及参数????,????,????的意义是运用公式的前提,一般含有“恰好”“恰有”等字样的问题往往考虑独立重复试验的模型.
(3)判断一个随机变量是否服从二项分布,关键有两点:一是对立性,即一次试验中,事件发生与否两者必有其一;二是重复性,即试验是独立重复地进行了????次.
?
典例剖析
例1 将一枚质地均匀的硬币重复抛掷10次,求:
(1)恰好出现5次正面朝上的概率;
(2)正面朝上出现的频率在[0.4,0.6]内的概率.
解:设????=“正面朝上”,则????(????)=0.5.用????表示事件????发生的次数,则 ????~????(10,0.5).
(1)恰好出现5次正面朝上等价于????=5,于是
????(????=5)= C105?×0.510=2521?024=63256;
(2)正面朝上出现的频率在[0.4,0.6]内等价于4≤????≤6,于是
????(4≤????≤6)=?C104?×0.510+ C105?×0.510+ C106?×0.510=6721?024=2132.
?
例2 如图是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落的过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中.格子从左到右分别编号为0,1,2,…,10,用X表示小球最后落入格子的号码,求X的分布列.
解:设????=“向右下落”,则????=“向左下落”,且????(????)=????(????)=0.5.
因为小球最后落入格子的号码????等于事件????发生的次数,而小球在下落的
过程中共碰撞小木钉10次,所以????~????(10,0.5).
于是,????的分布列为
????(????=????)=C10????×0.510,????=0,1,2,…,10.
????的概率分布图如图所示.
?
例3 甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利?
解法1:采用3局2胜制,甲最终获胜有两种可能的比分2∶0或2∶1,前者是前两局甲连胜,后者是前两局甲、乙各胜一局且第3局甲胜.因为每局比赛的结果是独立的,甲最终获胜的概率为
????1=0.62+C21×0.62×0.4=0.648.
类似地,采用5局3胜制,甲最终获胜有3种比分3∶0,3∶1或3∶2.因为每局比赛的结果是独立的,所以甲最终获胜的概率为
??????2=0.63+C32×0.63×0.4+C42×0.63×0.42=0.682?56.
?
解法2:采用3局2胜制,不妨设赛满3局,用????表示3局比赛中甲胜的局数,则????~????(3,0.6).甲最终获胜的概率为
????1=????(????=2)+????(????=3)=C32×0.62×0.4+C33×0.63=0.648.
采用5局3胜制,不妨设赛满5局,用????表示5局比赛中甲胜的局数,则????~????(5,0.6).甲最终获胜的概率为
????2=????(????=3)+????(????=4)+????(????=5)
=C53×0.63×0.42+C54×0.64×0.4+C55×0.65
=0.682?56.
因为????2>????1,所以5局3胜制对甲有利.实际上,比赛局数越多,对实力较强者越有利.
?
归纳总结:一般地,确定一个二项分布模型的步骤如下:
(1)明确伯努利试验及事件????的意义,确定事件????发生的概率????;
(2)确定重复试验的次数????,并判断各次试验的独立性;
(3)设????为????次独立重复试验中事件????发生的次数,则????~????(????,????).
?
探究:假设随机变量????服从二项分布????(????,????),那么????的均值和方差各是什么?
?
我们知道,抛掷一枚质地均匀的硬币,“正面朝上”的概率为0.5,如果掷100次硬币,期望有100×0.5=50次正面朝上.根据均值的含义,对于服从二项分布的随机变量????,我们猜想????(????)=????????.
我们不妨从简单开始,先考察????较小的情况.
(1)当????=1时,????服从两点分布,分布列为
????(????=0)=1?????,????(????=1)=????.
均值和方差分别为
????(????)=????,????(????)=????(1?????).
(2)当????=2时,????的分布列为
????(????=0)=(1?????)2,????(????=1)=2????(1?????),????(????=2)=????2.
均值和方差分别为
??????????(????)=0×(1?????)2+1×2????(1?????)+2×????2=2????.
??????(????)=02×(1?????)2+12×2????(1?????)+22×????2?(2????)2=2????(1?????).
?
一般地,可以证明:
如果????~????(????,????),那么????(????)=????????,????(????)=????????(1?????).
?
对均值的证明:
令????=1?????,由????C????????=C?????1?????1,可得
????(????)= ????C?????????????????????????????= C?????1?????1??????????????????????=???????? C?????1?????1?????????1?????????1?(?????1)?.
令?????1=????,则
????????=??????????????? C?????1?????????????????????1?????=????????????+?????????1=????????.
?
对方差的证明:
????????=?????(?????????(????))2 C????????????????1??????????????=????(????2?2????????????+(????????)2)C????????????????1???????????????
= ????2 C????????????????1????????????????2????????????????? C????????????????1???????????????+(????????)2???????C????????????????1???????????????
= ????2?C????????????????1????????????????2(????????)2+(????????)2= ????2 C????????????????1????????????????(????????)2,
又 ????2 C????????????????1???????????????=???(????(?????1)+????)?C????????????????1???????????????
= ?????????1C????????????????1??????????????+????????C????????????????1??????????????
=?????????1????2???????????2!?????2!?????2??????2!?????????21??????????2?(?????2)+????????
=?????????1????2?????C?????2????????????1??????????2?????+????????
=????(?????1)????2+????????,
因此????(????)=????(?????1)????2+?????????(????????)2=?????????????????2=????????(1?????).
?
随堂小测
1.有8件产品,其中4件是次品,从中有放回地取3次(每次1件),若????表示取得次品的次数,则????(????≤2)= ( )
A. 38 B. 1314 C. 45 D. 78
?
D
2.已知随机变量????+????=8,若????~????(10,0.4),则????(????),????(????)分别是( )
A.4和2.4 B.2和2.4 C.6和2.4 D.4和5.6
?
A
3.若随机变量????~????(????,????),且????(????)=52,????(????)=54,则????(????=1)= .(用数字作答)
?
532
?
4.某次考试共有12个选择题,每个选择题的分值为5分,每个选择题四个选项且只有一个选项是正确的,A学生对12个选择题中每个题的四个选项都没有把握,最后选择题的得分为????分,B学生对12个选择题中每个题的四个选项都能判断其中有一个选项是错误的,对其他三个选项都没有把握,最后选择题的得分为????分.则????(????)?????(????)的值为( )
A.12512 B.3512 C . 274 D.234
?
A
课堂小结
伯努利试验 与?????重伯努利试验
?
一般地,在????重伯努利试验中,设每次试验中事件????发生的概率为????(0?
二项分布
确定一个二项分布模型的步骤
(1)明确伯努利试验及事件????的意义,确定事件????发生的概率????;
(2)确定重复试验的次数????,并判断各次试验的独立性;
(3)设????为????次独立重复试验中事件????发生的次数,则????~????(????,????).
?
假设随机变量????服从二项分布????(????,????),那么
?
????(????)=????,????(????)=????(1?????).
?
二项分布的均值与方差
谢 谢!
7.4
二项分布与超几何分布
7.4.1 二项分布
学习目标
1.通过具体实例,了解伯努利试验与n重伯努利试验.
2.通过具体实例,掌握二项分布及其数字特征,并能解决简单的实际问题.
核心素养:数学建模、逻辑推理、数学抽象、数学运算.
新知学习
在实际问题中,有许多随机试验与掷硬币试验具有相同的特征,它们只包含两个可能结果.例如,检验一件产品结果为合格或不合格,飞碟射击时中靶或脱靶,医学检验结果为阳性或阴性等.我们把只包含两个可能结果的试验叫做伯努利试验.
我们将一个伯努利试验独立地重复进行????次所组成的随机试验称为????重伯努利试验.
显然,????重伯努利试验具有如下共同特征:
(1)同一个伯努利试验重复做????次;
(2)各次试验的结果相互独立.
?
思考:下面3个随机试验是否为????重伯努利试验?如果是,那么其中的伯努利试验是什么?对于每个试验,定义“成功”的事件为????,那么????的概率是多大?重复试验的次数是多少?
(1)抛掷一枚质地均匀的硬币10次.
(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.
(3)一批产品的次品率为5%,有放回地随机抽取20件.
?
随机
试验
是否为????重
伯努利试验
伯努利试验
P(A)
重复试验的
次数
1
是
抛掷一枚质地均匀的硬币
12
10
2
是
某飞碟运动员进行射击
0.8
3
3
是
从一批产品中随机抽取一件
0.95
20
随机
试验
伯努利试验
P(A)
重复试验的
次数
1
是
抛掷一枚质地均匀的硬币
10
2
是
某飞碟运动员进行射击
0.8
3
3
是
从一批产品中随机抽取一件
0.95
20
在伯努利试验中,我们关注某个事件????是否发生,而在????重伯努利试验中,我们关注事件????发生的次数????.进一步地,因为????是一个离散型随机变量,所以我们实际关心的是它的概率分布列.例如,对产品抽样检验,随机抽取????件,我们关心样本中不合格品数的概率分布列.
?
探究:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数????的概率分布列是怎样的?
?
用????????表示“第????次射击中靶”(????=1,2,3),
用如图所示的树状图表示试验的可能结果.
?
由分步乘法计数原理,3次独立重复试验共有23=8种可能结果,它们两两互斥,每个结果都是3个相互独立事件的积.由概率的加法公式和乘法公式得
????(????=0)=????(????1????2????3)=0.23,
????(????=1)=????(????1?????2????3?)+????(????1????2????3)+????(????1????2????3)=3×0.8×0.22,
????(????=2)=????(????1????2????3)+????(????1????2????3)+????(????1????2????3)=3×0.82×0.2,
????(????=3)=????(????1????2????3)=0.83.
?
为了简化表示,每次射击用1表示中靶,用0表示脱靶,那么3次射击恰好2次中靶的所有可能结果可表示为011,110,101,这三个结果发生的概率都相等,均为0.82×0.2,并且与哪两次中靶无关.因此,3次射击恰好2次中靶的概率为C32?×0.82×0.2.
同理可求中靶0次、1次、3次的概率.于是,中靶次数????的分布列为
????(????=????)= C3?????×0.8????×0.23?????,????=0,1,2,3.
?
思考:如果连续射击4次,类比上面的分析,表示中靶次数????等于2的结果有哪些?
写出中靶次数????的分布列.
?
提示:(1)表示中靶次数????等于2的结果有: ????1????2????3????4,????1????2????3????4,????1????2????3????4,????1 ????2????3????4,????1????2????3????4,????1 ????2????3????4,共6个.
(2)中靶次数????的分布列为????(????=????)= C4?????×0.8????×0.24?????,????=0,1,2,3,4.
?
新知讲解
一般地,在????重伯努利试验中,设每次试验中事件????发生的概率为????(0?
如果随机变量????的分布列具有上式的形式,则称随机变量????服从二项分布,记作????~????(????,????).
?
理解二项分布应注意的问题
(1)对于公式????(????=????)=C????????????????(1?????)?????????(????=0,1,2,…,????)必须在满足“独立重复试验”时才能运用,否则不能应用该公式.
(2)正确理解其条件以及参数????,????,????的意义是运用公式的前提,一般含有“恰好”“恰有”等字样的问题往往考虑独立重复试验的模型.
(3)判断一个随机变量是否服从二项分布,关键有两点:一是对立性,即一次试验中,事件发生与否两者必有其一;二是重复性,即试验是独立重复地进行了????次.
?
典例剖析
例1 将一枚质地均匀的硬币重复抛掷10次,求:
(1)恰好出现5次正面朝上的概率;
(2)正面朝上出现的频率在[0.4,0.6]内的概率.
解:设????=“正面朝上”,则????(????)=0.5.用????表示事件????发生的次数,则 ????~????(10,0.5).
(1)恰好出现5次正面朝上等价于????=5,于是
????(????=5)= C105?×0.510=2521?024=63256;
(2)正面朝上出现的频率在[0.4,0.6]内等价于4≤????≤6,于是
????(4≤????≤6)=?C104?×0.510+ C105?×0.510+ C106?×0.510=6721?024=2132.
?
例2 如图是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落的过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中.格子从左到右分别编号为0,1,2,…,10,用X表示小球最后落入格子的号码,求X的分布列.
解:设????=“向右下落”,则????=“向左下落”,且????(????)=????(????)=0.5.
因为小球最后落入格子的号码????等于事件????发生的次数,而小球在下落的
过程中共碰撞小木钉10次,所以????~????(10,0.5).
于是,????的分布列为
????(????=????)=C10????×0.510,????=0,1,2,…,10.
????的概率分布图如图所示.
?
例3 甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利?
解法1:采用3局2胜制,甲最终获胜有两种可能的比分2∶0或2∶1,前者是前两局甲连胜,后者是前两局甲、乙各胜一局且第3局甲胜.因为每局比赛的结果是独立的,甲最终获胜的概率为
????1=0.62+C21×0.62×0.4=0.648.
类似地,采用5局3胜制,甲最终获胜有3种比分3∶0,3∶1或3∶2.因为每局比赛的结果是独立的,所以甲最终获胜的概率为
??????2=0.63+C32×0.63×0.4+C42×0.63×0.42=0.682?56.
?
解法2:采用3局2胜制,不妨设赛满3局,用????表示3局比赛中甲胜的局数,则????~????(3,0.6).甲最终获胜的概率为
????1=????(????=2)+????(????=3)=C32×0.62×0.4+C33×0.63=0.648.
采用5局3胜制,不妨设赛满5局,用????表示5局比赛中甲胜的局数,则????~????(5,0.6).甲最终获胜的概率为
????2=????(????=3)+????(????=4)+????(????=5)
=C53×0.63×0.42+C54×0.64×0.4+C55×0.65
=0.682?56.
因为????2>????1,所以5局3胜制对甲有利.实际上,比赛局数越多,对实力较强者越有利.
?
归纳总结:一般地,确定一个二项分布模型的步骤如下:
(1)明确伯努利试验及事件????的意义,确定事件????发生的概率????;
(2)确定重复试验的次数????,并判断各次试验的独立性;
(3)设????为????次独立重复试验中事件????发生的次数,则????~????(????,????).
?
探究:假设随机变量????服从二项分布????(????,????),那么????的均值和方差各是什么?
?
我们知道,抛掷一枚质地均匀的硬币,“正面朝上”的概率为0.5,如果掷100次硬币,期望有100×0.5=50次正面朝上.根据均值的含义,对于服从二项分布的随机变量????,我们猜想????(????)=????????.
我们不妨从简单开始,先考察????较小的情况.
(1)当????=1时,????服从两点分布,分布列为
????(????=0)=1?????,????(????=1)=????.
均值和方差分别为
????(????)=????,????(????)=????(1?????).
(2)当????=2时,????的分布列为
????(????=0)=(1?????)2,????(????=1)=2????(1?????),????(????=2)=????2.
均值和方差分别为
??????????(????)=0×(1?????)2+1×2????(1?????)+2×????2=2????.
??????(????)=02×(1?????)2+12×2????(1?????)+22×????2?(2????)2=2????(1?????).
?
一般地,可以证明:
如果????~????(????,????),那么????(????)=????????,????(????)=????????(1?????).
?
对均值的证明:
令????=1?????,由????C????????=C?????1?????1,可得
????(????)= ????C?????????????????????????????= C?????1?????1??????????????????????=???????? C?????1?????1?????????1?????????1?(?????1)?.
令?????1=????,则
????????=??????????????? C?????1?????????????????????1?????=????????????+?????????1=????????.
?
对方差的证明:
????????=?????(?????????(????))2 C????????????????1??????????????=????(????2?2????????????+(????????)2)C????????????????1???????????????
= ????2 C????????????????1????????????????2????????????????? C????????????????1???????????????+(????????)2???????C????????????????1???????????????
= ????2?C????????????????1????????????????2(????????)2+(????????)2= ????2 C????????????????1????????????????(????????)2,
又 ????2 C????????????????1???????????????=???(????(?????1)+????)?C????????????????1???????????????
= ?????????1C????????????????1??????????????+????????C????????????????1??????????????
=?????????1????2???????????2!?????2!?????2??????2!?????????21??????????2?(?????2)+????????
=?????????1????2?????C?????2????????????1??????????2?????+????????
=????(?????1)????2+????????,
因此????(????)=????(?????1)????2+?????????(????????)2=?????????????????2=????????(1?????).
?
随堂小测
1.有8件产品,其中4件是次品,从中有放回地取3次(每次1件),若????表示取得次品的次数,则????(????≤2)= ( )
A. 38 B. 1314 C. 45 D. 78
?
D
2.已知随机变量????+????=8,若????~????(10,0.4),则????(????),????(????)分别是( )
A.4和2.4 B.2和2.4 C.6和2.4 D.4和5.6
?
A
3.若随机变量????~????(????,????),且????(????)=52,????(????)=54,则????(????=1)= .(用数字作答)
?
532
?
4.某次考试共有12个选择题,每个选择题的分值为5分,每个选择题四个选项且只有一个选项是正确的,A学生对12个选择题中每个题的四个选项都没有把握,最后选择题的得分为????分,B学生对12个选择题中每个题的四个选项都能判断其中有一个选项是错误的,对其他三个选项都没有把握,最后选择题的得分为????分.则????(????)?????(????)的值为( )
A.12512 B.3512 C . 274 D.234
?
A
课堂小结
伯努利试验 与?????重伯努利试验
?
一般地,在????重伯努利试验中,设每次试验中事件????发生的概率为????(0?
二项分布
确定一个二项分布模型的步骤
(1)明确伯努利试验及事件????的意义,确定事件????发生的概率????;
(2)确定重复试验的次数????,并判断各次试验的独立性;
(3)设????为????次独立重复试验中事件????发生的次数,则????~????(????,????).
?
假设随机变量????服从二项分布????(????,????),那么
?
????(????)=????,????(????)=????(1?????).
?
二项分布的均值与方差
谢 谢!
