高中数学选择性必修第三册RJ·A--7.4 二项分布与超几何分布-7.4.2 超几何分布 课件(共16张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·A--7.4 二项分布与超几何分布-7.4.2 超几何分布 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览






文档简介
第七章
7.4
二项分布与超几何分布
7.4.2 超几何分布
学习目标
1. 通过具体实例,了解超几何分布及其均值,并能解决简单的实际问题.
核心素养:数学建模、逻辑推理、数学抽象、数学运算.
新知学习
问题:已知100件产品中有8件次品,分别采用有放回和不放回的方式随机抽取4件.设抽取的4件产品中次品数为????,求随机变量????的分布列.
我们知道,如果采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时????服从二项分布,即????~????(4,0.08).
?
思考:如果采用不放回抽样,那么抽取的4件产品中次品数????是否也服从二项分布?如果不服从,那么????的分布列是什么?
?
采用不放回抽样,虽然每次抽到次品的概率都是0.08,但每次抽取不是同一个试验,而且各次抽取的结果也不独立,不符合????重伯努利试验的特征,因此????不服从二项分布.
?
新知学习
问题:已知100件产品中有8件次品,分别采用有放回和不放回的方式随机抽取4件.设抽取的4件产品中次品数为????,求随机变量????的分布列.
我们知道,如果采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时????服从二项分布,即????~????(4,0.08).
?
思考:如果采用不放回抽样,那么抽取的4件产品中次品数????是否也服从二项分布?如果不服从,那么????的分布列是什么?
?
采用不放回抽样,虽然每次抽到次品的概率都是0.08,但每次抽取不是同一个试验,而且各次抽取的结果也不独立,不符合????重伯努利试验的特征,因此????不服从二项分布.
?
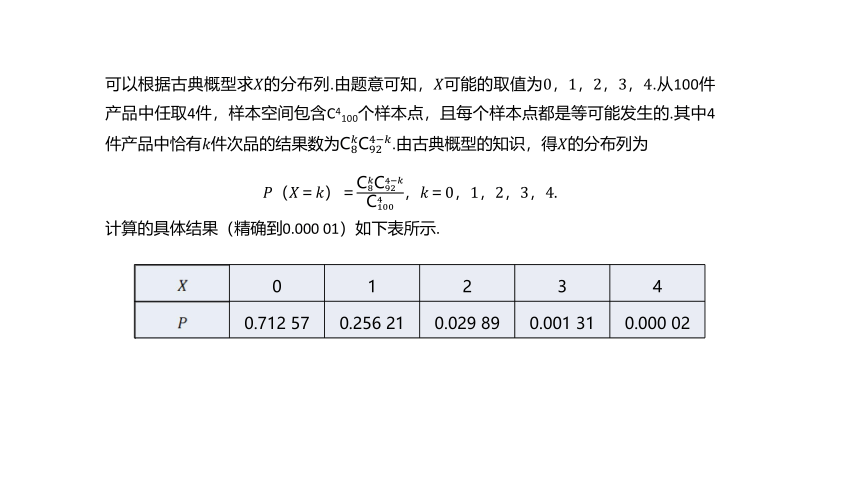
可以根据古典概型求????的分布列.由题意可知,????可能的取值为0,1,2,3,4.从100件产品中任取4件,样本空间包含C4100个样本点,且每个样本点都是等可能发生的.其中4件产品中恰有????件次品的结果数为C8????C924?????.由古典概型的知识,得????的分布列为
????(????=????)=C8????C924?????C1004,????=0,1,2,3,4.
计算的具体结果(精确到0.000 01)如下表所示.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
0
1
2
3
4
????
0.712 57
0.256 21
0.029 89
0.001 31
0.000 02
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
1
2
3
4
0.712 57
0.256 21
0.029 89
0.001 31
0.000 02
新知讲解
一般地,假设一批产品共有????件,其中有????件次品.从????件产品中随机抽取????件(不放回),用????表示抽取的????件产品中的次品数,则????的分布列为
????(????=????)=C????????C??????????????????C????????,????=????,????+1,????+2,…,????.
其中????,????,????∈?????,????≤????,????≤????,????=max?{0,?????????+????},????=min?{????,????}.如果随机变量????的分布列具有上式的形式,那么称随机变量????服从超几何分布.
?
典例剖析
例4?从50名学生中随机选出5名学生代表,求甲被选中的概率.
解:设????表示选出的5名学生中含甲的人数(只能取0或1),则????服从超几何
分布, 且????=50,????=1,????=5.因此甲被选中的概率为
????(????=1)=C11C494C505=110.
?
例5 一批零件共有30个,其中有3个不合格.随机抽取10个零件进行检测,求至少
有1件不合格的概率.
解:设抽取的10个零件中不合格品数为????,则????服从超几何分布,且????=30,????=3,
????=10.?????的分布列为
????(????=????)=C3????C2710?????C3010,????=0,1,2,3.
至少有1件不合格的概率为
????(????≥1)=????(????=1)+????(????=2)+????(????=3)
??????????? =C31C279C3010+C32C278C3010+C33C277C3010≈0.719?2.
也可以按如下方法求解:
????(????≥1)=1?????(????=0)=1?C30C2710C3010≈0.719?2.
?
探究:服从超几何分布的随机变量的均值是什么?
设随机变量????服从超几何分布,则????可以解释为从包含????件次品的????件产品中,不放回地随机抽取????件产品中的次品数.令????=????????,则????是????件产品的次品率,
而????????是抽取的????件产品的次品率,我们猜想????????????=????,即????(????)=????????.
实际上,由随机变量均值的定义,
令????=max?(0,?????????+????),????=min?(????,????),有
????????=????????C????????C??????????????????C????????=?????????C?????1?????1C??????????????????C????????.
因为 C?????1?????1C??????????????????=C?????1?????1,所以
????(????)=????C???????? C?????1?????1C???????????????????=????C?????1?????1C????????=????????????=????????.
?
例6?一个袋子中有100个大小相同的球,其中有40个黄球、60个白球,从中随机地摸出20个球作为样本.用X表示样本中黄球的个数.
(1)分别就有放回摸球和不放回摸球,求????的分布列;
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差不超过0.1的概率.
?
解:(1)对于有放回摸球,每次摸到黄球的概率为0.4,且各次试验之间的结果是独立的,因此????~????(20,0.4),????的分布列为
????1????=????(????=????)=C20????×0.4????×0.620??????,????=0,1,2,…,20.
对于不放回摸球,各次试验的结果不独立,????服从超几何分布,????的分布列为
????2????=????(????=????)=C40????C6020?????C10020,????=0,1,2,…,20.
?
(2)利用统计软件可以计算出两个分布列具体的概率值(精确到0.000 01),如下表所示.
k
p1k
p2k
?
k
p1k
p2k
0
0.000 04
0.000 01
11
0.070 99
0.063 76
1
0.000 49
0.000 15
12
0.035 50
0.026 67
2
0.003 09
0.001 35
13
0.014 56
0.008 67
3
0.012 35
0.007 14
14
0.004 85
0.002 17
4
0.034 99
0.025 51
15
0.001 29
0.000 41
5
0.074 65
0.065 30
16
0.000 27
0.000 06
6
0.124 41
0.124 22
17
0.000 04
0.000 01
7
0.165 88
0.179 72
18
0.000 00
0.000 00
8
0.179 71
0.200 78
19
0.000 00
0.000 00
9
0.159 74
0.174 83
20
0.000 00
0.000 00
10
0.117 14
0.119 24
?
?
?
样本中黄球的比例????20=????20是一个随机变量,根据表格,计算得
有放回摸球:????(|????20?0.4|≤0.1)
=????(6≤????≤10)≈0.746?9.
不放回摸球:????(|????20?0.4|≤0.1)
=????(6≤????≤10)≈0.798?8.
?
因此,在相同的误差限制下,采用不放回摸球估计的结果更可靠些.
两种摸球方式下,随机变量X分别服从二项分布和超几何分布.虽然这两种分布有相等的均值(都是8),但从两种分布的概率分布图(如下图)看,超几何分布更集中在均值附近.
二项分布和超几何分布都可以描述随机抽取的????件产品中次品数的分布规律,并且二者的均值相同.对于不放回抽样,当????远远小于????时,每抽取一次后,对????的影响很小,此时,超几何分布可以用二项分布近似.
?
随堂小测
1. 一个班级共有30名学生,其中有10名女生,现从中任选三人代表班级参加学校开展的某项活动,假设选出的3名代表中的女生人数为????,男生的人数为????,则????(????=2)+????(????=2)等于 ( )
?
C
2. 盒中有10个螺丝钉,其中有3个是坏的,现从盒中随机地抽取4个,那么概率是310的事件为 ( )
A.恰有1个是坏的 B.4个全是好的 C.恰有2个是好的 D.至多有2个是坏的
?
C
3.某学校实行自主招生,参加自主招生的学生从8个试题中随机挑选4个进行作答,至少答对3个才能通过初试.已知在这8个试题中甲能答对6个,则甲通过自主招生初试的概率为 ;记甲答对试题的个数为????,则????的数学期望????(????)= .
4. 从一批含有13个正品,2个次品的产品中,不放回地抽取3次,每次抽一个,设抽取的次品数为????,则????(5????+1)= .
?
1114
?
3
3
一般地,假设一批产品共有????件,其中有????件次品.从????件产品中随机抽取????件(不放回),用????表示抽取的????件产品中的次品数,则????的分布列为
????(????=????)=C????????C??????????????????C????????,????=????,????+1,????+2,…,????.
其中????,????,????∈?????,????≤????,????≤????,????=max?{0,?????????+????},????=min?{????,????}.如果随机变量????的分布列具有上式的形式,那么称随机变量????服从超几何分布.
?
课堂小结
超几何分布
????(????)=????????.
?
超几何分布的均值
谢 谢!
7.4
二项分布与超几何分布
7.4.2 超几何分布
学习目标
1. 通过具体实例,了解超几何分布及其均值,并能解决简单的实际问题.
核心素养:数学建模、逻辑推理、数学抽象、数学运算.
新知学习
问题:已知100件产品中有8件次品,分别采用有放回和不放回的方式随机抽取4件.设抽取的4件产品中次品数为????,求随机变量????的分布列.
我们知道,如果采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时????服从二项分布,即????~????(4,0.08).
?
思考:如果采用不放回抽样,那么抽取的4件产品中次品数????是否也服从二项分布?如果不服从,那么????的分布列是什么?
?
采用不放回抽样,虽然每次抽到次品的概率都是0.08,但每次抽取不是同一个试验,而且各次抽取的结果也不独立,不符合????重伯努利试验的特征,因此????不服从二项分布.
?
新知学习
问题:已知100件产品中有8件次品,分别采用有放回和不放回的方式随机抽取4件.设抽取的4件产品中次品数为????,求随机变量????的分布列.
我们知道,如果采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时????服从二项分布,即????~????(4,0.08).
?
思考:如果采用不放回抽样,那么抽取的4件产品中次品数????是否也服从二项分布?如果不服从,那么????的分布列是什么?
?
采用不放回抽样,虽然每次抽到次品的概率都是0.08,但每次抽取不是同一个试验,而且各次抽取的结果也不独立,不符合????重伯努利试验的特征,因此????不服从二项分布.
?
可以根据古典概型求????的分布列.由题意可知,????可能的取值为0,1,2,3,4.从100件产品中任取4件,样本空间包含C4100个样本点,且每个样本点都是等可能发生的.其中4件产品中恰有????件次品的结果数为C8????C924?????.由古典概型的知识,得????的分布列为
????(????=????)=C8????C924?????C1004,????=0,1,2,3,4.
计算的具体结果(精确到0.000 01)如下表所示.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}????
0
1
2
3
4
????
0.712 57
0.256 21
0.029 89
0.001 31
0.000 02
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
1
2
3
4
0.712 57
0.256 21
0.029 89
0.001 31
0.000 02
新知讲解
一般地,假设一批产品共有????件,其中有????件次品.从????件产品中随机抽取????件(不放回),用????表示抽取的????件产品中的次品数,则????的分布列为
????(????=????)=C????????C??????????????????C????????,????=????,????+1,????+2,…,????.
其中????,????,????∈?????,????≤????,????≤????,????=max?{0,?????????+????},????=min?{????,????}.如果随机变量????的分布列具有上式的形式,那么称随机变量????服从超几何分布.
?
典例剖析
例4?从50名学生中随机选出5名学生代表,求甲被选中的概率.
解:设????表示选出的5名学生中含甲的人数(只能取0或1),则????服从超几何
分布, 且????=50,????=1,????=5.因此甲被选中的概率为
????(????=1)=C11C494C505=110.
?
例5 一批零件共有30个,其中有3个不合格.随机抽取10个零件进行检测,求至少
有1件不合格的概率.
解:设抽取的10个零件中不合格品数为????,则????服从超几何分布,且????=30,????=3,
????=10.?????的分布列为
????(????=????)=C3????C2710?????C3010,????=0,1,2,3.
至少有1件不合格的概率为
????(????≥1)=????(????=1)+????(????=2)+????(????=3)
??????????? =C31C279C3010+C32C278C3010+C33C277C3010≈0.719?2.
也可以按如下方法求解:
????(????≥1)=1?????(????=0)=1?C30C2710C3010≈0.719?2.
?
探究:服从超几何分布的随机变量的均值是什么?
设随机变量????服从超几何分布,则????可以解释为从包含????件次品的????件产品中,不放回地随机抽取????件产品中的次品数.令????=????????,则????是????件产品的次品率,
而????????是抽取的????件产品的次品率,我们猜想????????????=????,即????(????)=????????.
实际上,由随机变量均值的定义,
令????=max?(0,?????????+????),????=min?(????,????),有
????????=????????C????????C??????????????????C????????=?????????C?????1?????1C??????????????????C????????.
因为 C?????1?????1C??????????????????=C?????1?????1,所以
????(????)=????C???????? C?????1?????1C???????????????????=????C?????1?????1C????????=????????????=????????.
?
例6?一个袋子中有100个大小相同的球,其中有40个黄球、60个白球,从中随机地摸出20个球作为样本.用X表示样本中黄球的个数.
(1)分别就有放回摸球和不放回摸球,求????的分布列;
(2)分别就有放回摸球和不放回摸球,用样本中黄球的比例估计总体中黄球的比例,求误差不超过0.1的概率.
?
解:(1)对于有放回摸球,每次摸到黄球的概率为0.4,且各次试验之间的结果是独立的,因此????~????(20,0.4),????的分布列为
????1????=????(????=????)=C20????×0.4????×0.620??????,????=0,1,2,…,20.
对于不放回摸球,各次试验的结果不独立,????服从超几何分布,????的分布列为
????2????=????(????=????)=C40????C6020?????C10020,????=0,1,2,…,20.
?
(2)利用统计软件可以计算出两个分布列具体的概率值(精确到0.000 01),如下表所示.
k
p1k
p2k
?
k
p1k
p2k
0
0.000 04
0.000 01
11
0.070 99
0.063 76
1
0.000 49
0.000 15
12
0.035 50
0.026 67
2
0.003 09
0.001 35
13
0.014 56
0.008 67
3
0.012 35
0.007 14
14
0.004 85
0.002 17
4
0.034 99
0.025 51
15
0.001 29
0.000 41
5
0.074 65
0.065 30
16
0.000 27
0.000 06
6
0.124 41
0.124 22
17
0.000 04
0.000 01
7
0.165 88
0.179 72
18
0.000 00
0.000 00
8
0.179 71
0.200 78
19
0.000 00
0.000 00
9
0.159 74
0.174 83
20
0.000 00
0.000 00
10
0.117 14
0.119 24
?
?
?
样本中黄球的比例????20=????20是一个随机变量,根据表格,计算得
有放回摸球:????(|????20?0.4|≤0.1)
=????(6≤????≤10)≈0.746?9.
不放回摸球:????(|????20?0.4|≤0.1)
=????(6≤????≤10)≈0.798?8.
?
因此,在相同的误差限制下,采用不放回摸球估计的结果更可靠些.
两种摸球方式下,随机变量X分别服从二项分布和超几何分布.虽然这两种分布有相等的均值(都是8),但从两种分布的概率分布图(如下图)看,超几何分布更集中在均值附近.
二项分布和超几何分布都可以描述随机抽取的????件产品中次品数的分布规律,并且二者的均值相同.对于不放回抽样,当????远远小于????时,每抽取一次后,对????的影响很小,此时,超几何分布可以用二项分布近似.
?
随堂小测
1. 一个班级共有30名学生,其中有10名女生,现从中任选三人代表班级参加学校开展的某项活动,假设选出的3名代表中的女生人数为????,男生的人数为????,则????(????=2)+????(????=2)等于 ( )
?
C
2. 盒中有10个螺丝钉,其中有3个是坏的,现从盒中随机地抽取4个,那么概率是310的事件为 ( )
A.恰有1个是坏的 B.4个全是好的 C.恰有2个是好的 D.至多有2个是坏的
?
C
3.某学校实行自主招生,参加自主招生的学生从8个试题中随机挑选4个进行作答,至少答对3个才能通过初试.已知在这8个试题中甲能答对6个,则甲通过自主招生初试的概率为 ;记甲答对试题的个数为????,则????的数学期望????(????)= .
4. 从一批含有13个正品,2个次品的产品中,不放回地抽取3次,每次抽一个,设抽取的次品数为????,则????(5????+1)= .
?
1114
?
3
3
一般地,假设一批产品共有????件,其中有????件次品.从????件产品中随机抽取????件(不放回),用????表示抽取的????件产品中的次品数,则????的分布列为
????(????=????)=C????????C??????????????????C????????,????=????,????+1,????+2,…,????.
其中????,????,????∈?????,????≤????,????≤????,????=max?{0,?????????+????},????=min?{????,????}.如果随机变量????的分布列具有上式的形式,那么称随机变量????服从超几何分布.
?
课堂小结
超几何分布
????(????)=????????.
?
超几何分布的均值
谢 谢!
