高中数学选择性必修第三册RJ·A--8.1 成对数据的统计相关性 课件(共30张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·A--8.1 成对数据的统计相关性 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览







文档简介
第八章
8.1
成对数据的统计相关性
学习目标
1.会画出成对样本数据的散点图.
2.会通过散点图判断成对样本数据的相关性.
3.结合实例,了解样本相关系数的统计含义,了解样本相关系数与“标准化”处理后的成对数据两分量向量夹角的关系.
4.结合实例,会通过相关系数比较多组成对数据的相关性.
核心素养:数据分析、数学运算、逻辑推理、数学抽象.
新知学习
我们知道,如果变量y是变量x的函数,那么由????就可以唯一确定????.然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度.例如,人的体重与身高存在关系,但由一个人的身高值并不能确定他的体重值.那么,该如何刻画这两个变量之间的关系呢?下面我们就来研究这个问题.
?
新知学习
我们知道,如果变量y是变量x的函数,那么由????就可以唯一确定????.然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度.例如,人的体重与身高存在关系,但由一个人的身高值并不能确定他的体重值.那么,该如何刻画这两个变量之间的关系呢?下面我们就来研究这个问题.
?
我们知道,一个人的体重与他的身高有关系.一般而言,个子高的人往往体重值较大,个子矮的人往往体重值较小.但身高并不是决定体重的唯一因素,例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素.像这样,两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
现实中两个变量具有相关关系的事例:
1.子女身高????与父亲身高????之间的关系.一般来说,父亲的个子高,其子女的个子也会比较高;父亲个子矮,其子女的个子也会比较矮.但影响子女身高的因素,除父亲身高外还有其他因素,例如母亲身高、饮食结构、体育锻炼等,因此父亲身高又不能完全决定子女身高.
2.商品销售收入????与广告支出????之间的关系.一般来说,广告支出越多,商品销售收入越高.但广告支出并不是决定商品销售收入的唯一因素,商品销售收入还与商品质量、居民收入等因素有关.
3.空气污染指数????与汽车保有量????之间的关系.一般来说,汽车保有量增加,空气污染指数会上升.但汽车保有量并不是造成空气污染的唯一因素,气象条件、工业生产排放、居民生活和取暖、垃圾焚烧等都是影响空气污染指数的因素.
4.粮食亩产量????与施肥量????之间的关系.在一定范围内,施肥量越大,粮食亩产量就越高.但施肥量并不是决定粮食亩产量的唯一因素,粮食亩产量还要受到土壤质量、降水量、田间管理水平等因素的影响.
?
因为在相关关系中,变量????的值不能随变量?????的值的确定而唯一确定,所以我们无法直接用函数去描述变量之间的这种关系.对上述各例中两个变量之间的相关关系,我们往往会根据自己以往积累的经验作出推断.“经验之中有规律”,经验的确可以为我们的决策提供一定的依据,但仅凭经验推断又有不足.例如,不同经验的人对同一情形可能会得出不同结论,不是所有的情形都有经验可循等.因此,在研究两个变量之间的相关关系时,我们需要借助数据说话,即通过样本数据分析,从数据中提取信息,并构建适当的模型,再利用模型进行估计或推断.
?
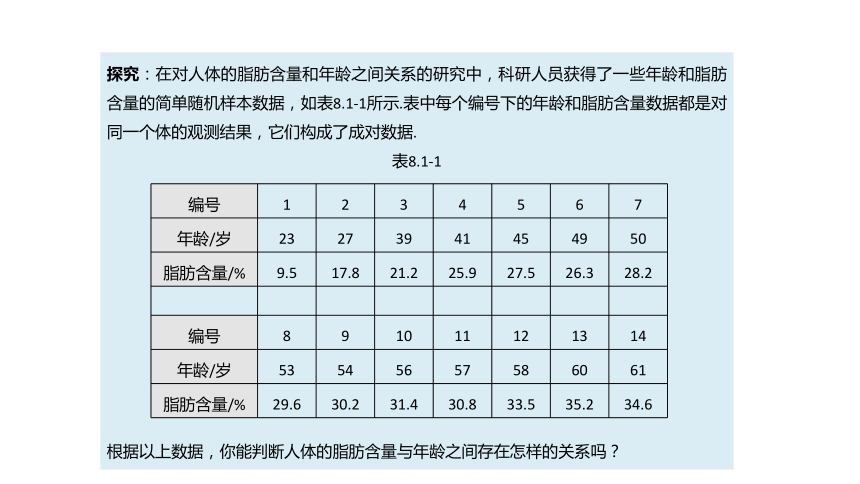
探究:在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表8.1-1所示.表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.
表8.1-1
?
根据以上数据,你能判断人体的脂肪含量与年龄之间存在怎样的关系吗?
编号
1
2
3
4
5
6
7
年龄/岁
23
27
39
41
45
49
50
脂肪含量/%
9.5
17.8
21.2
25.9
27.5
26.3
28.2
?
?
?
?
?
?
?
?
编号
8
9
10
11
12
13
14
年龄/岁
53
54
56
57
58
60
61
脂肪含量/%
29.6
30.2
31.4
30.8
33.5
35.2
34.6
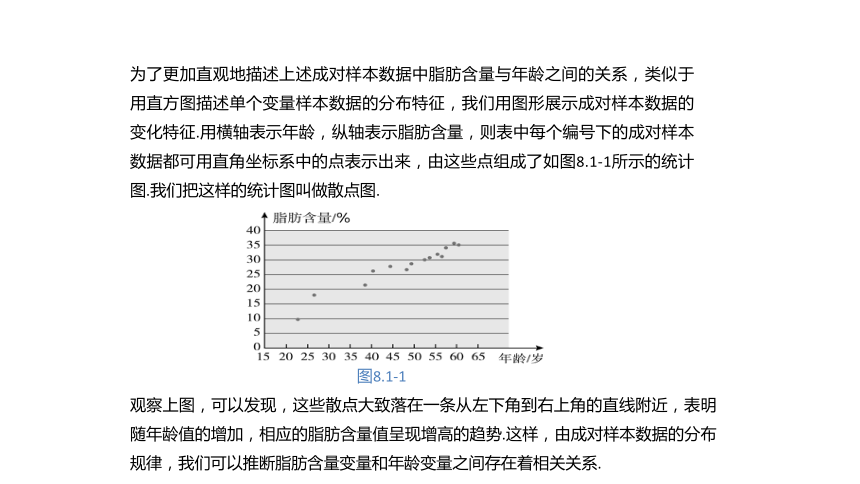
为了更加直观地描述上述成对样本数据中脂肪含量与年龄之间的关系,类似于用直方图描述单个变量样本数据的分布特征,我们用图形展示成对样本数据的变化特征.用横轴表示年龄,纵轴表示脂肪含量,则表中每个编号下的成对样本数据都可用直角坐标系中的点表示出来,由这些点组成了如图8.1-1所示的统计图.我们把这样的统计图叫做散点图.
观察上图,可以发现,这些散点大致落在一条从左下角到右上角的直线附近,表明随年龄值的增加,相应的脂肪含量值呈现增高的趋势.这样,由成对样本数据的分布规律,我们可以推断脂肪含量变量和年龄变量之间存在着相关关系.
图8.1-1
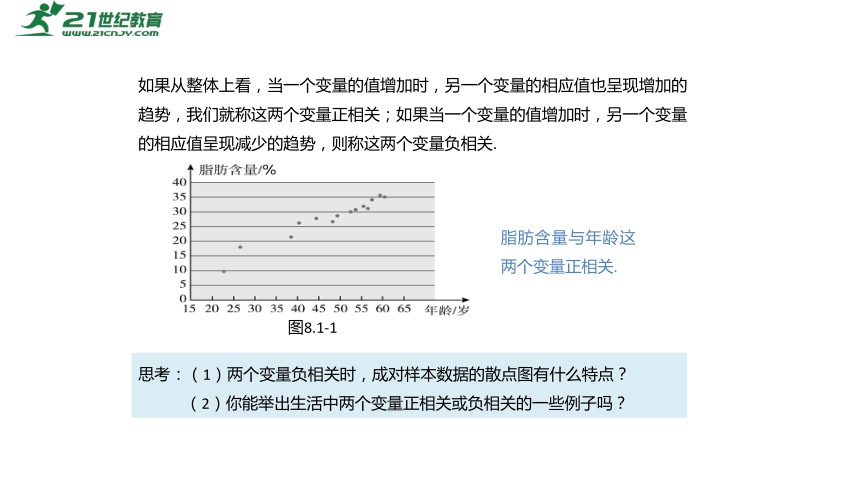
如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关;如果当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关.
脂肪含量与年龄这两个变量正相关.
思考:(1)两个变量负相关时,成对样本数据的散点图有什么特点?
(2)你能举出生活中两个变量正相关或负相关的一些例子吗?
图8.1-1
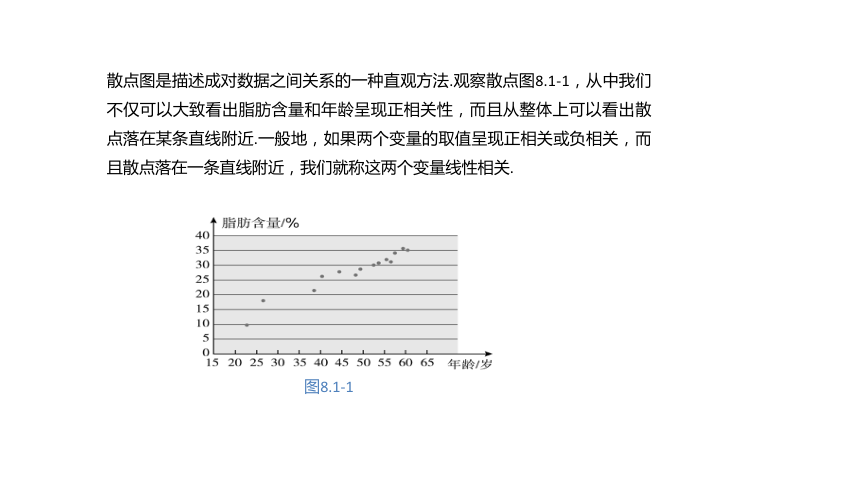
散点图是描述成对数据之间关系的一种直观方法.观察散点图8.1-1,从中我们不仅可以大致看出脂肪含量和年龄呈现正相关性,而且从整体上可以看出散点落在某条直线附近.一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关.
图8.1-1
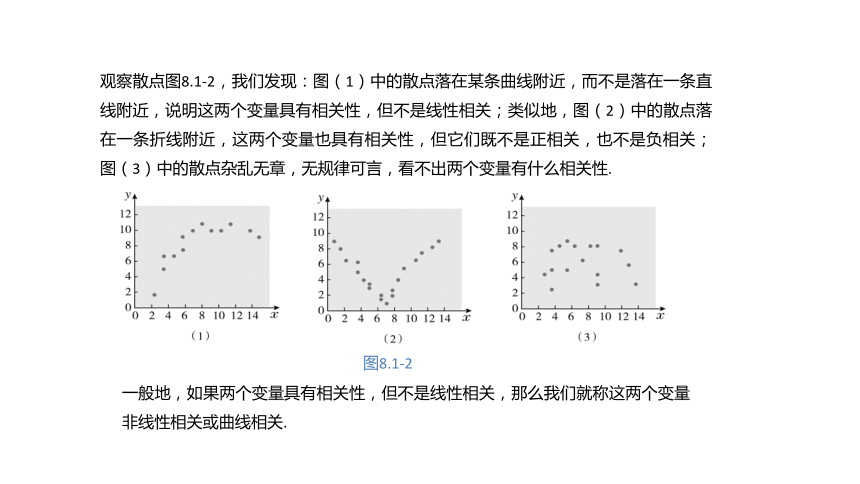
观察散点图8.1-2,我们发现:图(1)中的散点落在某条曲线附近,而不是落在一条直线附近,说明这两个变量具有相关性,但不是线性相关;类似地,图(2)中的散点落在一条折线附近,这两个变量也具有相关性,但它们既不是正相关,也不是负相关;图(3)中的散点杂乱无章,无规律可言,看不出两个变量有什么相关性.
一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
图8.1-2
通过观察散点图中成对样本数据的分布规律,我们可以大致推断两个变量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关等.散点图虽然直观,但无法确切地反映成对样本数据的相关程度,也就无法量化两个变量之间相关程度的大小.能否像引入平均值、方差等数字特征对单个变量数据进行分析那样,引入一个适当的“数字特征”,对成对样本数据的相关程度进行定量分析呢?
对于变量????和变量????,设经过随机抽样获得的成对样本数据为(????1,????1),(????2,????2),…,(????????,????????),其中????1,????2,…,????????和????1,????2,…,????????的均值分别为????和?????.将数据以(????,????)为零点进行平移,得到平移后的成对数据为(????1?????,????1?????),(????2?????,????2?????),…,(?????????????,?????????????),
并绘制散点图.
?
利用上述方法处理表8.1-1中的数据,得到图8.1-3.我们发现,这时的散点大多数分布在第一象限、第三象限,大多数散点的横、纵坐标同号.显然,这样的规律是由人体脂肪含量与年龄正相关所决定的.
图8.1-3
一般地,如果变量x和y正相关,那么关于均值平移后的大多数散点将分布在第一象限、第三象限,对应的成对数据同号的居多,如图8.1-4(1)所示;如果变量x和y负相关,那么关于均值平移后的大多数散点将分布在第二象限、第四象限,对应的成对数据异号的居多,如图8.1-4(2)所示.
图8.1-4
(1) (2)
思考:根据上述分析,你能利用正相关变量和负相关变量的成对样本数据平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数字特征吗?
从上述讨论得到启发,利用散点(?????????????,?????????????)(????=1,2,…,????)的横、纵坐标是否同号,可以构造一个量
????????????=1????[(????1?????)(????1?????)+(????2?????)(????2?????)+…+(?????????????)(?????????????)].
一般情形下,????????????>0表明成对样本数据正相关;????????????<0表明成对样本数据负相关.
?
思考:你认为????????????的大小一定能度量出成对样本数据的相关程度吗?
?
因为????????????的大小与数据的度量单位有关,所以不宜直接用它度量成对样本数据相关程度的大小.例如,在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高的单位由米改为厘米,则相应的????????????将变为原来的100倍,但单位的改变并不会导致体重与身高之间相关程度的改变.
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.我们用
分别除????????????? 和?????????????(????=1,2,…,????),得
????1?????????????,????1?????????????,????2?????????????,????2?????????????,…,?????????????????????,?????????????????????.
为简单起见,把上述“标准化”处理后的成对数据分别记为
(????′1,????′1),(????′2,????′2),…,(????′????,????′????),
?
仿照????????????的构造,可以得到
我们称????为变量????和变量????的样本相关系数
?
变形形式
当????>0时,称成对样本数据正相关.这时,当其中一个数据的值变小时,另一个数据的值通常也变小;当其中一个数据的值变大时,另一个数据的值通常也变大.
当????<0时,称成对样本数据负相关.这时,当其中一个数据的值变小时,另一个数据的值通常会变大;当其中一个数据的值变大时,另一个数据的值通常会变小.
?
探究:样本相关系数????的大小与成对样本数据的相关程度有什么内在联系呢?
?
观察????的结构,联想到二维(平面)向量、三维(空间)向量数量积的坐标表示,我们将向量的维数推广到????维,????维向量????,????的数量积仍然定义为
????·????=|????||????|cos?????,
其中????为向量????,????的夹角.类似于平面或空间向量的坐标表示,对于向量????=(????1,????2,…,????????)和????=(????1,????2,…,????????),我们有
????·????=????1????1+????2????2+…+????????????????.
设“标准化”处理后的成对数据(????′1,????′1),(????′2,????′2),…,(????′????,????′????)的第一分量构成????维向量????′=(????′1,????′2,…,????′????),
第二分量构成????维向量????′=(????′1,????′2,…,????′????),
则有????=1????????′·????′=1????|????′||????′|cos?????.
因为|????′|=|????′|=????,所以样本相关系数????=cos?????,其中????为向量????′和向量????′的夹角.
由?1≤cos?????≤1,可知?1≤????≤1.
?
思考:当|????|=1时,成对样本数据之间具有怎样的关系呢?
?
当|????|=1时,????=cos?????中的????=0或π,向量????′和????′共线.由向量的知识可知,存在实数????,使得????′=????????′,即
?????????????????????=?????????????????????????,????=1,2,…,????.
这表明成对样本数据(????????,????????)都落在直线?????????=????????????????????(?????????)上.
这时,成对样本数据的两个分量之间满足一种线性关系.
由此可见,样本相关系数????的取值范围为[?1,1].样本相关系数????的绝对值大小可以反映成对样本数据之间线性相关的程度:
当|????|越接近1时,成对样本数据的线性相关程度越强;
当|????|越接近0时,成对样本数据的线性相关程度越弱.
?
图8.1-5是不同成对样本数据的散点图和相应的样本相关系数.图(1)中的散点有明显的从左下角到右上角沿直线分布的趋势,说明成对样本数据呈现出线性相关关系;样本相关系数????=0.97,表明成对样本数据的正线性相关程度很强.图(2)中的散点有明显的从左上角到右下角沿直线分布的趋势,说明成对样本数据也呈现出线性相关关系;样本相关系数????=?0.85,表明成对样本数据的负线性相关程度比较强.从样本相关系数来看,图(1)中成对样本数据的线性相关程度要比图(2)中强一些;图(3)和图(4)中的成对样本数据的线性相关程度很弱,其中图(4)中成对样本数据的线性相关程度极弱.
?
图8.1-5
综上可知,两个随机变量的相关性可以通过成对样本数据进行分析,而样本相关系数????可以反映两个随机变量之间的线性相关程度:????的符号反映了相关关系的正负性;|????|的大小反映了两个变量线性相关的程度,即散点集中于一条直线的程度.
在有限总体中,若要确切地了解两个变量之间相关关系的正负性及线性相关的程度,我们可以利用这两个变量取值的所有成对数据,通过公式(1)就可以计算出两个变量的相关系数.例如,要确切了解脂肪含量????与年龄????的线性相关程度,需要调查所有人的年龄及其脂肪含量,再将得到的成对数据代入公式(1),计算出相关系数.这个相关系数就能确切地反映变量之间的相关程度.
?
典例剖析
例1 根据表8.1-1中脂肪含量和年龄的样本数据,推断两个变量是否线性相关,计算样本
相关系数,并推断它们的相关程度.
编号
1
2
3
4
5
6
7
年龄/岁
23
27
39
41
45
49
50
脂肪含量/%
9.5
17.8
21.2
25.9
27.5
26.3
28.2
?
?
?
?
?
?
?
?
编号
8
9
10
11
12
13
14
年龄/岁
53
54
56
57
58
60
61
脂肪含量/%
29.6
30.2
31.4
30.8
33.5
35.2
34.6
表8.1-1
解:先画出散点图,如图8.1-1所示.观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
根据样本相关系数的定义,
图8.1-1
利用计算工具计算可得
代入①式,得????≈19?403.2?14×48.07×27.2634??181?14×48.072×11??051.77?14×27.262≈0.97.
由样本相关系数????≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
?
例2 有人收集了某城市居民年收入(即所有居民在一年内收入的总和)与A商品销售额的
10年数据,如表8.1-2所示.
第????年
1
2
3
4
5
6
7
8
9
10
居民年收入/亿元
32.2
31.1
32.9
35.8
37.1
38.0
39.0
43.0
44.6
46.0
A商品销售额/万元
25.0
30.0
34.0
37.0
39.0
41.0
42.0
44.0
48.0
51.0
1
2
3
4
5
6
7
8
9
10
居民年收入/亿元
32.2
31.1
32.9
35.8
37.1
38.0
39.0
43.0
44.6
46.0
A商品销售额/万元
25.0
30.0
34.0
37.0
39.0
41.0
42.0
44.0
48.0
51.0
表8.1-2
画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
解:画出成对样本数据的散点图,如图8.1-6所示.从散点图看,A商品销售额与居民年收入的样本数据呈现出线性相关关系.
由样本数据计算得样本相关系数r≈0.95.由此可以推断,A商品销售额与居民年收入正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强.
图8.1-6
例3 在某校高一年级中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如表8.1-3所示.
编号
身高/cm
体重/kg
臂展/cm
?
编号
身高/cm
体重/kg
臂展/cm
1
2
3
4
5
6
7
8
9
10
11
12
13
173
179
175
179
182
173
180
170
169
177
177
178
174
55
71
52
62
82
63
55
81
54
54
59
67
56
169
170
172
177
174
166
174
169
166
176
170
174
170
14
15
16
17
18
19
20
21
22
23
24
25
?
166
176
176
175
169
184
169
182
171
177
173
173
?
66
61
49
60
48
86
58
54
58
61
58
51
?
161
166
165
173
162
189
164
170
164
173
165
169
?
体重与身高、臂展与身高分别具有怎样的相关性?
解:根据样本数据分别画出体重与身高、臂展与身高的散点图,分别如图8.1-7(1)和(2)所示,两个散点图都呈现出线性相关的特征.
图8.1-7
(1) (2)
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,都为正线性相关.其中,臂展与身高的相关程度更高.
随堂小测
【解】(方法一)根据实际生活的经验可知,人的身高和体重之间存在相关关系.
(方法二)观察表格中的数据可知,人的体重随着身高的增高而增长,因此人的身高和体重之间存在相关关系.
(方法三)以????轴表示身高,以????轴表示体重,得到相应的散点图如图所示.我们会发现,随着身高的增高,体重基本上呈增长的趋势.所以体重与身高之间存在相关关系,并且是正相关.
?
2.对四组数据进行统计,获得如图所示的散点图,关于其相关系数的比较,正确的是( )
A.????2 C.????4?
A
相关系数为????1 相关系数为????2?????????????????????????????????????相关系数为????3 相关系数为????4
(1) (2) (3) (4)
?
课堂小结
变量的相关关系
散点图
样本相关系数
正相关、负相关
线性相关、非线性相关
谢 谢!
8.1
成对数据的统计相关性
学习目标
1.会画出成对样本数据的散点图.
2.会通过散点图判断成对样本数据的相关性.
3.结合实例,了解样本相关系数的统计含义,了解样本相关系数与“标准化”处理后的成对数据两分量向量夹角的关系.
4.结合实例,会通过相关系数比较多组成对数据的相关性.
核心素养:数据分析、数学运算、逻辑推理、数学抽象.
新知学习
我们知道,如果变量y是变量x的函数,那么由????就可以唯一确定????.然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度.例如,人的体重与身高存在关系,但由一个人的身高值并不能确定他的体重值.那么,该如何刻画这两个变量之间的关系呢?下面我们就来研究这个问题.
?
新知学习
我们知道,如果变量y是变量x的函数,那么由????就可以唯一确定????.然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度.例如,人的体重与身高存在关系,但由一个人的身高值并不能确定他的体重值.那么,该如何刻画这两个变量之间的关系呢?下面我们就来研究这个问题.
?
我们知道,一个人的体重与他的身高有关系.一般而言,个子高的人往往体重值较大,个子矮的人往往体重值较小.但身高并不是决定体重的唯一因素,例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素.像这样,两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
现实中两个变量具有相关关系的事例:
1.子女身高????与父亲身高????之间的关系.一般来说,父亲的个子高,其子女的个子也会比较高;父亲个子矮,其子女的个子也会比较矮.但影响子女身高的因素,除父亲身高外还有其他因素,例如母亲身高、饮食结构、体育锻炼等,因此父亲身高又不能完全决定子女身高.
2.商品销售收入????与广告支出????之间的关系.一般来说,广告支出越多,商品销售收入越高.但广告支出并不是决定商品销售收入的唯一因素,商品销售收入还与商品质量、居民收入等因素有关.
3.空气污染指数????与汽车保有量????之间的关系.一般来说,汽车保有量增加,空气污染指数会上升.但汽车保有量并不是造成空气污染的唯一因素,气象条件、工业生产排放、居民生活和取暖、垃圾焚烧等都是影响空气污染指数的因素.
4.粮食亩产量????与施肥量????之间的关系.在一定范围内,施肥量越大,粮食亩产量就越高.但施肥量并不是决定粮食亩产量的唯一因素,粮食亩产量还要受到土壤质量、降水量、田间管理水平等因素的影响.
?
因为在相关关系中,变量????的值不能随变量?????的值的确定而唯一确定,所以我们无法直接用函数去描述变量之间的这种关系.对上述各例中两个变量之间的相关关系,我们往往会根据自己以往积累的经验作出推断.“经验之中有规律”,经验的确可以为我们的决策提供一定的依据,但仅凭经验推断又有不足.例如,不同经验的人对同一情形可能会得出不同结论,不是所有的情形都有经验可循等.因此,在研究两个变量之间的相关关系时,我们需要借助数据说话,即通过样本数据分析,从数据中提取信息,并构建适当的模型,再利用模型进行估计或推断.
?
探究:在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表8.1-1所示.表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.
表8.1-1
?
根据以上数据,你能判断人体的脂肪含量与年龄之间存在怎样的关系吗?
编号
1
2
3
4
5
6
7
年龄/岁
23
27
39
41
45
49
50
脂肪含量/%
9.5
17.8
21.2
25.9
27.5
26.3
28.2
?
?
?
?
?
?
?
?
编号
8
9
10
11
12
13
14
年龄/岁
53
54
56
57
58
60
61
脂肪含量/%
29.6
30.2
31.4
30.8
33.5
35.2
34.6
为了更加直观地描述上述成对样本数据中脂肪含量与年龄之间的关系,类似于用直方图描述单个变量样本数据的分布特征,我们用图形展示成对样本数据的变化特征.用横轴表示年龄,纵轴表示脂肪含量,则表中每个编号下的成对样本数据都可用直角坐标系中的点表示出来,由这些点组成了如图8.1-1所示的统计图.我们把这样的统计图叫做散点图.
观察上图,可以发现,这些散点大致落在一条从左下角到右上角的直线附近,表明随年龄值的增加,相应的脂肪含量值呈现增高的趋势.这样,由成对样本数据的分布规律,我们可以推断脂肪含量变量和年龄变量之间存在着相关关系.
图8.1-1
如果从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关;如果当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关.
脂肪含量与年龄这两个变量正相关.
思考:(1)两个变量负相关时,成对样本数据的散点图有什么特点?
(2)你能举出生活中两个变量正相关或负相关的一些例子吗?
图8.1-1
散点图是描述成对数据之间关系的一种直观方法.观察散点图8.1-1,从中我们不仅可以大致看出脂肪含量和年龄呈现正相关性,而且从整体上可以看出散点落在某条直线附近.一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关.
图8.1-1
观察散点图8.1-2,我们发现:图(1)中的散点落在某条曲线附近,而不是落在一条直线附近,说明这两个变量具有相关性,但不是线性相关;类似地,图(2)中的散点落在一条折线附近,这两个变量也具有相关性,但它们既不是正相关,也不是负相关;图(3)中的散点杂乱无章,无规律可言,看不出两个变量有什么相关性.
一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
图8.1-2
通过观察散点图中成对样本数据的分布规律,我们可以大致推断两个变量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关等.散点图虽然直观,但无法确切地反映成对样本数据的相关程度,也就无法量化两个变量之间相关程度的大小.能否像引入平均值、方差等数字特征对单个变量数据进行分析那样,引入一个适当的“数字特征”,对成对样本数据的相关程度进行定量分析呢?
对于变量????和变量????,设经过随机抽样获得的成对样本数据为(????1,????1),(????2,????2),…,(????????,????????),其中????1,????2,…,????????和????1,????2,…,????????的均值分别为????和?????.将数据以(????,????)为零点进行平移,得到平移后的成对数据为(????1?????,????1?????),(????2?????,????2?????),…,(?????????????,?????????????),
并绘制散点图.
?
利用上述方法处理表8.1-1中的数据,得到图8.1-3.我们发现,这时的散点大多数分布在第一象限、第三象限,大多数散点的横、纵坐标同号.显然,这样的规律是由人体脂肪含量与年龄正相关所决定的.
图8.1-3
一般地,如果变量x和y正相关,那么关于均值平移后的大多数散点将分布在第一象限、第三象限,对应的成对数据同号的居多,如图8.1-4(1)所示;如果变量x和y负相关,那么关于均值平移后的大多数散点将分布在第二象限、第四象限,对应的成对数据异号的居多,如图8.1-4(2)所示.
图8.1-4
(1) (2)
思考:根据上述分析,你能利用正相关变量和负相关变量的成对样本数据平移后呈现的规律,构造一个度量成对样本数据是正相关还是负相关的数字特征吗?
从上述讨论得到启发,利用散点(?????????????,?????????????)(????=1,2,…,????)的横、纵坐标是否同号,可以构造一个量
????????????=1????[(????1?????)(????1?????)+(????2?????)(????2?????)+…+(?????????????)(?????????????)].
一般情形下,????????????>0表明成对样本数据正相关;????????????<0表明成对样本数据负相关.
?
思考:你认为????????????的大小一定能度量出成对样本数据的相关程度吗?
?
因为????????????的大小与数据的度量单位有关,所以不宜直接用它度量成对样本数据相关程度的大小.例如,在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高的单位由米改为厘米,则相应的????????????将变为原来的100倍,但单位的改变并不会导致体重与身高之间相关程度的改变.
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.我们用
分别除????????????? 和?????????????(????=1,2,…,????),得
????1?????????????,????1?????????????,????2?????????????,????2?????????????,…,?????????????????????,?????????????????????.
为简单起见,把上述“标准化”处理后的成对数据分别记为
(????′1,????′1),(????′2,????′2),…,(????′????,????′????),
?
仿照????????????的构造,可以得到
我们称????为变量????和变量????的样本相关系数
?
变形形式
当????>0时,称成对样本数据正相关.这时,当其中一个数据的值变小时,另一个数据的值通常也变小;当其中一个数据的值变大时,另一个数据的值通常也变大.
当????<0时,称成对样本数据负相关.这时,当其中一个数据的值变小时,另一个数据的值通常会变大;当其中一个数据的值变大时,另一个数据的值通常会变小.
?
探究:样本相关系数????的大小与成对样本数据的相关程度有什么内在联系呢?
?
观察????的结构,联想到二维(平面)向量、三维(空间)向量数量积的坐标表示,我们将向量的维数推广到????维,????维向量????,????的数量积仍然定义为
????·????=|????||????|cos?????,
其中????为向量????,????的夹角.类似于平面或空间向量的坐标表示,对于向量????=(????1,????2,…,????????)和????=(????1,????2,…,????????),我们有
????·????=????1????1+????2????2+…+????????????????.
设“标准化”处理后的成对数据(????′1,????′1),(????′2,????′2),…,(????′????,????′????)的第一分量构成????维向量????′=(????′1,????′2,…,????′????),
第二分量构成????维向量????′=(????′1,????′2,…,????′????),
则有????=1????????′·????′=1????|????′||????′|cos?????.
因为|????′|=|????′|=????,所以样本相关系数????=cos?????,其中????为向量????′和向量????′的夹角.
由?1≤cos?????≤1,可知?1≤????≤1.
?
思考:当|????|=1时,成对样本数据之间具有怎样的关系呢?
?
当|????|=1时,????=cos?????中的????=0或π,向量????′和????′共线.由向量的知识可知,存在实数????,使得????′=????????′,即
?????????????????????=?????????????????????????,????=1,2,…,????.
这表明成对样本数据(????????,????????)都落在直线?????????=????????????????????(?????????)上.
这时,成对样本数据的两个分量之间满足一种线性关系.
由此可见,样本相关系数????的取值范围为[?1,1].样本相关系数????的绝对值大小可以反映成对样本数据之间线性相关的程度:
当|????|越接近1时,成对样本数据的线性相关程度越强;
当|????|越接近0时,成对样本数据的线性相关程度越弱.
?
图8.1-5是不同成对样本数据的散点图和相应的样本相关系数.图(1)中的散点有明显的从左下角到右上角沿直线分布的趋势,说明成对样本数据呈现出线性相关关系;样本相关系数????=0.97,表明成对样本数据的正线性相关程度很强.图(2)中的散点有明显的从左上角到右下角沿直线分布的趋势,说明成对样本数据也呈现出线性相关关系;样本相关系数????=?0.85,表明成对样本数据的负线性相关程度比较强.从样本相关系数来看,图(1)中成对样本数据的线性相关程度要比图(2)中强一些;图(3)和图(4)中的成对样本数据的线性相关程度很弱,其中图(4)中成对样本数据的线性相关程度极弱.
?
图8.1-5
综上可知,两个随机变量的相关性可以通过成对样本数据进行分析,而样本相关系数????可以反映两个随机变量之间的线性相关程度:????的符号反映了相关关系的正负性;|????|的大小反映了两个变量线性相关的程度,即散点集中于一条直线的程度.
在有限总体中,若要确切地了解两个变量之间相关关系的正负性及线性相关的程度,我们可以利用这两个变量取值的所有成对数据,通过公式(1)就可以计算出两个变量的相关系数.例如,要确切了解脂肪含量????与年龄????的线性相关程度,需要调查所有人的年龄及其脂肪含量,再将得到的成对数据代入公式(1),计算出相关系数.这个相关系数就能确切地反映变量之间的相关程度.
?
典例剖析
例1 根据表8.1-1中脂肪含量和年龄的样本数据,推断两个变量是否线性相关,计算样本
相关系数,并推断它们的相关程度.
编号
1
2
3
4
5
6
7
年龄/岁
23
27
39
41
45
49
50
脂肪含量/%
9.5
17.8
21.2
25.9
27.5
26.3
28.2
?
?
?
?
?
?
?
?
编号
8
9
10
11
12
13
14
年龄/岁
53
54
56
57
58
60
61
脂肪含量/%
29.6
30.2
31.4
30.8
33.5
35.2
34.6
表8.1-1
解:先画出散点图,如图8.1-1所示.观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
根据样本相关系数的定义,
图8.1-1
利用计算工具计算可得
代入①式,得????≈19?403.2?14×48.07×27.2634??181?14×48.072×11??051.77?14×27.262≈0.97.
由样本相关系数????≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
?
例2 有人收集了某城市居民年收入(即所有居民在一年内收入的总和)与A商品销售额的
10年数据,如表8.1-2所示.
第????年
1
2
3
4
5
6
7
8
9
10
居民年收入/亿元
32.2
31.1
32.9
35.8
37.1
38.0
39.0
43.0
44.6
46.0
A商品销售额/万元
25.0
30.0
34.0
37.0
39.0
41.0
42.0
44.0
48.0
51.0
1
2
3
4
5
6
7
8
9
10
居民年收入/亿元
32.2
31.1
32.9
35.8
37.1
38.0
39.0
43.0
44.6
46.0
A商品销售额/万元
25.0
30.0
34.0
37.0
39.0
41.0
42.0
44.0
48.0
51.0
表8.1-2
画出散点图,判断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
解:画出成对样本数据的散点图,如图8.1-6所示.从散点图看,A商品销售额与居民年收入的样本数据呈现出线性相关关系.
由样本数据计算得样本相关系数r≈0.95.由此可以推断,A商品销售额与居民年收入正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强.
图8.1-6
例3 在某校高一年级中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如表8.1-3所示.
编号
身高/cm
体重/kg
臂展/cm
?
编号
身高/cm
体重/kg
臂展/cm
1
2
3
4
5
6
7
8
9
10
11
12
13
173
179
175
179
182
173
180
170
169
177
177
178
174
55
71
52
62
82
63
55
81
54
54
59
67
56
169
170
172
177
174
166
174
169
166
176
170
174
170
14
15
16
17
18
19
20
21
22
23
24
25
?
166
176
176
175
169
184
169
182
171
177
173
173
?
66
61
49
60
48
86
58
54
58
61
58
51
?
161
166
165
173
162
189
164
170
164
173
165
169
?
体重与身高、臂展与身高分别具有怎样的相关性?
解:根据样本数据分别画出体重与身高、臂展与身高的散点图,分别如图8.1-7(1)和(2)所示,两个散点图都呈现出线性相关的特征.
图8.1-7
(1) (2)
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,都为正线性相关.其中,臂展与身高的相关程度更高.
随堂小测
【解】(方法一)根据实际生活的经验可知,人的身高和体重之间存在相关关系.
(方法二)观察表格中的数据可知,人的体重随着身高的增高而增长,因此人的身高和体重之间存在相关关系.
(方法三)以????轴表示身高,以????轴表示体重,得到相应的散点图如图所示.我们会发现,随着身高的增高,体重基本上呈增长的趋势.所以体重与身高之间存在相关关系,并且是正相关.
?
2.对四组数据进行统计,获得如图所示的散点图,关于其相关系数的比较,正确的是( )
A.????2 C.????4?
A
相关系数为????1 相关系数为????2?????????????????????????????????????相关系数为????3 相关系数为????4
(1) (2) (3) (4)
?
课堂小结
变量的相关关系
散点图
样本相关系数
正相关、负相关
线性相关、非线性相关
谢 谢!
