高中数学选择性必修第三册RJ·B--5.3 等比数列-5.3.1 等比数列 课件(共34页)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·B--5.3 等比数列-5.3.1 等比数列 课件(共34页) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 08:56:33 | ||
图片预览









文档简介
第五章
5.3
等比数列
5.3.1 等比数列
学习目标
1. 理解等比数列的定义,并能利用定义判断或证明一个数列是否为等比数列.
2.掌握等比数列的通项公式,并能运用解决简单问题.
3.了解等比中项的概念.
4.体会等比数列与指数函数的关系.
核心素养:数学运算、逻辑推理
新知学习
我们知道,等差数列的特征是“从第2项起,每一项与它的前一项之差都等于同一个常数”,类比等差数列的研究思路和方法,从运算的角度出发,你觉得还有怎样的数列是值得研究的?
复习引入
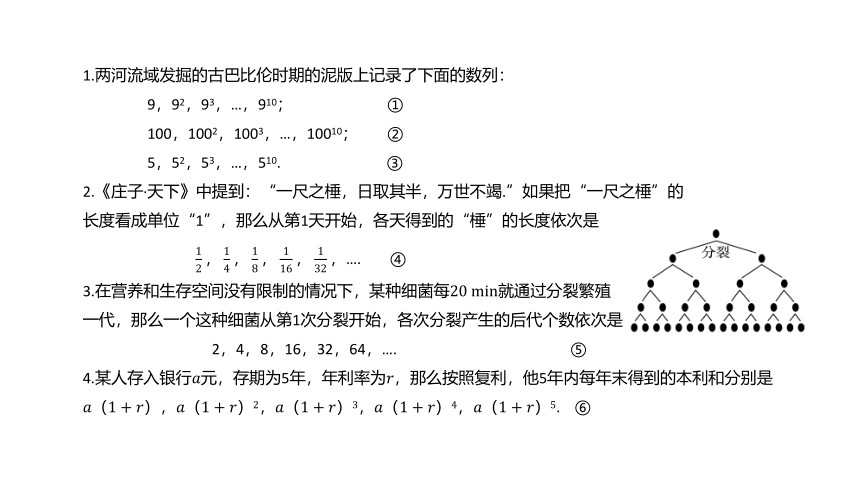
1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
????9,92,93,…,910; ①
????100,1002,1003,…,10010; ②
????5,52,53,…,510. ③
2.《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果把“一尺之棰”的
长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是
???????12,14,18,116,132,…. ④
3.在营养和生存空间没有限制的情况下,某种细菌每20?min就通过分裂繁殖
一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是
????????2,4,8,16,32,64,…. ⑤
4.某人存入银行????元,存期为5年,年利率为????,那么按照复利,他5年内每年末得到的本利和分别是
????(1+????),????(1+????)2,????(1+????)3,????(1+????)4,????(1+????)5. ⑥
?
探究:类比等差数列的研究,你认为可以通过怎样的运算发现以上数列的取值规律?
你发现了什么规律?
我们可以通过除法运算探究以上数列的取值规律.
如果用{????????}表示数列①,那么有
?
1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
????9,92,93,…,910; ①
????100,1002,1003,…,10010; ②
????5,52,53,…,510. ③
这表明,数列①有这样的取值规律:从第2项起,每一项与它的前一项之比都等于9.
其余几个数列也有这样的取值规律吗?请自己试一下.
一、等比数列的概念
一般地,如果数列{????????}从第2项起,每一项与它的前一项之比都等于同一个常数q,即
????????+1????????=q
恒成立,则称{an}为等比数列,其中q称为等比数列的公比.
例如,数列①~⑥的公比依次是 9,100,5,12,2,1+????.
?
新知讲解
对等比数列的概念理解
(1)“从第2项起”是因为首项没有“前一项”.
(2)对所有的正整数n,????????+1????????均为同一个常数,即比值相等,这就是等比数列公比的意义,同时还要注意公比是每一项与它的前一项的比值,防止前后次序颠倒.
(3)若一个数列不是从第2项起,而是从第3项或第4项起每一项与它的前一项的比都是同一个常数,则此数列不是等比数列,但是可以说此数列从第3项或第4项起是一个等比数列.
(4)常数列都是等差数列,但不一定是等比数列,只有当常数列各项不为0时,才是等比数列.
?
即时巩固
下列数列为等比数列的是( )
A.????,????2,????3?,????4,??
B.22,42,62,82, ?
C.?????1,?????12,?????13,?????14,?
D.1????,1????2, 1????3, 1????4, ?
?
D
二、等比数列的通项公式
探究:你能根据等比数列的定义推导它的通项公式吗?
一般地,如果等比数列{an}的首项是a1,公比是q,那么根据等比数列的定义可知????????+1????????=q,
即an+1=anq,从而 a2=a1q,
a3=a2q=(a1q)q=a1q2,
a4=a3q=(a1q2)q= a1q3,
……
由此可归纳出等比数列的通项公式为 an=a1qn-1.
另外,由等比数列的定义可得?????????????????1=q,?????????1?????????2=q,……????3????2=q,????2????1=q,
将这n-1个式子两边分别相乘,则有????????????1=qn-1,
?
因此同样可以得到等比数列的通项公式为????????=????1?????????1.
?
即时巩固
已知等比数列{an}的首项为a1=27,公比q=13.
(1)求a8 .
(2)判断18是否是这个数列中的项.如果是,求出是第几项;如果不是,说明理由.
?
解(1)由等比数列的通项公式可知a8=a1q7=27×137=181.
(2)设18是数列中的第n项,则27×13?????1=18,化简得32-n=2,
因为这个方程无正整数解,所以18不是数列中的项.
?
提示
等比数列通项公式的应用
①在已知首项a1和公比q的前提下,利用通项公式an=a1qn-1可求出等比数列中的任意一项.
②在公式an=a1qn-1中,有an,a1,q,n四个量,如果已知任意三个,可求出第四个量.
③可以利用通项公式来判断数列是否为等比数列.
④在记忆公式时,要注意q的指数比项数n小1这一特点.
三、等比数列与指数函数的关系
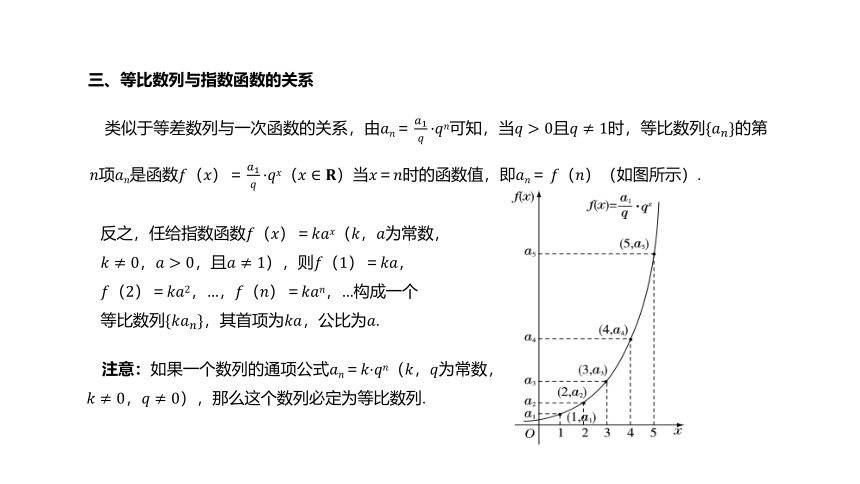
类似于等差数列与一次函数的关系,由????????=????1????·????????可知,当????>0且????≠1时,等比数列{????????}的第????项????????是函数????(????)=????1????·????????(????∈????)当????=????时的函数值,即????????=?????(????)(如图所示).
?
反之,任给指数函数????(????)=????????????(????,????为常数,
????≠0,????>0,且????≠1),则????(1)=????????,
????(2)=????????2,…,????(????)=????????????,…构成一个
等比数列{????????????},其首项为????????,公比为????.
?
注意:如果一个数列的通项公式????????=????·????????(????,????为常数,????≠0,????≠0),那么这个数列必定为等比数列.
?
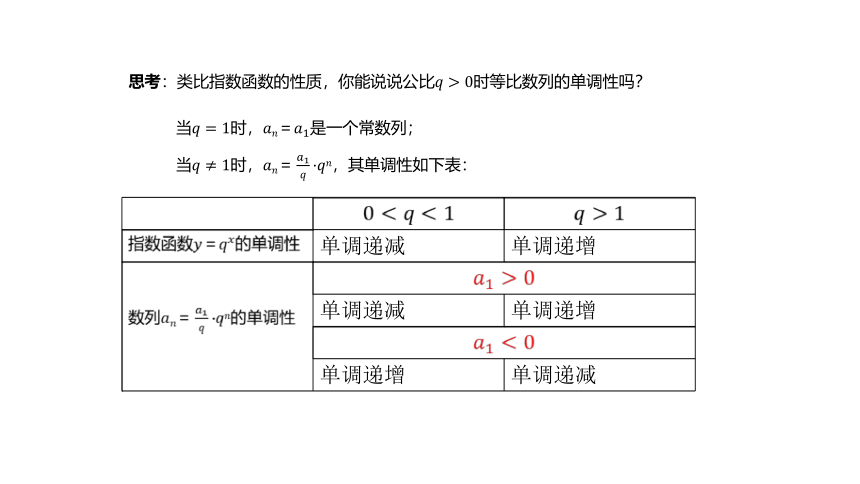
思考:类比指数函数的性质,你能说说公比????>0时等比数列的单调性吗?
?
当????=1时,????????=????1是一个常数列;
当????≠1时,????????=????1????·????????,其单调性如下表:
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0????>1
指数函数????=????????的单调性
单调递减
单调递增
数列????????=????1????·????????的单调性
????1>0
单调递减
单调递增
????1<0
单调递增
单调递减
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单调递减
单调递增
单调递减
单调递增
单调递增
单调递减
二、等比中项
如果????,????,????成等比数列,那么????叫做????与????的等比中项.
根据等比中项与等比数列的张定义可知????????=????????,因此G 2=xy.由此可知G=±????????.
?
等比中项的理解
1.显然,两个正数(或两个负数)的等比中项有两个,它们互为相反数,如2+1,2 -1的等比中项为±1.一个正数和一个负数没有等比中项.
2.一个等比数列中,从第2项起,每一项(有穷等比数列的末项除外)都是它的前一项与后一项的等比中项;反之,如果一个数列从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等比中项,即????????2=an-1an+1(n≥2),那么这个数列是等比数列.等比中项法是证明一个数列为等比数列的方法之一.
3.任意两个实数未必一定有等比中项,如0和任何实数都无等比中项.
?
即时巩固
在4与14之间插入3个数,使这5个数成等比数列,求插入的3个数.
?
解(方法一)依题意,a1=4,a5=14,由等比数列的通项公式,得14=4×q4,解得 q=±12.
当q=12时,插入的3个数分别为4×12=2,2×12=1,1×12=12;
当q=-12时,插入的3个数分别为4×?12=-2,(-2)×?12=1,1×?12=-12.
因此,插入的3个数分别为2,1,12或-2,1,-12.
?
(方法二)因为等比数列共有5项,即a1, a2, a3, a4, a5 .
又因为2×3=1+5,所以????32=a1a5=4×14=1,即a3=±1.
又因为a3要与a1同号,因此a3=1.
类似地,有????22=a1a3,????42=a3a张韵5,而且a2与a4同号.因此
当a2=????1????3=4×1=2时,a4=????3????5=1×14=12;
当a2=-????1????3=-4×1=-2时,a4=-????3????5=-1×14=-12.
因此,插入的3个数分别为2,1,12或-2,1,-12.
?
知识拓展:等比数列的性质
(1)若数列{????????},{????????}都是等比数列,则{????????????????},{????????????????},{????????????}(????≠0),1????????,{????????2}等也是等比数列.
?
(2)①将等比数列的前????项去掉,剩余各项组成的新数列仍为等比数列;
②从等比数列中每隔相同的项取出一项,所得的新数列仍为等比数列
(新数列的下标成等差数列)
?
(3)已知数列{????????}是等比数列,????,????,????,????∈?????,
若????+????=?????+????,则有?????????????????=????????????????.
特别地,若????+????=2????,则有?????????????????=????????2
?
即时巩固
已知数列{????????}的首项????1=3.
(1)若{????????}为等差数列,公差????=2,证明数列{3????????}为等比数列;
(2)若{????????}为等比数列,公比????=19,证明数列{log?3????????}为等差数列.
?
证明:(1)由????1=3,????=2,得{????????}的通项公式为????????=2????+1.
设????????=3????????,则
?
又?????1=33=27,所以,{3????????}是以27为首项,9为公比的等比数列.
(2)由????1=3,????=19,得????????=3×19?????1=33?2????.
两边取以3为底的对数,得log3????????=log333?2????=3?2????.
所以log3????????+1?log3????????=[3?2(????+1)]?(3?2????)=?2.
又log3????1=log33=1,
所以,{log3????????}是首项为1,公差为?2的等差数列.
?
典例剖析
例1 若等比数列{????????}的第4项和第6项分别为48和12,求{????????}的第5项.
分析:等比数列{????????}由????1,????唯一确定,可利用条件列出关于????1,????的方程(组),进行求解.
?
解法1:由????4=48,????6=12,得
?
②的两边分别除以①的两边,得????2=14, 解得????=12或?12.
把????=12代入①,得????1=384.????此时????5=????1????4=384×124=24.
把????=?12代入①,得????1=?384.
此时????5=????1????4=?384×?124=?24.
因此,{????????}的第5项是24或?24.
?
解法2:因为????5是????4与????6的等比中项,所以
????52=????4????6=48×12=576.
所以????5=±576=±24.
因此,{????????}的第5项是24或?24.
?
类题通法
等比数列求基本量的常用方法
(1)用通项公式列方程或方程组求解a1及q,然后求其他的量;
(2)充分利用各项之间的关系,求出q后,利用公式的变形an=am?????????????求解.
?
例2 一个等比数列的前三项依次是a,2a+2,3a+3,那么-1312是该数列中的第 项.
?
解析 ∵ a,2a+2,3a+3是等比数列的前三项,
∴ a(3a+3)=(2a+2)2,解得a=-1或a=-4.
当a=-1时,数列的前三项依次为-1,0,0,与等比数列的定义矛盾,故将a=-1舍去.
当a=-4时,数列的前三项依次为-4,-6,-9,则公比q=32.
∴ an=-4·32?????1.
令-4·32?????1=-1312,即32?????1=278=323.
∴ n-1=3,即n=4.
∴ -1312是该数列的第4项.
答案 4
?
点评
(1)由定义可知ab≠0,G 2=ab,即G=±????????.
(2)只有同号的两个数才有等比中项,等比中项有两个,它们互为相反数.
(3)三个数a,G,b成等比数列的一个必要不充分条件是G 2=ab.
?
例3 已知a,b,c,d成等比数列,a+b,b+c,c+d均不为零,求证:a+b,b+c,c+d成等比数列.
证明 (方法1)由已知,设????????=????????=????????=q(q为常数且q≠0).
∵ a+b,b+c,c+d均不为零,∴????+????????+????=????+????????+????=q,
故a+b,b+c,c+d成等比数列.
(方法2)由已知得b2=ac,c2=bd,????????=????????,即bc=ad,
∴ (b+c)2=b2+c2+2bc=ac+bd+bc+bc=ac+bd+bc+ad=(ac+bc)+(bd+ad)=(a+b)· (c+d),且a+b,b+c,c+d均不为零,∴ a+b,b+c,c+d成等比数列.
(方法3)由已知,设b=aq,c=aq2,d=aq3(q为常数且q≠0).
∵ a+b,b+c,c+d均不为零,
∴????+????????+????=????????1+????????1+????=q,????+????????+????=????????21+????????????1+????=q,故a+b,b+c,c+d成等比数列.
?
类题通法
等比数列的判定方法
1.定义法:????????+1????????=q(q为常数且q≠0)或?????????????????1=q(q为常数且q≠0,n≥2)?{an}为等比数列.
2.等比中项法:????????+12=an·an+2(an≠0)?{an}为等比数列.
3.通项公式法:an=a1qn-1(a1,q为非零常数)?{an}为等比数列.
定义法和等比中项法是最常用的判定方法.
注意不能仅由数列的前有限项成等比数列得出数列是等比数列,而要否定一个数列是等比数列,只需得到其任意连续三项不成等比数列即可.
?
例4 数列{????????}共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132.求这个数列.
分析:先利用已知条件表示出数列的各项,再进一步根据条件列方程组求解.
?
解:设前三项的公比为????,后三项的公差为????,则数列的各项依次为80????2,80????,80,80+????,80+2????.于是得
?
解方程组,得
所以这个数列是20,40,80,96,112,或180,120,80,16,?48.
?
类题通法
几个数成等比数列的设法
1.三个数成等比数列设为????????,a,aq.
2.四个符号相同的数成等比数列设为????????3,????????,aq,aq3.
?
例5 已知数列{an}中,a1=56,an+1=13an+12????+1,求通项公式an.
?
解:令an+1-A×12????+1=13?????????????×12????,则an+1=13an+????3×12????+1.
由已知条件知????3=1,得A=3,
所以an+1-3×12????+1=13?????????3×12????.
又a1-3×121=-23≠0,
所以?????????3×12????是首项为-23,公比为13的等比数列.
所以an-3×12????=-23×13?????1,故an=3×12????-2×13????.
?
类题通法
构造等比数列的常用技巧
1.常用来求形如“an+1=pan+q(p≠1)”的数列的通项公式,可以证明????????+?????????1为等比数列.
2.形如an+1=can+dn(c≠d,cd≠0)的递推关系式,除利用待定系数法直接化归为等比数列外,也可以两边同除以dn+1得????????+1????????+1=????????×????????????????+1????,进而化归为等比数列;还可以两边同除以cn+1得????????+1????????+1=????????????????+????????????×1????,再利用累加法求出????????????????,即得an.
?
例6 容积为a L(a>1)的容器盛满酒精后倒出1 L,然后加满水,混合溶液后再倒出 1 L,又用水加满,如此继续下去,问第n次操作后溶液的浓度是多少?若a=2,则至少应倒出几次后才可以使酒精浓度低于10%?
解 开始的浓度为1,操作一次后溶液的浓度是a1=1-1????.
设操作n次后溶液的浓度是an,则操作n+1次后溶液的浓度是an+1=????????1?1????.
所以{an}构成以a1=1-1????为首项,q=1-1????为公比的等比数列.
所以an=a1qn-1=1?1????????,
即第n次操作后溶液的浓度是1?1????????.
当a=2时,由an=12????<110,得n≥4.
因此,若a=2,则至少应倒出4次后才可以使酒精浓度低于10%.
?
点评
将实际问题通过建模转化为数列问题时应注意
(1)确定是等差数列还是等比数列;
(2)确定是求an还是求Sn,特别是要准确确定项数n;
(3)确定递推关系.
随堂小测
1.在等比数列{????????}中,????2+????4=1,????6+????8=9,则????2=(??)
A.14 B.13 C.12 D.4
?
A
2.等比数列{????????}的公比为2,则 的值为( )
A.1 B.12 C.14 D.18
?
C
4.已知正项等比数列{????????}的公比为3,若????????????????=9????22,则2????+12????的最小值等于( )
A.1 B.12 C.34 D.32
?
C
5.若等差数列{????????}和等比数列{????????}满足????1=????1=?1,????4=????4=8,则????2????2= .
?
1
3.公差不为零的等差数列的第二、三、六项依次成等比数列,则公比是(??)
A.2 B.3 C.4 D.5
B
6.已知{an}是等差数列,满足a1=2,a4=14,数列{bn}满足b1=1,b4=6,且{an-bn} 是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)若对任意n∈N+,都有bn≤bk成立,求正整数k的值.
解(1)设{an}的公差为d,则d=????4?????13=4,所以an=2+(n-1)×4=4n-2.
故{an}的通项公式为an=4n-2(n∈N+).
设cn=an-bn,则c1=a1-b1=2-1=1,c4=a4-b4=14-6=8.
因为{cn}为等比数列,所以设{cn}的公比为q,则q3=????4????1=8,解得q=2,
所以cn=2n-1,即an-bn=2n-1,所以bn=4n-2-2n-1(n∈N+).
(2)由题意,得bk应为数列{bn}的最大项.
由(1)得bn+1-bn=4(n+1)-2-2n-4n+2+2n-1=4-2n-1(n∈N+),
当n<3时,bn+1-bn>0,bn当n=3时,bn+1-bn=0,即b3=b4;
当n>3时,bn+1-bn<0,bn>bn+1,即b4>b5>b6>….
综上所述, 数列{bn}中的最大项为b3和b4.故正整数k的值为3或4.
?
课堂小结
知识清单:
等比数列的定义;等比数列的通项公式;等比数列与指数函数的关系;等比中项;等比数列的性质.
方法归纳:方程思想
常见误区:忽略等比数列的项均不为零;忽略等比数列的项的符号.
谢 谢!
5.3
等比数列
5.3.1 等比数列
学习目标
1. 理解等比数列的定义,并能利用定义判断或证明一个数列是否为等比数列.
2.掌握等比数列的通项公式,并能运用解决简单问题.
3.了解等比中项的概念.
4.体会等比数列与指数函数的关系.
核心素养:数学运算、逻辑推理
新知学习
我们知道,等差数列的特征是“从第2项起,每一项与它的前一项之差都等于同一个常数”,类比等差数列的研究思路和方法,从运算的角度出发,你觉得还有怎样的数列是值得研究的?
复习引入
1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
????9,92,93,…,910; ①
????100,1002,1003,…,10010; ②
????5,52,53,…,510. ③
2.《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果把“一尺之棰”的
长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是
???????12,14,18,116,132,…. ④
3.在营养和生存空间没有限制的情况下,某种细菌每20?min就通过分裂繁殖
一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是
????????2,4,8,16,32,64,…. ⑤
4.某人存入银行????元,存期为5年,年利率为????,那么按照复利,他5年内每年末得到的本利和分别是
????(1+????),????(1+????)2,????(1+????)3,????(1+????)4,????(1+????)5. ⑥
?
探究:类比等差数列的研究,你认为可以通过怎样的运算发现以上数列的取值规律?
你发现了什么规律?
我们可以通过除法运算探究以上数列的取值规律.
如果用{????????}表示数列①,那么有
?
1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
????9,92,93,…,910; ①
????100,1002,1003,…,10010; ②
????5,52,53,…,510. ③
这表明,数列①有这样的取值规律:从第2项起,每一项与它的前一项之比都等于9.
其余几个数列也有这样的取值规律吗?请自己试一下.
一、等比数列的概念
一般地,如果数列{????????}从第2项起,每一项与它的前一项之比都等于同一个常数q,即
????????+1????????=q
恒成立,则称{an}为等比数列,其中q称为等比数列的公比.
例如,数列①~⑥的公比依次是 9,100,5,12,2,1+????.
?
新知讲解
对等比数列的概念理解
(1)“从第2项起”是因为首项没有“前一项”.
(2)对所有的正整数n,????????+1????????均为同一个常数,即比值相等,这就是等比数列公比的意义,同时还要注意公比是每一项与它的前一项的比值,防止前后次序颠倒.
(3)若一个数列不是从第2项起,而是从第3项或第4项起每一项与它的前一项的比都是同一个常数,则此数列不是等比数列,但是可以说此数列从第3项或第4项起是一个等比数列.
(4)常数列都是等差数列,但不一定是等比数列,只有当常数列各项不为0时,才是等比数列.
?
即时巩固
下列数列为等比数列的是( )
A.????,????2,????3?,????4,??
B.22,42,62,82, ?
C.?????1,?????12,?????13,?????14,?
D.1????,1????2, 1????3, 1????4, ?
?
D
二、等比数列的通项公式
探究:你能根据等比数列的定义推导它的通项公式吗?
一般地,如果等比数列{an}的首项是a1,公比是q,那么根据等比数列的定义可知????????+1????????=q,
即an+1=anq,从而 a2=a1q,
a3=a2q=(a1q)q=a1q2,
a4=a3q=(a1q2)q= a1q3,
……
由此可归纳出等比数列的通项公式为 an=a1qn-1.
另外,由等比数列的定义可得?????????????????1=q,?????????1?????????2=q,……????3????2=q,????2????1=q,
将这n-1个式子两边分别相乘,则有????????????1=qn-1,
?
因此同样可以得到等比数列的通项公式为????????=????1?????????1.
?
即时巩固
已知等比数列{an}的首项为a1=27,公比q=13.
(1)求a8 .
(2)判断18是否是这个数列中的项.如果是,求出是第几项;如果不是,说明理由.
?
解(1)由等比数列的通项公式可知a8=a1q7=27×137=181.
(2)设18是数列中的第n项,则27×13?????1=18,化简得32-n=2,
因为这个方程无正整数解,所以18不是数列中的项.
?
提示
等比数列通项公式的应用
①在已知首项a1和公比q的前提下,利用通项公式an=a1qn-1可求出等比数列中的任意一项.
②在公式an=a1qn-1中,有an,a1,q,n四个量,如果已知任意三个,可求出第四个量.
③可以利用通项公式来判断数列是否为等比数列.
④在记忆公式时,要注意q的指数比项数n小1这一特点.
三、等比数列与指数函数的关系
类似于等差数列与一次函数的关系,由????????=????1????·????????可知,当????>0且????≠1时,等比数列{????????}的第????项????????是函数????(????)=????1????·????????(????∈????)当????=????时的函数值,即????????=?????(????)(如图所示).
?
反之,任给指数函数????(????)=????????????(????,????为常数,
????≠0,????>0,且????≠1),则????(1)=????????,
????(2)=????????2,…,????(????)=????????????,…构成一个
等比数列{????????????},其首项为????????,公比为????.
?
注意:如果一个数列的通项公式????????=????·????????(????,????为常数,????≠0,????≠0),那么这个数列必定为等比数列.
?
思考:类比指数函数的性质,你能说说公比????>0时等比数列的单调性吗?
?
当????=1时,????????=????1是一个常数列;
当????≠1时,????????=????1????·????????,其单调性如下表:
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0????>1
指数函数????=????????的单调性
单调递减
单调递增
数列????????=????1????·????????的单调性
????1>0
单调递减
单调递增
????1<0
单调递增
单调递减
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单调递减
单调递增
单调递减
单调递增
单调递增
单调递减
二、等比中项
如果????,????,????成等比数列,那么????叫做????与????的等比中项.
根据等比中项与等比数列的张定义可知????????=????????,因此G 2=xy.由此可知G=±????????.
?
等比中项的理解
1.显然,两个正数(或两个负数)的等比中项有两个,它们互为相反数,如2+1,2 -1的等比中项为±1.一个正数和一个负数没有等比中项.
2.一个等比数列中,从第2项起,每一项(有穷等比数列的末项除外)都是它的前一项与后一项的等比中项;反之,如果一个数列从第2项起,每一项(有穷数列的末项除外)都是它的前一项与后一项的等比中项,即????????2=an-1an+1(n≥2),那么这个数列是等比数列.等比中项法是证明一个数列为等比数列的方法之一.
3.任意两个实数未必一定有等比中项,如0和任何实数都无等比中项.
?
即时巩固
在4与14之间插入3个数,使这5个数成等比数列,求插入的3个数.
?
解(方法一)依题意,a1=4,a5=14,由等比数列的通项公式,得14=4×q4,解得 q=±12.
当q=12时,插入的3个数分别为4×12=2,2×12=1,1×12=12;
当q=-12时,插入的3个数分别为4×?12=-2,(-2)×?12=1,1×?12=-12.
因此,插入的3个数分别为2,1,12或-2,1,-12.
?
(方法二)因为等比数列共有5项,即a1, a2, a3, a4, a5 .
又因为2×3=1+5,所以????32=a1a5=4×14=1,即a3=±1.
又因为a3要与a1同号,因此a3=1.
类似地,有????22=a1a3,????42=a3a张韵5,而且a2与a4同号.因此
当a2=????1????3=4×1=2时,a4=????3????5=1×14=12;
当a2=-????1????3=-4×1=-2时,a4=-????3????5=-1×14=-12.
因此,插入的3个数分别为2,1,12或-2,1,-12.
?
知识拓展:等比数列的性质
(1)若数列{????????},{????????}都是等比数列,则{????????????????},{????????????????},{????????????}(????≠0),1????????,{????????2}等也是等比数列.
?
(2)①将等比数列的前????项去掉,剩余各项组成的新数列仍为等比数列;
②从等比数列中每隔相同的项取出一项,所得的新数列仍为等比数列
(新数列的下标成等差数列)
?
(3)已知数列{????????}是等比数列,????,????,????,????∈?????,
若????+????=?????+????,则有?????????????????=????????????????.
特别地,若????+????=2????,则有?????????????????=????????2
?
即时巩固
已知数列{????????}的首项????1=3.
(1)若{????????}为等差数列,公差????=2,证明数列{3????????}为等比数列;
(2)若{????????}为等比数列,公比????=19,证明数列{log?3????????}为等差数列.
?
证明:(1)由????1=3,????=2,得{????????}的通项公式为????????=2????+1.
设????????=3????????,则
?
又?????1=33=27,所以,{3????????}是以27为首项,9为公比的等比数列.
(2)由????1=3,????=19,得????????=3×19?????1=33?2????.
两边取以3为底的对数,得log3????????=log333?2????=3?2????.
所以log3????????+1?log3????????=[3?2(????+1)]?(3?2????)=?2.
又log3????1=log33=1,
所以,{log3????????}是首项为1,公差为?2的等差数列.
?
典例剖析
例1 若等比数列{????????}的第4项和第6项分别为48和12,求{????????}的第5项.
分析:等比数列{????????}由????1,????唯一确定,可利用条件列出关于????1,????的方程(组),进行求解.
?
解法1:由????4=48,????6=12,得
?
②的两边分别除以①的两边,得????2=14, 解得????=12或?12.
把????=12代入①,得????1=384.????此时????5=????1????4=384×124=24.
把????=?12代入①,得????1=?384.
此时????5=????1????4=?384×?124=?24.
因此,{????????}的第5项是24或?24.
?
解法2:因为????5是????4与????6的等比中项,所以
????52=????4????6=48×12=576.
所以????5=±576=±24.
因此,{????????}的第5项是24或?24.
?
类题通法
等比数列求基本量的常用方法
(1)用通项公式列方程或方程组求解a1及q,然后求其他的量;
(2)充分利用各项之间的关系,求出q后,利用公式的变形an=am?????????????求解.
?
例2 一个等比数列的前三项依次是a,2a+2,3a+3,那么-1312是该数列中的第 项.
?
解析 ∵ a,2a+2,3a+3是等比数列的前三项,
∴ a(3a+3)=(2a+2)2,解得a=-1或a=-4.
当a=-1时,数列的前三项依次为-1,0,0,与等比数列的定义矛盾,故将a=-1舍去.
当a=-4时,数列的前三项依次为-4,-6,-9,则公比q=32.
∴ an=-4·32?????1.
令-4·32?????1=-1312,即32?????1=278=323.
∴ n-1=3,即n=4.
∴ -1312是该数列的第4项.
答案 4
?
点评
(1)由定义可知ab≠0,G 2=ab,即G=±????????.
(2)只有同号的两个数才有等比中项,等比中项有两个,它们互为相反数.
(3)三个数a,G,b成等比数列的一个必要不充分条件是G 2=ab.
?
例3 已知a,b,c,d成等比数列,a+b,b+c,c+d均不为零,求证:a+b,b+c,c+d成等比数列.
证明 (方法1)由已知,设????????=????????=????????=q(q为常数且q≠0).
∵ a+b,b+c,c+d均不为零,∴????+????????+????=????+????????+????=q,
故a+b,b+c,c+d成等比数列.
(方法2)由已知得b2=ac,c2=bd,????????=????????,即bc=ad,
∴ (b+c)2=b2+c2+2bc=ac+bd+bc+bc=ac+bd+bc+ad=(ac+bc)+(bd+ad)=(a+b)· (c+d),且a+b,b+c,c+d均不为零,∴ a+b,b+c,c+d成等比数列.
(方法3)由已知,设b=aq,c=aq2,d=aq3(q为常数且q≠0).
∵ a+b,b+c,c+d均不为零,
∴????+????????+????=????????1+????????1+????=q,????+????????+????=????????21+????????????1+????=q,故a+b,b+c,c+d成等比数列.
?
类题通法
等比数列的判定方法
1.定义法:????????+1????????=q(q为常数且q≠0)或?????????????????1=q(q为常数且q≠0,n≥2)?{an}为等比数列.
2.等比中项法:????????+12=an·an+2(an≠0)?{an}为等比数列.
3.通项公式法:an=a1qn-1(a1,q为非零常数)?{an}为等比数列.
定义法和等比中项法是最常用的判定方法.
注意不能仅由数列的前有限项成等比数列得出数列是等比数列,而要否定一个数列是等比数列,只需得到其任意连续三项不成等比数列即可.
?
例4 数列{????????}共有5项,前三项成等比数列,后三项成等差数列,第3项等于80,第2项与第4项的和等于136,第1项与第5项的和等于132.求这个数列.
分析:先利用已知条件表示出数列的各项,再进一步根据条件列方程组求解.
?
解:设前三项的公比为????,后三项的公差为????,则数列的各项依次为80????2,80????,80,80+????,80+2????.于是得
?
解方程组,得
所以这个数列是20,40,80,96,112,或180,120,80,16,?48.
?
类题通法
几个数成等比数列的设法
1.三个数成等比数列设为????????,a,aq.
2.四个符号相同的数成等比数列设为????????3,????????,aq,aq3.
?
例5 已知数列{an}中,a1=56,an+1=13an+12????+1,求通项公式an.
?
解:令an+1-A×12????+1=13?????????????×12????,则an+1=13an+????3×12????+1.
由已知条件知????3=1,得A=3,
所以an+1-3×12????+1=13?????????3×12????.
又a1-3×121=-23≠0,
所以?????????3×12????是首项为-23,公比为13的等比数列.
所以an-3×12????=-23×13?????1,故an=3×12????-2×13????.
?
类题通法
构造等比数列的常用技巧
1.常用来求形如“an+1=pan+q(p≠1)”的数列的通项公式,可以证明????????+?????????1为等比数列.
2.形如an+1=can+dn(c≠d,cd≠0)的递推关系式,除利用待定系数法直接化归为等比数列外,也可以两边同除以dn+1得????????+1????????+1=????????×????????????????+1????,进而化归为等比数列;还可以两边同除以cn+1得????????+1????????+1=????????????????+????????????×1????,再利用累加法求出????????????????,即得an.
?
例6 容积为a L(a>1)的容器盛满酒精后倒出1 L,然后加满水,混合溶液后再倒出 1 L,又用水加满,如此继续下去,问第n次操作后溶液的浓度是多少?若a=2,则至少应倒出几次后才可以使酒精浓度低于10%?
解 开始的浓度为1,操作一次后溶液的浓度是a1=1-1????.
设操作n次后溶液的浓度是an,则操作n+1次后溶液的浓度是an+1=????????1?1????.
所以{an}构成以a1=1-1????为首项,q=1-1????为公比的等比数列.
所以an=a1qn-1=1?1????????,
即第n次操作后溶液的浓度是1?1????????.
当a=2时,由an=12????<110,得n≥4.
因此,若a=2,则至少应倒出4次后才可以使酒精浓度低于10%.
?
点评
将实际问题通过建模转化为数列问题时应注意
(1)确定是等差数列还是等比数列;
(2)确定是求an还是求Sn,特别是要准确确定项数n;
(3)确定递推关系.
随堂小测
1.在等比数列{????????}中,????2+????4=1,????6+????8=9,则????2=(??)
A.14 B.13 C.12 D.4
?
A
2.等比数列{????????}的公比为2,则 的值为( )
A.1 B.12 C.14 D.18
?
C
4.已知正项等比数列{????????}的公比为3,若????????????????=9????22,则2????+12????的最小值等于( )
A.1 B.12 C.34 D.32
?
C
5.若等差数列{????????}和等比数列{????????}满足????1=????1=?1,????4=????4=8,则????2????2= .
?
1
3.公差不为零的等差数列的第二、三、六项依次成等比数列,则公比是(??)
A.2 B.3 C.4 D.5
B
6.已知{an}是等差数列,满足a1=2,a4=14,数列{bn}满足b1=1,b4=6,且{an-bn} 是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)若对任意n∈N+,都有bn≤bk成立,求正整数k的值.
解(1)设{an}的公差为d,则d=????4?????13=4,所以an=2+(n-1)×4=4n-2.
故{an}的通项公式为an=4n-2(n∈N+).
设cn=an-bn,则c1=a1-b1=2-1=1,c4=a4-b4=14-6=8.
因为{cn}为等比数列,所以设{cn}的公比为q,则q3=????4????1=8,解得q=2,
所以cn=2n-1,即an-bn=2n-1,所以bn=4n-2-2n-1(n∈N+).
(2)由题意,得bk应为数列{bn}的最大项.
由(1)得bn+1-bn=4(n+1)-2-2n-4n+2+2n-1=4-2n-1(n∈N+),
当n<3时,bn+1-bn>0,bn
当n>3时,bn+1-bn<0,bn>bn+1,即b4>b5>b6>….
综上所述, 数列{bn}中的最大项为b3和b4.故正整数k的值为3或4.
?
课堂小结
知识清单:
等比数列的定义;等比数列的通项公式;等比数列与指数函数的关系;等比中项;等比数列的性质.
方法归纳:方程思想
常见误区:忽略等比数列的项均不为零;忽略等比数列的项的符号.
谢 谢!
