高中数学选择性必修第三册RJ·B--6.1 导数-6.1.1 函数的平均变化率 课件(共18张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·B--6.1 导数-6.1.1 函数的平均变化率 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览






文档简介
第六章
6.1
导数
6.1.1 函数的平均变化率
学习目标
核心素养:数学抽象、直观想象、数学运算
1.理解函数平均变化率的概念,会用对应的符号语言刻画函数的平均变化率;了解函数平均变化率的几何意义.
2.会求函数的平均变化率;理解函数平均变化率的模型.
3.理解符号“????????????????”的含义.
?
新知学习
情境与问题
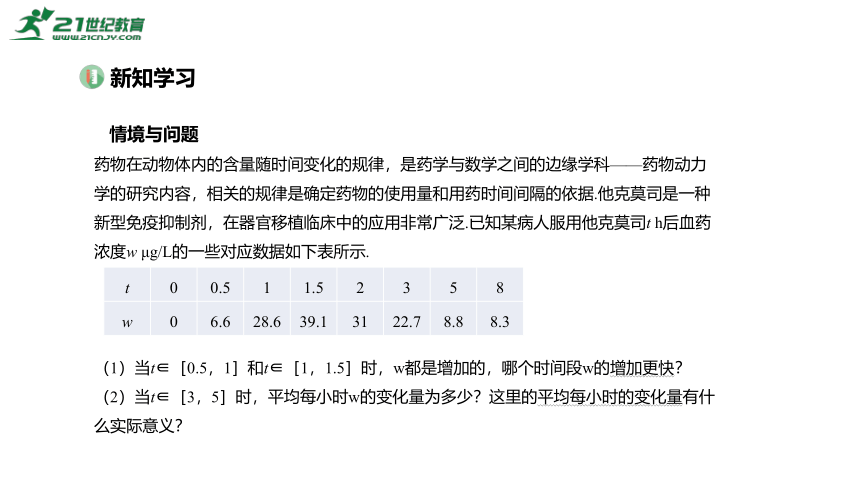
药物在动物体内的含量随时间变化的规律,是药学与数学之间的边缘学科——药物动力学的研究内容,相关的规律是确定药物的使用量和用药时间间隔的依据.他克莫司是一种新型免疫抑制剂,在器官移植临床中的应用非常广泛.已知某病人服用他克莫司t h后血药浓度w μg/L的一些对应数据如下表所示.
(1)当t∈[0.5,1]和t∈[1,1.5]时,w都是增加的,哪个时间段w的增加更快?
(2)当t∈[3,5]时,平均每小时w的变化量为多少?这里的平均每小时的变化量有什么实际意义?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t
0
0.5
1
1.5
2
3
5
8
w
0
6.6
28.6
39.1
31
22.7
8.8
8.3
提示解读
由所给数据不难看出,当t∈[0.5,1]和t∈[1,1.5]时,w的增加量分别为
28.6-6.6=22,39.1-28.6=10.5,
因为时间间隔都是0.5 h,所以t∈[0.5,1]时,w增加更快.
当t∈[3,5]时,w的变化量为
8.8-22.7=-13.9 ,
又因为共有5-3=2(h),所以平均每小时的变化量为?13.92=-6.95.这说明,在[3,5]这段时间内,任意1个小时血药浓度平均减少6.95 μg/L,此时,任意h(h∈[0,2])个小时血药浓度平均减少6.95 h μg/L.
?
总结归纳:函数的平均变化率
1.定义
一般地,若函数y=f(x)的定义域为D,且
x1,x2∈D,x1≠x2,y1=f(x1),y2=f(x2),
则称Δx=x2-x1为自变量的改变量;
称Δy=y2-y1(或Δf=f(x2)-f(x1))为相应的因变量的改变量;
称????????????????=????2?????1????2?????1或????????????????=????????2?????????1????2?????1 为函数y=f(x)在以x1,x2为端点的闭区间上的平均变化率,
其中“以x1,x2为端点的闭区间”,在x1x2时指的是[x2,x1].
2.意义
平均变化率的实际意义是,在以x1,x2为端点的闭区间上,自变量每增加1个单位,因变量平均将增加????????????????个单位.因此,如果自变量增加h个单位,那么因变量将增加????????????????h个单位.
?
注意与提醒
(1)上述Δx在x1x2时是小于0的,而且x2总可以用x1和Δx表示,即x2=x1+Δx,此时“以x1,x2为端点的闭区间”也可表述为“以x1,x1+Δx为端点的闭区间”,而且
f(x2)=f(x1+Δx),因此平均变化率
????????????????=????????1+?????????????????1????1+?????????????1=????????1+?????????????????1????????.
(2)函数在x=x0处有定义.
(3)x1是x0附近的任意一点,所以Δx=x1-x0≠0,但Δx可为正值,也可为负值.
(4)改变量的对应:若Δx=x1-x0,则Δf=f(x1)-f(x0),而不是Δf=f(x0)-f(x1).
?
3.图形表示
函数在一个区间内的平均变化率,等于这个区间端点对应的函数图像上两点连线的斜率.例如,图中函数y=f(x)在[x1,x2]上的平均变化率,等于直线AB的斜率,其中
A(x1,f(x1)),B(x2,f(x2)).
因此,平均变化率近似地刻画了函数对应的曲线(即函数图像)在某一区间上的变化趋势,是曲线倾斜程度的“数量化”,曲线的倾斜程度是平均变化率的“直观化”.
注意
(1)函数在x0到x0+Δx的平均变化率的几何意义是曲线y=f(x)过点(x0,f(x0)),(x0+Δx,f(x0+Δx))的割线的斜率,平均变化率刻画了函数f(x)的图像在x0附近的
陡峭程度,其绝对值越大,图像越陡,反之越平缓.
(2)平均变化率是曲线陡峭程度的“数量化”,曲线陡峭程度是平均变化率的“直观化”.利用平均变化率可以刻画变量平均变化的趋势和快慢程度,但效果是“粗糙不精确的”.
只有当Δx无限变小时,这种量化才由“粗糙”逼近“精确”.
求函数f(x)=x2在下列区间上的平均变化率.
(1)[1,3];
(2)以1和1+Δx为端点的闭区间.
即时巩固
解 (1)依定义可知
????????????????=????3?????13?1=32?122=4,
即f(x)在[1,3]上的平均变化率为4.
(2)依定义可知
????????????????=????1+?????????????1????????=1+????????2?12????????=2+Δx,
f(x)在以1和1+Δx为端点的闭区间上的平均变化率为 2+Δx .
?
4.以直代曲
将图中的线段AB近似地看成w在[3,5]上的图像.
用直线段代替了曲线段,这在数学中简称为“以直代曲”.
5.平均速度与平均变化率
从物理学中我们知道,平均速度可以刻画物体在一段时间内运动的快慢.如果物体运动的位移
x m与时间t s的关系为x=h(t),则物体在[t1,t2](t1?????2??????1????2?????1(m/s).
这就是说,物体在某段时间内的平均速度等于x=h(t)在该段时间内的平均变化率.
?
已知某物体运动的位移x m是时间t s的函数,而且t=0.1时,x=0.25;t=0.5时,x=2.25.
(1)求这个物体在时间段[0.1,0.5]内的平均速度;
(2)估计出t=0.2时物体的位移.
解 (1)所求平均速度为2.25?0.250.5?0.1=20.4=5(m/s).
(2)将x在[0.1,0.5]上的图像看成直线,则由(1)可知,直线的斜率为5,
且直线通过点(0.1,0.25),因此,x与t的关系可近似地表示为x-0.25=5(t-0.1).
在上式中令t=0.2,可求得x=0.75,即t=0.2时物体的位移可以估计为0.75 m.
?
即时巩固
典例剖析
例1 已知函数f(x)=2x2+3x-5.
(1)求当x1=4,且Δx=1时,函数增量Δf和平均变化率????????????????;
(2)求当x1=4,且Δx=0.1时,函数增量Δf和平均变化率????????????????;
(3)若设x2=x1+Δx,分析(1)(2)中的平均变化率的几何意义.
?
解:∵ f(x)=2x2+3x-5,
∴ Δf=f(x1+Δx)-f(x1)=2(x1+Δx)2+3(x1+Δx)-5-(2????12+3x1-5)
=2[(Δx)2+2x1Δx]+3Δx=2(Δx)2+(4x1+3)Δx.
(1)当x1=4,且Δx=1时,Δf=2+(4×4+3)=21,????????????????=211=21.
(2)当x1=4,且Δx=0.1时,Δf=2×0.12+(4×4+3)×0.1=0.02+1.9=1.92.
????????????????=1.920.1=19.2.
(3)在(1)中,????????????????=????????2?????????1????2?????1=????5?????45?4,它表示过抛物线上的点(4,39)
与点(5,60)的直线的斜率.
在(2)中,????????????????=????????2?????????1????2?????1=????4.1?????44.1?4,它表示过抛物线上的点(4,39)与
点(4.1,40.92)的直线的斜率.
点评:求函数的平均变化率时要准确计算出函数在(x1,f(x1))处的函数值增量
Δf= f(x1+Δx)-f(x1),这是解题的关键.
?
解:∵ f(x)=2x2+3x-5,
∴ Δf=f(x1+Δx)-f(x1)=2(x1+Δx)2+3(x1+Δx)-5-(2????12+3x1-5)
=2[(Δx)2+2x1Δx]+3Δx=2(Δx)2+(4x1+3)Δx.
(1)当x1=4,且Δx=1时,Δf=2+(4×4+3)=21,????????????????=211=21.
(2)当x1=4,且Δx=0.1时,Δf=2×0.12+(4×4+3)×0.1=0.02+1.9=1.92.
????????????????=1.920.1=19.2.
(3)在(1)中,????????????????=????????2?????????1????2?????1=????5?????45?4,它表示过抛物线上的点(4,39)
与点(5,60)的直线的斜率.
在(2)中,????????????????=????????2?????????1????2?????1=????4.1?????44.1?4,它表示过抛物线上的点(4,39)与
点(4.1,40.92)的直线的斜率.
点评:求函数的平均变化率时要准确计算出函数在(x1,f(x1))处的函数值增量
Δf= f(x1+Δx)-f(x1),这是解题的关键.
?
例2 汽车行驶的路程s和时间t之间的函数图像如图所示,在时间段
[0,t1],[t1,t2],[t2,t3]上的平均速度分别为v1,v2,v3,
三者的大小关系为 .
解析 由题意,可得v1=????????1?????0????1?0=kOA,v2=????????2?????????1????2?????1=kAB,v3=????????3?????????2????3?????2=kBC.
由题图可得kBC>kAB>kOA,所以v3>v2>v1.
答案 v3>v2>v1
点评 本题主要考查了函数平均变化率的应用,其中由平均变化率的意义,求得v1,v2,v3的表达式,利用直线的斜率作出比较是解答本题的关键,着重考查了分析问题和解决问题的能力,以及推理能力.
?
例3已知函数f(x)=2????在区间[1,t]上的平均变化率为-23,则t= .
解析 ∵ 函数y=2????在区间[1,t]上的平均变化率为-2????,∴ -2????=?23,解得t=3.
答案 3
点评 此题先计算出函数y=2????在区间[1,t]上的平均变化率为-2????,再由平均变化率为?23,得出结果.
?
课堂小结
知识清单:
平均变化率;平均变化率的意义;平均变化率的求法.
方法归纳:平均变化率的求法:作差求自变量的增量→作差求函数值的增量→作商求平均变化率
常见误区:容易误解函数值的该变量,要区分好Δx与Δy.
谢 谢!
6.1
导数
6.1.1 函数的平均变化率
学习目标
核心素养:数学抽象、直观想象、数学运算
1.理解函数平均变化率的概念,会用对应的符号语言刻画函数的平均变化率;了解函数平均变化率的几何意义.
2.会求函数的平均变化率;理解函数平均变化率的模型.
3.理解符号“????????????????”的含义.
?
新知学习
情境与问题
药物在动物体内的含量随时间变化的规律,是药学与数学之间的边缘学科——药物动力学的研究内容,相关的规律是确定药物的使用量和用药时间间隔的依据.他克莫司是一种新型免疫抑制剂,在器官移植临床中的应用非常广泛.已知某病人服用他克莫司t h后血药浓度w μg/L的一些对应数据如下表所示.
(1)当t∈[0.5,1]和t∈[1,1.5]时,w都是增加的,哪个时间段w的增加更快?
(2)当t∈[3,5]时,平均每小时w的变化量为多少?这里的平均每小时的变化量有什么实际意义?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t
0
0.5
1
1.5
2
3
5
8
w
0
6.6
28.6
39.1
31
22.7
8.8
8.3
提示解读
由所给数据不难看出,当t∈[0.5,1]和t∈[1,1.5]时,w的增加量分别为
28.6-6.6=22,39.1-28.6=10.5,
因为时间间隔都是0.5 h,所以t∈[0.5,1]时,w增加更快.
当t∈[3,5]时,w的变化量为
8.8-22.7=-13.9 ,
又因为共有5-3=2(h),所以平均每小时的变化量为?13.92=-6.95.这说明,在[3,5]这段时间内,任意1个小时血药浓度平均减少6.95 μg/L,此时,任意h(h∈[0,2])个小时血药浓度平均减少6.95 h μg/L.
?
总结归纳:函数的平均变化率
1.定义
一般地,若函数y=f(x)的定义域为D,且
x1,x2∈D,x1≠x2,y1=f(x1),y2=f(x2),
则称Δx=x2-x1为自变量的改变量;
称Δy=y2-y1(或Δf=f(x2)-f(x1))为相应的因变量的改变量;
称????????????????=????2?????1????2?????1或????????????????=????????2?????????1????2?????1 为函数y=f(x)在以x1,x2为端点的闭区间上的平均变化率,
其中“以x1,x2为端点的闭区间”,在x1
2.意义
平均变化率的实际意义是,在以x1,x2为端点的闭区间上,自变量每增加1个单位,因变量平均将增加????????????????个单位.因此,如果自变量增加h个单位,那么因变量将增加????????????????h个单位.
?
注意与提醒
(1)上述Δx在x1
f(x2)=f(x1+Δx),因此平均变化率
????????????????=????????1+?????????????????1????1+?????????????1=????????1+?????????????????1????????.
(2)函数在x=x0处有定义.
(3)x1是x0附近的任意一点,所以Δx=x1-x0≠0,但Δx可为正值,也可为负值.
(4)改变量的对应:若Δx=x1-x0,则Δf=f(x1)-f(x0),而不是Δf=f(x0)-f(x1).
?
3.图形表示
函数在一个区间内的平均变化率,等于这个区间端点对应的函数图像上两点连线的斜率.例如,图中函数y=f(x)在[x1,x2]上的平均变化率,等于直线AB的斜率,其中
A(x1,f(x1)),B(x2,f(x2)).
因此,平均变化率近似地刻画了函数对应的曲线(即函数图像)在某一区间上的变化趋势,是曲线倾斜程度的“数量化”,曲线的倾斜程度是平均变化率的“直观化”.
注意
(1)函数在x0到x0+Δx的平均变化率的几何意义是曲线y=f(x)过点(x0,f(x0)),(x0+Δx,f(x0+Δx))的割线的斜率,平均变化率刻画了函数f(x)的图像在x0附近的
陡峭程度,其绝对值越大,图像越陡,反之越平缓.
(2)平均变化率是曲线陡峭程度的“数量化”,曲线陡峭程度是平均变化率的“直观化”.利用平均变化率可以刻画变量平均变化的趋势和快慢程度,但效果是“粗糙不精确的”.
只有当Δx无限变小时,这种量化才由“粗糙”逼近“精确”.
求函数f(x)=x2在下列区间上的平均变化率.
(1)[1,3];
(2)以1和1+Δx为端点的闭区间.
即时巩固
解 (1)依定义可知
????????????????=????3?????13?1=32?122=4,
即f(x)在[1,3]上的平均变化率为4.
(2)依定义可知
????????????????=????1+?????????????1????????=1+????????2?12????????=2+Δx,
f(x)在以1和1+Δx为端点的闭区间上的平均变化率为 2+Δx .
?
4.以直代曲
将图中的线段AB近似地看成w在[3,5]上的图像.
用直线段代替了曲线段,这在数学中简称为“以直代曲”.
5.平均速度与平均变化率
从物理学中我们知道,平均速度可以刻画物体在一段时间内运动的快慢.如果物体运动的位移
x m与时间t s的关系为x=h(t),则物体在[t1,t2](t1
这就是说,物体在某段时间内的平均速度等于x=h(t)在该段时间内的平均变化率.
?
已知某物体运动的位移x m是时间t s的函数,而且t=0.1时,x=0.25;t=0.5时,x=2.25.
(1)求这个物体在时间段[0.1,0.5]内的平均速度;
(2)估计出t=0.2时物体的位移.
解 (1)所求平均速度为2.25?0.250.5?0.1=20.4=5(m/s).
(2)将x在[0.1,0.5]上的图像看成直线,则由(1)可知,直线的斜率为5,
且直线通过点(0.1,0.25),因此,x与t的关系可近似地表示为x-0.25=5(t-0.1).
在上式中令t=0.2,可求得x=0.75,即t=0.2时物体的位移可以估计为0.75 m.
?
即时巩固
典例剖析
例1 已知函数f(x)=2x2+3x-5.
(1)求当x1=4,且Δx=1时,函数增量Δf和平均变化率????????????????;
(2)求当x1=4,且Δx=0.1时,函数增量Δf和平均变化率????????????????;
(3)若设x2=x1+Δx,分析(1)(2)中的平均变化率的几何意义.
?
解:∵ f(x)=2x2+3x-5,
∴ Δf=f(x1+Δx)-f(x1)=2(x1+Δx)2+3(x1+Δx)-5-(2????12+3x1-5)
=2[(Δx)2+2x1Δx]+3Δx=2(Δx)2+(4x1+3)Δx.
(1)当x1=4,且Δx=1时,Δf=2+(4×4+3)=21,????????????????=211=21.
(2)当x1=4,且Δx=0.1时,Δf=2×0.12+(4×4+3)×0.1=0.02+1.9=1.92.
????????????????=1.920.1=19.2.
(3)在(1)中,????????????????=????????2?????????1????2?????1=????5?????45?4,它表示过抛物线上的点(4,39)
与点(5,60)的直线的斜率.
在(2)中,????????????????=????????2?????????1????2?????1=????4.1?????44.1?4,它表示过抛物线上的点(4,39)与
点(4.1,40.92)的直线的斜率.
点评:求函数的平均变化率时要准确计算出函数在(x1,f(x1))处的函数值增量
Δf= f(x1+Δx)-f(x1),这是解题的关键.
?
解:∵ f(x)=2x2+3x-5,
∴ Δf=f(x1+Δx)-f(x1)=2(x1+Δx)2+3(x1+Δx)-5-(2????12+3x1-5)
=2[(Δx)2+2x1Δx]+3Δx=2(Δx)2+(4x1+3)Δx.
(1)当x1=4,且Δx=1时,Δf=2+(4×4+3)=21,????????????????=211=21.
(2)当x1=4,且Δx=0.1时,Δf=2×0.12+(4×4+3)×0.1=0.02+1.9=1.92.
????????????????=1.920.1=19.2.
(3)在(1)中,????????????????=????????2?????????1????2?????1=????5?????45?4,它表示过抛物线上的点(4,39)
与点(5,60)的直线的斜率.
在(2)中,????????????????=????????2?????????1????2?????1=????4.1?????44.1?4,它表示过抛物线上的点(4,39)与
点(4.1,40.92)的直线的斜率.
点评:求函数的平均变化率时要准确计算出函数在(x1,f(x1))处的函数值增量
Δf= f(x1+Δx)-f(x1),这是解题的关键.
?
例2 汽车行驶的路程s和时间t之间的函数图像如图所示,在时间段
[0,t1],[t1,t2],[t2,t3]上的平均速度分别为v1,v2,v3,
三者的大小关系为 .
解析 由题意,可得v1=????????1?????0????1?0=kOA,v2=????????2?????????1????2?????1=kAB,v3=????????3?????????2????3?????2=kBC.
由题图可得kBC>kAB>kOA,所以v3>v2>v1.
答案 v3>v2>v1
点评 本题主要考查了函数平均变化率的应用,其中由平均变化率的意义,求得v1,v2,v3的表达式,利用直线的斜率作出比较是解答本题的关键,着重考查了分析问题和解决问题的能力,以及推理能力.
?
例3已知函数f(x)=2????在区间[1,t]上的平均变化率为-23,则t= .
解析 ∵ 函数y=2????在区间[1,t]上的平均变化率为-2????,∴ -2????=?23,解得t=3.
答案 3
点评 此题先计算出函数y=2????在区间[1,t]上的平均变化率为-2????,再由平均变化率为?23,得出结果.
?
课堂小结
知识清单:
平均变化率;平均变化率的意义;平均变化率的求法.
方法归纳:平均变化率的求法:作差求自变量的增量→作差求函数值的增量→作商求平均变化率
常见误区:容易误解函数值的该变量,要区分好Δx与Δy.
谢 谢!
