高中数学选择性必修第三册RJ·B--6.1 导数-6.1.2 导数及其几何意义 课件(共36张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·B--6.1 导数-6.1.2 导数及其几何意义 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 09:12:21 | ||
图片预览











文档简介
第六章
6.1
导数
6.1.2 导数及其几何意义
学习目标
1.了解瞬时速度的概念,了解导数的实际背景,理解导数的概念,体会导数的思想及其内涵.
2.会应用定义求简单函数的导数.
3.掌握导数的几何意义,会求曲线的切线方程.
4.掌握导数几何意义的简单应用.
核心素养:数学抽象、直观想象、数学运算
新知学习
在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.进一步地,能否精确定量地刻画变化速度的快慢呢?下面我们就来研究这个问题.
新知学习
在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.进一步地,能否精确定量地刻画变化速度的快慢呢?下面我们就来研究这个问题.
问题探究
直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动得越来越慢,在下降阶段运动得越来越快.我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度????近似地描述他的运动状态.
例如,在0≤????≤0.5这段时间里,????=?0.5??(0)0.5?0=2.35(m/s);
在1≤t≤2这段时间里,????=?2??(1)2?1=?9.9(m/s).
一般地,在????1≤????≤????2这段时间里,
????=?????2??(????1)????2?????1=?4.9(????1+????2)+4.8.
?
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度?(单位:m)
与起跳后的时间????(单位:s)存在函数关系?(????)=?4.9????2+4.8????+11.
如何描述运动员从起跳到入水的过程中运动的快慢程度呢?
?
思考:计算运动员在0≤????≤4849这段时间里的平均速度,你发现了什么?你认为用平均速度描述运动员的运动状态有什么问题吗?
?
我们发现,运动员在0≤????≤4849这段时间里的平均速度为0.显然,在这段时间内,运动员并不处于静止状态.因此,用平均速度不能准确反映运动员在这一时间段里的运动状态.
?
为了精确刻画运动员的运动状态,需要引入瞬时速度的概念.
我们把物体在某一时刻的速度称为瞬时速度.
探究:瞬时速度与平均速度有什么关系?你能利用这种关系求运动员在????=1?????时的瞬时速度吗?
?
设运动员在????0时刻附近某一时间段内的平均速度是????,可以想象,如果不断缩短这一时间段的长度,那么????将越来越趋近于运动员在????0时刻的瞬时速度.
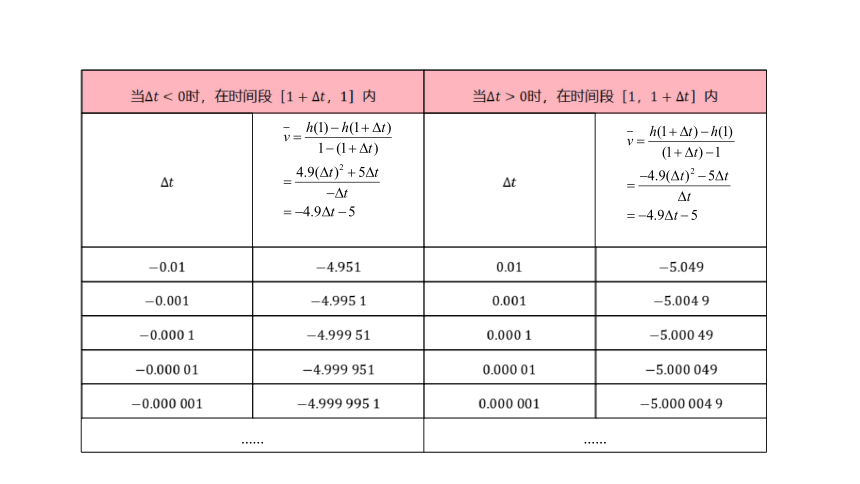
为了求运动员在????=1时的瞬时速度,我们在????=1之后或之前,任意取一个时刻1+Δ????,Δ????是时间改变量,可以是正值,也可以是负值,但不为0.当Δ????>0时,1+Δ????在1之后;当Δ????<0时,1+Δ????在1之前.当Δ????>0时,把运动员在时间段[1,1+Δ????]内近似看成做匀速直线运动,计算时间段[1,1+Δ????]内的平均速度????,用平均速度????近似表示运动员在????=1时的瞬时速度.当Δ????<0时,在时间段[1+Δ????,1]内可作类似处理.为了提高近似表示的精确度,我们不断缩短时间间隔,得到如下表格
?
当Δ????<0时,在时间段[1+Δ????,1]内
当Δ????>0时,在时间段[1,1+Δ????]内
Δ????
?
Δ????
?
?0.01
?4.951
0.01
?5.049
?0.001
?4.995?1
0.001
?5.004?9
?0.000?1
?4.999?51
0.000?1
?5.000?49
?0.000?01
?4.999?951
0.000?01
?5.000?049
?0.000?001
?4.999?995?1
0.000?001
?5.000?004?9
……
……
?
?
……
……
给出Δ????更多的值,我们可以利用计算工具计算对应的平均速度????的值,可以发现当Δ????无限趋近于0,即无论????从小于1的一边,还是从大于1的一边无限趋近于1时,平均速度????都无限趋近于?5.
?
当Δ????无限趋近于0时,?4.9Δ????也无限趋近于0,所以????无限趋近于?5.这与前面得到的结论一致.
?
事实上,由 可以发现,
数学中,我们把?5叫做“当Δ????无限趋近于0时, 的极限”,记为
?
从物理的角度看,当时间间隔|Δ????|无限趋近于0时,平均速度????就无限趋近于????=1时的瞬时速度.因此,运动员在????=1s?时的瞬时速度????(1)=?5?m/s.
?
或当Δ????→0时,
?
1.定义
一般地,设函数y=f(x)在x0附近①有定义,自变量在x=x0处的改变量为Δx,当Δx无限接近于0时,若平均变化率????????????????=????????????+?????????????????????????????无限接近于一个常数k,那么称常数k为函数f(x)在x=x0处的瞬时变化率.
此时,也称f(x)在x0处可导,并称k为f(x)在x=x0处的导数,记作f ′(x0)=k.
为了简单起见,“当Δx无限接近于0时,????????0+?????????????????0????????无限接近于常数k”也常用符号“→”(读作“趋向于”)表示为
当Δx→0时,????????0+?????????????????0????????→k,或者写成lim????????→0????????0+?????????????????0????????=k,
即
f ′(x0)=lim????????→0????????0+?????????????????0????????.????
?
总结归纳:瞬时变化率与导数
2.瞬时变化率的意义
由f ′(x0)=lim????????→0????????0+?????????????????0????????.?式还可以看出,当Δx很小时,f ′(x0)≈????????0+?????????????????0????????,从而
f(x0+Δx)-f(x0)≈f ′(x0)Δx.
由此能得到瞬时变化率f ′(x0)的实际意义:当自变量在x=x0处的改变量Δx很小时,因变量对应的改变量的近似值为f ′(x0)Δx.
?
注意事项
(1)平均变化率反映的是函数在某一区间的性质,而瞬时变化率反映的是函数在某一个点的性质.
(2)平均变化率随Δx的变化而变化,瞬时变化率是一个常量,它不随Δx的变化而变化.
归纳提升
(1)函数f(x)在x=x0处有导数,也说f(x)在x=x0处可导,f(x)在x=x0处可导必须满足f(x)在x0及其附近有定义.
(2)f(x)在x0处可导,指Δx→0时,????????????????→k(常数).
(3)由导数的定义知求函数y=f(x)在点x0处的导数的步骤:
①求函数值的增量Δf=f(x0+Δx)-f(x0);
②求平均变化率????????????????=????????0+?????????????????0????????;
③取极限,得导数f ′(x0)=lim????????→0????????????????(或当Δx→0时,????????????????→f ′(x0)).
(4)函数f(x)在x=x0处的导数定义的等价形式:函数f(x)在x=x0处的导数定义的结构形式为f ′(x0)=lim????????→0????????0+?????????????????0????????.现在令x=x0+Δx,则x-x0=Δx,当Δx→0时,x-x0→0,即x→x0,因此,函数f(x)在x=x0处的导数可表示为f ′(x0)=lim????????→0?????????????????0?????????0.
?
1.已知函数f(x)=-x2,求f(x)在x=3处的导数f ′(3).
解 当自变量在x=3处的改变量为Δx时,平均变化率
????????????????=????3+?????????????3????????=?3+????????2??32????????=-6-Δx.
可以看出,当Δx无限接近于0时,????????????????无限接近于-6,因此
f ′(3)=lim????????→0????3+?????????????3????????=lim????????→0(-6-Δx)=-6.
?
即时巩固
2.在生产过程中,产品的总成本C一般来说是产量Q的函数,记作C=f(Q),称为总成本函数.为了方便起见,经济学家一般假设Q能在某一区间内连续地取值,并将总成本函数在Q0处的导数f ′(Q0)称为在Q0处的边际成本,用MC(Q0)表示,即MC(Q0)=f ′(Q0).
已知某产品的总成本函数为C=Q2,求边际成本MC(300),并说明其实际意义.
解 设Q=300时产量的改变量为ΔQ,则
????????????????=300+????????2?3002????????=600+ΔQ .
令ΔQ→0,可得MC(300)=600 .
因此,产量为300时的边际成本为600.其实际意义是:此时多生产1件产品,成本要增加600.
?
即时巩固
尝试与发现
已知函数f(x)=x2+x,设自变量在x=0处的改变量为Δx.
(1)依照定义求出f ′(0);
(2)设M(0+Δx,f(0+Δx))为函数图像上一点,探讨Δx无限接近于0时,直线OM具有什么样的性质.
提示
平均变化率????????????????=????0+?????????????0????????=0+????????2+0+?????????02+0????????=1+Δx.
可以看出,当Δx无限接近于0时,????????????????无限接近于1,因此
f ′(0)=lim????????→0????0+?????????????0????????=lim????????→0(1+Δx)=1.
?
观察 : 如图,当点????,????,????,????对应的Δ????趋近0时,直线OA,OB,OC,OD的斜率有什么变化趋势?
?
我们发现,点A,B对应的Δx都小于0,而且B对应的Δx更加接近于0,这也就是说,直线OA,OB的斜率都小于1,且OB的斜率更接近于1;类似地,点C,D对应的Δx都大于0,而且C对应的Δx更加接近于0,直线OC,OD的斜率都大于1,且OC的斜率更接近于1.趋近为同一条直线l.
这个确定位置的直线l为抛物线在点????处的切线.
?
总结归纳
1.如图所示,设S是平面上的一条曲线,P0是曲线S上的一个定点,P是曲线S
上P0附近的点,则称直线PP0为曲线S的割线,如果P无限接近于P0时,割线
PP0无限接近于通过P0的一条直线l,则称直线l为曲线S在点P0处的切线.
2.依照切线的定义可知,如果将函数y=f(x)的图像看成曲线(称为曲线y=f(x),下同),而且曲线在点A(x0,f(x0))处的切线为l,则Δx很小时,B(x0+Δx,f(x0+Δx))是A附近的一点,割线AB的斜率是
????????????????=????????0+?????????????????0????????,
则当Δx无限接近于0时,割线的斜率将无限趋近于切线l的斜率.
?
思考
以前初中学过的曲线在某点处切线的定义是什么?与此处切线的定义有什么不同?
提示:初中我们学习过圆的切线:直线和圆有唯一的公共点时,称直线和圆相切,唯一的公共点叫做切点,直线叫做圆的切线.但因为圆是一种特殊的曲线,所以圆的切线定义不适用于一般的曲线.如图中的曲线C,直线l1与曲线C有唯一的公共点M,但l1不是曲线C的切线;l2虽然与曲线C有不止一个公共点,但l2是曲线C在点N处的切线.
导数的几何意义
f ′(x0)就是曲线y=f(x)在点(x0,f(x0))处(也称在x=x0处)的切线的斜率,从而根据直线的点斜式方程可知,切线的方程是
y-f(x0)=f ′(x0)(x-x0).
总结
(1)若函数y=f(x)在点x0处可导,则其图像在该点处必有切线,其切点为(x0,f(x0)),斜率为f ′(x0),切线方程为y-f(x0)=f ′(x0)(x-x0).
(2)曲线f(x)在点(x0,f(x0))处有切线,但函数f(x)在该点处不一定可导,如f(x)=????在x=0处有切线,但在x=0处不可导.
(3)若曲线y=f(x)在点P(x0,f(x0))处的导数不存在,但曲线在该点处有切线,则切线与x轴垂直.
(4)显然f ′(x0)>0,切线的倾斜角为锐角;f ′(x0)<0,切线的倾斜角为钝角;f ′(x0)=0,切线与x轴平行.
?
求抛物线????(????)=????2+3?????2在点(1,2)处的切线方程.
?
解: 抛物线????(????)=????2+3?????2在点(1,2)处的切线斜率
?
所以,抛物线????(????)=????2+3?????2在点(1,2)处的切线方程为
?????2=5(?????1),即5??????????3=0.
?
即时巩固
以“以直代曲”从几何上理解瞬时变化率
如果函数y=f(x)在x0处的导数为f ′(x0),且在x0处自变量的改变量为Δx,对应的函数值改变量为
Δy=f(x0+Δx)-f(x0),则f(x0+Δx)=f(x0)+Δy.
如图所示,此时曲线y=f(x)在x0处的切线l的斜率为f ′(x0),
因此AC=Δx,CD=f ′(x0)Δx.
又因为BC=Δy,可以看出,当Δx很小时,Δy可用 f ′(x0)Δx来近似表示,
即Δy≈f ′(x0)Δx,
因此f(x0+Δx)≈f(x0)+f ′(x0)Δx.
这就说明,在x=x0的附近,自变量的改变量Δx很小时,因变量改变量的近似值为 f ′(x0)Δx,这与前面所说的瞬时变化率的实际意义是相同的.此时,也就能用f(x0),f ′(x0)和Δx的值来得到f(x0+Δx)的近似值,而且Δx越小,近似效果越好.这种求近似值的方法,本质上是用x=x0处的切线代替了x=x0附近的曲线y=f(x),因此也是使用了“以直代曲”的方法.
典例剖析
例1 已知质点M做直线运动,且位移s(单位:cm)随时间t(单位:s)变化的函数为s=2t2+3.
(1)当t=2,Δt=0.01时,求????????????????;
(2)当t=2,Δt=0.001时,求????????????????;
(3)求质点M在t=2时的瞬时速度.
?
解题提示 Δs即位移的改变量,Δt即时间的改变量,????????????????即平均速度;Δt越小,求出的????????????????越接近某时刻的瞬时速度.
解 ???????????????????????=????????+?????????????????????????=2????+????????2+3?2????2+3????????=4t+2Δt.
(1)当t=2,Δt=0.01时,????????????????=4×2+2×0.01=8.02.
(2)当t=2,Δt=0.001时,????????????????=4×2+2×0.001=8.002.
(3)当t=2时,lim????????→0????????????????=lim????????→0(4t+2Δt)=4t=4×2=8,即质点M在t=2时的瞬时速度为8 cm/s.
?
类题通法
求瞬时速度的步骤
(1)设非匀速直线运动的规律为函数s=s(t);
(2)写出时间改变量Δt,位移改变量Δs=s(t0+Δt)-s(t0);
(3)求得平均速度????=????????????????;
(4)求瞬时速度v:当Δt→0时,????????????????→v(常数).
?
例2 如图,函数y=f(x)的图像在点P处的切线方程是y=-2x+9,点P的横坐标是4,
则f(4)+f ′(4)= .
解析 ∵ 函数f(x)的图像在点P处的切线为y=-2x+9,
∴ k切=-2=f ′(4).
又∵ f(4)=1,
∴ f(4)+f ′(4)=-1.
答案 -1
例3 若函数y=f(x)在x=x0处可导,则lim?→0????????0+??????????0???等于 ( )
A.f ′(x0) B.2f ′(x0) C.-2f ′(x0) D.0
?
解析 (方法1)lim?→0????????0+??????????0???=lim?→0????????0+??????????0+????????0?????????0???=lim?→0????????0+??????????0?+lim?→0????????0?????????0???
=f ′(x0)+lim?→0????????0+???????????0??=f ′(x0)+f ′(x0)=2f ′(x0).
(方法2)lim?→0????????0+??????????0???=lim?→02×????????0+??????????0??2?=2lim?→0????????0+??????????0??2?=2f ′(x0).
答案 B
点评:导数的形式化计算,其本质就是对导数f ′(x0)=lim????????→0????????0+?????????????????0????????=lim????→????0?????????????????0?????????0的理解.需要说明的是,导数是一个局部概念,它只与函数y=f(x)在x=x0及其附近的函数值有关,与Δx无关.
?
例4 已知f(x)=x+1????,求f ′(1).
?
解 (方法1)∵ Δf=(1+Δx)+11+?????????1+11=Δx+11+????????-1=Δx+?????????1+????????=Δx-????????1+????????,
∴????????????????=1-11+????????,
∴ f ′(1)=lim????????→01?11+????????=0.
(方法2)f ′(x)=lim????????→0????????+?????????????????????????=lim????????→0????+????????+1????+??????????????1????????????=lim????????→01?1????????+????????=1-1????2,
∴ 当x=1时,f ′(1)=0.
?
类题通法
用导数的定义来求一个函数的导数,一般分三步:
①求Δf=f(x+Δx)-f(x);
②求????????????????=????????+?????????????????????????;
③求lim????????→0????????????????.(即一差、二比、三极限)
?
例5 求曲线f(x)=x2+1????-3在x=2处的切线方程.
?
解 ∵ Δf=f(2+Δx)-f(2)=(2+Δx)2+12+????????-3-22+12?3=4Δx+(Δx)2+12+????????-12=4Δx+(Δx)2-????????22+????????,
∴????????????????=4+Δx-122+????????.
∵ 当Δx→0时,????????????????→4-14=154,
∴ 曲线在x=2处的切线斜率为154.
又x=2时,f(2)=32,
∴ 切点坐标为2,32.
∴ 曲线在x=2处的切线方程为y-32=154(x-2),
即15x-4y-24=0.
?
类题通法
求曲线y=f(x)在其上一点P(x0,y0)处的切线方程的方法
1.若曲线y=f(x)在点P(x0,y0)处的切线的斜率存在,则斜率k=f ′(x0),切线方程为y-y0=f ′(x0)·(x-x0).
2.若曲线y=f(x)在点P(x0,y0)处的切线斜率不存在,则切线方程为x=x0,此时f ′(x0)也不存在.
例6 已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值.
解 f ′(1)=lim????????→0????1+?????????????1????????=lim????????→0????1+????????2+1??????1????????=2a,
g′(1)=lim????????→0????1+?????????????1????????=lim????????→01+????????3+????1+?????????1?????????????=lim????????→03????????+3????????2+????????3+????????????????????=3+b.
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,
所以f(1)=g(1),且f ′(1)=g ′(1).
即????+1=1+????,2????=3+????,解得????=3,????=3.
规律总结:求与曲线的切线有关的参数问题,解题的关键是灵活运用导数的几何意义,利用方程思想求解.
?
类题通法
求曲线y=f(x)在其上一点P(x0,y0)处的切线方程的方法
1.若曲线y=f(x)在点P(x0,y0)处的切线的斜率存在,则斜率k=f ′(x0),切线方程为y-y0=f ′(x0)·(x-x0).
2.若曲线y=f(x)在点P(x0,y0)处的切线斜率不存在,则切线方程为x=x0,此时f ′(x0)也不存在.
随堂小测
1. 若曲线f(x)=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则 ( )
A.a=1,b=1 B.a=-1,b=1 C.a=1,b=-1 D.a=-1,b=-1
2. 已知函数f(x)在x0附近有定义,且有f(x0+Δx)-f(x0)=aΔx+b(Δx)2,其中a,b为常数,则下列说法正确的是( )
A.f ′(x)=a B.f ′(x)=b C.f ′(x0)=a D.f ′(x0)=b
3.设f(x)满足lim????????→0????1?????1?????????2????????=-1,则曲线y=f(x)上点(1,f(1))处的切线斜率为 .
4.小华在参加一次同学聚会时,他用如图所示的圆口杯喝饮料,小华认为:如果向杯子中倒饮料的速度一定(即单位时间内倒入的饮料量相同),那么杯子中饮料的高度h是关于时间t的函数h(t),则函数h(t)的图像可能是( )
?
?????
A
C
-2
B
A
B
C
D
5.已知直线l:y=4x+a和曲线C:y=x3-2x2+3相切,求实数a的值及切点的坐标.
解 设直线l与曲线C相切于点P(x0,y0),
f ′(x0)=lim????????→0????????0+?????????????????0????????=lim????????→0????0+????????3?2????0+????????2+3?????03?2????02+3????????=3????02-4x0.
由题意可知l的斜率k=4,
令3????02-4x0=4,解得x0=-23或2.
∴ 切点的坐标为?23,4927或(2,3).
当切点坐标为?23,4927时,有4927=4×?23+a,解得a=12127.
当切点坐标为(2,3)时,有3=4×2+a,解得a=-5.
综上所述,当切点坐标为?23,4927时,a=12127;
当切点坐标为(2,3)时,a=-5.
?
6.已知直线l1为曲线y=x2+x-2在点(1,0)处的切线,直线l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1,l2和x轴所围成的三角形的面积.
解 (1)令f(x)=x2+x-2.由题意知f ′(1)=lim????????→01+????????2+1+?????????2?0????????=3.
设直线l2与曲线的切点为P(x0,????02 +x0-2),则f ′(x0)=lim????????→0????0+????????2+????0+?????????2?????02+????0?2????????=2x0+1,
则直线l2的方程为y-(????02+x0-2)=(2x0+1)(x-x0).
∵ l1⊥l2,∴ 3(2x0+1)=-1,∴ x0=-23,∴ 直线l2的方程为y=-13x-229.
(2)由(1)可得直线l1的方程为y=3x-3,解方程组????=3?????3,????=?13?????229,得????=16,????=?52.
又∵ 直线l1,l2与x轴的交点坐标分别为(1,0),?223,0,
∴ 所围成的三角形的面积为12×?52×1+223=12512.
?
课堂小结
知识清单:
瞬时变化率;导数的定义;导数的几何意义;求切线方程.
方法归纳:求曲线在某一点处的切线方程的方法.
常见误区:求曲线在某一点处的切线方程要注意,切线斜率是否存在要进行讨论.
谢 谢!
6.1
导数
6.1.2 导数及其几何意义
学习目标
1.了解瞬时速度的概念,了解导数的实际背景,理解导数的概念,体会导数的思想及其内涵.
2.会应用定义求简单函数的导数.
3.掌握导数的几何意义,会求曲线的切线方程.
4.掌握导数几何意义的简单应用.
核心素养:数学抽象、直观想象、数学运算
新知学习
在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.进一步地,能否精确定量地刻画变化速度的快慢呢?下面我们就来研究这个问题.
新知学习
在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识定性地研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长”是越来越慢的,“指数爆炸”比“直线上升”快得多.进一步地,能否精确定量地刻画变化速度的快慢呢?下面我们就来研究这个问题.
问题探究
直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动得越来越慢,在下降阶段运动得越来越快.我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度????近似地描述他的运动状态.
例如,在0≤????≤0.5这段时间里,????=?0.5??(0)0.5?0=2.35(m/s);
在1≤t≤2这段时间里,????=?2??(1)2?1=?9.9(m/s).
一般地,在????1≤????≤????2这段时间里,
????=?????2??(????1)????2?????1=?4.9(????1+????2)+4.8.
?
在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度?(单位:m)
与起跳后的时间????(单位:s)存在函数关系?(????)=?4.9????2+4.8????+11.
如何描述运动员从起跳到入水的过程中运动的快慢程度呢?
?
思考:计算运动员在0≤????≤4849这段时间里的平均速度,你发现了什么?你认为用平均速度描述运动员的运动状态有什么问题吗?
?
我们发现,运动员在0≤????≤4849这段时间里的平均速度为0.显然,在这段时间内,运动员并不处于静止状态.因此,用平均速度不能准确反映运动员在这一时间段里的运动状态.
?
为了精确刻画运动员的运动状态,需要引入瞬时速度的概念.
我们把物体在某一时刻的速度称为瞬时速度.
探究:瞬时速度与平均速度有什么关系?你能利用这种关系求运动员在????=1?????时的瞬时速度吗?
?
设运动员在????0时刻附近某一时间段内的平均速度是????,可以想象,如果不断缩短这一时间段的长度,那么????将越来越趋近于运动员在????0时刻的瞬时速度.
为了求运动员在????=1时的瞬时速度,我们在????=1之后或之前,任意取一个时刻1+Δ????,Δ????是时间改变量,可以是正值,也可以是负值,但不为0.当Δ????>0时,1+Δ????在1之后;当Δ????<0时,1+Δ????在1之前.当Δ????>0时,把运动员在时间段[1,1+Δ????]内近似看成做匀速直线运动,计算时间段[1,1+Δ????]内的平均速度????,用平均速度????近似表示运动员在????=1时的瞬时速度.当Δ????<0时,在时间段[1+Δ????,1]内可作类似处理.为了提高近似表示的精确度,我们不断缩短时间间隔,得到如下表格
?
当Δ????<0时,在时间段[1+Δ????,1]内
当Δ????>0时,在时间段[1,1+Δ????]内
Δ????
?
Δ????
?
?0.01
?4.951
0.01
?5.049
?0.001
?4.995?1
0.001
?5.004?9
?0.000?1
?4.999?51
0.000?1
?5.000?49
?0.000?01
?4.999?951
0.000?01
?5.000?049
?0.000?001
?4.999?995?1
0.000?001
?5.000?004?9
……
……
?
?
……
……
给出Δ????更多的值,我们可以利用计算工具计算对应的平均速度????的值,可以发现当Δ????无限趋近于0,即无论????从小于1的一边,还是从大于1的一边无限趋近于1时,平均速度????都无限趋近于?5.
?
当Δ????无限趋近于0时,?4.9Δ????也无限趋近于0,所以????无限趋近于?5.这与前面得到的结论一致.
?
事实上,由 可以发现,
数学中,我们把?5叫做“当Δ????无限趋近于0时, 的极限”,记为
?
从物理的角度看,当时间间隔|Δ????|无限趋近于0时,平均速度????就无限趋近于????=1时的瞬时速度.因此,运动员在????=1s?时的瞬时速度????(1)=?5?m/s.
?
或当Δ????→0时,
?
1.定义
一般地,设函数y=f(x)在x0附近①有定义,自变量在x=x0处的改变量为Δx,当Δx无限接近于0时,若平均变化率????????????????=????????????+?????????????????????????????无限接近于一个常数k,那么称常数k为函数f(x)在x=x0处的瞬时变化率.
此时,也称f(x)在x0处可导,并称k为f(x)在x=x0处的导数,记作f ′(x0)=k.
为了简单起见,“当Δx无限接近于0时,????????0+?????????????????0????????无限接近于常数k”也常用符号“→”(读作“趋向于”)表示为
当Δx→0时,????????0+?????????????????0????????→k,或者写成lim????????→0????????0+?????????????????0????????=k,
即
f ′(x0)=lim????????→0????????0+?????????????????0????????.????
?
总结归纳:瞬时变化率与导数
2.瞬时变化率的意义
由f ′(x0)=lim????????→0????????0+?????????????????0????????.?式还可以看出,当Δx很小时,f ′(x0)≈????????0+?????????????????0????????,从而
f(x0+Δx)-f(x0)≈f ′(x0)Δx.
由此能得到瞬时变化率f ′(x0)的实际意义:当自变量在x=x0处的改变量Δx很小时,因变量对应的改变量的近似值为f ′(x0)Δx.
?
注意事项
(1)平均变化率反映的是函数在某一区间的性质,而瞬时变化率反映的是函数在某一个点的性质.
(2)平均变化率随Δx的变化而变化,瞬时变化率是一个常量,它不随Δx的变化而变化.
归纳提升
(1)函数f(x)在x=x0处有导数,也说f(x)在x=x0处可导,f(x)在x=x0处可导必须满足f(x)在x0及其附近有定义.
(2)f(x)在x0处可导,指Δx→0时,????????????????→k(常数).
(3)由导数的定义知求函数y=f(x)在点x0处的导数的步骤:
①求函数值的增量Δf=f(x0+Δx)-f(x0);
②求平均变化率????????????????=????????0+?????????????????0????????;
③取极限,得导数f ′(x0)=lim????????→0????????????????(或当Δx→0时,????????????????→f ′(x0)).
(4)函数f(x)在x=x0处的导数定义的等价形式:函数f(x)在x=x0处的导数定义的结构形式为f ′(x0)=lim????????→0????????0+?????????????????0????????.现在令x=x0+Δx,则x-x0=Δx,当Δx→0时,x-x0→0,即x→x0,因此,函数f(x)在x=x0处的导数可表示为f ′(x0)=lim????????→0?????????????????0?????????0.
?
1.已知函数f(x)=-x2,求f(x)在x=3处的导数f ′(3).
解 当自变量在x=3处的改变量为Δx时,平均变化率
????????????????=????3+?????????????3????????=?3+????????2??32????????=-6-Δx.
可以看出,当Δx无限接近于0时,????????????????无限接近于-6,因此
f ′(3)=lim????????→0????3+?????????????3????????=lim????????→0(-6-Δx)=-6.
?
即时巩固
2.在生产过程中,产品的总成本C一般来说是产量Q的函数,记作C=f(Q),称为总成本函数.为了方便起见,经济学家一般假设Q能在某一区间内连续地取值,并将总成本函数在Q0处的导数f ′(Q0)称为在Q0处的边际成本,用MC(Q0)表示,即MC(Q0)=f ′(Q0).
已知某产品的总成本函数为C=Q2,求边际成本MC(300),并说明其实际意义.
解 设Q=300时产量的改变量为ΔQ,则
????????????????=300+????????2?3002????????=600+ΔQ .
令ΔQ→0,可得MC(300)=600 .
因此,产量为300时的边际成本为600.其实际意义是:此时多生产1件产品,成本要增加600.
?
即时巩固
尝试与发现
已知函数f(x)=x2+x,设自变量在x=0处的改变量为Δx.
(1)依照定义求出f ′(0);
(2)设M(0+Δx,f(0+Δx))为函数图像上一点,探讨Δx无限接近于0时,直线OM具有什么样的性质.
提示
平均变化率????????????????=????0+?????????????0????????=0+????????2+0+?????????02+0????????=1+Δx.
可以看出,当Δx无限接近于0时,????????????????无限接近于1,因此
f ′(0)=lim????????→0????0+?????????????0????????=lim????????→0(1+Δx)=1.
?
观察 : 如图,当点????,????,????,????对应的Δ????趋近0时,直线OA,OB,OC,OD的斜率有什么变化趋势?
?
我们发现,点A,B对应的Δx都小于0,而且B对应的Δx更加接近于0,这也就是说,直线OA,OB的斜率都小于1,且OB的斜率更接近于1;类似地,点C,D对应的Δx都大于0,而且C对应的Δx更加接近于0,直线OC,OD的斜率都大于1,且OC的斜率更接近于1.趋近为同一条直线l.
这个确定位置的直线l为抛物线在点????处的切线.
?
总结归纳
1.如图所示,设S是平面上的一条曲线,P0是曲线S上的一个定点,P是曲线S
上P0附近的点,则称直线PP0为曲线S的割线,如果P无限接近于P0时,割线
PP0无限接近于通过P0的一条直线l,则称直线l为曲线S在点P0处的切线.
2.依照切线的定义可知,如果将函数y=f(x)的图像看成曲线(称为曲线y=f(x),下同),而且曲线在点A(x0,f(x0))处的切线为l,则Δx很小时,B(x0+Δx,f(x0+Δx))是A附近的一点,割线AB的斜率是
????????????????=????????0+?????????????????0????????,
则当Δx无限接近于0时,割线的斜率将无限趋近于切线l的斜率.
?
思考
以前初中学过的曲线在某点处切线的定义是什么?与此处切线的定义有什么不同?
提示:初中我们学习过圆的切线:直线和圆有唯一的公共点时,称直线和圆相切,唯一的公共点叫做切点,直线叫做圆的切线.但因为圆是一种特殊的曲线,所以圆的切线定义不适用于一般的曲线.如图中的曲线C,直线l1与曲线C有唯一的公共点M,但l1不是曲线C的切线;l2虽然与曲线C有不止一个公共点,但l2是曲线C在点N处的切线.
导数的几何意义
f ′(x0)就是曲线y=f(x)在点(x0,f(x0))处(也称在x=x0处)的切线的斜率,从而根据直线的点斜式方程可知,切线的方程是
y-f(x0)=f ′(x0)(x-x0).
总结
(1)若函数y=f(x)在点x0处可导,则其图像在该点处必有切线,其切点为(x0,f(x0)),斜率为f ′(x0),切线方程为y-f(x0)=f ′(x0)(x-x0).
(2)曲线f(x)在点(x0,f(x0))处有切线,但函数f(x)在该点处不一定可导,如f(x)=????在x=0处有切线,但在x=0处不可导.
(3)若曲线y=f(x)在点P(x0,f(x0))处的导数不存在,但曲线在该点处有切线,则切线与x轴垂直.
(4)显然f ′(x0)>0,切线的倾斜角为锐角;f ′(x0)<0,切线的倾斜角为钝角;f ′(x0)=0,切线与x轴平行.
?
求抛物线????(????)=????2+3?????2在点(1,2)处的切线方程.
?
解: 抛物线????(????)=????2+3?????2在点(1,2)处的切线斜率
?
所以,抛物线????(????)=????2+3?????2在点(1,2)处的切线方程为
?????2=5(?????1),即5??????????3=0.
?
即时巩固
以“以直代曲”从几何上理解瞬时变化率
如果函数y=f(x)在x0处的导数为f ′(x0),且在x0处自变量的改变量为Δx,对应的函数值改变量为
Δy=f(x0+Δx)-f(x0),则f(x0+Δx)=f(x0)+Δy.
如图所示,此时曲线y=f(x)在x0处的切线l的斜率为f ′(x0),
因此AC=Δx,CD=f ′(x0)Δx.
又因为BC=Δy,可以看出,当Δx很小时,Δy可用 f ′(x0)Δx来近似表示,
即Δy≈f ′(x0)Δx,
因此f(x0+Δx)≈f(x0)+f ′(x0)Δx.
这就说明,在x=x0的附近,自变量的改变量Δx很小时,因变量改变量的近似值为 f ′(x0)Δx,这与前面所说的瞬时变化率的实际意义是相同的.此时,也就能用f(x0),f ′(x0)和Δx的值来得到f(x0+Δx)的近似值,而且Δx越小,近似效果越好.这种求近似值的方法,本质上是用x=x0处的切线代替了x=x0附近的曲线y=f(x),因此也是使用了“以直代曲”的方法.
典例剖析
例1 已知质点M做直线运动,且位移s(单位:cm)随时间t(单位:s)变化的函数为s=2t2+3.
(1)当t=2,Δt=0.01时,求????????????????;
(2)当t=2,Δt=0.001时,求????????????????;
(3)求质点M在t=2时的瞬时速度.
?
解题提示 Δs即位移的改变量,Δt即时间的改变量,????????????????即平均速度;Δt越小,求出的????????????????越接近某时刻的瞬时速度.
解 ???????????????????????=????????+?????????????????????????=2????+????????2+3?2????2+3????????=4t+2Δt.
(1)当t=2,Δt=0.01时,????????????????=4×2+2×0.01=8.02.
(2)当t=2,Δt=0.001时,????????????????=4×2+2×0.001=8.002.
(3)当t=2时,lim????????→0????????????????=lim????????→0(4t+2Δt)=4t=4×2=8,即质点M在t=2时的瞬时速度为8 cm/s.
?
类题通法
求瞬时速度的步骤
(1)设非匀速直线运动的规律为函数s=s(t);
(2)写出时间改变量Δt,位移改变量Δs=s(t0+Δt)-s(t0);
(3)求得平均速度????=????????????????;
(4)求瞬时速度v:当Δt→0时,????????????????→v(常数).
?
例2 如图,函数y=f(x)的图像在点P处的切线方程是y=-2x+9,点P的横坐标是4,
则f(4)+f ′(4)= .
解析 ∵ 函数f(x)的图像在点P处的切线为y=-2x+9,
∴ k切=-2=f ′(4).
又∵ f(4)=1,
∴ f(4)+f ′(4)=-1.
答案 -1
例3 若函数y=f(x)在x=x0处可导,则lim?→0????????0+??????????0???等于 ( )
A.f ′(x0) B.2f ′(x0) C.-2f ′(x0) D.0
?
解析 (方法1)lim?→0????????0+??????????0???=lim?→0????????0+??????????0+????????0?????????0???=lim?→0????????0+??????????0?+lim?→0????????0?????????0???
=f ′(x0)+lim?→0????????0+???????????0??=f ′(x0)+f ′(x0)=2f ′(x0).
(方法2)lim?→0????????0+??????????0???=lim?→02×????????0+??????????0??2?=2lim?→0????????0+??????????0??2?=2f ′(x0).
答案 B
点评:导数的形式化计算,其本质就是对导数f ′(x0)=lim????????→0????????0+?????????????????0????????=lim????→????0?????????????????0?????????0的理解.需要说明的是,导数是一个局部概念,它只与函数y=f(x)在x=x0及其附近的函数值有关,与Δx无关.
?
例4 已知f(x)=x+1????,求f ′(1).
?
解 (方法1)∵ Δf=(1+Δx)+11+?????????1+11=Δx+11+????????-1=Δx+?????????1+????????=Δx-????????1+????????,
∴????????????????=1-11+????????,
∴ f ′(1)=lim????????→01?11+????????=0.
(方法2)f ′(x)=lim????????→0????????+?????????????????????????=lim????????→0????+????????+1????+??????????????1????????????=lim????????→01?1????????+????????=1-1????2,
∴ 当x=1时,f ′(1)=0.
?
类题通法
用导数的定义来求一个函数的导数,一般分三步:
①求Δf=f(x+Δx)-f(x);
②求????????????????=????????+?????????????????????????;
③求lim????????→0????????????????.(即一差、二比、三极限)
?
例5 求曲线f(x)=x2+1????-3在x=2处的切线方程.
?
解 ∵ Δf=f(2+Δx)-f(2)=(2+Δx)2+12+????????-3-22+12?3=4Δx+(Δx)2+12+????????-12=4Δx+(Δx)2-????????22+????????,
∴????????????????=4+Δx-122+????????.
∵ 当Δx→0时,????????????????→4-14=154,
∴ 曲线在x=2处的切线斜率为154.
又x=2时,f(2)=32,
∴ 切点坐标为2,32.
∴ 曲线在x=2处的切线方程为y-32=154(x-2),
即15x-4y-24=0.
?
类题通法
求曲线y=f(x)在其上一点P(x0,y0)处的切线方程的方法
1.若曲线y=f(x)在点P(x0,y0)处的切线的斜率存在,则斜率k=f ′(x0),切线方程为y-y0=f ′(x0)·(x-x0).
2.若曲线y=f(x)在点P(x0,y0)处的切线斜率不存在,则切线方程为x=x0,此时f ′(x0)也不存在.
例6 已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值.
解 f ′(1)=lim????????→0????1+?????????????1????????=lim????????→0????1+????????2+1??????1????????=2a,
g′(1)=lim????????→0????1+?????????????1????????=lim????????→01+????????3+????1+?????????1?????????????=lim????????→03????????+3????????2+????????3+????????????????????=3+b.
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,
所以f(1)=g(1),且f ′(1)=g ′(1).
即????+1=1+????,2????=3+????,解得????=3,????=3.
规律总结:求与曲线的切线有关的参数问题,解题的关键是灵活运用导数的几何意义,利用方程思想求解.
?
类题通法
求曲线y=f(x)在其上一点P(x0,y0)处的切线方程的方法
1.若曲线y=f(x)在点P(x0,y0)处的切线的斜率存在,则斜率k=f ′(x0),切线方程为y-y0=f ′(x0)·(x-x0).
2.若曲线y=f(x)在点P(x0,y0)处的切线斜率不存在,则切线方程为x=x0,此时f ′(x0)也不存在.
随堂小测
1. 若曲线f(x)=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则 ( )
A.a=1,b=1 B.a=-1,b=1 C.a=1,b=-1 D.a=-1,b=-1
2. 已知函数f(x)在x0附近有定义,且有f(x0+Δx)-f(x0)=aΔx+b(Δx)2,其中a,b为常数,则下列说法正确的是( )
A.f ′(x)=a B.f ′(x)=b C.f ′(x0)=a D.f ′(x0)=b
3.设f(x)满足lim????????→0????1?????1?????????2????????=-1,则曲线y=f(x)上点(1,f(1))处的切线斜率为 .
4.小华在参加一次同学聚会时,他用如图所示的圆口杯喝饮料,小华认为:如果向杯子中倒饮料的速度一定(即单位时间内倒入的饮料量相同),那么杯子中饮料的高度h是关于时间t的函数h(t),则函数h(t)的图像可能是( )
?
?????
A
C
-2
B
A
B
C
D
5.已知直线l:y=4x+a和曲线C:y=x3-2x2+3相切,求实数a的值及切点的坐标.
解 设直线l与曲线C相切于点P(x0,y0),
f ′(x0)=lim????????→0????????0+?????????????????0????????=lim????????→0????0+????????3?2????0+????????2+3?????03?2????02+3????????=3????02-4x0.
由题意可知l的斜率k=4,
令3????02-4x0=4,解得x0=-23或2.
∴ 切点的坐标为?23,4927或(2,3).
当切点坐标为?23,4927时,有4927=4×?23+a,解得a=12127.
当切点坐标为(2,3)时,有3=4×2+a,解得a=-5.
综上所述,当切点坐标为?23,4927时,a=12127;
当切点坐标为(2,3)时,a=-5.
?
6.已知直线l1为曲线y=x2+x-2在点(1,0)处的切线,直线l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1,l2和x轴所围成的三角形的面积.
解 (1)令f(x)=x2+x-2.由题意知f ′(1)=lim????????→01+????????2+1+?????????2?0????????=3.
设直线l2与曲线的切点为P(x0,????02 +x0-2),则f ′(x0)=lim????????→0????0+????????2+????0+?????????2?????02+????0?2????????=2x0+1,
则直线l2的方程为y-(????02+x0-2)=(2x0+1)(x-x0).
∵ l1⊥l2,∴ 3(2x0+1)=-1,∴ x0=-23,∴ 直线l2的方程为y=-13x-229.
(2)由(1)可得直线l1的方程为y=3x-3,解方程组????=3?????3,????=?13?????229,得????=16,????=?52.
又∵ 直线l1,l2与x轴的交点坐标分别为(1,0),?223,0,
∴ 所围成的三角形的面积为12×?52×1+223=12512.
?
课堂小结
知识清单:
瞬时变化率;导数的定义;导数的几何意义;求切线方程.
方法归纳:求曲线在某一点处的切线方程的方法.
常见误区:求曲线在某一点处的切线方程要注意,切线斜率是否存在要进行讨论.
谢 谢!
