高中数学选择性必修第三册RJ·B--6.1 导数-6.1.3 基本初等函数的导数 课件(共30张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·B--6.1 导数-6.1.3 基本初等函数的导数 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览











文档简介
第六章
6.1
导数
6.1.3 基本初等函数的导数
学习目标
1.能用导数的定义求常数函数、幂函数的导数.
2.掌握几个常用函数的导数及其应用.
3.掌握基本初等函数的导数公式及其运用.
4.指数与对数函数的导数公式的区别与运用.
核心素养:数学运算、数学抽象
新知学习
尝试与发现
已知函数f(x)=x2,任取一实数x0,判断f(x)在x0处是否可导.如果可导,求出 f ′(x0),并观察f ′(x0)与x0的关系.
提示:设自变量在x=x0附近的改变量为Δx,则函数在以x0,x0+Δx为端点的闭区间上的平均变化率为 ????????????????=????????0+?????????????????0????????=????0+????????2?????02????????=2x0+Δx.
可以看出,当Δx无限接近于0时,平均变化率无限接近于2????0,因此f(x)在x0处可导,而且
f ′(x0)=lim????????→0????????0+?????????????????0????????=lim????????→0(2x0+Δx)=2x0.
显然,f ′(x0)随x0的变化而变化,而且x0的值确定之后,f ′(x0)也就确定了.
例如,x0=2时,f ′(2)=2×2=4;x0=-3时,f ′(-3)=2×(-3)=-6.
这就说明,f ′(x0)是x0的函数.
?
总结归纳
一般地,如果函数y=f(x)在其定义域内的每一点x都可导,则称f(x)可导.此时,对定义域内的每一个值x,都对应一个确定的导数f ′(x).于是,在f(x)的定义域内,f ′(x)是一个函数,这个函数通常称为函数y=f(x)的导函数,记作f ′(x)(或y′,????′????),即
f ′(x)=y′=????′????=????????????????????→????????????+?????????????????????????.
?
提示:导函数通常也简称为导数.本书后续内容中,除了特别声明指的是求某一点的导数之外,“求导数”均指的是“求导函数”
下面我们看下几个常用函数的导数
1.函数????(????)=????的导数
?
若f?(????)=????(如下图)表示路程关于时间的函数,则f?′(????)=0可以解释为某物体的瞬时速度始终为0,即一直处于静止状态.
?
f ′(x)=lim????????→0????????+?????????????????????????=lim????????→0?????????????????=lim????????→00=0.
?
2.函数????(????)=????的导数
?
若f?(????)=????(如下图)表示路程关于时间的函数,则f?′(????)=1可以解释为某物体做瞬时速度为1的匀速直线运动.
?
f ′(x)=lim????????→0????????+?????????????????????????=lim????????→0????+?????????????????????=lim????????→01=1.
?
3.函数????(????)=????2的导数
?
f?′(????)=2????表示函数f?(????)=????2的图象(如下图)上点(????,????)处切线的斜率为2????,说明随着????的变化,切线的斜率也在变化.另一方面,从导数作为函数在一点的瞬时变化率来看,f?′(????)=2????表明:当????<0时,随着????的增加,|f?′(????)|越来越小,f?(????)=????2减少得越来越慢;当????>0时,随着????的增加,|f?′(????)|越来越大,f?(????)=????2增加得越来越快.若f?(????)=????2表示路程关于时间的函数,则f?′(????)=2????可以解释为某物体做变速运动,它在时刻x的瞬时速度为2????.
?
4.函数????(????)=????3 的导数
?
????′(????)=3????2表示函数????(????)=????3的图象(如下图)上点(????,????)处切线的斜率为3????2,这说明随着????的变化,切线的斜率也在变化,且恒为非负数.
?
f ′(x)=lim????????→0????????+?????????????????????????=lim????????→0????+????????3?????3????????
=lim????????→0[3x2+3xΔx+(Δx)2]=3x2.
?
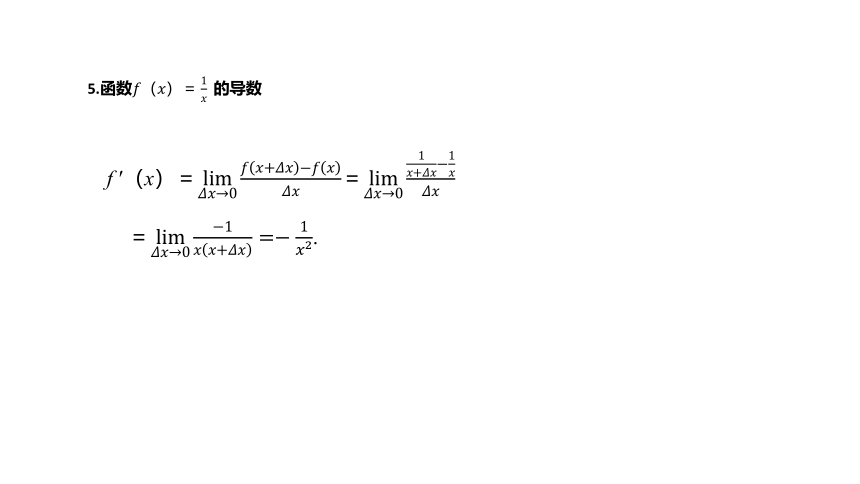
5.函数????(????)=1?????的导数
?
f ′(x)=lim????????→0????????+?????????????????????????=lim????????→01????+?????????1????????????
?=lim????????→0?1????????+????????=?1????2.
?
探究:画出函数????(????)=1?????的图象.根据图象,描述它的变化情况,并求出曲线在点(1,1)
处的切线方程.
?
函数????(????)=1?????的图象如图所示,
函数????(????)=1????的导数为????′(????)=1????′=?1????2-.
结合函数????(????)=1????的图象可以发现:
当????<0时,函数值????(????)随着????的增加,减少得越来越快;
当????>0时,函数值????(????)随着????的增加,减少得越来越慢.
曲线????(????)=1????在点(1,1)处的切线的斜率就是导函数????′(????)=?1????2在????=1处的函数值,即切线的斜率为?1,
故曲线y= ????(????)在点(1,1)处的切线方程为y=?????+2,
?
6.函数????(????)=???? 的导数
?
说明:前面我们根据导数的定义求出了一些常用函数的导数,这些函数都是幂函数????(????)=????????的形式,在以后求导数时,可直接应用上述常见函数的导数,不必再用定义去求导.
?
总结归纳
(1)对常见幂函数的导数及任意幂函数y=xα的求导都要重点背.
(2)函数y=C,y=x,y=x2,y=x3,y=?????1,y=????12的导数以及幂函数y=xα的求导公式,在以后的求导中可以直接运用,不必再利用导数定义去求,但要理解其推导过程.
(3)对不能直接运用公式的要适当进行变形,如y=1????7=?????7,y=5????2=????25等(即对于y=????????????(n>1且n∈N+)型函数的求导,要先化成 y=????????????型,再求导,即y′=????????????′=?????????????????????1).
?
即时巩固
已知f(x)=????32,求f ′(4)以及曲线y=f(x)在点(4,f(4))处的切线的方程.
?
解 因为f ′(x)=32????32?1=32????12,
所以f ′(4)=32×412=32×2=3.
又因为f(4)=432= (22)32?=23=8,
所以所求切线方程为y-8=3(x-4),
即y=3x-4.
?
导数公式表
基本初等函数的导数公式
1.若????(????)=????(????为常数),则?????′(????)=0;
2.若????(????)=????????(????∈????,且????≠0),则?????′(????)=?????????????1;
3.若????(????)=sin?????,则?????′(????)=cos?????;
4.若????(????)=cos?????,则?????′(????)=?sin?????;
5.若????(????)=????????(????>0,且????≠1),则?????′(????)=????????ln?????;
特别地,若????(????)=e????,则?????′(????)=e????;
6.若????(????)=log????????(????>0,且????≠1),则 ;
特别地,若????(????)=ln?????,则?????′(????)=1?????.
基本初等函数的导数公式
对于基本初等函数的导数公式要注意以下三点:
(1)注意y= ?????????(a>0,a≠1)与y= ????????的导数的区别,y= ?????????(a>0,a≠1)与y=log????????(a>0,a≠1)的导数的区别.y′=( ?????????)′= ?????????ln a(a>0,a≠1)与y′=( log?????????)′=1????ln????
(a>0,a≠1)两个公式较难记忆,应加深对公式的理解并强化记忆.
(2)记忆口诀:①指数函数的导数:指导指不变,底对紧相连.
②对数函数的导数:对导是真倒,底对跟着倒.
③正、余弦函数的导数:正余弦互导,余导添负号.
(3)不要求根据导数定义推导这几个函数的导数公式,只要能够利用它们求简单函数的导数即可.
?
即时巩固
已知函数f(x)=ex,g(x)=ln x,求f ′(x),g′(x).
解 在(ax)′=axln a中令a=e,
可得(ex)′=exln e=ex,
因此f ′(x)=ex.
在(logax)′=1????ln?????中令a=e,
可得(logex)′=1????ln?e,
即(ln x)′=1????,
因此g′(x)=1????.
?
典例剖析
例 1 下列结论不正确的是 ( )
A.若y=3,则y′=0 B.若y=1????,则y′=-12????
C.若y=????,则y′=12???? D.若y=x,则y′=1
?
解析 由常数函数的导数为0知A正确;
对于B,y′=1????′=??????12′=-12?????32=?12????3,不正确;
对于C,y′=????′=12?????12=12????,正确;
D正确.
答案 B
?
例 2 求下列函数的导数.
(1)y=????13;(2)y=1????6;(3)y=5????3;(4)y=????13;(5)y=log5x.
?
分析 根据基本初等函数的导数公式求导,对不符合标准形式的适当进行化简.
解 (1)y′=(????13)′=13????12.
(2)y′=1????6′=(x-6)′=-6?????7=?6????7.
(3)y′=(5????3)′=????35′=35?????25=355????2.
(4)y′=????13′=13?????23=133????2.
(5)y′=(log5x)′=1????ln?5.
?
规律总结
(1)用导数的定义求导是求导数的基本方法,但运算较烦琐,利用常用函数的导数公式,可以简化求导过程,降低运算难度.
(2)利用导数公式求导,应根据所给题目的特征,恰当地选择求导公式,有时要将题中函数的结构进行调整,如将根式、分式转化为指数式,再利用幂函数的导数公式求导.
例 3 求函数y=????2+1的导数y′及y′|x=2.
?
解 Δy=????+????????2+1?????2+1=????+????????2+1?????2?1????+????????2+1+????2+1=2????????????+????????2????+????????2+1+????2+1,
则????????????????=2????+????????????+????????2+1+????2+1.
当Δx→0时,lim????????→0????????????????=2????2????2+1=????????2+1,即y′=????????2+1,
所以y′|x=2=222+1=255.
?
类题通法
定义法求导函数的步骤
(1)求Δy=f(x+Δx)-f(x);
(2)求????????????????=????????+?????????????????????????;
(3)计算f ′(x)=lim????????→0????????????????.
上述求导步骤可简记为:一差、二比、三极限.
?
例4 假设某地在20年间的年均通货膨胀率为5%,物价????(单位:元)与时间t(单位:年)
之间的关系为????(????)=????0(1+5%)????,其中????0为????=0时的物价.假定某种商品的 ????0=1,
那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01元/年)?
?
解:根据基本初等函数的导数公式表,有????′(????)=1.05????ln?1.05.
所以????′(10)=1.0510ln?1.05≈0.08.
所以,在第10个年头,这种商品的价格约以0.08元/年的速度上涨.
?
点拨:利用常见函数的导数公式可以解决一些实际问题,如速度增长、变化率等问题,关键是根据题意找出关系式.解题时,认真观察函数的结构特征,积极地进行联想转化,才能抓住问题的本质,把解题思路打开.
例 5 已知曲线y=1????.
(1)求曲线在点P(1,1)处的切线方程;
(2)求曲线过点Q(1,0)的切线方程;
(3)求满足斜率为-13的曲线的切线方程.
?
解 因为y=1????,所以y′=-1????2.
(1)因为P(1,1)是曲线上的点,所以P为切点,
所以切线斜率为k=f ′(1)=-1.
所以曲线在P(1,1)处的切线方程为y-1=-(x-1),即y=-x+2.
(2)显然Q(1,0)不在曲线y=1????上,则可设过该点的切线的切点为A????,1????,
那么该切线斜率为k=f ′(a)=?1????2.
则切线方程为y-1????=?1????2(x-a).①
?
将Q(1,0)代入方程,得0-1????=?1????2(1-a).
解得a=12,
代回方程①整理可得切线方程为y=-4x+4.
(3)设切点为B????,1????,则切线斜率为k=-1????2=?13,
解得b=±3,
所以B3,33,B′?3,?33.
将点B,B '的坐标代入点斜式方程得y-33=?13(x-3),
或y+33=?13(x+3).
整理得切线方程为y=-13x+233或y=-13x-233.
?
类题通法
过不在曲线y=f(x)上一点M(x1,y1)的切线方程的求法
方法1:(1)设切点为P(x0,y0),则y0=f(x0),切线斜率k=f ′(x0).
(2)由kPM=k,得方程k=f ′(x0)=????1?????????0????1?????0.
(3)化简上述方程,得关于x0的方程,可求得x0.
(4)确定y0,k,利用点斜式得切线方程.
方法2:(1)设切点为P(x0,y0),则切线方程为y-y0=k(x-x0).
(2)建立方程组????0=????????0,????=????′????0,????1?????0=????????1?????0.
(3)解方程组,得k,x0,y0,从而得切线方程.
?
随堂小测
1.下列导数式子正确的是 (??)
D
A
B
2.曲线y=????12在点(1,1)处的切线方程为 ( )
A.x-2y+1=0 B.x-y=0 C.x+y-2=0 D.2x-y-1=0
3.设曲线y=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a= ( )
A.-1 B.1 C.-?12 D.?12
4.已知f(x)=x3,则lim????????→0????2+2?????????????2?2????????????????= ( )
A.3 B.12 C.32 D.48
?
D
5.若曲线y=????12在点(a,????12)处的切线与两个坐标轴围成的三角形的面积为22,求a的值.
?
解 y′=12????,????′|????=????=12????,y-????12=12????(x-a).
令x=0,得y=????2,令y=0,得x=-a,
所以围成的三角形的面积为????????4=22,解得a=2.
?
课堂小结
基本初等函数的导数公式
1.若????(????)=????(????为常数),则?????′(????)=0;
2.若????(????)=????????(????∈????,且????≠0),则?????′(????)=?????????????1;
3.若????(????)=sin?????,则?????′(????)=cos?????;
4.若????(????)=cos?????,则?????′(????)=?sin?????;
5.若????(????)=????????(????>0,且????≠1),则?????′(????)=????????ln?????;
特别地,若????(????)=e????,则?????′(????)=e????;
6.若????(????)=log????????(????>0,且????≠1),则 ;
特别地,若????(????)=ln?????,则?????′(????)=1?????.
基本初等函数的导数公式
课堂小结
知识清单:
导函数的定义;公式法求函数的导数;基本初等函数的导数公式.
方法归纳:公式法求函数的导数.
常见误区:基本初等函数的导数公式一定要记牢,这里很容易错用导数公式.
谢 谢!
6.1
导数
6.1.3 基本初等函数的导数
学习目标
1.能用导数的定义求常数函数、幂函数的导数.
2.掌握几个常用函数的导数及其应用.
3.掌握基本初等函数的导数公式及其运用.
4.指数与对数函数的导数公式的区别与运用.
核心素养:数学运算、数学抽象
新知学习
尝试与发现
已知函数f(x)=x2,任取一实数x0,判断f(x)在x0处是否可导.如果可导,求出 f ′(x0),并观察f ′(x0)与x0的关系.
提示:设自变量在x=x0附近的改变量为Δx,则函数在以x0,x0+Δx为端点的闭区间上的平均变化率为 ????????????????=????????0+?????????????????0????????=????0+????????2?????02????????=2x0+Δx.
可以看出,当Δx无限接近于0时,平均变化率无限接近于2????0,因此f(x)在x0处可导,而且
f ′(x0)=lim????????→0????????0+?????????????????0????????=lim????????→0(2x0+Δx)=2x0.
显然,f ′(x0)随x0的变化而变化,而且x0的值确定之后,f ′(x0)也就确定了.
例如,x0=2时,f ′(2)=2×2=4;x0=-3时,f ′(-3)=2×(-3)=-6.
这就说明,f ′(x0)是x0的函数.
?
总结归纳
一般地,如果函数y=f(x)在其定义域内的每一点x都可导,则称f(x)可导.此时,对定义域内的每一个值x,都对应一个确定的导数f ′(x).于是,在f(x)的定义域内,f ′(x)是一个函数,这个函数通常称为函数y=f(x)的导函数,记作f ′(x)(或y′,????′????),即
f ′(x)=y′=????′????=????????????????????→????????????+?????????????????????????.
?
提示:导函数通常也简称为导数.本书后续内容中,除了特别声明指的是求某一点的导数之外,“求导数”均指的是“求导函数”
下面我们看下几个常用函数的导数
1.函数????(????)=????的导数
?
若f?(????)=????(如下图)表示路程关于时间的函数,则f?′(????)=0可以解释为某物体的瞬时速度始终为0,即一直处于静止状态.
?
f ′(x)=lim????????→0????????+?????????????????????????=lim????????→0?????????????????=lim????????→00=0.
?
2.函数????(????)=????的导数
?
若f?(????)=????(如下图)表示路程关于时间的函数,则f?′(????)=1可以解释为某物体做瞬时速度为1的匀速直线运动.
?
f ′(x)=lim????????→0????????+?????????????????????????=lim????????→0????+?????????????????????=lim????????→01=1.
?
3.函数????(????)=????2的导数
?
f?′(????)=2????表示函数f?(????)=????2的图象(如下图)上点(????,????)处切线的斜率为2????,说明随着????的变化,切线的斜率也在变化.另一方面,从导数作为函数在一点的瞬时变化率来看,f?′(????)=2????表明:当????<0时,随着????的增加,|f?′(????)|越来越小,f?(????)=????2减少得越来越慢;当????>0时,随着????的增加,|f?′(????)|越来越大,f?(????)=????2增加得越来越快.若f?(????)=????2表示路程关于时间的函数,则f?′(????)=2????可以解释为某物体做变速运动,它在时刻x的瞬时速度为2????.
?
4.函数????(????)=????3 的导数
?
????′(????)=3????2表示函数????(????)=????3的图象(如下图)上点(????,????)处切线的斜率为3????2,这说明随着????的变化,切线的斜率也在变化,且恒为非负数.
?
f ′(x)=lim????????→0????????+?????????????????????????=lim????????→0????+????????3?????3????????
=lim????????→0[3x2+3xΔx+(Δx)2]=3x2.
?
5.函数????(????)=1?????的导数
?
f ′(x)=lim????????→0????????+?????????????????????????=lim????????→01????+?????????1????????????
?=lim????????→0?1????????+????????=?1????2.
?
探究:画出函数????(????)=1?????的图象.根据图象,描述它的变化情况,并求出曲线在点(1,1)
处的切线方程.
?
函数????(????)=1?????的图象如图所示,
函数????(????)=1????的导数为????′(????)=1????′=?1????2-.
结合函数????(????)=1????的图象可以发现:
当????<0时,函数值????(????)随着????的增加,减少得越来越快;
当????>0时,函数值????(????)随着????的增加,减少得越来越慢.
曲线????(????)=1????在点(1,1)处的切线的斜率就是导函数????′(????)=?1????2在????=1处的函数值,即切线的斜率为?1,
故曲线y= ????(????)在点(1,1)处的切线方程为y=?????+2,
?
6.函数????(????)=???? 的导数
?
说明:前面我们根据导数的定义求出了一些常用函数的导数,这些函数都是幂函数????(????)=????????的形式,在以后求导数时,可直接应用上述常见函数的导数,不必再用定义去求导.
?
总结归纳
(1)对常见幂函数的导数及任意幂函数y=xα的求导都要重点背.
(2)函数y=C,y=x,y=x2,y=x3,y=?????1,y=????12的导数以及幂函数y=xα的求导公式,在以后的求导中可以直接运用,不必再利用导数定义去求,但要理解其推导过程.
(3)对不能直接运用公式的要适当进行变形,如y=1????7=?????7,y=5????2=????25等(即对于y=????????????(n>1且n∈N+)型函数的求导,要先化成 y=????????????型,再求导,即y′=????????????′=?????????????????????1).
?
即时巩固
已知f(x)=????32,求f ′(4)以及曲线y=f(x)在点(4,f(4))处的切线的方程.
?
解 因为f ′(x)=32????32?1=32????12,
所以f ′(4)=32×412=32×2=3.
又因为f(4)=432= (22)32?=23=8,
所以所求切线方程为y-8=3(x-4),
即y=3x-4.
?
导数公式表
基本初等函数的导数公式
1.若????(????)=????(????为常数),则?????′(????)=0;
2.若????(????)=????????(????∈????,且????≠0),则?????′(????)=?????????????1;
3.若????(????)=sin?????,则?????′(????)=cos?????;
4.若????(????)=cos?????,则?????′(????)=?sin?????;
5.若????(????)=????????(????>0,且????≠1),则?????′(????)=????????ln?????;
特别地,若????(????)=e????,则?????′(????)=e????;
6.若????(????)=log????????(????>0,且????≠1),则 ;
特别地,若????(????)=ln?????,则?????′(????)=1?????.
基本初等函数的导数公式
对于基本初等函数的导数公式要注意以下三点:
(1)注意y= ?????????(a>0,a≠1)与y= ????????的导数的区别,y= ?????????(a>0,a≠1)与y=log????????(a>0,a≠1)的导数的区别.y′=( ?????????)′= ?????????ln a(a>0,a≠1)与y′=( log?????????)′=1????ln????
(a>0,a≠1)两个公式较难记忆,应加深对公式的理解并强化记忆.
(2)记忆口诀:①指数函数的导数:指导指不变,底对紧相连.
②对数函数的导数:对导是真倒,底对跟着倒.
③正、余弦函数的导数:正余弦互导,余导添负号.
(3)不要求根据导数定义推导这几个函数的导数公式,只要能够利用它们求简单函数的导数即可.
?
即时巩固
已知函数f(x)=ex,g(x)=ln x,求f ′(x),g′(x).
解 在(ax)′=axln a中令a=e,
可得(ex)′=exln e=ex,
因此f ′(x)=ex.
在(logax)′=1????ln?????中令a=e,
可得(logex)′=1????ln?e,
即(ln x)′=1????,
因此g′(x)=1????.
?
典例剖析
例 1 下列结论不正确的是 ( )
A.若y=3,则y′=0 B.若y=1????,则y′=-12????
C.若y=????,则y′=12???? D.若y=x,则y′=1
?
解析 由常数函数的导数为0知A正确;
对于B,y′=1????′=??????12′=-12?????32=?12????3,不正确;
对于C,y′=????′=12?????12=12????,正确;
D正确.
答案 B
?
例 2 求下列函数的导数.
(1)y=????13;(2)y=1????6;(3)y=5????3;(4)y=????13;(5)y=log5x.
?
分析 根据基本初等函数的导数公式求导,对不符合标准形式的适当进行化简.
解 (1)y′=(????13)′=13????12.
(2)y′=1????6′=(x-6)′=-6?????7=?6????7.
(3)y′=(5????3)′=????35′=35?????25=355????2.
(4)y′=????13′=13?????23=133????2.
(5)y′=(log5x)′=1????ln?5.
?
规律总结
(1)用导数的定义求导是求导数的基本方法,但运算较烦琐,利用常用函数的导数公式,可以简化求导过程,降低运算难度.
(2)利用导数公式求导,应根据所给题目的特征,恰当地选择求导公式,有时要将题中函数的结构进行调整,如将根式、分式转化为指数式,再利用幂函数的导数公式求导.
例 3 求函数y=????2+1的导数y′及y′|x=2.
?
解 Δy=????+????????2+1?????2+1=????+????????2+1?????2?1????+????????2+1+????2+1=2????????????+????????2????+????????2+1+????2+1,
则????????????????=2????+????????????+????????2+1+????2+1.
当Δx→0时,lim????????→0????????????????=2????2????2+1=????????2+1,即y′=????????2+1,
所以y′|x=2=222+1=255.
?
类题通法
定义法求导函数的步骤
(1)求Δy=f(x+Δx)-f(x);
(2)求????????????????=????????+?????????????????????????;
(3)计算f ′(x)=lim????????→0????????????????.
上述求导步骤可简记为:一差、二比、三极限.
?
例4 假设某地在20年间的年均通货膨胀率为5%,物价????(单位:元)与时间t(单位:年)
之间的关系为????(????)=????0(1+5%)????,其中????0为????=0时的物价.假定某种商品的 ????0=1,
那么在第10个年头,这种商品的价格上涨的速度大约是多少(精确到0.01元/年)?
?
解:根据基本初等函数的导数公式表,有????′(????)=1.05????ln?1.05.
所以????′(10)=1.0510ln?1.05≈0.08.
所以,在第10个年头,这种商品的价格约以0.08元/年的速度上涨.
?
点拨:利用常见函数的导数公式可以解决一些实际问题,如速度增长、变化率等问题,关键是根据题意找出关系式.解题时,认真观察函数的结构特征,积极地进行联想转化,才能抓住问题的本质,把解题思路打开.
例 5 已知曲线y=1????.
(1)求曲线在点P(1,1)处的切线方程;
(2)求曲线过点Q(1,0)的切线方程;
(3)求满足斜率为-13的曲线的切线方程.
?
解 因为y=1????,所以y′=-1????2.
(1)因为P(1,1)是曲线上的点,所以P为切点,
所以切线斜率为k=f ′(1)=-1.
所以曲线在P(1,1)处的切线方程为y-1=-(x-1),即y=-x+2.
(2)显然Q(1,0)不在曲线y=1????上,则可设过该点的切线的切点为A????,1????,
那么该切线斜率为k=f ′(a)=?1????2.
则切线方程为y-1????=?1????2(x-a).①
?
将Q(1,0)代入方程,得0-1????=?1????2(1-a).
解得a=12,
代回方程①整理可得切线方程为y=-4x+4.
(3)设切点为B????,1????,则切线斜率为k=-1????2=?13,
解得b=±3,
所以B3,33,B′?3,?33.
将点B,B '的坐标代入点斜式方程得y-33=?13(x-3),
或y+33=?13(x+3).
整理得切线方程为y=-13x+233或y=-13x-233.
?
类题通法
过不在曲线y=f(x)上一点M(x1,y1)的切线方程的求法
方法1:(1)设切点为P(x0,y0),则y0=f(x0),切线斜率k=f ′(x0).
(2)由kPM=k,得方程k=f ′(x0)=????1?????????0????1?????0.
(3)化简上述方程,得关于x0的方程,可求得x0.
(4)确定y0,k,利用点斜式得切线方程.
方法2:(1)设切点为P(x0,y0),则切线方程为y-y0=k(x-x0).
(2)建立方程组????0=????????0,????=????′????0,????1?????0=????????1?????0.
(3)解方程组,得k,x0,y0,从而得切线方程.
?
随堂小测
1.下列导数式子正确的是 (??)
D
A
B
2.曲线y=????12在点(1,1)处的切线方程为 ( )
A.x-2y+1=0 B.x-y=0 C.x+y-2=0 D.2x-y-1=0
3.设曲线y=ax2在点(1,a)处的切线与直线2x-y-6=0平行,则a= ( )
A.-1 B.1 C.-?12 D.?12
4.已知f(x)=x3,则lim????????→0????2+2?????????????2?2????????????????= ( )
A.3 B.12 C.32 D.48
?
D
5.若曲线y=????12在点(a,????12)处的切线与两个坐标轴围成的三角形的面积为22,求a的值.
?
解 y′=12????,????′|????=????=12????,y-????12=12????(x-a).
令x=0,得y=????2,令y=0,得x=-a,
所以围成的三角形的面积为????????4=22,解得a=2.
?
课堂小结
基本初等函数的导数公式
1.若????(????)=????(????为常数),则?????′(????)=0;
2.若????(????)=????????(????∈????,且????≠0),则?????′(????)=?????????????1;
3.若????(????)=sin?????,则?????′(????)=cos?????;
4.若????(????)=cos?????,则?????′(????)=?sin?????;
5.若????(????)=????????(????>0,且????≠1),则?????′(????)=????????ln?????;
特别地,若????(????)=e????,则?????′(????)=e????;
6.若????(????)=log????????(????>0,且????≠1),则 ;
特别地,若????(????)=ln?????,则?????′(????)=1?????.
基本初等函数的导数公式
课堂小结
知识清单:
导函数的定义;公式法求函数的导数;基本初等函数的导数公式.
方法归纳:公式法求函数的导数.
常见误区:基本初等函数的导数公式一定要记牢,这里很容易错用导数公式.
谢 谢!
