高中数学选择性必修第三册RJ·B--6.2 利用导数研究函数的性质-6.2.1 导数与函数的单调性 课件(共32张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·B--6.2 利用导数研究函数的性质-6.2.1 导数与函数的单调性 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览








文档简介
第六章
6.2
利用导数研究函数的性质
6.2.1 导数与函数的单调性
学习目标
1.掌握导数与函数单调性之间的关系,会利用导数研究函数的单调性.
2.会利用导数判断函数的单调性,会求不超过三次的多项式函数的单调区间.
3.掌握求函数单调区间的步骤.
核心素养:数学抽象、数学运算、逻辑推理
新知学习
在必修第一册中,我们通过图象直观,利用不等式、方程等知识,研究了函数的单调性、周期性、奇偶性以及最大(小)值等性质.在本章前两节中,我们学习了导数的概念和运算,知道导数是关于瞬时变化率的数学表达,它定量地刻画了函数的局部变化.能否利用导数更加精确地研究函数的性质呢?本节我们就来讨论这个问题.
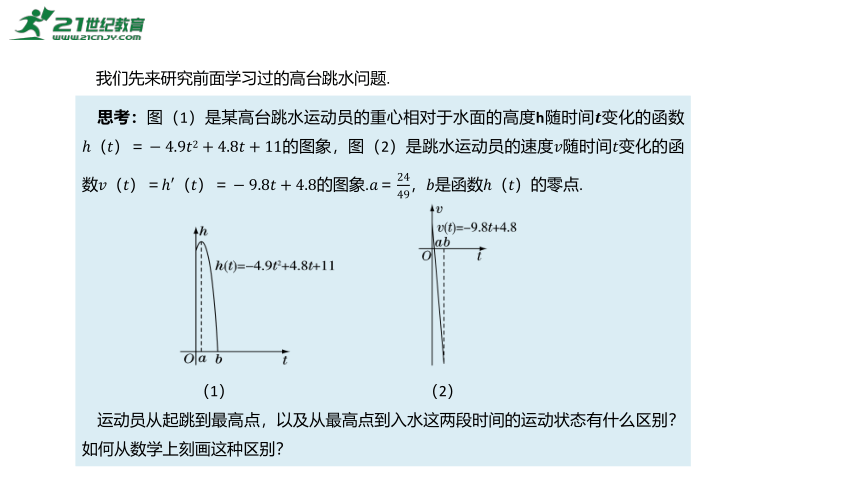
我们先来研究前面学习过的高台跳水问题.
思考:图(1)是某高台跳水运动员的重心相对于水面的高度h随时间????变化的函数?(????)=?4.9????2+4.8????+11的图象,图(2)是跳水运动员的速度????随时间????变化的函数????(????)=?′(????)=?9.8????+4.8的图象.????=2449,????是函数?(????)的零点.
????
?
?
?
??????(1)?????????? ?(2)
运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
?
观察图象可以发现:
(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度?随时间????的增加而增加,即?(????)单调递增.相应地,????(????)=?′(????)>0.
(2)从最高点到入水,运动员的重心处于下降状态,离水面的高度?随时间????的增加而减小,即?(????)单调递减.相应地,????(????)=?′(????)<0.
?
思考:我们看到,函数?(????)的单调性与?′(????)的正负有内在联系.那么,我们能否由?′(????)的正负来判断函数?(????)的单调性呢?
?
对于高台跳水问题,可以发现:
当????∈(0,????)时,?′(????)>0,函数?(????)的图象是“上升”的,函数?(????)在(0,????)上单调递增;
当????∈(????,????)时,?′(????)<0,函数?(????)的图象是“下降”的,函数?(????)在(????,????)上单调递减.
这种情况是否具有一般性呢?
?
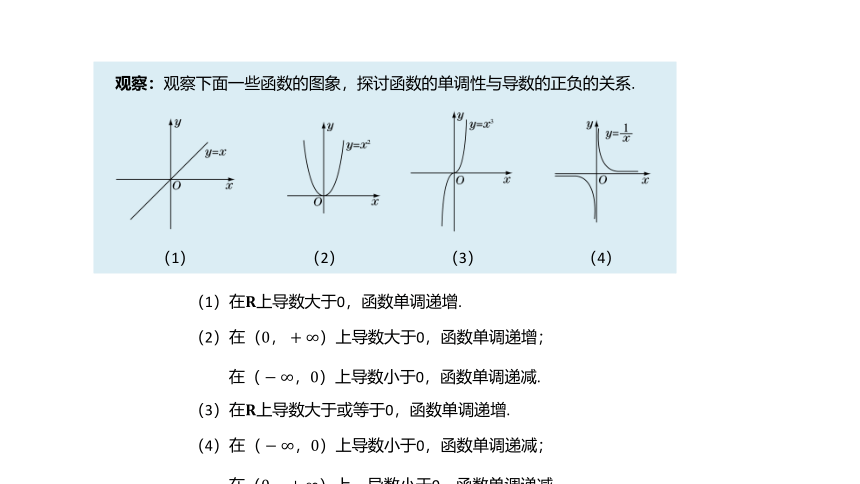
观察:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
(1) (2) (3) (4)
(1)在????上导数大于0,函数单调递增.
(2)在(0,+∞)上导数大于0,函数单调递增;
在(?∞,0)上导数小于0,函数单调递减.
(3)在????上导数大于或等于0,函数单调递增.
(4)在(?∞,0)上导数小于0,函数单调递减;
在(0,+∞)上,导数小于0,函数单调递减.
?
如图,导数?????′(????0)表示函数????=????(????)的图象在点(????0,????(????0))处的切线的斜率.
可以发现:
在????=????0处,?????′(????0)>0,切线是“左下右上”的上升式,
函数????(????)的图象也是上升的,函数????(????)在????=????0附近单调递增;
在????=????1处,?????′(????1)<0,切线是“左上右下”的下降式,
函数????(????)的图象也是下降的,函数????(????)在????=????1附近单调递减.
?
一般地,函数????(????)的单调性与导函数?????′(????)的正负之间具有如下的关系:
在某个区间(????,????)上,如果?????′(????)>0,那么函数????=????(????)在区间(????,????)上单调递增;
在某个区间(????,????)上,如果?????′(????)<0,那么函数????=????(????)在区间(????,????)上单调递减.
?
思考:如果在某个区间上恒有?????′(????)=0,那么函数????(????)有什么特性?
?
如果在某个区间内恒有?????′(????)=0,那么函数????(????)为常数函数;但是在某个区间内,若仅有有限个点所对应的导数值为0,则不能判定????(????)为常数函数.
?
提示:(1)在某个区间内,?????′(????)>0(?????′(????)<0)是函数????(????)在此区间内单调递增(减)的充分条件,而不是必要条件.例如,函数????(????)=????3在定义域(?∞,+∞)上单调递增,但?????′(????)=3????2≥0.
(2)函数????(????)在(????,????)内单调递增(减)的充要条件是?????′(????)≥0(?????′(????)≤0)在(????,????)内恒成立,且?????′(????)在(????,????)的任意子区间内都不恒等于0.这就是说,在区间的个别点处有?????′(????)=0并不影响函数????(????)在该区间的单调性.
?
即时巩固
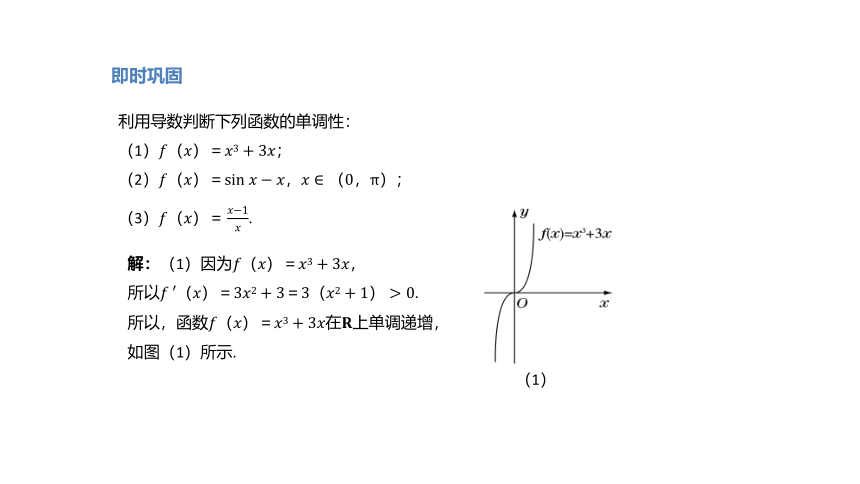
利用导数判断下列函数的单调性:
(1)????(????)=????3+3????;
(2)????(????)=sin??????????,????∈(0,π);
(3)????(????)=?????1????.
?
解:(1)因为????(????)=????3+3????,
所以?????′(????)=3????2+3=3(????2+1)>0.
所以,函数????(????)=????3+3????在????上单调递增,
如图(1)所示.
?
(1)
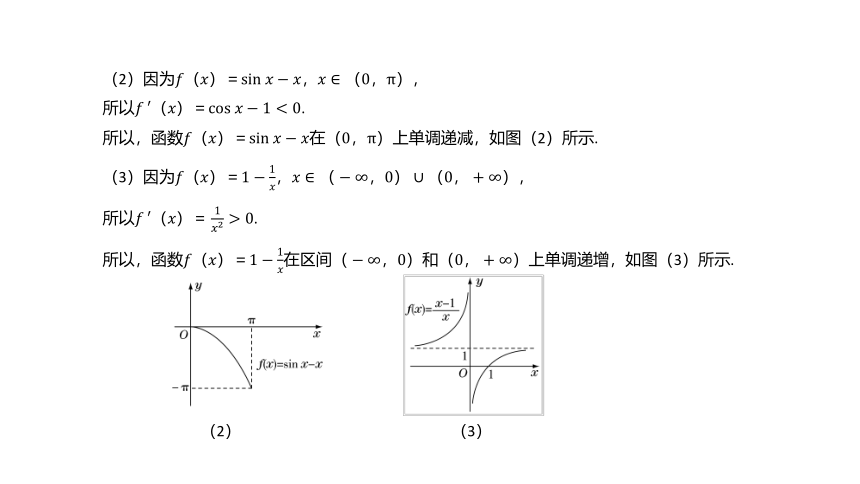
(2)因为????(????)=sin??????????,????∈(0,π),
所以?????′(????)=cos??????1<0.
所以,函数????(????)=sin??????????在(0,π)上单调递减,如图(2)所示.
(3)因为????(????)=1?1????,????∈(?∞,0)∪(0,+∞),
所以?????′(????)=1????2>0.
所以,函数????(????)=1?1????在区间(?∞,0)和(0,+∞)上单调递增,如图(3)所示.
?
(2) (3)
一般地,
(1)如果在区间(a,b)内,f ′(x)>0,则曲线y=f(x)在区间(a,b)对应的那一段上每一点处切线的斜率都大于0,曲线呈上升状态,因此f(x)在(a,b)上是增函数,如图所示;
(2)如果在区间(a,b)内,f ′(x)<0,则曲线y=f(x)在区间(a,b)对应的那一段上每一点处切线的斜率都小于0,曲线呈下降状态,因此f(x)在(a,b)上是减函数,如图所示.
请同学们回顾一下函数单调性的定义,并思考在某个区间上单调的函数????=????(????)的平均变化率的几何意义与?????′(????)的正负的关系.
?
在区间(????,????)内,任取????(????1,????(????1)),????(????2,????(????2))两点,则函数????(????)的平均变化率 ,其几何意义为直线????????的斜率.
?
利用上述性质,我们可以求出函数的单调区间.
知识应用:我们试画出如下条件的函数????(????)图象的大致形状.
已知导函数?????′(????)的下列信息:
当10;当????<1,或????>4时,?????′(????)<0;
当????=1,或????=4时,?????′(????)=0.
?
解:当10,可知????(????)在区间(1,4)上单调递增;
当????<1,或????>4时,?????′(????)<0,可知????(????)在区间(?∞,1)和(4,+∞)上都单调递减;
当????=1,或????=4时,?????′(????)=0,这两点比较特殊,我们称它们为“临界点”.
综上,函数????(????)图象的大致形状如图所示.
?
问题:求函数????(????)=13????3?12????2?2????+1的单调区间.
解:函数????(????)=13????3?12????2?2????+1的定义域为????.
对????(????)求导数,得
?????′(????)=????2??????2=(????+1)(?????2).
令?????′(????)=0,解得????=?1,或????=2.
????=?1和????=2把函数定义域划分成三个区间,?????′(????)在各区间上的正负,以及????(????)的单调性如下表所示.
?
问题研究:形如????(????)=????????3+????????2+????????+????(????≠0)的函数应用广泛,下面我们利用导数来研究这类函数的单调性.
?
???
???
???
????
(?∞,?1)
?1
(?1,2)
2
(2,+∞)
?????′(????)
+
0
?
0
+
????(????)
单调递增
????(?1)=136
单调递减
????(2)=?73
单调递增
单调递增
单调递减
单调递增
所以,????(????)在(?∞,?1)和(2,+∞)上单调递增,在(?1,2)上单调递减,
如图所示.
?
如果不用导数的方法,直接运用单调性的定义,你如何求解本题?运算过程麻烦吗?你有什么体会?
运用单调性的定义求解本题时,应先在定义域内任取????1,????2(????1?
总结
求函数的单调区间,就是解不等式f ′(x)>0或f ′(x)<0,不等式的解集就是所求的单调区间,求解步骤如下:
(1)求函数f(x)的定义域;
(2)求出f ′(x);
(3)解不等式f ′(x)>0可得函数f(x)的单调递增区间,解不等式f ′(x)<0可得函数f(x)的单调递减区间.
探究:研究对数函数????=ln?????与幂函数????=????3在区间(0,+∞)上增长快慢的情况.
?
??????
对数函数????=ln?????的导数为????′=1????>0(????∈(0,+∞)),所以????=ln?????在区间(0,+∞)上单调递增.当????越来越大时,????′=1?????越来越小,所以函数????=ln?????递增得越来越慢,图象上升得越来越“平缓”(如图(1)).
幂函数????=????3的导数为????′=3????2>0(????∈(0,+∞)),所以????=????3在区间(0,+∞)上单调递增.当????越来越大时,????′=3????2越来越大,函数????=????3递增得越来越快,图象上升得越来越“陡峭”(如图(2)).
?
(1)?????????????(2)
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
总结:函数的变化快慢与导数的关系
即时巩固
设????>0,????(????)=ln?????,????(????)=1?1????,两个函数的图象如图所示.
判断????(????),????(????)的图象与????1,????2 之间的对应关系.
?
解:因为????(????)=ln?????,????(????)=1?1????,
所以?????′(????)=1????,????′(????)=1????2.
当????=1时,?????′(????)=????′(????)=1;
当0?????′(????)>1;
当????>1时,0 所以,????(????),????(????)在(0,+∞)上都是增函数.
在区间(0,1)上,????(????)的图象比????(????)的图象要
“陡峭”;在区间(1,+∞)上,????(????)的图象比????(????)
的图象要“平缓”.
所以,????(????),????(????)的图象依次是图中的????2,????1.
?
典例剖析
例1 已知函数f(x)的图像如图所示,下列四个图像中f ′(x)
(其中f ′(x)是函数f(x)的导函数)的图像大致是( )
A B C D
解析:由题中函数图像可知,函数在(-∞,0)上先单调递减再单调递增,最后单调递减,在(0,+∞)上单调递增,则其导函数在(-∞,0)上,由左往右先小于零,再大于零,最后小于零,故排除A,B;在(0,+∞)上大于零,故排除C,故选D.
答案:D
方法技巧
函数图像的辨识可以从以下几个方面入手
(1)从函数的定义域,判断图像在左右位置;从函数的值域,判断图像的上下位置.
(2)从函数的单调性,判断图像的变化趋势.
(3)从函数的奇偶性,判断图像的对称性.
(4)从函数的特殊点入手,排除不符合要求的图像.总之,利用上述方法排除、筛选选项.
规律总结
原函数与导函数图像问题的解读
(1)函数图像的单调性可以通过导数的正负来分析判断,即符号为正,图像上升,符号为负,图像下降,看导函数图像时,主要是看图像在x轴上方还是下方,即关心导数的正负,而不是其单调性.解决问题时,一定要分清是函数图像还是导函数图像.
(2)记忆口诀:“原函数看增减,导函数看正负”.
例2 求下列函数的单调区间.
(1)y=x3-12x2-2x+5;(2)f(x)=ex+e-x;(3)y=????2????+x(k>0);(4)y=2x2-ln x.
?
解题提示 观察分析各函数的结构特点,确定函数定义域,求导,再求单调区间.
解(1)y′=3x2-x-2=(3x+2)(x-1).当x∈?∞,?23∪(1,+∞)时,y′>0,当x∈?23,1时,y′<0,
∴ 函数y的单调递增区间为?∞,?23,(1,+∞),单调递减区间为?23,1.
(2)f ′(x)=ex-e-x=e2?????1e????,令f ′(x)>0,得x>0,令f ′(x)<0,得x<0,
∴ f(x)的单调递增区间为(0,+∞),单调递减区间为(-∞,0).
(3)y′=1-????2????2,当x∈(-∞,-k)∪(k,+∞)时,y′>0;当x∈(-k,0)∪(0,k)时,y′<0,
∴ 函数y的单调递增区间为(-∞,-k),(k,+∞),单调递减区间为(-k,0),(0,k).
(4)y′=4x-1????=4????2?1????,函数的定义域为(0,+∞).当x∈0,12时,y′<0;当x∈12,+∞时,y′>0,
∴ 函数y的单调递增区间为12,+∞,单调递减区间为0,12.
?
类题通法
利用导数求函数的单调区间的方法
求可导函数f(x)的单调区间一般有两种方法:一种是解不等式法;另一种是列表法.
(1)用解不等式法求单调区间的步骤:
①确定函数f(x)的定义域;②求导函数f ′(x);③解不等式f ′(x)>0(或f ′(x)<0),
并写出解集;④根据③的结果确定函数f(x)的单调区间.
(2)用列表法求单调区间的步骤:
①确定函数f(x)的定义域;②求导函数f ′(x);③解方程f ′(x)=0;④列表;⑤得出结论.
例3 设g(x)=ln x-ax2+(a-2)x,a<0,试讨论函数g(x)的单调性.
解题提示 先对原函数求导得g′(x)=-????????+12?????1????(x>0),再对a分类讨论得函数 g(x)的单调性.
解 由题意可知g′(x)=1????-2ax+a-2=-????????+12?????1????(x>0).∵ a<0,g′(x)=-????????+1????2?????1????(x>0),
(1)当a<-2时,∵ -1????<12,∴ g′(x)=-????????+1????2?????1????>0等价于????+1????(2x-1)>0,
易得函数g(x)在0,?1????和12,+∞上单调递增,同理可得在?1????,12上单调递减;
(2)当a=-2时,g′(x)=2?????12????≥0恒成立,∴ 函数g(x)在(0,+∞)上单调递增;
(3)当-212,∴ g′(x)=-????????+1????2?????1????>0等价于????+1????(2x- 1)>0,
易得函数g(x)在0,12和?1????,+∞上单调递增,同理可得在12,?1????上单调递减.
?
类题通法
利用导数研究含参函数f(x)的单调区间的一般步骤
(1)确定函数f(x)的定义域;
(2)求导数f ′(x);
(3)分析参数对区间端点、最高次项的系数的影响,以及不等式解集的端点与定义域的关系,恰当确定参数的不同范围,并进行分类讨论;
(4)在不同的参数范围内,解不等式f ′(x)>0和f ′(x)<0,确定函数f(x)的单调区间.
例4 若函数h(x)=ln x-12ax2-2x(a≠0)在[1,4]上单调递减,求实数a的取值范围.
?
解题提示 分析原函数的定义域,对原函数求导,然后根据h(x)在[1,4]上单调递减,得到h′(x)≤0恒成立,从而可分离参数a,求其范围.
解 因为h(x)=ln x-12ax2-2x,x∈(0,+∞),所以h′(x)=1????-ax-2.
因为h(x)在[1,4]上单调递减,所以当x∈[1,4]时,h′(x)=1????-ax-2≤0恒成立,即a≥1????2-2????恒成立,
令G(x)=1????2-2????,x∈[1,4],则a≥G(x)最大值,而G(x)=1?????12-1.
因为x∈[1,4],所以1????∈14,1,所以G(x)最大值=-716(此时x=4),所以a≥-716.
当a=-716时,h′(x)=1????+716x-2=16+7????2?32????16????=7?????4?????416????.
因为x∈[1,4],所以h′(x)=7?????4?????416????≤0,即h(x)在[1,4]上为减函数.
故实数a的取值范围是?716,+∞.
?
类题通法
已知函数的单调性求参数取值范围的解题思路
(1)可导函数在区间(a,b)上单调,实际上就是在该区间上f ′(x)≥0(或f ′(x)≤0)恒成立,得到关于参数的不等式,从而转化为求函数的最值问题,求出参数的取值范围,注意检验等号成立时导数是否在(a,b)上恒为0.
(2)如函数在某个区间上恒增或恒减问题,导函数不方便分离参数,且为二次函数时,可以借助二次函数的性质对问题进行研究.方法一:直接分类讨论函数的最值;方法二:可以借助函数的图像研究.
?
随堂小测
1.已知?????′(????)是????(????)的导函数,?????′(????)的图象如图所示,
则????(????)的图象只可能是(? )
?
A B C D
D
2.函数????=????3?2????2+????+1的单调递增区间为 ( )
?
A. B. C. D.
C
3.已知函数????(????)=?????????1????+1?ln?????在[1,+∞)上是减函数,则实数????的取值范围为(? )
A.????<1 B. ????≤2 C.?????<2 D. ????≤3
?
B
4.证明:函数????(????)=2????2?ln?????在区间12,+∞上单调递增,在区间0,12上单调递减.
?
证明:函数的定义域为(0,+∞).?????′(????)=4?????1????=
当????∈12,+∞时,2????+1>0,2?????1>0,????>0,∴?????′????>0,
∴?????(????)在12,+∞上单调递增.
当????∈0,12时,2????+1>0,2?????1<0,????>0,∴?????′????<0,
∴?????(????)在0,12上单调递减.
?
5.证明不等式sin x?
证明:(1)先证x∈0,π2时,sin x设f(x)=sin x-x,x∈0,π2,f ′(x)=cos x-1<0,所以f(x)在0,π2上单调递减.
又f(0)=sin 0-0=0,故x∈0,π2时,f(x)(2)再证x∈0,π2时, x设g(x)=x-tan x,显然g(x)在0,π2上有定义.
因为g ′(x)=1-1cos2????,由x∈0,π2,知1cos2????>1,g ′(x)<0,
所以g(x)在0,π2上单调递减.
又g(0)=0,故x∈0,π2时,g(x)综上所述,当x∈0,π2时,有sin x?
课堂小结
知识清单:
单调性与导函数;利用导数研究函数图象与单调性的关系;利用导数判断函数的单调性;利用导数求函数的单调区间
方法归纳: 利用函数的导数大小判断函数单调性,图像法判断函数的单调性
常见误区:求函数单调区间时,容易忽略函数的定义域.
谢 谢!
6.2
利用导数研究函数的性质
6.2.1 导数与函数的单调性
学习目标
1.掌握导数与函数单调性之间的关系,会利用导数研究函数的单调性.
2.会利用导数判断函数的单调性,会求不超过三次的多项式函数的单调区间.
3.掌握求函数单调区间的步骤.
核心素养:数学抽象、数学运算、逻辑推理
新知学习
在必修第一册中,我们通过图象直观,利用不等式、方程等知识,研究了函数的单调性、周期性、奇偶性以及最大(小)值等性质.在本章前两节中,我们学习了导数的概念和运算,知道导数是关于瞬时变化率的数学表达,它定量地刻画了函数的局部变化.能否利用导数更加精确地研究函数的性质呢?本节我们就来讨论这个问题.
我们先来研究前面学习过的高台跳水问题.
思考:图(1)是某高台跳水运动员的重心相对于水面的高度h随时间????变化的函数?(????)=?4.9????2+4.8????+11的图象,图(2)是跳水运动员的速度????随时间????变化的函数????(????)=?′(????)=?9.8????+4.8的图象.????=2449,????是函数?(????)的零点.
????
?
?
?
??????(1)?????????? ?(2)
运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?如何从数学上刻画这种区别?
?
观察图象可以发现:
(1)从起跳到最高点,运动员的重心处于上升状态,离水面的高度?随时间????的增加而增加,即?(????)单调递增.相应地,????(????)=?′(????)>0.
(2)从最高点到入水,运动员的重心处于下降状态,离水面的高度?随时间????的增加而减小,即?(????)单调递减.相应地,????(????)=?′(????)<0.
?
思考:我们看到,函数?(????)的单调性与?′(????)的正负有内在联系.那么,我们能否由?′(????)的正负来判断函数?(????)的单调性呢?
?
对于高台跳水问题,可以发现:
当????∈(0,????)时,?′(????)>0,函数?(????)的图象是“上升”的,函数?(????)在(0,????)上单调递增;
当????∈(????,????)时,?′(????)<0,函数?(????)的图象是“下降”的,函数?(????)在(????,????)上单调递减.
这种情况是否具有一般性呢?
?
观察:观察下面一些函数的图象,探讨函数的单调性与导数的正负的关系.
(1) (2) (3) (4)
(1)在????上导数大于0,函数单调递增.
(2)在(0,+∞)上导数大于0,函数单调递增;
在(?∞,0)上导数小于0,函数单调递减.
(3)在????上导数大于或等于0,函数单调递增.
(4)在(?∞,0)上导数小于0,函数单调递减;
在(0,+∞)上,导数小于0,函数单调递减.
?
如图,导数?????′(????0)表示函数????=????(????)的图象在点(????0,????(????0))处的切线的斜率.
可以发现:
在????=????0处,?????′(????0)>0,切线是“左下右上”的上升式,
函数????(????)的图象也是上升的,函数????(????)在????=????0附近单调递增;
在????=????1处,?????′(????1)<0,切线是“左上右下”的下降式,
函数????(????)的图象也是下降的,函数????(????)在????=????1附近单调递减.
?
一般地,函数????(????)的单调性与导函数?????′(????)的正负之间具有如下的关系:
在某个区间(????,????)上,如果?????′(????)>0,那么函数????=????(????)在区间(????,????)上单调递增;
在某个区间(????,????)上,如果?????′(????)<0,那么函数????=????(????)在区间(????,????)上单调递减.
?
思考:如果在某个区间上恒有?????′(????)=0,那么函数????(????)有什么特性?
?
如果在某个区间内恒有?????′(????)=0,那么函数????(????)为常数函数;但是在某个区间内,若仅有有限个点所对应的导数值为0,则不能判定????(????)为常数函数.
?
提示:(1)在某个区间内,?????′(????)>0(?????′(????)<0)是函数????(????)在此区间内单调递增(减)的充分条件,而不是必要条件.例如,函数????(????)=????3在定义域(?∞,+∞)上单调递增,但?????′(????)=3????2≥0.
(2)函数????(????)在(????,????)内单调递增(减)的充要条件是?????′(????)≥0(?????′(????)≤0)在(????,????)内恒成立,且?????′(????)在(????,????)的任意子区间内都不恒等于0.这就是说,在区间的个别点处有?????′(????)=0并不影响函数????(????)在该区间的单调性.
?
即时巩固
利用导数判断下列函数的单调性:
(1)????(????)=????3+3????;
(2)????(????)=sin??????????,????∈(0,π);
(3)????(????)=?????1????.
?
解:(1)因为????(????)=????3+3????,
所以?????′(????)=3????2+3=3(????2+1)>0.
所以,函数????(????)=????3+3????在????上单调递增,
如图(1)所示.
?
(1)
(2)因为????(????)=sin??????????,????∈(0,π),
所以?????′(????)=cos??????1<0.
所以,函数????(????)=sin??????????在(0,π)上单调递减,如图(2)所示.
(3)因为????(????)=1?1????,????∈(?∞,0)∪(0,+∞),
所以?????′(????)=1????2>0.
所以,函数????(????)=1?1????在区间(?∞,0)和(0,+∞)上单调递增,如图(3)所示.
?
(2) (3)
一般地,
(1)如果在区间(a,b)内,f ′(x)>0,则曲线y=f(x)在区间(a,b)对应的那一段上每一点处切线的斜率都大于0,曲线呈上升状态,因此f(x)在(a,b)上是增函数,如图所示;
(2)如果在区间(a,b)内,f ′(x)<0,则曲线y=f(x)在区间(a,b)对应的那一段上每一点处切线的斜率都小于0,曲线呈下降状态,因此f(x)在(a,b)上是减函数,如图所示.
请同学们回顾一下函数单调性的定义,并思考在某个区间上单调的函数????=????(????)的平均变化率的几何意义与?????′(????)的正负的关系.
?
在区间(????,????)内,任取????(????1,????(????1)),????(????2,????(????2))两点,则函数????(????)的平均变化率 ,其几何意义为直线????????的斜率.
?
利用上述性质,我们可以求出函数的单调区间.
知识应用:我们试画出如下条件的函数????(????)图象的大致形状.
已知导函数?????′(????)的下列信息:
当10;当????<1,或????>4时,?????′(????)<0;
当????=1,或????=4时,?????′(????)=0.
?
解:当10,可知????(????)在区间(1,4)上单调递增;
当????<1,或????>4时,?????′(????)<0,可知????(????)在区间(?∞,1)和(4,+∞)上都单调递减;
当????=1,或????=4时,?????′(????)=0,这两点比较特殊,我们称它们为“临界点”.
综上,函数????(????)图象的大致形状如图所示.
?
问题:求函数????(????)=13????3?12????2?2????+1的单调区间.
解:函数????(????)=13????3?12????2?2????+1的定义域为????.
对????(????)求导数,得
?????′(????)=????2??????2=(????+1)(?????2).
令?????′(????)=0,解得????=?1,或????=2.
????=?1和????=2把函数定义域划分成三个区间,?????′(????)在各区间上的正负,以及????(????)的单调性如下表所示.
?
问题研究:形如????(????)=????????3+????????2+????????+????(????≠0)的函数应用广泛,下面我们利用导数来研究这类函数的单调性.
?
???
???
???
????
(?∞,?1)
?1
(?1,2)
2
(2,+∞)
?????′(????)
+
0
?
0
+
????(????)
单调递增
????(?1)=136
单调递减
????(2)=?73
单调递增
单调递增
单调递减
单调递增
所以,????(????)在(?∞,?1)和(2,+∞)上单调递增,在(?1,2)上单调递减,
如图所示.
?
如果不用导数的方法,直接运用单调性的定义,你如何求解本题?运算过程麻烦吗?你有什么体会?
运用单调性的定义求解本题时,应先在定义域内任取????1,????2(????1?
总结
求函数的单调区间,就是解不等式f ′(x)>0或f ′(x)<0,不等式的解集就是所求的单调区间,求解步骤如下:
(1)求函数f(x)的定义域;
(2)求出f ′(x);
(3)解不等式f ′(x)>0可得函数f(x)的单调递增区间,解不等式f ′(x)<0可得函数f(x)的单调递减区间.
探究:研究对数函数????=ln?????与幂函数????=????3在区间(0,+∞)上增长快慢的情况.
?
??????
对数函数????=ln?????的导数为????′=1????>0(????∈(0,+∞)),所以????=ln?????在区间(0,+∞)上单调递增.当????越来越大时,????′=1?????越来越小,所以函数????=ln?????递增得越来越慢,图象上升得越来越“平缓”(如图(1)).
幂函数????=????3的导数为????′=3????2>0(????∈(0,+∞)),所以????=????3在区间(0,+∞)上单调递增.当????越来越大时,????′=3????2越来越大,函数????=????3递增得越来越快,图象上升得越来越“陡峭”(如图(2)).
?
(1)?????????????(2)
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.
总结:函数的变化快慢与导数的关系
即时巩固
设????>0,????(????)=ln?????,????(????)=1?1????,两个函数的图象如图所示.
判断????(????),????(????)的图象与????1,????2 之间的对应关系.
?
解:因为????(????)=ln?????,????(????)=1?1????,
所以?????′(????)=1????,????′(????)=1????2.
当????=1时,?????′(????)=????′(????)=1;
当0?????′(????)>1;
当????>1时,0 所以,????(????),????(????)在(0,+∞)上都是增函数.
在区间(0,1)上,????(????)的图象比????(????)的图象要
“陡峭”;在区间(1,+∞)上,????(????)的图象比????(????)
的图象要“平缓”.
所以,????(????),????(????)的图象依次是图中的????2,????1.
?
典例剖析
例1 已知函数f(x)的图像如图所示,下列四个图像中f ′(x)
(其中f ′(x)是函数f(x)的导函数)的图像大致是( )
A B C D
解析:由题中函数图像可知,函数在(-∞,0)上先单调递减再单调递增,最后单调递减,在(0,+∞)上单调递增,则其导函数在(-∞,0)上,由左往右先小于零,再大于零,最后小于零,故排除A,B;在(0,+∞)上大于零,故排除C,故选D.
答案:D
方法技巧
函数图像的辨识可以从以下几个方面入手
(1)从函数的定义域,判断图像在左右位置;从函数的值域,判断图像的上下位置.
(2)从函数的单调性,判断图像的变化趋势.
(3)从函数的奇偶性,判断图像的对称性.
(4)从函数的特殊点入手,排除不符合要求的图像.总之,利用上述方法排除、筛选选项.
规律总结
原函数与导函数图像问题的解读
(1)函数图像的单调性可以通过导数的正负来分析判断,即符号为正,图像上升,符号为负,图像下降,看导函数图像时,主要是看图像在x轴上方还是下方,即关心导数的正负,而不是其单调性.解决问题时,一定要分清是函数图像还是导函数图像.
(2)记忆口诀:“原函数看增减,导函数看正负”.
例2 求下列函数的单调区间.
(1)y=x3-12x2-2x+5;(2)f(x)=ex+e-x;(3)y=????2????+x(k>0);(4)y=2x2-ln x.
?
解题提示 观察分析各函数的结构特点,确定函数定义域,求导,再求单调区间.
解(1)y′=3x2-x-2=(3x+2)(x-1).当x∈?∞,?23∪(1,+∞)时,y′>0,当x∈?23,1时,y′<0,
∴ 函数y的单调递增区间为?∞,?23,(1,+∞),单调递减区间为?23,1.
(2)f ′(x)=ex-e-x=e2?????1e????,令f ′(x)>0,得x>0,令f ′(x)<0,得x<0,
∴ f(x)的单调递增区间为(0,+∞),单调递减区间为(-∞,0).
(3)y′=1-????2????2,当x∈(-∞,-k)∪(k,+∞)时,y′>0;当x∈(-k,0)∪(0,k)时,y′<0,
∴ 函数y的单调递增区间为(-∞,-k),(k,+∞),单调递减区间为(-k,0),(0,k).
(4)y′=4x-1????=4????2?1????,函数的定义域为(0,+∞).当x∈0,12时,y′<0;当x∈12,+∞时,y′>0,
∴ 函数y的单调递增区间为12,+∞,单调递减区间为0,12.
?
类题通法
利用导数求函数的单调区间的方法
求可导函数f(x)的单调区间一般有两种方法:一种是解不等式法;另一种是列表法.
(1)用解不等式法求单调区间的步骤:
①确定函数f(x)的定义域;②求导函数f ′(x);③解不等式f ′(x)>0(或f ′(x)<0),
并写出解集;④根据③的结果确定函数f(x)的单调区间.
(2)用列表法求单调区间的步骤:
①确定函数f(x)的定义域;②求导函数f ′(x);③解方程f ′(x)=0;④列表;⑤得出结论.
例3 设g(x)=ln x-ax2+(a-2)x,a<0,试讨论函数g(x)的单调性.
解题提示 先对原函数求导得g′(x)=-????????+12?????1????(x>0),再对a分类讨论得函数 g(x)的单调性.
解 由题意可知g′(x)=1????-2ax+a-2=-????????+12?????1????(x>0).∵ a<0,g′(x)=-????????+1????2?????1????(x>0),
(1)当a<-2时,∵ -1????<12,∴ g′(x)=-????????+1????2?????1????>0等价于????+1????(2x-1)>0,
易得函数g(x)在0,?1????和12,+∞上单调递增,同理可得在?1????,12上单调递减;
(2)当a=-2时,g′(x)=2?????12????≥0恒成立,∴ 函数g(x)在(0,+∞)上单调递增;
(3)当-2
易得函数g(x)在0,12和?1????,+∞上单调递增,同理可得在12,?1????上单调递减.
?
类题通法
利用导数研究含参函数f(x)的单调区间的一般步骤
(1)确定函数f(x)的定义域;
(2)求导数f ′(x);
(3)分析参数对区间端点、最高次项的系数的影响,以及不等式解集的端点与定义域的关系,恰当确定参数的不同范围,并进行分类讨论;
(4)在不同的参数范围内,解不等式f ′(x)>0和f ′(x)<0,确定函数f(x)的单调区间.
例4 若函数h(x)=ln x-12ax2-2x(a≠0)在[1,4]上单调递减,求实数a的取值范围.
?
解题提示 分析原函数的定义域,对原函数求导,然后根据h(x)在[1,4]上单调递减,得到h′(x)≤0恒成立,从而可分离参数a,求其范围.
解 因为h(x)=ln x-12ax2-2x,x∈(0,+∞),所以h′(x)=1????-ax-2.
因为h(x)在[1,4]上单调递减,所以当x∈[1,4]时,h′(x)=1????-ax-2≤0恒成立,即a≥1????2-2????恒成立,
令G(x)=1????2-2????,x∈[1,4],则a≥G(x)最大值,而G(x)=1?????12-1.
因为x∈[1,4],所以1????∈14,1,所以G(x)最大值=-716(此时x=4),所以a≥-716.
当a=-716时,h′(x)=1????+716x-2=16+7????2?32????16????=7?????4?????416????.
因为x∈[1,4],所以h′(x)=7?????4?????416????≤0,即h(x)在[1,4]上为减函数.
故实数a的取值范围是?716,+∞.
?
类题通法
已知函数的单调性求参数取值范围的解题思路
(1)可导函数在区间(a,b)上单调,实际上就是在该区间上f ′(x)≥0(或f ′(x)≤0)恒成立,得到关于参数的不等式,从而转化为求函数的最值问题,求出参数的取值范围,注意检验等号成立时导数是否在(a,b)上恒为0.
(2)如函数在某个区间上恒增或恒减问题,导函数不方便分离参数,且为二次函数时,可以借助二次函数的性质对问题进行研究.方法一:直接分类讨论函数的最值;方法二:可以借助函数的图像研究.
?
随堂小测
1.已知?????′(????)是????(????)的导函数,?????′(????)的图象如图所示,
则????(????)的图象只可能是(? )
?
A B C D
D
2.函数????=????3?2????2+????+1的单调递增区间为 ( )
?
A. B. C. D.
C
3.已知函数????(????)=?????????1????+1?ln?????在[1,+∞)上是减函数,则实数????的取值范围为(? )
A.????<1 B. ????≤2 C.?????<2 D. ????≤3
?
B
4.证明:函数????(????)=2????2?ln?????在区间12,+∞上单调递增,在区间0,12上单调递减.
?
证明:函数的定义域为(0,+∞).?????′(????)=4?????1????=
当????∈12,+∞时,2????+1>0,2?????1>0,????>0,∴?????′????>0,
∴?????(????)在12,+∞上单调递增.
当????∈0,12时,2????+1>0,2?????1<0,????>0,∴?????′????<0,
∴?????(????)在0,12上单调递减.
?
5.证明不等式sin x
证明:(1)先证x∈0,π2时,sin x
又f(0)=sin 0-0=0,故x∈0,π2时,f(x)
因为g ′(x)=1-1cos2????,由x∈0,π2,知1cos2????>1,g ′(x)<0,
所以g(x)在0,π2上单调递减.
又g(0)=0,故x∈0,π2时,g(x)
课堂小结
知识清单:
单调性与导函数;利用导数研究函数图象与单调性的关系;利用导数判断函数的单调性;利用导数求函数的单调区间
方法归纳: 利用函数的导数大小判断函数单调性,图像法判断函数的单调性
常见误区:求函数单调区间时,容易忽略函数的定义域.
谢 谢!
