高中数学选择性必修第三册RJ·B--6.2 利用导数研究函数的性质-6.2.2 导数与函数的极值、最值 课件(共39张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册RJ·B--6.2 利用导数研究函数的性质-6.2.2 导数与函数的极值、最值 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 09:18:46 | ||
图片预览






文档简介
第六章
6.2
利用导数研究函数的性质
6.2.2 导数与函数的极值、最值
学习目标
1.了解函数的极大(小)值、最大(小)值的概念.
2.了解函数的极值与最值的区别和联系.
3.掌握求函数的极值与最值的方法.
核心素养:逻辑推理、数学运算
新知学习
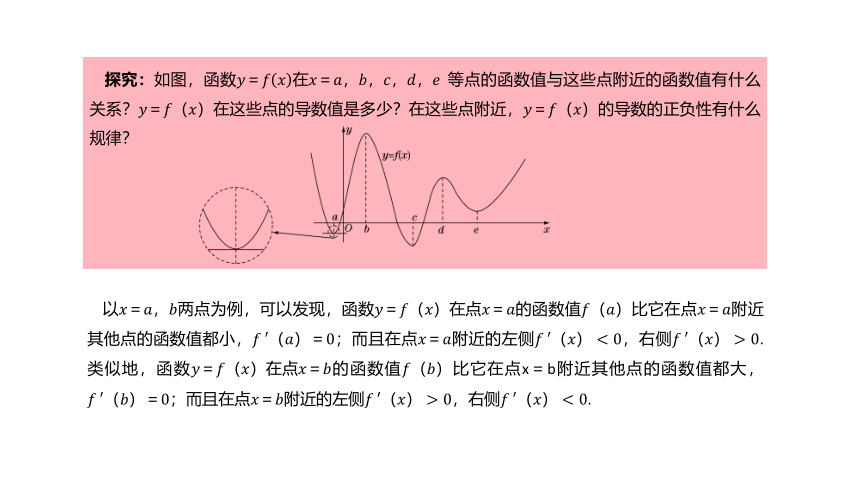
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的增减.如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
观察下图,我们发现,当????=????时,高台跳水运动员距水面的高度最大.那么,函数?(????)在此点的导数是多少呢?此点附近的图象有什么特点?相应地,导数的正负性有什么变化规律?
?
放大????=????附近函数?(????)的图象,如上图.可以看出,?′(????)=0;在????=????的附近,当????0;当????>????时,函数?(????)单调递减,?′(????)<0.这就是说,在????=????附近,函数值先增(当????0)后减(当????>????时,?′(????)<0).这样,当????在????的附近从小到大经过????时,?′(????)先正后负,且?′(????)连续变化,于是有?′(????)=0.
?
思考:对于一般的函数????=????(????),是否也有上边同样的性质呢?
?
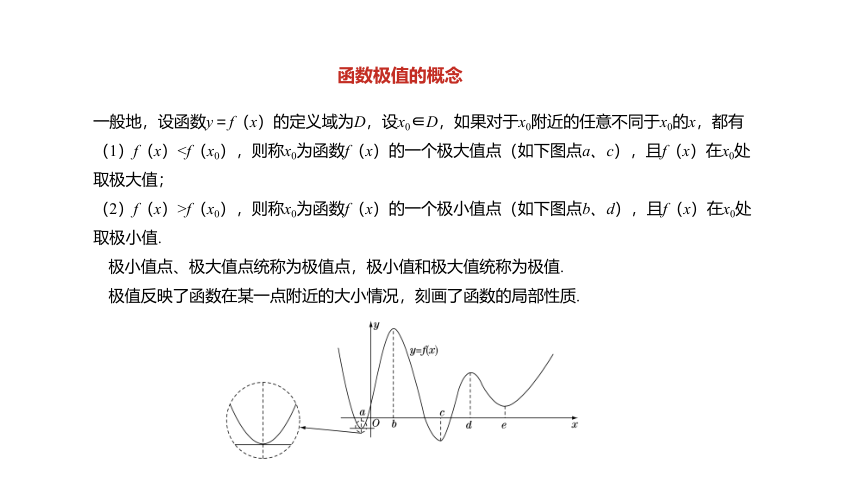
探究:如图,函数????=????????在????=????,????,????,????,??????等点的函数值与这些点附近的函数值有什么关系?????=????(????)在这些点的导数值是多少?在这些点附近,????=????(????)的导数的正负性有什么规律?
?
以????=????,????两点为例,可以发现,函数????=????(????)在点????=????的函数值????(????)比它在点????=????附近其他点的函数值都小,?????′(????)=0;而且在点????=????附近的左侧?????′(????)<0,右侧?????′(????)>0.类似地,函数????=????(????)在点????=????的函数值????(????)比它在点x=b附近其他点的函数值都大,?????′(????)=0;而且在点????=????附近的左侧?????′(????)>0,右侧?????′(????)<0.
?
一般地,设函数y=f(x)的定义域为D,设x0∈D,如果对于x0附近的任意不同于x0的x,都有
(1)f(x)(2)f(x)>f(x0),则称x0为函数f(x)的一个极小值点(如下图点b、d),且f(x)在x0处取极小值.
极小值点、极大值点统称为极值点,极小值和极大值统称为极值.
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
函数极值的概念
思考:导数值为0的点一定是函数的极值点吗?
导数值为0的点不一定是函数的极值点.例如,对于函数????(????)=????3,我们有?????′(????)=3????2.虽然?????′(0)=0,但由于无论????>0,还是????<0,恒有?????′(????)>0,即函数????(????)=????3是增函数,所以0不是函数????(????)=????3的极值点.
一般地,函数????=????(????)在一点的导数值为0是函数????=????(????)在这点取极值的必要条件,而非充分条件.
?
总结概括:一般地,设函数f(x)在x0处可导,且f ′(x0)=0.
(1)如果对于x0左侧附近的任意x,都有f ′(x)>0,对于x0右侧附近的任意x,都有f ′(x)<0,那么此时x0是f(x)的极大值点.
(2)如果对于x0左侧附近的任意x,都有f ′(x)<0,对于x0右侧附近的任意x,都有f ′(x)>0,那么此时x0是f(x)的极小值点.
(3)如果f ′(x)在x0的左侧附近与右侧附近均为正号(或均为负号),则x0一定不是y= f(x)的极值点.
概念阐释
(1)极值是一个局部性概念.由极值的定义知,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个定义域内最大或最小,即反映的是函数在某一点附近的情况.
(2)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点.
(3)函数的极值不一定是唯一的,即一个函数在某个区间上或定义域内的极大值或极小值可以不止一个.
(4)如果函数f(x)在[a,b]上有极值,那么它的极值点的分布是有规律的.一般地,当函数f(x)在[a,b]上的图像连续且有有限个极值点时,函数f(x)在[a,b]内的极大值点、极小值点是交替出现的.
即时巩固
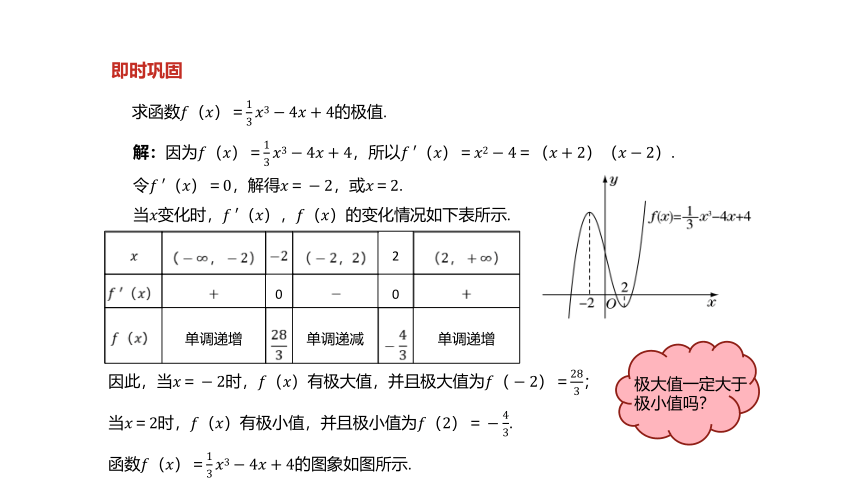
求函数????(????)=13????3?4????+4的极值.
?
解:因为????(????)=13????3?4????+4,所以?????′(????)=????2?4=(????+2)(?????2).
令?????′(????)=0,解得????=?2,或????=2.
当????变化时,?????′(????),????(????)的变化情况如下表所示.
?
????
(?∞,?2)
?2
(?2,2)
2
(2,+∞)
?????′(????)
+
0
?
0
+
????(????)
单调递增
283
单调递减
?43
单调递增
2
0
0
单调递增
单调递减
单调递增
因此,当????=?2时,????(????)有极大值,并且极大值为????(?2)=283;
当????=2时,????(????)有极小值,并且极小值为????(2)=?43.
函数????(????)=13????3?4????+4的图象如图所示.
?
极大值一定大于极小值吗?
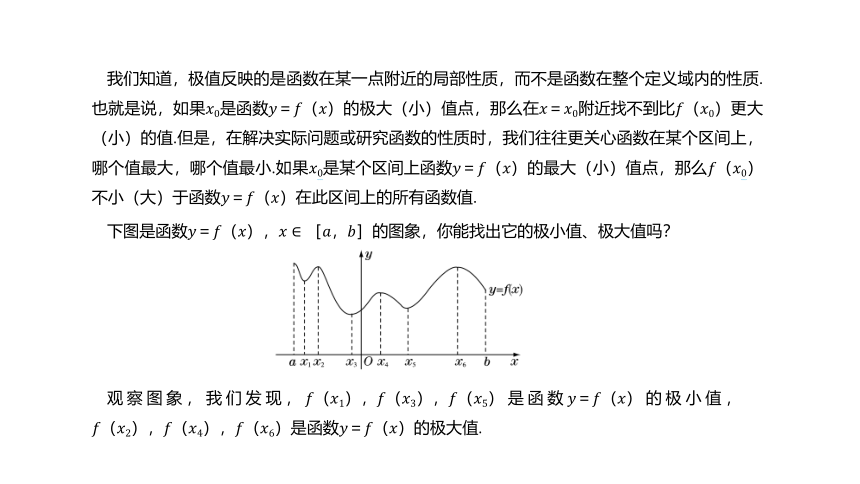
我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质.也就是说,如果????0是函数????=????(????)的极大(小)值点,那么在????=????0附近找不到比????(????0)更大(小)的值.但是,在解决实际问题或研究函数的性质时,我们往往更关心函数在某个区间上,哪个值最大,哪个值最小.如果????0是某个区间上函数????=????(????)的最大(小)值点,那么????(????0)不小(大)于函数????=????(????)在此区间上的所有函数值.
?
下图是函数????=????(????),????∈[????,????]的图象,你能找出它的极小值、极大值吗?
?
观察图象,我们发现,????(????1),????(????3),????(????5)是函数????=????(????)的极小值,????(????2),????(????4),????(????6)是函数????=????(????)的极大值.
?
探究:进一步地,你能找出函数????=????(????)在区间[????,????]上的最小值、最大值吗?
?
从图中可以看出,函数????=????(????)在区间[????,????]上的最小值是????(????3),最大值是????(????).
?
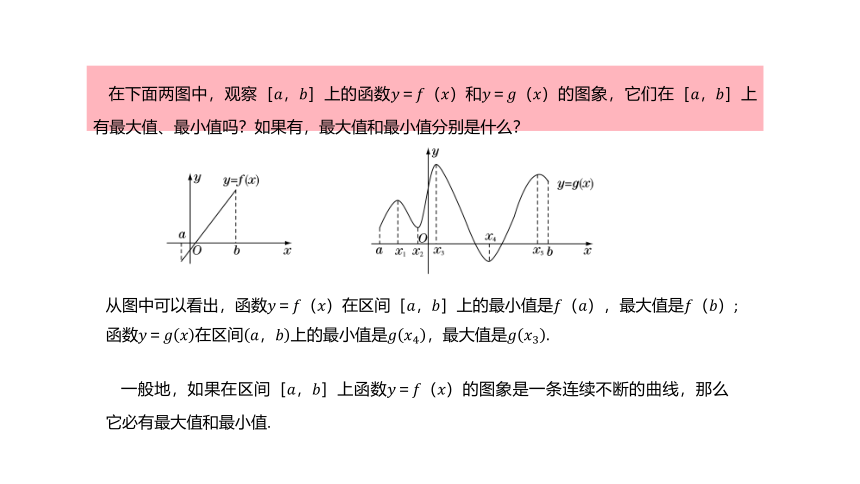
在下面两图中,观察[????,????]上的函数????=????(????)和????=????(????)的图象,它们在[????,????]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
?
?????
从图中可以看出,函数????=????(????)在区间[????,????]上的最小值是????(????),最大值是????(????);
函数????=????????在区间????,????上的最小值是????????4,最大值是????????3.
?
一般地,如果在区间[????,????]上函数????=????(????)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
?
总结概括:一般地,如果函数y=f(x)在定义域内的每一点都可导,且函数存在最值,则函数的最值点一定是某个极值点;如果函数y=f(x)的定义域为[a,b]且存在最值,函数y=f(x)在(a,b)内可导,那么函数的最值点要么是区间端点a或b,要么是极值点.
在开区间(????,????)上函数的最值常见的有以下几种情况:
图(1)中的函数????=????(????)在(????,????)上有最大值而无最小值;
图(2)中的函数????=????(????)在(????,????)上有最小值而无最大值;
图(3)中的函数????=????(????)在(????,????)上既无最大值又无最小值;
图(4)中的函数????=????(????)在(????,????)上既有最大值又有最小值;
?
?
(1) (2) (3) (4)
概念阐释
函数y=f(x),x∈[a,b],如果对任意x∈[a,b],存在x0∈[a,b]有f(x)≤f(x0)(或f(x)≥
f(x0)),则称f(x0)为函数f(x)的最大值(或最小值),其中x0为f(x)的最大值点(或最小值点).
提示
(1)如果f(x)在闭区间[a,b]上的图像是一条连续不断的曲线,则f(x)在[a,b]上必存在最大值和最小值.
(2)函数的最值是一个整体概念,它是函数在区间内所有函数值中的最大者(或最小者).
(3)函数的最值在闭区间的极值点或端点处取得.
(4)若函数f(x)在闭区间[a,b]上是单调函数,则可直接利用单调性法求函数的最值,即若f(x)在[a,b]上递增,则f(x)的最大值为f(b),最小值为f(a);若f(x)在[a,b]上递减,则f(x)的最大值为f(a),最小值为f(b).
例如,函数f(x)=x3在[-1,3]上为增函数,则f(x)在[-1,3]上的最小值为f(-1)=-1,最大值为f(3)=27.
求函数????(????)=13????3?4????+4在区间[0,3]上的最大值与最小值.
?
解:由已知可知,在区间[0,3]上,当????=2时,函数????(????)=13????3?4????+4有极小值,并且极小值为????(2)=?43.
又由于????(0)=4,????(3)=1,
所以,函数????(????)=13????3?4????+4在区间[0,3]上的最大值是4,最小值是?43.
上述结论可以从函数????(????)=13????3?4????+4在区间[0,3]上的图象得到直观验证.
?
即时巩固
典例剖析
例1已知函数y=f(x)的导函数f ′(x)的图像如图所示,则下列判断正确的是( )
A.函数y=f(x)在区间?3,?12内单调递增
B.当x=-2时,函数y=f(x)取得极小值
C.函数y=f(x)在区间(-2,2)内单调递增
D.当x=3时,函数y=f(x)有极小值
?
解析 对于A,函数y=f(x)在区间?3,?12内有增有减,故A不正确;对于B,当x=-2时,函数y=f(x)取得极小值,故B正确;对于C,当x∈(-2,2)时,恒有f ′(x)>0,则函数y=f(x)在区间(-2,2)上单调递增,故C正确;对于D,当x=3时,f ′(x)≠0,故D不正确.
答案 BC
?
例2 设f(x)=ax3+bx+c为奇函数,且其图像在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f ′(x)的最小值为-12.
(1)求a,b,c的值.
(2)求函数f(x)在[-2,3]上的极大值和极小值.
解题提示 (1)先根据奇函数求出c的值,再根据导函数f ′(x)的最小值求出b的值,最后依据在x=1处的导数等于切线的斜率求出a的值即可;
(2)先求导数f ′(x),在函数的定义域内解不等式f ′(x)>0和f ′(x)<0,求得区间即为单调区间,进而得到函数的极值.
解 (1)∵ f(x)为奇函数,∴ f(-x)=-f(x),即-ax3-bx+c=-ax3-bx-c,∴ c=0.
∵ f ′(x)=3ax2+b的最小值为-12,∴ b=-12.
又直线x-6y-7=0的斜率为16,
∴ f ′(1)=3a+b=-6,∴ a=2,b=-12,c=0.
(2)f(x)=2x3-12x,f ′(x)=6(x+2)(x-2),
令f ′(x)=0得x=-2或x=2,
当x变化时,f ′(x),f(x)的变化情况如下表:
∴ 函数f(x)的单调增区间是[-2,-2)和(2,3],函数f(x)的单调递减区间是(-2,2),
∴ f(x)在[-2,3]上的极大值是f(-2)=82,极小值是f(2)=-82.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
[-2,-2)
-2
(-2,2)
2
(2,3]
f ′(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
f ′(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
规律总结
求函数f(x)极值的步骤
(1)确定函数的定义域;
(2)求导数f ′(x);
(3)解方程f ′(x)=0,求出函数在定义域内的所有根;
(4)列表观察f ′(x)在f ′(x)=0的根x0左右两侧值的符号,如果左正右负(左增右减),那么f(x)在x0处取极大值,如果左负右正(左减右增),那么f(x)在x0处取极小值;
(5)如果只有一个极值点,则在该处既是极值也是最值.
例3 若函数f(x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,则实数a的取值范围为( )
A.-12
解题提示 先求导函数,根据函数f (x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,可得f ′(x)=3x2+6ax+3(a+2)=0有两个不等的实数根,从而可以求得实数a的取值范围.
解析 ∵ f(x)=x3+3ax2+3(a+2)x+1,∴ f ′(x)=3x2+6ax+3(a+2).
∵ 函数f(x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,
∴ f ′(x) =3x2+6ax+3(a+2)=0有两个不等的实数根,
∴ 36a2-36(a+2)>0,即a2-a-2>0,
解得a<-1或a>2,
答案 D
规律总结
逆向应用函数的极值,主要是含参数的问题,应注意两个方面:
一是注意对参数的分类讨论,要抓住讨论的切入点;
二是一般要对结果进行检验,以验证充分必要性.
例4 已知函数f(x)=x-2????-3ln x+1.
(1)求函数f(x)的单调区间;
(2)求f(x)在区间[1,e2]上的值域.
?
解题提示
(1)函数f(x)的定义域是(0,+∞),f '(x)=1+2????2-3????=????2?3????+2????2=?????1?????2????2,
可得当x变化时,f '(x),f(x)的变化情况,进而得出函数f(x)的单调区间;
(2)由(1)可知在区间(1,e2)内,当x=2时,f(x)取得极小值,可得
f(2)?
解 (1)函数f(x)的定义域是(0,+∞),
f '(x)=1+2????2-3????=????2?3????+2????2=?????1?????2????2.
当x变化时,f '(x),f(x)的变化情况如下表:
所以f(x)在(0,1)和(2,+∞)上单调递增,在(1,2)上单调递减.
(2)由(1)可知在区间(1,e2)内,当x=2时,f(x)取得极小值 ,
f(1)=0,f(2)=2-3ln 2,f(e2)=e2-2e2-5,
得f(2)所以f(x)在区间[1,e2]上的值域为2?3ln?2,e2?2e2?5.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(0,1)
1
(1,2)
2
(2,+∞)
f '(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
类题通法
求函数f(x)最值的基本步骤
(1)求导函数:求函数f(x)的导函数f ′(x).
(2)求极值可疑点:即求出f ′(x)不存在的点或f ′(x)=0的点.
(3)列表:依极值可疑点将函数的定义域分成若干个子区间,列出f ′(x)与f(x)随x变化的一览表.
(4)求极值:依(3)的表中所反映的相关信息,求出f(x)的极值点和极值.
(5)求区间端点函数值.
(6)求最值:比较极值可疑点和区间端点的函数值后,得出函数f(x)在其定义域内的最大值和最小值.
一般地,最大(小)值是由区间端点的函数值和极大(小)(包括导数不存在的点)值比较而得.
例5 已知函数f(x)=ex-3x+3a(e为自然对数的底数,a∈R).
(1)求f(x)的单调区间与极值;
(2)求证:当a>ln3e,且x>0时,e???????? >32x-3a+1????.
?
解题提示
(1)先求出f ′(x)>0,f ′(x)<0分别可得递增区间和递减区间,代值计算,可得结果.
(2)通过构造函数g(x)=ex-32x2+3ax-1,利用导数结合(1)的结论,可知g(x)在(0,+∞)上单调递增,然后根据g(x)>g(0),可得结果.
?
(1)解:由f(x)=ex-3x+3a,知f ′(x)=ex-3.
令f ′(x)=0,得x=ln 3,
于是当x变化时,f ′(x),f(x)的变化情况如下表:
故f(x)的单调递减区间是(-∞,ln 3],单调递增区间是[ln 3,+∞),
f(x)在x=ln 3处取得极小值,极小值为f (ln 3)=eln 3-3ln 3+3a=3-3ln 3+3a. 无极大值.
(2)证明:待证不等式等价于ex>32x2-3ax+1,
设g(x)=ex-32x2+3ax-1,x>0,于是g′(x)=ex-3x+3a,x>0.
由(1)及a>ln3e=ln 3-1知:g′(x)的最小值为g′(ln 3)=3(1-ln 3+a)>0.
于是对任意x>0,都有g′(x)>0,所以g(x)在(0,+∞)内单调递增.
于是当a>ln3e=ln 3-1时,对任意x∈(0,+∞),都有g(x)>g(0).
而g(0)=0,从而对任意x∈(0,+∞),g(x)>0. 即ex>32x2-3ax+1,故e????????>32x-3a+1????.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(-∞,ln 3)
ln 3
(ln 3,+∞)
f ′(x)
-
0
+
f(x)
?
极小值
?
类题通法
构造函数法证明不等式中常见的方法
(1)移项法:证明不等式f(x)>g(x)(f(x)f(x)-g(x)>0(f(x)-g(x)<0),进而构造辅助函数h(x)=f(x)-g(x).
(2)构造“形似”函数:对原不等式同解变形,如移项、通分、取对数;把不等式转化为左右两边是相同结构的式子的结构,根据“相同结构”构造辅助函数.
(3)放缩法:若所构造函数最值不易求解,可将所证明的不等式进行放缩,再重新构造函数.
例6 已知函数f (x)=xex-????12????2+????(a∈R).
(1)当a=0时,求函数f(x)的极值;
(2)若?x∈(-2,0),f(x)≤0恒成立,求实数a的取值范围.
?
解 (1)当a=0时,f ′(x)=(x+1)ex,当x<-1时f ′(x)<0;当x>-1时f ′(x)>0,
∴ f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增.
∴ f(x)的极小值为f(-1)=-1e,无极大值.
(2)∵ 对?x∈(-2,0),f(x)≤0恒成立,∴ a≤2e????????+2在(-2,0)上恒成立.
令g(x)=2e????????+2(-2当-20,
∴ g(x)在(-2,-1)上单调递减,在(-1,0)上单调递增,
∴ g(x)min=g(-1)=2e?1?1+2=2e,∴ 实数a的取值范围为?∞,2e.
?
类题通法
不等式恒(能)成立的求解策略
“恒成立”与“存在性”问题的求解是“互补”关系,即f(x)≥g(x)对于x∈D恒成立,应求f(x)的最小值;若存在x∈D,使得f(x)≥g(x)成立,应求f(x)的最大值.在具体问题中究竟是求最大值还是最小值,可以先联想“恒成立”是求最大值还是最小值,这样就可以解决相应的“存在性”问题是求最大值还是最小值,特别需要关注等号是否成立问题,以免细节出错.
例7 设函数f(x)=????22-kln x,k>0.
(1)求f(x)的单调区间和极值;
(2)证明:若f(x)存在零点,则f(x)在区间(1,e]上仅有一个零点.
?
解题提示
(1)对函数f(x)求导,根据导数的正负确定函数的单调区间和极值;
(2)根据(1)中函数的单调性和极值分析函数图像,得出最值,进而得出函数存在零点时k的取值范围,由此结合零点存在性定理进行证明.
(1)解:由f(x)=????22-kln x(k>0,x>0)得f ′(x)=x-????????=????2?????????,由f ′(x)=0,解得x=????.
当x变化时,f ′(x)与f(x)在区间(0,+∞)上的变化情况如下表:
所以f(x)的单调递减区间是(0,????),单调递增区间是(????,+∞),x=????处取得极小值f(????)=????1?ln?????2.
(2)证明:由(1)知,f(x)在区间(0,+∞)上的最小值为f(????)=????1?ln?????2.
因为f(x)存在零点,所以????1?ln?????2≤0,从而k≥e.
当k=e时,f(x)在区间(1,e)上单调递减,且f(e)=0,所以x=e是f(x)在区间(1,e]上的唯一零点.
当k>e时,f(x)在区间(1,e)上单调递减,且f(1)=12>0,f(e)=e?????2<0,
所以f(x)在区间(1,e]上仅有一个零点.
综上可知,若f(x)存在零点,则f(x)在区间(1,e]上仅有一个零点.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(0,????)
????
(????,+∞)
f ′(x)
-
0
+
f(x)
?
????1?ln?????2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
f ′(x)
-
0
+
f(x)
?
?
类题通法
利用导数研究零点的个数
函数的零点个数也就是函数图像与x轴交点的个数,所以可利用数形结合的方法判断交点个数,如果函数较为复杂,可结合导数知识确定极值点和单调区间从而确定其函数的大致图像.对于含参函数的零点个数,一般可从两个方面讨论:一是利用导数研究函数的单调性和极值,作出函数的大致图像,根据极大值和极小值的符号确定函数零点的个数;二是分离参数,将问题转化为求y=a和y=f(x)的图像的交点个数问题求解.
随堂小测
1.函数????(????)的导函数????=?????′(????)的图象如图所示, 其中?3,2,4是?????′(????)=0的根, 现给出下列命题:
①????(4)是????(????)的极小值;
②????(2)是????(????)的极大值;
③????(?2)是????(????)的极大值;
④????(3)是????(????)的极小值;
⑤????(?3)是????(????)的极大值.
其中正确的命题是 .(填上正确命题的序号)
?
①②
2.若函数????(????)=????3+????????2+????????+????2在????=1处取得极值10,则????= ,????= .
?
4
?11
?
3.若函数????(????)=????3+3????????2+3[(????+2)????+1]既有极大值又有极小值,则????的取值范围是 .
?
(?∞,?1)∪(2,+∞)
?
4.已知函数????(????)=?????2?????3ln?????+1.
(1)求函数????(????)的单调区间;
(2)求????(????)在区间[1,????2]上的值域.
?
(1)单调递增区间为(0,1),(2,+∞),单调递减区间为(1,2).
?
(2)????(????)在区间[1,e2]上的值域为
?
5.设a>0且a为常数,求函数y=e-x-e-2x在区间[0,a]上的最大值和最小值.
解:y′=-e-x+2e-2x=-e-2x(ex-2).
令y′=0,得x=ln 2.
因为x∈[0,a],所以只需研究x≥0的情况,如下表:
又y=e-x-e-2x=e-2x(ex-1),当x>0时,ex-1>0,所以此时y>0.
由上可知:若0ln 2,则在区间[0,a]上,当x=ln 2时,函数有最大值14,当x=0时,函数有最小值0.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
(0,ln 2)
ln 2
(ln 2,+∞)
y′
?
+
0
-
y
0
?
14
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
(0,ln 2)
ln 2
(ln 2,+∞)
y′
?
+
0
-
y
0
?
?
6.设函数f(x)=x3+4x2+4x+c.若函数f(x)有三个不同零点,求c的取值范围.
解:由题意知,f ′(x)=3x2+8x+4.
令f ′(x)=0,得3x2+8x+4=0,解得x=-2或x=-23.
当x变化时,f ′(x)与f(x)的变化情况如下表:
所以,当c>0且c-3227<0,即0所以当c∈0,3227时,函数f(x)=x3+4x2+4x+c有三个不同零点.
?
课堂小结
1.求函数????=????(????)的极值的方法:
解方程?????′(????)=0,当?????′(????0)=0时:
(1)如果在????0附近的左侧?????′(????)>0,右侧?????′(????)<0,那么????(????0)是极大值;
(2)如果在????0附近的左侧?????′(????)<0,右侧?????′(????)>0,那么????(????0)是极小值.
?
2.求函数????=????(????)在区间[????,????]上的最大值与最小值的步骤:
(1)求函数????=????(????)在区间(????,????)上的极值;
(2)将函数????=????(????)的各极值与端点处的函数值????(????),????(????)比较,其中最大的一个是最大值,最小的一个是最小值.
?
课堂小结
知识清单:
函数的极值;利用单数研究函数的最值;
方法归纳:函数最值的求法:求导数-求可能极值点-列表-求极值-求区间端点的函数值-求最值.
常见误区:对函数极值与最值的关系理解不透
谢 谢!
6.2
利用导数研究函数的性质
6.2.2 导数与函数的极值、最值
学习目标
1.了解函数的极大(小)值、最大(小)值的概念.
2.了解函数的极值与最值的区别和联系.
3.掌握求函数的极值与最值的方法.
核心素养:逻辑推理、数学运算
新知学习
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的增减.如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
观察下图,我们发现,当????=????时,高台跳水运动员距水面的高度最大.那么,函数?(????)在此点的导数是多少呢?此点附近的图象有什么特点?相应地,导数的正负性有什么变化规律?
?
放大????=????附近函数?(????)的图象,如上图.可以看出,?′(????)=0;在????=????的附近,当????0;当????>????时,函数?(????)单调递减,?′(????)<0.这就是说,在????=????附近,函数值先增(当????0)后减(当????>????时,?′(????)<0).这样,当????在????的附近从小到大经过????时,?′(????)先正后负,且?′(????)连续变化,于是有?′(????)=0.
?
思考:对于一般的函数????=????(????),是否也有上边同样的性质呢?
?
探究:如图,函数????=????????在????=????,????,????,????,??????等点的函数值与这些点附近的函数值有什么关系?????=????(????)在这些点的导数值是多少?在这些点附近,????=????(????)的导数的正负性有什么规律?
?
以????=????,????两点为例,可以发现,函数????=????(????)在点????=????的函数值????(????)比它在点????=????附近其他点的函数值都小,?????′(????)=0;而且在点????=????附近的左侧?????′(????)<0,右侧?????′(????)>0.类似地,函数????=????(????)在点????=????的函数值????(????)比它在点x=b附近其他点的函数值都大,?????′(????)=0;而且在点????=????附近的左侧?????′(????)>0,右侧?????′(????)<0.
?
一般地,设函数y=f(x)的定义域为D,设x0∈D,如果对于x0附近的任意不同于x0的x,都有
(1)f(x)
极小值点、极大值点统称为极值点,极小值和极大值统称为极值.
极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
函数极值的概念
思考:导数值为0的点一定是函数的极值点吗?
导数值为0的点不一定是函数的极值点.例如,对于函数????(????)=????3,我们有?????′(????)=3????2.虽然?????′(0)=0,但由于无论????>0,还是????<0,恒有?????′(????)>0,即函数????(????)=????3是增函数,所以0不是函数????(????)=????3的极值点.
一般地,函数????=????(????)在一点的导数值为0是函数????=????(????)在这点取极值的必要条件,而非充分条件.
?
总结概括:一般地,设函数f(x)在x0处可导,且f ′(x0)=0.
(1)如果对于x0左侧附近的任意x,都有f ′(x)>0,对于x0右侧附近的任意x,都有f ′(x)<0,那么此时x0是f(x)的极大值点.
(2)如果对于x0左侧附近的任意x,都有f ′(x)<0,对于x0右侧附近的任意x,都有f ′(x)>0,那么此时x0是f(x)的极小值点.
(3)如果f ′(x)在x0的左侧附近与右侧附近均为正号(或均为负号),则x0一定不是y= f(x)的极值点.
概念阐释
(1)极值是一个局部性概念.由极值的定义知,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个定义域内最大或最小,即反映的是函数在某一点附近的情况.
(2)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点.
(3)函数的极值不一定是唯一的,即一个函数在某个区间上或定义域内的极大值或极小值可以不止一个.
(4)如果函数f(x)在[a,b]上有极值,那么它的极值点的分布是有规律的.一般地,当函数f(x)在[a,b]上的图像连续且有有限个极值点时,函数f(x)在[a,b]内的极大值点、极小值点是交替出现的.
即时巩固
求函数????(????)=13????3?4????+4的极值.
?
解:因为????(????)=13????3?4????+4,所以?????′(????)=????2?4=(????+2)(?????2).
令?????′(????)=0,解得????=?2,或????=2.
当????变化时,?????′(????),????(????)的变化情况如下表所示.
?
????
(?∞,?2)
?2
(?2,2)
2
(2,+∞)
?????′(????)
+
0
?
0
+
????(????)
单调递增
283
单调递减
?43
单调递增
2
0
0
单调递增
单调递减
单调递增
因此,当????=?2时,????(????)有极大值,并且极大值为????(?2)=283;
当????=2时,????(????)有极小值,并且极小值为????(2)=?43.
函数????(????)=13????3?4????+4的图象如图所示.
?
极大值一定大于极小值吗?
我们知道,极值反映的是函数在某一点附近的局部性质,而不是函数在整个定义域内的性质.也就是说,如果????0是函数????=????(????)的极大(小)值点,那么在????=????0附近找不到比????(????0)更大(小)的值.但是,在解决实际问题或研究函数的性质时,我们往往更关心函数在某个区间上,哪个值最大,哪个值最小.如果????0是某个区间上函数????=????(????)的最大(小)值点,那么????(????0)不小(大)于函数????=????(????)在此区间上的所有函数值.
?
下图是函数????=????(????),????∈[????,????]的图象,你能找出它的极小值、极大值吗?
?
观察图象,我们发现,????(????1),????(????3),????(????5)是函数????=????(????)的极小值,????(????2),????(????4),????(????6)是函数????=????(????)的极大值.
?
探究:进一步地,你能找出函数????=????(????)在区间[????,????]上的最小值、最大值吗?
?
从图中可以看出,函数????=????(????)在区间[????,????]上的最小值是????(????3),最大值是????(????).
?
在下面两图中,观察[????,????]上的函数????=????(????)和????=????(????)的图象,它们在[????,????]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
?
?????
从图中可以看出,函数????=????(????)在区间[????,????]上的最小值是????(????),最大值是????(????);
函数????=????????在区间????,????上的最小值是????????4,最大值是????????3.
?
一般地,如果在区间[????,????]上函数????=????(????)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
?
总结概括:一般地,如果函数y=f(x)在定义域内的每一点都可导,且函数存在最值,则函数的最值点一定是某个极值点;如果函数y=f(x)的定义域为[a,b]且存在最值,函数y=f(x)在(a,b)内可导,那么函数的最值点要么是区间端点a或b,要么是极值点.
在开区间(????,????)上函数的最值常见的有以下几种情况:
图(1)中的函数????=????(????)在(????,????)上有最大值而无最小值;
图(2)中的函数????=????(????)在(????,????)上有最小值而无最大值;
图(3)中的函数????=????(????)在(????,????)上既无最大值又无最小值;
图(4)中的函数????=????(????)在(????,????)上既有最大值又有最小值;
?
?
(1) (2) (3) (4)
概念阐释
函数y=f(x),x∈[a,b],如果对任意x∈[a,b],存在x0∈[a,b]有f(x)≤f(x0)(或f(x)≥
f(x0)),则称f(x0)为函数f(x)的最大值(或最小值),其中x0为f(x)的最大值点(或最小值点).
提示
(1)如果f(x)在闭区间[a,b]上的图像是一条连续不断的曲线,则f(x)在[a,b]上必存在最大值和最小值.
(2)函数的最值是一个整体概念,它是函数在区间内所有函数值中的最大者(或最小者).
(3)函数的最值在闭区间的极值点或端点处取得.
(4)若函数f(x)在闭区间[a,b]上是单调函数,则可直接利用单调性法求函数的最值,即若f(x)在[a,b]上递增,则f(x)的最大值为f(b),最小值为f(a);若f(x)在[a,b]上递减,则f(x)的最大值为f(a),最小值为f(b).
例如,函数f(x)=x3在[-1,3]上为增函数,则f(x)在[-1,3]上的最小值为f(-1)=-1,最大值为f(3)=27.
求函数????(????)=13????3?4????+4在区间[0,3]上的最大值与最小值.
?
解:由已知可知,在区间[0,3]上,当????=2时,函数????(????)=13????3?4????+4有极小值,并且极小值为????(2)=?43.
又由于????(0)=4,????(3)=1,
所以,函数????(????)=13????3?4????+4在区间[0,3]上的最大值是4,最小值是?43.
上述结论可以从函数????(????)=13????3?4????+4在区间[0,3]上的图象得到直观验证.
?
即时巩固
典例剖析
例1已知函数y=f(x)的导函数f ′(x)的图像如图所示,则下列判断正确的是( )
A.函数y=f(x)在区间?3,?12内单调递增
B.当x=-2时,函数y=f(x)取得极小值
C.函数y=f(x)在区间(-2,2)内单调递增
D.当x=3时,函数y=f(x)有极小值
?
解析 对于A,函数y=f(x)在区间?3,?12内有增有减,故A不正确;对于B,当x=-2时,函数y=f(x)取得极小值,故B正确;对于C,当x∈(-2,2)时,恒有f ′(x)>0,则函数y=f(x)在区间(-2,2)上单调递增,故C正确;对于D,当x=3时,f ′(x)≠0,故D不正确.
答案 BC
?
例2 设f(x)=ax3+bx+c为奇函数,且其图像在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f ′(x)的最小值为-12.
(1)求a,b,c的值.
(2)求函数f(x)在[-2,3]上的极大值和极小值.
解题提示 (1)先根据奇函数求出c的值,再根据导函数f ′(x)的最小值求出b的值,最后依据在x=1处的导数等于切线的斜率求出a的值即可;
(2)先求导数f ′(x),在函数的定义域内解不等式f ′(x)>0和f ′(x)<0,求得区间即为单调区间,进而得到函数的极值.
解 (1)∵ f(x)为奇函数,∴ f(-x)=-f(x),即-ax3-bx+c=-ax3-bx-c,∴ c=0.
∵ f ′(x)=3ax2+b的最小值为-12,∴ b=-12.
又直线x-6y-7=0的斜率为16,
∴ f ′(1)=3a+b=-6,∴ a=2,b=-12,c=0.
(2)f(x)=2x3-12x,f ′(x)=6(x+2)(x-2),
令f ′(x)=0得x=-2或x=2,
当x变化时,f ′(x),f(x)的变化情况如下表:
∴ 函数f(x)的单调增区间是[-2,-2)和(2,3],函数f(x)的单调递减区间是(-2,2),
∴ f(x)在[-2,3]上的极大值是f(-2)=82,极小值是f(2)=-82.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
[-2,-2)
-2
(-2,2)
2
(2,3]
f ′(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
f ′(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
规律总结
求函数f(x)极值的步骤
(1)确定函数的定义域;
(2)求导数f ′(x);
(3)解方程f ′(x)=0,求出函数在定义域内的所有根;
(4)列表观察f ′(x)在f ′(x)=0的根x0左右两侧值的符号,如果左正右负(左增右减),那么f(x)在x0处取极大值,如果左负右正(左减右增),那么f(x)在x0处取极小值;
(5)如果只有一个极值点,则在该处既是极值也是最值.
例3 若函数f(x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,则实数a的取值范围为( )
A.-1
解题提示 先求导函数,根据函数f (x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,可得f ′(x)=3x2+6ax+3(a+2)=0有两个不等的实数根,从而可以求得实数a的取值范围.
解析 ∵ f(x)=x3+3ax2+3(a+2)x+1,∴ f ′(x)=3x2+6ax+3(a+2).
∵ 函数f(x)=x3+3ax2+3(a+2)x+1既有极大值又有极小值,
∴ f ′(x) =3x2+6ax+3(a+2)=0有两个不等的实数根,
∴ 36a2-36(a+2)>0,即a2-a-2>0,
解得a<-1或a>2,
答案 D
规律总结
逆向应用函数的极值,主要是含参数的问题,应注意两个方面:
一是注意对参数的分类讨论,要抓住讨论的切入点;
二是一般要对结果进行检验,以验证充分必要性.
例4 已知函数f(x)=x-2????-3ln x+1.
(1)求函数f(x)的单调区间;
(2)求f(x)在区间[1,e2]上的值域.
?
解题提示
(1)函数f(x)的定义域是(0,+∞),f '(x)=1+2????2-3????=????2?3????+2????2=?????1?????2????2,
可得当x变化时,f '(x),f(x)的变化情况,进而得出函数f(x)的单调区间;
(2)由(1)可知在区间(1,e2)内,当x=2时,f(x)取得极小值,可得
f(2)
解 (1)函数f(x)的定义域是(0,+∞),
f '(x)=1+2????2-3????=????2?3????+2????2=?????1?????2????2.
当x变化时,f '(x),f(x)的变化情况如下表:
所以f(x)在(0,1)和(2,+∞)上单调递增,在(1,2)上单调递减.
(2)由(1)可知在区间(1,e2)内,当x=2时,f(x)取得极小值 ,
f(1)=0,f(2)=2-3ln 2,f(e2)=e2-2e2-5,
得f(2)
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(0,1)
1
(1,2)
2
(2,+∞)
f '(x)
+
0
-
0
+
f(x)
↗
极大值
↘
极小值
↗
类题通法
求函数f(x)最值的基本步骤
(1)求导函数:求函数f(x)的导函数f ′(x).
(2)求极值可疑点:即求出f ′(x)不存在的点或f ′(x)=0的点.
(3)列表:依极值可疑点将函数的定义域分成若干个子区间,列出f ′(x)与f(x)随x变化的一览表.
(4)求极值:依(3)的表中所反映的相关信息,求出f(x)的极值点和极值.
(5)求区间端点函数值.
(6)求最值:比较极值可疑点和区间端点的函数值后,得出函数f(x)在其定义域内的最大值和最小值.
一般地,最大(小)值是由区间端点的函数值和极大(小)(包括导数不存在的点)值比较而得.
例5 已知函数f(x)=ex-3x+3a(e为自然对数的底数,a∈R).
(1)求f(x)的单调区间与极值;
(2)求证:当a>ln3e,且x>0时,e???????? >32x-3a+1????.
?
解题提示
(1)先求出f ′(x)>0,f ′(x)<0分别可得递增区间和递减区间,代值计算,可得结果.
(2)通过构造函数g(x)=ex-32x2+3ax-1,利用导数结合(1)的结论,可知g(x)在(0,+∞)上单调递增,然后根据g(x)>g(0),可得结果.
?
(1)解:由f(x)=ex-3x+3a,知f ′(x)=ex-3.
令f ′(x)=0,得x=ln 3,
于是当x变化时,f ′(x),f(x)的变化情况如下表:
故f(x)的单调递减区间是(-∞,ln 3],单调递增区间是[ln 3,+∞),
f(x)在x=ln 3处取得极小值,极小值为f (ln 3)=eln 3-3ln 3+3a=3-3ln 3+3a. 无极大值.
(2)证明:待证不等式等价于ex>32x2-3ax+1,
设g(x)=ex-32x2+3ax-1,x>0,于是g′(x)=ex-3x+3a,x>0.
由(1)及a>ln3e=ln 3-1知:g′(x)的最小值为g′(ln 3)=3(1-ln 3+a)>0.
于是对任意x>0,都有g′(x)>0,所以g(x)在(0,+∞)内单调递增.
于是当a>ln3e=ln 3-1时,对任意x∈(0,+∞),都有g(x)>g(0).
而g(0)=0,从而对任意x∈(0,+∞),g(x)>0. 即ex>32x2-3ax+1,故e????????>32x-3a+1????.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(-∞,ln 3)
ln 3
(ln 3,+∞)
f ′(x)
-
0
+
f(x)
?
极小值
?
类题通法
构造函数法证明不等式中常见的方法
(1)移项法:证明不等式f(x)>g(x)(f(x)
(2)构造“形似”函数:对原不等式同解变形,如移项、通分、取对数;把不等式转化为左右两边是相同结构的式子的结构,根据“相同结构”构造辅助函数.
(3)放缩法:若所构造函数最值不易求解,可将所证明的不等式进行放缩,再重新构造函数.
例6 已知函数f (x)=xex-????12????2+????(a∈R).
(1)当a=0时,求函数f(x)的极值;
(2)若?x∈(-2,0),f(x)≤0恒成立,求实数a的取值范围.
?
解 (1)当a=0时,f ′(x)=(x+1)ex,当x<-1时f ′(x)<0;当x>-1时f ′(x)>0,
∴ f(x)在(-∞,-1)上单调递减,在(-1,+∞)上单调递增.
∴ f(x)的极小值为f(-1)=-1e,无极大值.
(2)∵ 对?x∈(-2,0),f(x)≤0恒成立,∴ a≤2e????????+2在(-2,0)上恒成立.
令g(x)=2e????????+2(-2
∴ g(x)在(-2,-1)上单调递减,在(-1,0)上单调递增,
∴ g(x)min=g(-1)=2e?1?1+2=2e,∴ 实数a的取值范围为?∞,2e.
?
类题通法
不等式恒(能)成立的求解策略
“恒成立”与“存在性”问题的求解是“互补”关系,即f(x)≥g(x)对于x∈D恒成立,应求f(x)的最小值;若存在x∈D,使得f(x)≥g(x)成立,应求f(x)的最大值.在具体问题中究竟是求最大值还是最小值,可以先联想“恒成立”是求最大值还是最小值,这样就可以解决相应的“存在性”问题是求最大值还是最小值,特别需要关注等号是否成立问题,以免细节出错.
例7 设函数f(x)=????22-kln x,k>0.
(1)求f(x)的单调区间和极值;
(2)证明:若f(x)存在零点,则f(x)在区间(1,e]上仅有一个零点.
?
解题提示
(1)对函数f(x)求导,根据导数的正负确定函数的单调区间和极值;
(2)根据(1)中函数的单调性和极值分析函数图像,得出最值,进而得出函数存在零点时k的取值范围,由此结合零点存在性定理进行证明.
(1)解:由f(x)=????22-kln x(k>0,x>0)得f ′(x)=x-????????=????2?????????,由f ′(x)=0,解得x=????.
当x变化时,f ′(x)与f(x)在区间(0,+∞)上的变化情况如下表:
所以f(x)的单调递减区间是(0,????),单调递增区间是(????,+∞),x=????处取得极小值f(????)=????1?ln?????2.
(2)证明:由(1)知,f(x)在区间(0,+∞)上的最小值为f(????)=????1?ln?????2.
因为f(x)存在零点,所以????1?ln?????2≤0,从而k≥e.
当k=e时,f(x)在区间(1,e)上单调递减,且f(e)=0,所以x=e是f(x)在区间(1,e]上的唯一零点.
当k>e时,f(x)在区间(1,e)上单调递减,且f(1)=12>0,f(e)=e?????2<0,
所以f(x)在区间(1,e]上仅有一个零点.
综上可知,若f(x)存在零点,则f(x)在区间(1,e]上仅有一个零点.
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
(0,????)
????
(????,+∞)
f ′(x)
-
0
+
f(x)
?
????1?ln?????2
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
f ′(x)
-
0
+
f(x)
?
?
类题通法
利用导数研究零点的个数
函数的零点个数也就是函数图像与x轴交点的个数,所以可利用数形结合的方法判断交点个数,如果函数较为复杂,可结合导数知识确定极值点和单调区间从而确定其函数的大致图像.对于含参函数的零点个数,一般可从两个方面讨论:一是利用导数研究函数的单调性和极值,作出函数的大致图像,根据极大值和极小值的符号确定函数零点的个数;二是分离参数,将问题转化为求y=a和y=f(x)的图像的交点个数问题求解.
随堂小测
1.函数????(????)的导函数????=?????′(????)的图象如图所示, 其中?3,2,4是?????′(????)=0的根, 现给出下列命题:
①????(4)是????(????)的极小值;
②????(2)是????(????)的极大值;
③????(?2)是????(????)的极大值;
④????(3)是????(????)的极小值;
⑤????(?3)是????(????)的极大值.
其中正确的命题是 .(填上正确命题的序号)
?
①②
2.若函数????(????)=????3+????????2+????????+????2在????=1处取得极值10,则????= ,????= .
?
4
?11
?
3.若函数????(????)=????3+3????????2+3[(????+2)????+1]既有极大值又有极小值,则????的取值范围是 .
?
(?∞,?1)∪(2,+∞)
?
4.已知函数????(????)=?????2?????3ln?????+1.
(1)求函数????(????)的单调区间;
(2)求????(????)在区间[1,????2]上的值域.
?
(1)单调递增区间为(0,1),(2,+∞),单调递减区间为(1,2).
?
(2)????(????)在区间[1,e2]上的值域为
?
5.设a>0且a为常数,求函数y=e-x-e-2x在区间[0,a]上的最大值和最小值.
解:y′=-e-x+2e-2x=-e-2x(ex-2).
令y′=0,得x=ln 2.
因为x∈[0,a],所以只需研究x≥0的情况,如下表:
又y=e-x-e-2x=e-2x(ex-1),当x>0时,ex-1>0,所以此时y>0.
由上可知:若0
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
(0,ln 2)
ln 2
(ln 2,+∞)
y′
?
+
0
-
y
0
?
14
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
(0,ln 2)
ln 2
(ln 2,+∞)
y′
?
+
0
-
y
0
?
?
6.设函数f(x)=x3+4x2+4x+c.若函数f(x)有三个不同零点,求c的取值范围.
解:由题意知,f ′(x)=3x2+8x+4.
令f ′(x)=0,得3x2+8x+4=0,解得x=-2或x=-23.
当x变化时,f ′(x)与f(x)的变化情况如下表:
所以,当c>0且c-3227<0,即0
?
课堂小结
1.求函数????=????(????)的极值的方法:
解方程?????′(????)=0,当?????′(????0)=0时:
(1)如果在????0附近的左侧?????′(????)>0,右侧?????′(????)<0,那么????(????0)是极大值;
(2)如果在????0附近的左侧?????′(????)<0,右侧?????′(????)>0,那么????(????0)是极小值.
?
2.求函数????=????(????)在区间[????,????]上的最大值与最小值的步骤:
(1)求函数????=????(????)在区间(????,????)上的极值;
(2)将函数????=????(????)的各极值与端点处的函数值????(????),????(????)比较,其中最大的一个是最大值,最小的一个是最小值.
?
课堂小结
知识清单:
函数的极值;利用单数研究函数的最值;
方法归纳:函数最值的求法:求导数-求可能极值点-列表-求极值-求区间端点的函数值-求最值.
常见误区:对函数极值与最值的关系理解不透
谢 谢!
