5.2.1 基本初等函数的导数 教学设计
文档属性
| 名称 | 5.2.1 基本初等函数的导数 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 644.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 14:39:09 | ||
图片预览




文档简介
5.2.1 基本初等函数的导数
内容:
巩固理解导数的概念,学习导数的几何意义
内容分析:
导数是微积分的核心内容之一,是现代数学的基础概念.导数定量地刻画了函数的局部变化,是研究函数增减、变化快慢、最大、小值等性质的基本方法,也是解决增长率、膨胀率、效率、密度、速度、加速度等实际问题的基本工具.
导数的本质是函数的瞬时变化率,即函数平均变化率的极限,通过由割线斜率过渡到切线斜率的过程,由平均变化率的极限引出瞬时变化率,进而建立导数的概念,理解导数概念的几何意义.
极限是人们从微观层面认识世界变化规律的重要工具,导数是一种特殊的极限,蕴含着极限的思想,理解导数的定义,对于发展同学们的数学抽象思想和正确的世界观有着重要的作用.导数的几何意义表明,函数在某点处的导数是函数在相应点处切线的斜率,对于帮助学生理解导数的定义,提升数学能力,发展直观思想素养,有重要的作用.
教学目标:
掌握基本初等函数的导数公式.
学会利用公式求一些函数的导数.
教学重点、难点:
重点:基本初等函数的导数公式及公式的推导过程.
难点:基本初等函数的导数公式及公式推导过程及应用.
三、教学过程设计
(一)旧知回顾
引导学生回顾复习。
1、导数的定义
对于函数,设自变量从变化到,相应地,函数值就从 变化到,的变化量为,的变化量为
我们把比值,即
叫做函数从到的平均变化率.
当时,平均变化率无限接近一个确定的值,即有极限,则称 在处可导,并把这个确定的值叫做在处的导数(也称瞬时变化率),
记作或,即
.
从求函数在处导数的过程可以看到,当时,是一个唯一确定的数,这样,当变化时,就是的函数,称它为的导函数,记作:
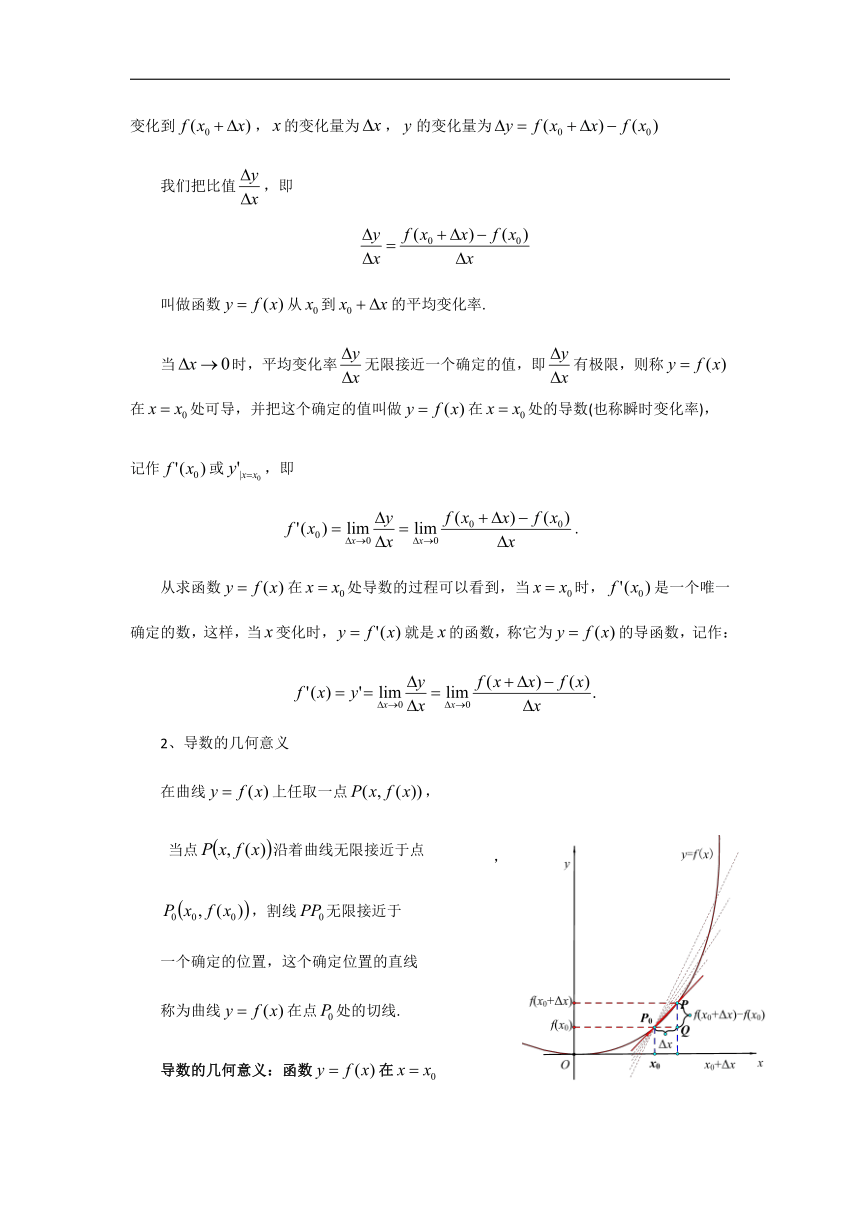
2、导数的几何意义
在曲线上任取一点,
当点沿着曲线无限接近于点 ,
,割线无限接近于
一个确定的位置,这个确定位置的直线
称为曲线在点处的切线.
导数的几何意义:函数在
处切线的斜率.
.
求函数导数的步骤:
求函数的变化量:;
求平均变化率:;
求导数:.
新知学习
根据导数的定义,求函数的导数,就是求出当时,无限趋近的那个定值.下面我们求几个常用函数的导数.
函数的导数:
因为,
所以,,
若表示路程关于时间的函数,则可以解释为物体瞬时速度始终为0,即一直处于静止状态.
函数的函数
因为
所以
若表示路程关于时间的函数,则可以解释为某物体做瞬时速度为1的匀速直线运动.
3、函数的导数
因为
所以
表示函数的图象上点处切线的斜率为说明随着的变化,切线的斜率也在变化.
另一方面,从导数作为函数在一点的瞬时变化率来看,表明:
当时,随着的增加,越来越小,减少得越来越慢;
函数的导数
因为
所以
表示函数的图象上点处切线的斜率为,这说明随着的变化,切线的斜率也在变化,且恒为非负数.
5.函数的导数
因为
所以
探究 :函数的图象,根据图象,描述它的变化情况,并要求曲线在点(1,1)处的切线方程.
结合函数的图象及其导数发现:
当x<0时,随着x的增加,函数 减少得越来越快;
当x>0时,随着x的增加,函数 减少得越来越慢.
所以曲线在点(1,1)处切线的斜率为-1,
在点(1,1)处切线的切线方程:
6.函数的导数
因为
所以
前面我们根据导数的定义求出了一些常用函数的导数,一般地,有下面的基本初等函数的导数公式表,这些公式可以直接使用.
三、反馈与评价
求下列函数的导数:
4求曲线在点(4,2)处的切线方程.
四、课堂总结
1.导数的定义
对于函数,设自变量从变化到,相应地,函数值就从 变化到,的变化量为, 的变化量为
我们把比值,即
叫做函数从到的平均变化率.
当时,平均变化率无限接近一个确定的值,即有极限,则称 在处可导,并把这个确定的值叫做在处的导数(也称瞬时变化率),
记作或,即
.
作业:课本75页1,2,3
内容:
巩固理解导数的概念,学习导数的几何意义
内容分析:
导数是微积分的核心内容之一,是现代数学的基础概念.导数定量地刻画了函数的局部变化,是研究函数增减、变化快慢、最大、小值等性质的基本方法,也是解决增长率、膨胀率、效率、密度、速度、加速度等实际问题的基本工具.
导数的本质是函数的瞬时变化率,即函数平均变化率的极限,通过由割线斜率过渡到切线斜率的过程,由平均变化率的极限引出瞬时变化率,进而建立导数的概念,理解导数概念的几何意义.
极限是人们从微观层面认识世界变化规律的重要工具,导数是一种特殊的极限,蕴含着极限的思想,理解导数的定义,对于发展同学们的数学抽象思想和正确的世界观有着重要的作用.导数的几何意义表明,函数在某点处的导数是函数在相应点处切线的斜率,对于帮助学生理解导数的定义,提升数学能力,发展直观思想素养,有重要的作用.
教学目标:
掌握基本初等函数的导数公式.
学会利用公式求一些函数的导数.
教学重点、难点:
重点:基本初等函数的导数公式及公式的推导过程.
难点:基本初等函数的导数公式及公式推导过程及应用.
三、教学过程设计
(一)旧知回顾
引导学生回顾复习。
1、导数的定义
对于函数,设自变量从变化到,相应地,函数值就从 变化到,的变化量为,的变化量为
我们把比值,即
叫做函数从到的平均变化率.
当时,平均变化率无限接近一个确定的值,即有极限,则称 在处可导,并把这个确定的值叫做在处的导数(也称瞬时变化率),
记作或,即
.
从求函数在处导数的过程可以看到,当时,是一个唯一确定的数,这样,当变化时,就是的函数,称它为的导函数,记作:
2、导数的几何意义
在曲线上任取一点,
当点沿着曲线无限接近于点 ,
,割线无限接近于
一个确定的位置,这个确定位置的直线
称为曲线在点处的切线.
导数的几何意义:函数在
处切线的斜率.
.
求函数导数的步骤:
求函数的变化量:;
求平均变化率:;
求导数:.
新知学习
根据导数的定义,求函数的导数,就是求出当时,无限趋近的那个定值.下面我们求几个常用函数的导数.
函数的导数:
因为,
所以,,
若表示路程关于时间的函数,则可以解释为物体瞬时速度始终为0,即一直处于静止状态.
函数的函数
因为
所以
若表示路程关于时间的函数,则可以解释为某物体做瞬时速度为1的匀速直线运动.
3、函数的导数
因为
所以
表示函数的图象上点处切线的斜率为说明随着的变化,切线的斜率也在变化.
另一方面,从导数作为函数在一点的瞬时变化率来看,表明:
当时,随着的增加,越来越小,减少得越来越慢;
函数的导数
因为
所以
表示函数的图象上点处切线的斜率为,这说明随着的变化,切线的斜率也在变化,且恒为非负数.
5.函数的导数
因为
所以
探究 :函数的图象,根据图象,描述它的变化情况,并要求曲线在点(1,1)处的切线方程.
结合函数的图象及其导数发现:
当x<0时,随着x的增加,函数 减少得越来越快;
当x>0时,随着x的增加,函数 减少得越来越慢.
所以曲线在点(1,1)处切线的斜率为-1,
在点(1,1)处切线的切线方程:
6.函数的导数
因为
所以
前面我们根据导数的定义求出了一些常用函数的导数,一般地,有下面的基本初等函数的导数公式表,这些公式可以直接使用.
三、反馈与评价
求下列函数的导数:
4求曲线在点(4,2)处的切线方程.
四、课堂总结
1.导数的定义
对于函数,设自变量从变化到,相应地,函数值就从 变化到,的变化量为, 的变化量为
我们把比值,即
叫做函数从到的平均变化率.
当时,平均变化率无限接近一个确定的值,即有极限,则称 在处可导,并把这个确定的值叫做在处的导数(也称瞬时变化率),
记作或,即
.
作业:课本75页1,2,3
