华东师大版数学七年级上册 第4章 图形的初步认识 小结与复习课件(共23张PPT)
文档属性
| 名称 | 华东师大版数学七年级上册 第4章 图形的初步认识 小结与复习课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 21:03:39 | ||
图片预览







文档简介
(共23张PPT)
小结与复习
第4章 图形的初步认识
要点梳理
二、立体图形的视图
一、立体图形
围成棱柱和棱锥等立体图形的面是平的面.
像这样的立体图形,又称为多面体 .
立体图形可以分为柱体、锥体、球体三大类.
1.三视图位置有规定,主视图要在左上边,它下方应
是俯视图,左视图坐落在右三边.
2.画三视图时,三个视图要放在正确的位置,并且使主视
图与俯视图的长对正,主视图与左视图高平齐,左视
图与俯视图的宽相等.
3.由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
名称 立体图形 表面展开图 底面形状 侧面形状 侧面展开
图的形状
正方体 正方形 正方形 正方形
长方体 长方形 长方形 长方形
五棱柱 五边形 长方形 长方形
圆柱 圆 曲面 长方形
圆锥 圆 曲面 扇形
三、立体图形的表面展开图
四、平面图形
由线段围成的封闭图形叫做多边形.
由于圆是由曲线围成的封闭图形,所以圆不是多边形.
五、最基本的图形
两点确定一条直线
两点之间,线段最短
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
线段和角的大小比较:度量法、叠合法.
同角(等角)的补角相等
同角(等角)的余角相等
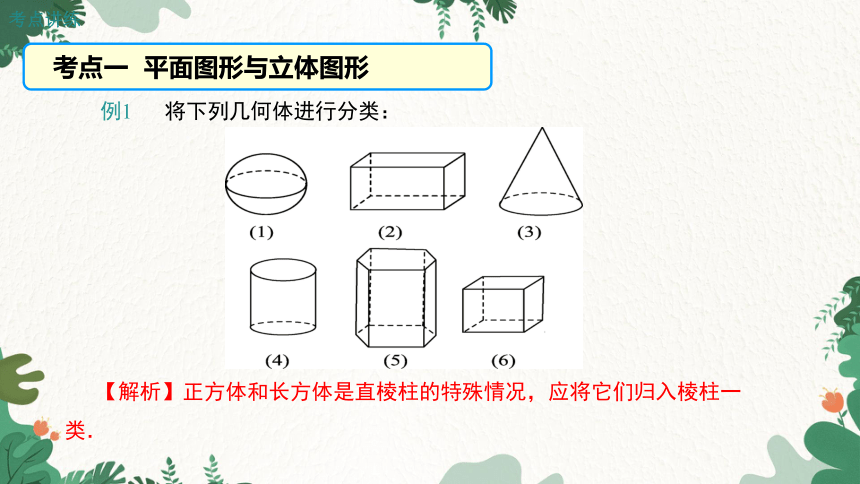
例1 将下列几何体进行分类:
【解析】正方体和长方体是直棱柱的特殊情况,应将它们归入棱柱一类.
考点讲练
考点一 平面图形与立体图形
解:若按这个几何体是柱体、锥体和球体划分:(2)(4)(5)(6)为一类,它们都是柱体;(3)为一类,它是锥体;(1)为一类,它是球体.
若按围成这个几何体的表面是平面还是曲面来分:(2)(5)(6)为一类,围成它们的表面都是平面;(1)(3)(4)为一类,围成它们的表面中至少有一个曲面.
在对几何体进行分类时要做到不重不漏,分类合理.
方法总结
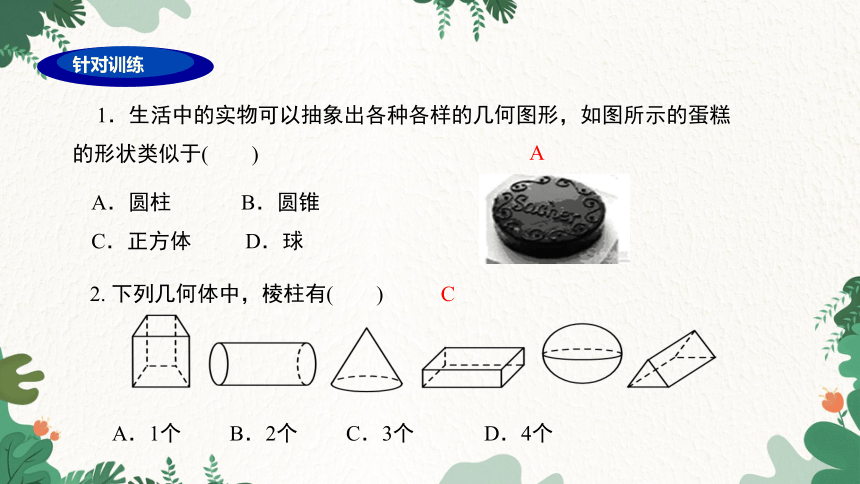
针对训练
A
1.生活中的实物可以抽象出各种各样的几何图形,如图所示的蛋糕的形状类似于( )
A.圆柱 B.圆锥
C.正方体 D.球
A.1个 B.2个 C.3个 D.4个
2. 下列几何体中,棱柱有( )
C
例2 一个几何体由几个大小相同的小立方块搭成,从上面和从左面看到的形状图如图所示.请搭出满足条件的几何体.你搭的几何体由几个小立方块搭成?
从上面看
从左面看
考点二 立体图形的视图与表面展开图
从上面看
从左面看
解:由于从上面看到的是几何体底层情况,从左面看到的是每行的最高层数.
所以该几何体有以下可能:
由小方块搭成的几何体画从正面、左面和上面三个不同的方向看到的图形,关键是确定它们有几列,以及每列方块的个数.
2.由从正面、左面和上面三个不同的方向看到的图形,画出原几何体.
(1)先由从上面看到的图形画出几何体底层;
(2)再由从正面、左面看到的图形,确定每列每行的层数.
方法总结
例3 如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对的面上的数相等,则图中x的值为_____.
【解析】解题的关键是找到折叠起来后的相对面.由展开图可知4的对面是y,7的对面是x,所以图中x的值为7.
7
我们知道,每一个正方体都是由三对相对的面围成的.在平面展开图中找相对的面是探索正方体展开图的关键.
方法总结
3.如图,从正面看A、B、C、D四个立体图形,分别得到a、b、c、d四个平面图形,把上下两行相对应立体图形与平面图形用线连接起来.
针对训练
5.如图所示,将图沿虚线折起来,得到一个正方体,那么“3”的对面是______.
4
1
2
6
5
3
6
4.下图中是正方体的展开图的有( )个
A.2个 B.3个 C.4个 D.5个
B
例4 如图,点C在线段AB上,
点M、N分别是AC、BC的中点.
(1)AC = 8 cm,CB = 6 cm,求线段MN的长;
【解析】根据“M、N分别是AC、BC的中点”,先求出MC,CN的长度,再利用MN=CM+CN即可求出MN的长度.
解:(1)∵点M、N分别是AC、BC的中点,∴CM= AC=4(cm),CN= BC=3(cm),∴MN=CM+CN=4+3=7 (cm);
考点三 线段的中点及相关长度的计算
(2)若C为线段AB上任一点,满足AC + CB = a cm,其它条件不变,你能猜想MN的长度吗?并说明理由.
解:(2)同(1)可得
CM= AC ,CN= BC,
∴MN=CM+CN
= AC+ BC
= (AC+BC)= a (cm)
(3)若C在线段AB的延长线上,且满足AC-BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.
解:MN的长度等于 bcm. 根据题意画出图形,
由图可得
MN=MC-NC= AC- BC
= (AC-BC)= b(cm).
6.点A,B,C 在同一条直线上,AB=3 cm,
BC=1 cm.求AC的长.
解:(1)如图①,因AB=3cm,BC=1cm,
所以,AC=AB+BC=3+1=4(cm).
(2)如图②,AC=AB-BC=3-1=2(cm).
【解析】因点A,B,C的顺序不确定,所以要考虑B在线段AC上,B在线段AC的延长线上两种情况 .
针对训练
考点四 角的度量及角度的计算
例5 45°52′48″=______°;
126.31°= ____°____′____″;
25°18′÷3=__________;
126.31 =126 +0.31×60′=126 +18.6′
=126 18′+0.6×60″=126 18′36″
解:45°52′48″=45°+52′+(48÷60)′=45°+52.8′
=45 +(52.8÷60)°=45.88
25°18′÷3=8°+1°18′÷3=8°+78′÷3=8°26′
例6 如图,∠AOB是直角, ∠AOC=50°,ON是∠AOC的平分线,OM是∠BOC的平分线.求∠MON的大小.
O
B
M
A
N
C
【解析】先求出∠BOC的度数,再根据角平分线的定义求出∠COM,∠CON,然后根据∠MON=∠COM-∠CON代入数据进行计算即可得解.
解:∵∠AOB是直角,∠AOC=50°, ∴∠BOC=∠AOB+∠AOC=90°+50°=140°, ∵ON是∠AOC的平分线,OM是∠BOC的平分线, ∴∠COM=70°,∠CON=25°, ∴∠MON=∠COM-∠CON=70°-25°=45°;
7.若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
A
针对训练
8.点整时,时钟上时针与分钟 之间的夹角是( )
A.210° B.30° C.150° D.60°
C
考点五 余角和补角
例7 已知∠α和∠β互为补角,并且∠β的一半比∠α小30 ,求∠α、∠β.
解:设∠α=x ,则∠β=180 -x .
根据题意 ∠β=2(∠α-30 ),
得 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80 ,∠β=100 .
【解析】设∠α=x ,用x表示出∠β,列出方程即可.
课堂小结
立体图形
平面图形
几何图形
从不同方向看立体图形
展开立体图形
平面图形
直线、射线、线段
角
角的度量
角的比较与运算
余角和补角
角的平分线
线段大小的比较
两点确定一条直线
两点之间,线段最短
等(同)角的补角相等
等(同)角的余角相等
小结与复习
第4章 图形的初步认识
要点梳理
二、立体图形的视图
一、立体图形
围成棱柱和棱锥等立体图形的面是平的面.
像这样的立体图形,又称为多面体 .
立体图形可以分为柱体、锥体、球体三大类.
1.三视图位置有规定,主视图要在左上边,它下方应
是俯视图,左视图坐落在右三边.
2.画三视图时,三个视图要放在正确的位置,并且使主视
图与俯视图的长对正,主视图与左视图高平齐,左视
图与俯视图的宽相等.
3.由三视图描述几何体(或实物原型),一般步骤为:
① 想象:根据各视图想象从各个方向看到的几何体形状;
② 定形:综合确定几何体(或实物原型)的形状;
③ 定大小位置:根据三个视图“长对正,高平齐,宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸.
名称 立体图形 表面展开图 底面形状 侧面形状 侧面展开
图的形状
正方体 正方形 正方形 正方形
长方体 长方形 长方形 长方形
五棱柱 五边形 长方形 长方形
圆柱 圆 曲面 长方形
圆锥 圆 曲面 扇形
三、立体图形的表面展开图
四、平面图形
由线段围成的封闭图形叫做多边形.
由于圆是由曲线围成的封闭图形,所以圆不是多边形.
五、最基本的图形
两点确定一条直线
两点之间,线段最短
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
线段和角的大小比较:度量法、叠合法.
同角(等角)的补角相等
同角(等角)的余角相等
例1 将下列几何体进行分类:
【解析】正方体和长方体是直棱柱的特殊情况,应将它们归入棱柱一类.
考点讲练
考点一 平面图形与立体图形
解:若按这个几何体是柱体、锥体和球体划分:(2)(4)(5)(6)为一类,它们都是柱体;(3)为一类,它是锥体;(1)为一类,它是球体.
若按围成这个几何体的表面是平面还是曲面来分:(2)(5)(6)为一类,围成它们的表面都是平面;(1)(3)(4)为一类,围成它们的表面中至少有一个曲面.
在对几何体进行分类时要做到不重不漏,分类合理.
方法总结
针对训练
A
1.生活中的实物可以抽象出各种各样的几何图形,如图所示的蛋糕的形状类似于( )
A.圆柱 B.圆锥
C.正方体 D.球
A.1个 B.2个 C.3个 D.4个
2. 下列几何体中,棱柱有( )
C
例2 一个几何体由几个大小相同的小立方块搭成,从上面和从左面看到的形状图如图所示.请搭出满足条件的几何体.你搭的几何体由几个小立方块搭成?
从上面看
从左面看
考点二 立体图形的视图与表面展开图
从上面看
从左面看
解:由于从上面看到的是几何体底层情况,从左面看到的是每行的最高层数.
所以该几何体有以下可能:
由小方块搭成的几何体画从正面、左面和上面三个不同的方向看到的图形,关键是确定它们有几列,以及每列方块的个数.
2.由从正面、左面和上面三个不同的方向看到的图形,画出原几何体.
(1)先由从上面看到的图形画出几何体底层;
(2)再由从正面、左面看到的图形,确定每列每行的层数.
方法总结
例3 如图是一个正方体的侧面展开图,如果将它折叠成一个正方体后相对的面上的数相等,则图中x的值为_____.
【解析】解题的关键是找到折叠起来后的相对面.由展开图可知4的对面是y,7的对面是x,所以图中x的值为7.
7
我们知道,每一个正方体都是由三对相对的面围成的.在平面展开图中找相对的面是探索正方体展开图的关键.
方法总结
3.如图,从正面看A、B、C、D四个立体图形,分别得到a、b、c、d四个平面图形,把上下两行相对应立体图形与平面图形用线连接起来.
针对训练
5.如图所示,将图沿虚线折起来,得到一个正方体,那么“3”的对面是______.
4
1
2
6
5
3
6
4.下图中是正方体的展开图的有( )个
A.2个 B.3个 C.4个 D.5个
B
例4 如图,点C在线段AB上,
点M、N分别是AC、BC的中点.
(1)AC = 8 cm,CB = 6 cm,求线段MN的长;
【解析】根据“M、N分别是AC、BC的中点”,先求出MC,CN的长度,再利用MN=CM+CN即可求出MN的长度.
解:(1)∵点M、N分别是AC、BC的中点,∴CM= AC=4(cm),CN= BC=3(cm),∴MN=CM+CN=4+3=7 (cm);
考点三 线段的中点及相关长度的计算
(2)若C为线段AB上任一点,满足AC + CB = a cm,其它条件不变,你能猜想MN的长度吗?并说明理由.
解:(2)同(1)可得
CM= AC ,CN= BC,
∴MN=CM+CN
= AC+ BC
= (AC+BC)= a (cm)
(3)若C在线段AB的延长线上,且满足AC-BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.
解:MN的长度等于 bcm. 根据题意画出图形,
由图可得
MN=MC-NC= AC- BC
= (AC-BC)= b(cm).
6.点A,B,C 在同一条直线上,AB=3 cm,
BC=1 cm.求AC的长.
解:(1)如图①,因AB=3cm,BC=1cm,
所以,AC=AB+BC=3+1=4(cm).
(2)如图②,AC=AB-BC=3-1=2(cm).
【解析】因点A,B,C的顺序不确定,所以要考虑B在线段AC上,B在线段AC的延长线上两种情况 .
针对训练
考点四 角的度量及角度的计算
例5 45°52′48″=______°;
126.31°= ____°____′____″;
25°18′÷3=__________;
126.31 =126 +0.31×60′=126 +18.6′
=126 18′+0.6×60″=126 18′36″
解:45°52′48″=45°+52′+(48÷60)′=45°+52.8′
=45 +(52.8÷60)°=45.88
25°18′÷3=8°+1°18′÷3=8°+78′÷3=8°26′
例6 如图,∠AOB是直角, ∠AOC=50°,ON是∠AOC的平分线,OM是∠BOC的平分线.求∠MON的大小.
O
B
M
A
N
C
【解析】先求出∠BOC的度数,再根据角平分线的定义求出∠COM,∠CON,然后根据∠MON=∠COM-∠CON代入数据进行计算即可得解.
解:∵∠AOB是直角,∠AOC=50°, ∴∠BOC=∠AOB+∠AOC=90°+50°=140°, ∵ON是∠AOC的平分线,OM是∠BOC的平分线, ∴∠COM=70°,∠CON=25°, ∴∠MON=∠COM-∠CON=70°-25°=45°;
7.若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
A
针对训练
8.点整时,时钟上时针与分钟 之间的夹角是( )
A.210° B.30° C.150° D.60°
C
考点五 余角和补角
例7 已知∠α和∠β互为补角,并且∠β的一半比∠α小30 ,求∠α、∠β.
解:设∠α=x ,则∠β=180 -x .
根据题意 ∠β=2(∠α-30 ),
得 180- x=2(x -30),
解得 x=80.
所以 ,∠α=80 ,∠β=100 .
【解析】设∠α=x ,用x表示出∠β,列出方程即可.
课堂小结
立体图形
平面图形
几何图形
从不同方向看立体图形
展开立体图形
平面图形
直线、射线、线段
角
角的度量
角的比较与运算
余角和补角
角的平分线
线段大小的比较
两点确定一条直线
两点之间,线段最短
等(同)角的补角相等
等(同)角的余角相等
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
