4.5.2用二分法求方程的近似解 课件(共20张PPT)
文档属性
| 名称 | 4.5.2用二分法求方程的近似解 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 423.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 16:54:07 | ||
图片预览







文档简介
(共20张PPT)
4.5.2 用二分法求方程的近似解
明确目标 发展素养
1.通过具体实例理解二分法的概念及其使用条件. 2.了解二分法是求方程近似解的常用方法,能借助计算器用二分法求方程的近似解. 3.会用二分法求一个函数在给定区间内的零点,从而求得方程的近似解. 借助二分法的操作步骤与思想,培养数学建模和逻辑推理素养.
(一)教材梳理填空
1.二分法的概念:
对于在区间[a,b]上图象连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把它的 所在区间 ,使所得区间的两个 逐步逼近零点,进而得到零点近似值的方法叫做二分法.
零点
一分为二
端点
2.用二分法求函数零点近似值的步骤:
给定精确度ε,用二分法求函数y=f(x)零点x0的近似值的一般步骤如下:
(1)确定零点x0的初始区间[a,b],验证f(a)f(b)<0.
(2)求区间(a,b)的中点c.
(3)计算f(c),并进一步确定零点所在的区间:
①若f(c)=0(此时x0=c),则c就是函数的零点;
②若f(a)f(c)<0(此时x0∈(a,c)),则令___=c;
③若f(c)f(b)<0(此时x0∈(c,b)),则令___=c.
(4)判断是否达到精确度ε:若|a-b|<__,则得到零点近似值a(或b);否则重复步骤(2)~(4).
b
a
ε
[微思考] 用二分法求函数近似零点时,函数应满足哪些条件?
提示:(1)f(x)在区间[a,b]上的图象连续不断.
(2)在区间[a,b]端点的函数值f(a)·f(b)<0.
(二)基本知能小试
1.判断正误:
(1)所有函数的零点都可以用二分法来求. ( )
(2)函数f(x)=|x|可以用二分法求其零点. ( )
(3)精确度ε就是近似值. ( )
答案:(1)× (2)× (3)×
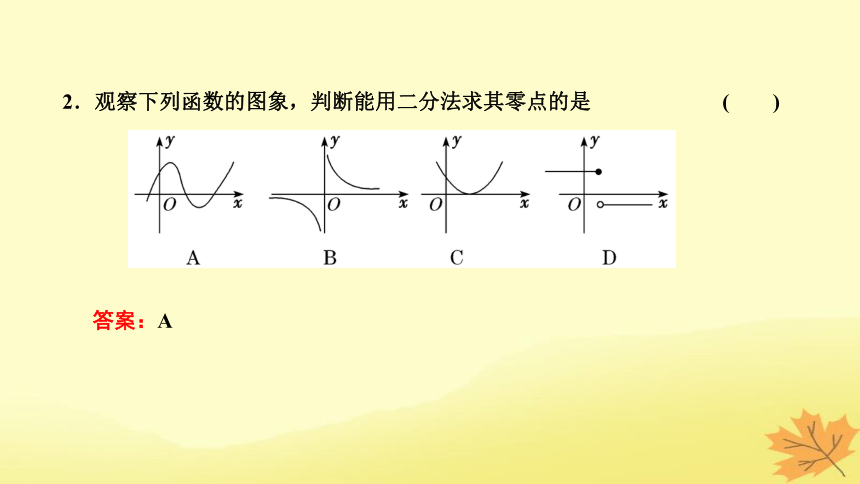
2.观察下列函数的图象,判断能用二分法求其零点的是 ( )
答案:A
3.用二分法研究函数f(x)=x3+3x-1的零点时,第一次经计算f(0)<0,f(0.5)>0,可得其中一个零点x0∈________,第二次应计算________,以上横线上应填的内容为 ( )
A.(0,0.5),f(0.25) B.(0,1),f(0.25)
C.(0.5,1),f(0.75) D.(0,0.5),f(0.125)
解析:二分法要不断地取区间的中点值进行计算.由f(0)<0,f(0.5)>0知x0∈(0,0.5).再计算0与0.5的中点0.25的函数值,以判断x0的更准确位置.故选A.
答案:A
题型一 二分法的概念
【学透用活】
二分就是将所给区间平均分成两部分,通过不断逼近的办法,找到零点附近足够小的区间,根据所要求的精确度,用此区间的某个数值近似地表示真正的零点.
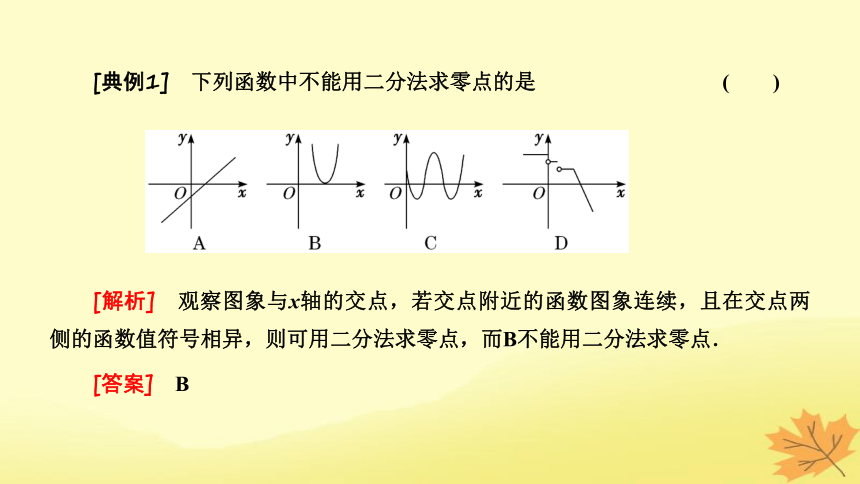
[典例1] 下列函数中不能用二分法求零点的是 ( )
[解析] 观察图象与x轴的交点,若交点附近的函数图象连续,且在交点两侧的函数值符号相异,则可用二分法求零点,而B不能用二分法求零点.
[答案] B
[方法技巧]
判断一个函数能否用二分法求其零点的依据是:其图象在零点附近是连续不断的,且该零点为变号零点.因此,用二分法求函数的零点近似值的方法仅对函数的变号零点适用,对函数的不变号零点不适用.
【对点练清】
1.已知函数f(x)的图象如图,其中零点的个数与可以用二分法求解
的个数分别为 ( )
A.4,4 B.3,4
C.5,4 D.4,3
解析:图象与x轴有4个交点,所以零点的个数为4;左右函数值异号的零点有3个,所以用二分法求解的个数为3,故选D.
答案:D
2.关于“二分法”求方程的近似解,下列说法正确的是 ( )
A.“二分法”求方程的近似解一定可将y=f(x)在[a,b]内的所有零点得到
B.“二分法”求方程的近似解有可能得不到y=f(x)在[a,b]内的零点
C.应用“二分法”求方程的近似解,y=f(x)在[a,b]内有可能无零点
D.“二分法”求方程的近似解也可能得到f(x)=0在[a,b]内的精确解
解析:如果函数在某区间满足二分法,且在区间内存在两个及以上的实根,二分法只可能求出其中的一个,∴A错误;二分法的实施满足零点存在定理,在区间内一定存在零点,∴B错误;C只要限定了近似解的范围就可以得到方程的近似解,∴C错误;“二分法”求方程的近似解,甚至有可能得到函数的精确零点,∴D正确.
答案:D
题型二 用二分法求方程的近似解
【学透用活】
用二分法求方程的近似解时的注意点
(1)明确题目要求的精确度.
(2)确定初始区间,一般在两个整数间,初始区间的长度越小,计算次数越少.
(3)按步骤依次进行计算,直至达到指定的精确度为止.
[典例2] 用二分法求方程2x3+3x-3=0的一个正实数近似解(精确度为0.1).
[解] 令f(x)=2x3+3x-3,
经计算,f(0)=-3<0,f(1)=2>0,f(0)·f(1)<0,
所以函数f(x)在(0,1)内存在零点,
即方程2x3+3x=3在(0,1)内有解.
取(0,1)的中点0.5,经计算f(0.5)<0,又f(1)>0,
所以方程2x3+3x-3=0在(0.5,1)内有解.
如此继续下去,得到方程的正实数根所在的区间,如下表:
由于|0.687 5-0.75|=0.062 5<0.1,所以0.75可作为方程的一个正实数近似解.
[方法技巧]
用二分法求方程的近似解应明确两点
(1)根据函数的零点与相应方程的解的关系,求函数的零点与求相应方程的解是等价的.求方程f(x)=0的近似解,即按照用二分法求函数零点近似值的步骤求解.
(2)对于求形如f(x)=g(x)的方程的近似解,可以通过移项转化成求形如F(x)=f(x)-g(x)=0的方程的近似解,然后按照用二分法求函数零点近似值的步骤求解.
【对点练清】
1.[变条件]若本例中的“精确度为0.1”换为“精确度为0.05”结论又如何?
解:在本例的基础上,取区间(0.687 5,0.75)的中点x=0.718 75,因为f(0.718 75)<0,f(0.75)>0且|0.718 75-0.75|=0.031 25<0.05,所以x=0.72可作为方程的一个近似解.
2.[变条件]若本例中的方程“2x3+3x-3=0”换为“x2-2x=1”其结论又如何呢?
解:设f(x)=x2-2x-1.∵f(2)=-1<0,f(3)=2>0,
∴在区间(2,3)内,方程x2-2x-1=0有一解,记为x0.
取2与3的平均数2.5,∵f(2.5)=0.25>0,∴2再取2与2.5的平均数2.25,
∵f(2.25)=-0.437 5<0,∴2.25如此继续下去,有f(2.375)<0,f(2.5)>0 x0∈(2.375,2.5);
f(2.375)<0,f(2.437 5)>0 x0∈(2.375,2.437 5).
∵|2.375-2.437 5|=0.062 5<0.1,∴方程x2=2x+1的一个精确度为0.1的近似解可取为2.437 5.
【课堂思维激活】
一、综合性——强调融会贯通
1.[好题共享——选自人教B版新教材]证明函数f(x)=x3-x2+5,x∈[-2,-1]有零点,并指出用二分法求零点的近似值(精确度小于0.1)时,至少需要进行多少次函数值的计算.
二、应用性——强调学以致用
2.在一个风雨交加的夜里,从某水库闸门到防洪指挥所的电话线路发生了故障,这是一条长为10 km,大约有200根电线杆的线路,请设计一个能迅速查出故障所在的方案,并回答维修线路的工人师傅最多检测几次就能找出故障地点所在区域(精确到100 m范围内)
[析题建模] 利用二分法原理进行查找,不妨设闸门与指挥所所处点为A,B,首先从AB的中点C处开始,判断AC是否正常,若AC正常,则故障在BC段,再取BC的中点,依此类推.
4.5.2 用二分法求方程的近似解
明确目标 发展素养
1.通过具体实例理解二分法的概念及其使用条件. 2.了解二分法是求方程近似解的常用方法,能借助计算器用二分法求方程的近似解. 3.会用二分法求一个函数在给定区间内的零点,从而求得方程的近似解. 借助二分法的操作步骤与思想,培养数学建模和逻辑推理素养.
(一)教材梳理填空
1.二分法的概念:
对于在区间[a,b]上图象连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把它的 所在区间 ,使所得区间的两个 逐步逼近零点,进而得到零点近似值的方法叫做二分法.
零点
一分为二
端点
2.用二分法求函数零点近似值的步骤:
给定精确度ε,用二分法求函数y=f(x)零点x0的近似值的一般步骤如下:
(1)确定零点x0的初始区间[a,b],验证f(a)f(b)<0.
(2)求区间(a,b)的中点c.
(3)计算f(c),并进一步确定零点所在的区间:
①若f(c)=0(此时x0=c),则c就是函数的零点;
②若f(a)f(c)<0(此时x0∈(a,c)),则令___=c;
③若f(c)f(b)<0(此时x0∈(c,b)),则令___=c.
(4)判断是否达到精确度ε:若|a-b|<__,则得到零点近似值a(或b);否则重复步骤(2)~(4).
b
a
ε
[微思考] 用二分法求函数近似零点时,函数应满足哪些条件?
提示:(1)f(x)在区间[a,b]上的图象连续不断.
(2)在区间[a,b]端点的函数值f(a)·f(b)<0.
(二)基本知能小试
1.判断正误:
(1)所有函数的零点都可以用二分法来求. ( )
(2)函数f(x)=|x|可以用二分法求其零点. ( )
(3)精确度ε就是近似值. ( )
答案:(1)× (2)× (3)×
2.观察下列函数的图象,判断能用二分法求其零点的是 ( )
答案:A
3.用二分法研究函数f(x)=x3+3x-1的零点时,第一次经计算f(0)<0,f(0.5)>0,可得其中一个零点x0∈________,第二次应计算________,以上横线上应填的内容为 ( )
A.(0,0.5),f(0.25) B.(0,1),f(0.25)
C.(0.5,1),f(0.75) D.(0,0.5),f(0.125)
解析:二分法要不断地取区间的中点值进行计算.由f(0)<0,f(0.5)>0知x0∈(0,0.5).再计算0与0.5的中点0.25的函数值,以判断x0的更准确位置.故选A.
答案:A
题型一 二分法的概念
【学透用活】
二分就是将所给区间平均分成两部分,通过不断逼近的办法,找到零点附近足够小的区间,根据所要求的精确度,用此区间的某个数值近似地表示真正的零点.
[典例1] 下列函数中不能用二分法求零点的是 ( )
[解析] 观察图象与x轴的交点,若交点附近的函数图象连续,且在交点两侧的函数值符号相异,则可用二分法求零点,而B不能用二分法求零点.
[答案] B
[方法技巧]
判断一个函数能否用二分法求其零点的依据是:其图象在零点附近是连续不断的,且该零点为变号零点.因此,用二分法求函数的零点近似值的方法仅对函数的变号零点适用,对函数的不变号零点不适用.
【对点练清】
1.已知函数f(x)的图象如图,其中零点的个数与可以用二分法求解
的个数分别为 ( )
A.4,4 B.3,4
C.5,4 D.4,3
解析:图象与x轴有4个交点,所以零点的个数为4;左右函数值异号的零点有3个,所以用二分法求解的个数为3,故选D.
答案:D
2.关于“二分法”求方程的近似解,下列说法正确的是 ( )
A.“二分法”求方程的近似解一定可将y=f(x)在[a,b]内的所有零点得到
B.“二分法”求方程的近似解有可能得不到y=f(x)在[a,b]内的零点
C.应用“二分法”求方程的近似解,y=f(x)在[a,b]内有可能无零点
D.“二分法”求方程的近似解也可能得到f(x)=0在[a,b]内的精确解
解析:如果函数在某区间满足二分法,且在区间内存在两个及以上的实根,二分法只可能求出其中的一个,∴A错误;二分法的实施满足零点存在定理,在区间内一定存在零点,∴B错误;C只要限定了近似解的范围就可以得到方程的近似解,∴C错误;“二分法”求方程的近似解,甚至有可能得到函数的精确零点,∴D正确.
答案:D
题型二 用二分法求方程的近似解
【学透用活】
用二分法求方程的近似解时的注意点
(1)明确题目要求的精确度.
(2)确定初始区间,一般在两个整数间,初始区间的长度越小,计算次数越少.
(3)按步骤依次进行计算,直至达到指定的精确度为止.
[典例2] 用二分法求方程2x3+3x-3=0的一个正实数近似解(精确度为0.1).
[解] 令f(x)=2x3+3x-3,
经计算,f(0)=-3<0,f(1)=2>0,f(0)·f(1)<0,
所以函数f(x)在(0,1)内存在零点,
即方程2x3+3x=3在(0,1)内有解.
取(0,1)的中点0.5,经计算f(0.5)<0,又f(1)>0,
所以方程2x3+3x-3=0在(0.5,1)内有解.
如此继续下去,得到方程的正实数根所在的区间,如下表:
由于|0.687 5-0.75|=0.062 5<0.1,所以0.75可作为方程的一个正实数近似解.
[方法技巧]
用二分法求方程的近似解应明确两点
(1)根据函数的零点与相应方程的解的关系,求函数的零点与求相应方程的解是等价的.求方程f(x)=0的近似解,即按照用二分法求函数零点近似值的步骤求解.
(2)对于求形如f(x)=g(x)的方程的近似解,可以通过移项转化成求形如F(x)=f(x)-g(x)=0的方程的近似解,然后按照用二分法求函数零点近似值的步骤求解.
【对点练清】
1.[变条件]若本例中的“精确度为0.1”换为“精确度为0.05”结论又如何?
解:在本例的基础上,取区间(0.687 5,0.75)的中点x=0.718 75,因为f(0.718 75)<0,f(0.75)>0且|0.718 75-0.75|=0.031 25<0.05,所以x=0.72可作为方程的一个近似解.
2.[变条件]若本例中的方程“2x3+3x-3=0”换为“x2-2x=1”其结论又如何呢?
解:设f(x)=x2-2x-1.∵f(2)=-1<0,f(3)=2>0,
∴在区间(2,3)内,方程x2-2x-1=0有一解,记为x0.
取2与3的平均数2.5,∵f(2.5)=0.25>0,∴2
∵f(2.25)=-0.437 5<0,∴2.25
f(2.375)<0,f(2.437 5)>0 x0∈(2.375,2.437 5).
∵|2.375-2.437 5|=0.062 5<0.1,∴方程x2=2x+1的一个精确度为0.1的近似解可取为2.437 5.
【课堂思维激活】
一、综合性——强调融会贯通
1.[好题共享——选自人教B版新教材]证明函数f(x)=x3-x2+5,x∈[-2,-1]有零点,并指出用二分法求零点的近似值(精确度小于0.1)时,至少需要进行多少次函数值的计算.
二、应用性——强调学以致用
2.在一个风雨交加的夜里,从某水库闸门到防洪指挥所的电话线路发生了故障,这是一条长为10 km,大约有200根电线杆的线路,请设计一个能迅速查出故障所在的方案,并回答维修线路的工人师傅最多检测几次就能找出故障地点所在区域(精确到100 m范围内)
[析题建模] 利用二分法原理进行查找,不妨设闸门与指挥所所处点为A,B,首先从AB的中点C处开始,判断AC是否正常,若AC正常,则故障在BC段,再取BC的中点,依此类推.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
