2022-2023学年人教版九年级数学上册23.1 图形的旋转第2课时 课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册23.1 图形的旋转第2课时 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 21:27:42 | ||
图片预览





文档简介
(共22张PPT)
23.1 图形的旋转
第2课时
学习目标
1.理解旋转的性质,了解旋转作图的步骤和关键.
2.能够根据旋转的性质作出常见图形的旋转图形.
3.通过观察、操作、交流、归纳等过程,培养学生探究问题的能力,动手能力和观察能力.
4. 经历探索旋转作图的过程,使学生充分感知数学美,培养学生学习数学的兴趣和热爱生活的情感.
图形的旋转
巩固新知
课堂小结
布置作业
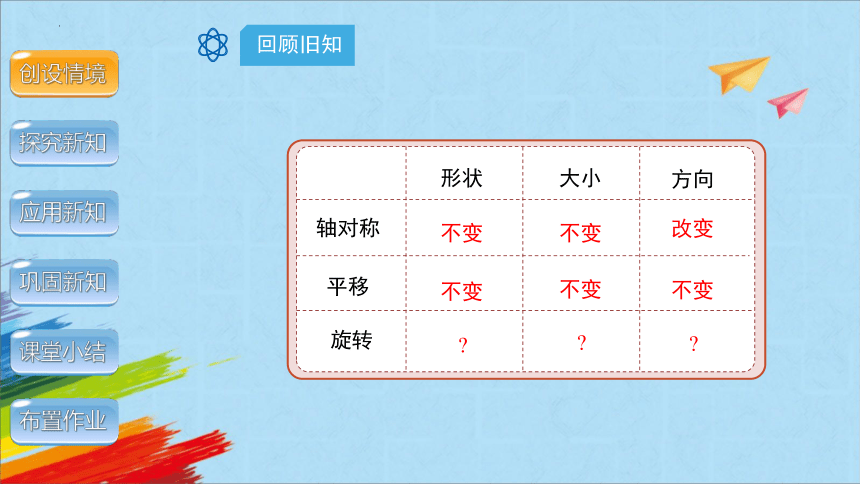
轴对称
平移
形状
大小
方向
旋转
不变
不变
不变
不变
改变
不变
应用新知
创设情境
探究新知
回顾旧知
应用新知
巩固新知
课堂小结
布置作业
探究
在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A'BC'),移开硬纸板.△A'B'C'是由△ABC绕点O旋转得到的.
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
A
B
C
A′
B′
C′
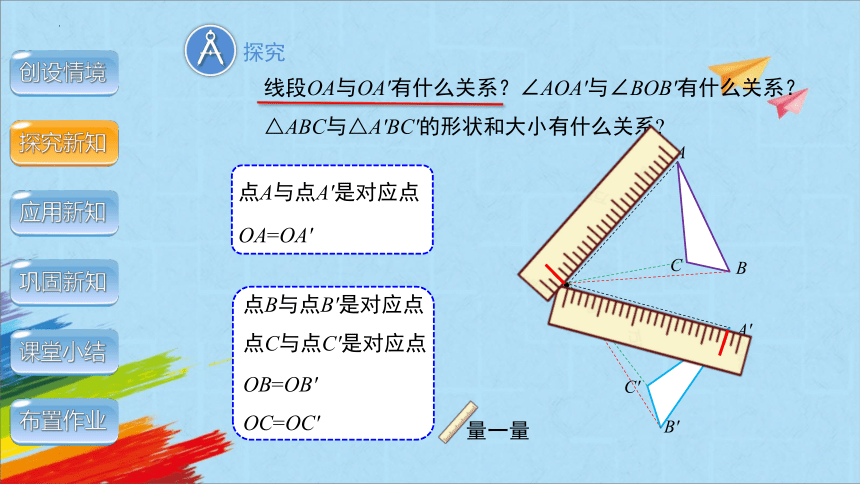
线段OA与OA'有什么关系?∠AOA'与∠BOB'有什么关系?△ABC与△A'BC'的形状和大小有什么关系
O
点A与点A'是对应点
OA=OA'
点B与点B'是对应点
点C与点C'是对应点
量一量
OB=OB'
OC=OC'
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
A
B
C
A′
B′
C′
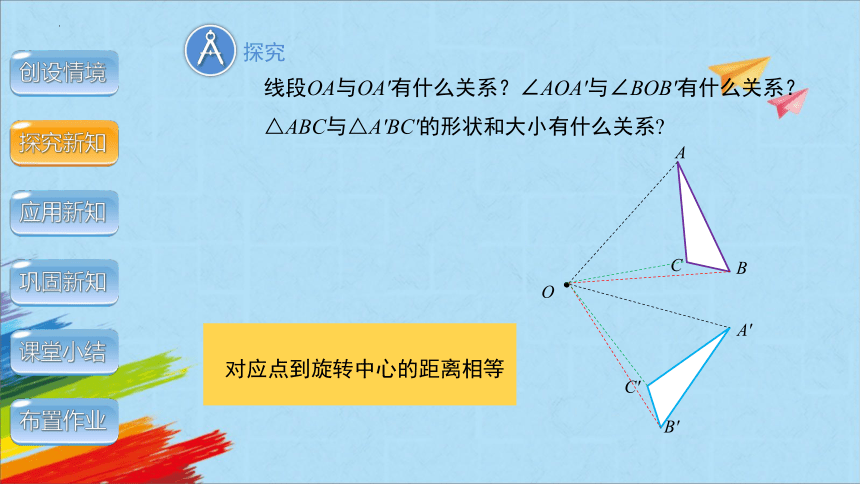
线段OA与OA'有什么关系?∠AOA'与∠BOB'有什么关系?△ABC与△A'BC'的形状和大小有什么关系
O
对应点到旋转中心的距离相等
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
A
B
C
A′
B′
C′
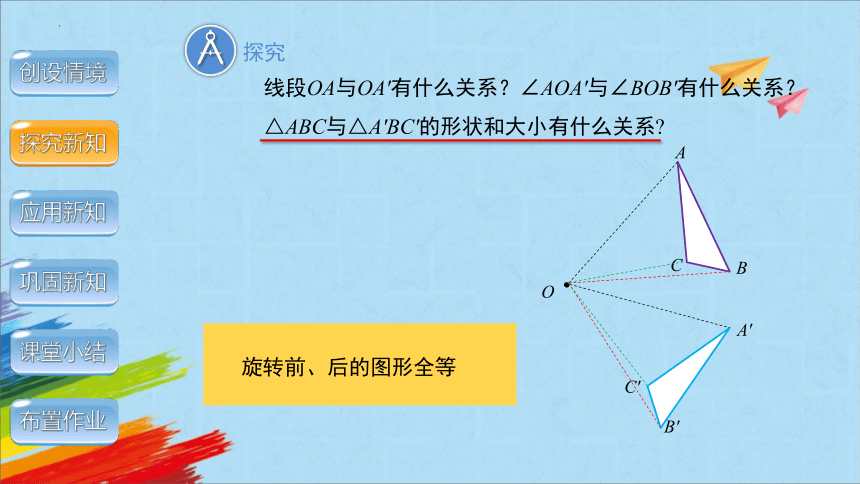
线段OA与OA'有什么关系?∠AOA'与∠BOB'有什么关系?△ABC与△A'BC'的形状和大小有什么关系
O
∠AOA'=∠BOB'
对应点与旋转中心所连线段的夹角都等于旋转角
量一量∠AOA'=∠COC'?
创设情境
探究新知
=∠COC'
应用新知
巩固新知
课堂小结
布置作业
探究
A
B
C
A′
B′
C′
线段OA与OA'有什么关系?∠AOA'与∠BOB'有什么关系?△ABC与△A'BC'的形状和大小有什么关系
O
旋转前、后的图形全等
创设情境
探究新知
巩固新知
课堂小结
布置作业
创设情境
归纳
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
应用新知
探究新知
1.对应点到旋转中心的距离相等.
旋转的性质
A
B
C
A′
B′
C′
O
巩固新知
课堂小结
布置作业
归纳
创设情境
轴对称
平移
形状
大小
方向
旋转
不变
不变
不变
不变
不变
不变
改变
不变
改变
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
操作
如图,已知点A和点A外一点O,你能画出点A绕点O顺时针旋转100°后的对应点B吗?
O
A
100°
B
M
旋转中心:点O
旋转方向:顺时针
旋转角度:100°
画法:
连接AO,在A点的右侧∠AOM=100°,在OM上截取OB=OA,则点B即为所求.
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
操作
已知:如下图,四边形ABCD和四边形外一点O,你能画出四边形ABCD绕点O顺时针旋转60°后的对应四边形A′B′C′D′吗?
O
A
B
C
D
旋转中心:点O
旋转方向:顺时针
旋转角度:60°
画法:
连接AO、 BO 、 CO 、 DO,分别做出四条线段旋转后的线段A′O、 B′O 、 C′O 、 D′O,顺次连接A′B′C′D′,即四边形A′B′C′D′为所求.
A′
D′
C′
B′
做一做
应用新知
探究新知
巩固新知
课堂小结
布置作业
归纳
创设情境
旋转作图关键步骤:
1. 确定旋转的三要素:旋转中心、旋转方向、旋转角.
2. 连接图形关键点与旋转中心后,分别作出线段的旋转图形.
3. 顺次连接关键点旋转后的对应点,所成图形即为所求.
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
选择不同的旋转中心,不同的旋转角旋转同一个图形,会出现不同的效果呢.
应用新知
探究新知
观察
旋转中心不变,旋转角改变
α
β
O
O
旋转角不变,旋转中心改变
O1
O2
巩固新知
课堂小结
布置作业
归纳
创设情境
注意:
旋转中心、旋转角、旋转方向不同,得到的同一图形的旋转图形的位置不同,但都全等.
应用新知
探究新知
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
A
B
C
D
E
分析:
关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
因此,在CB的延长线上取点E',使BE'=DE,则△ABE'为旋转后的图形.
解:因为点A是旋转中心,所以它的对应点是它本身.
正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
设点E的对应点为点E′.因为旋转后的图形与旋转前的图形全等,所以∠ABE′=∠ADE=90°,BE'=DE.
E′
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
如下图所示的四个图形中,△ABC经过旋转之后,不能得到△A′B′C′ 的是( )
A
B
C
A′
B′
C′
A.
A
B
C
A′
B′
C′
B.
A′
A
B
B′
C(C′)
A
B
C
A′
B′
C′
C.
D.
D
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B恰好落在边A′B′上,已知AB=4 cm,BB′=1 cm,则A′B的长度是( ) cm
A. 1
B.2
C.3
D.4
O
A
B
B′
A′
C
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫做格点).画出△ABC绕点O逆时针旋转90°后的△A′B′C′.
A
B
C
O
A′
B′
C′
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
图形的旋转
1. 确定旋转的三要素:旋转中心、旋转方向、旋转角.
2. 连接图形关键点与旋转中心后,分别作出线段的旋转图形.
3. 顺次连接关键点旋转后的对应点,所成图形即为所求.
旋转作图关键步骤
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
1.对应点到旋转中心的距离相等.
旋转的性质
布置作业
教科书第62页
习题1、2、3、4、5.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
23.1 图形的旋转
第2课时
学习目标
1.理解旋转的性质,了解旋转作图的步骤和关键.
2.能够根据旋转的性质作出常见图形的旋转图形.
3.通过观察、操作、交流、归纳等过程,培养学生探究问题的能力,动手能力和观察能力.
4. 经历探索旋转作图的过程,使学生充分感知数学美,培养学生学习数学的兴趣和热爱生活的情感.
图形的旋转
巩固新知
课堂小结
布置作业
轴对称
平移
形状
大小
方向
旋转
不变
不变
不变
不变
改变
不变
应用新知
创设情境
探究新知
回顾旧知
应用新知
巩固新知
课堂小结
布置作业
探究
在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸.先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A'BC'),移开硬纸板.△A'B'C'是由△ABC绕点O旋转得到的.
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
A
B
C
A′
B′
C′
线段OA与OA'有什么关系?∠AOA'与∠BOB'有什么关系?△ABC与△A'BC'的形状和大小有什么关系
O
点A与点A'是对应点
OA=OA'
点B与点B'是对应点
点C与点C'是对应点
量一量
OB=OB'
OC=OC'
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
A
B
C
A′
B′
C′
线段OA与OA'有什么关系?∠AOA'与∠BOB'有什么关系?△ABC与△A'BC'的形状和大小有什么关系
O
对应点到旋转中心的距离相等
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
A
B
C
A′
B′
C′
线段OA与OA'有什么关系?∠AOA'与∠BOB'有什么关系?△ABC与△A'BC'的形状和大小有什么关系
O
∠AOA'=∠BOB'
对应点与旋转中心所连线段的夹角都等于旋转角
量一量∠AOA'=∠COC'?
创设情境
探究新知
=∠COC'
应用新知
巩固新知
课堂小结
布置作业
探究
A
B
C
A′
B′
C′
线段OA与OA'有什么关系?∠AOA'与∠BOB'有什么关系?△ABC与△A'BC'的形状和大小有什么关系
O
旋转前、后的图形全等
创设情境
探究新知
巩固新知
课堂小结
布置作业
创设情境
归纳
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
应用新知
探究新知
1.对应点到旋转中心的距离相等.
旋转的性质
A
B
C
A′
B′
C′
O
巩固新知
课堂小结
布置作业
归纳
创设情境
轴对称
平移
形状
大小
方向
旋转
不变
不变
不变
不变
不变
不变
改变
不变
改变
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
操作
如图,已知点A和点A外一点O,你能画出点A绕点O顺时针旋转100°后的对应点B吗?
O
A
100°
B
M
旋转中心:点O
旋转方向:顺时针
旋转角度:100°
画法:
连接AO,在A点的右侧∠AOM=100°,在OM上截取OB=OA,则点B即为所求.
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
操作
已知:如下图,四边形ABCD和四边形外一点O,你能画出四边形ABCD绕点O顺时针旋转60°后的对应四边形A′B′C′D′吗?
O
A
B
C
D
旋转中心:点O
旋转方向:顺时针
旋转角度:60°
画法:
连接AO、 BO 、 CO 、 DO,分别做出四条线段旋转后的线段A′O、 B′O 、 C′O 、 D′O,顺次连接A′B′C′D′,即四边形A′B′C′D′为所求.
A′
D′
C′
B′
做一做
应用新知
探究新知
巩固新知
课堂小结
布置作业
归纳
创设情境
旋转作图关键步骤:
1. 确定旋转的三要素:旋转中心、旋转方向、旋转角.
2. 连接图形关键点与旋转中心后,分别作出线段的旋转图形.
3. 顺次连接关键点旋转后的对应点,所成图形即为所求.
应用新知
探究新知
巩固新知
课堂小结
布置作业
创设情境
选择不同的旋转中心,不同的旋转角旋转同一个图形,会出现不同的效果呢.
应用新知
探究新知
观察
旋转中心不变,旋转角改变
α
β
O
O
旋转角不变,旋转中心改变
O1
O2
巩固新知
课堂小结
布置作业
归纳
创设情境
注意:
旋转中心、旋转角、旋转方向不同,得到的同一图形的旋转图形的位置不同,但都全等.
应用新知
探究新知
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
A
B
C
D
E
分析:
关键是确定△ADE三个顶点的对应点,即它们旋转后的位置.
因此,在CB的延长线上取点E',使BE'=DE,则△ABE'为旋转后的图形.
解:因为点A是旋转中心,所以它的对应点是它本身.
正方形ABCD中,AD=AB,∠DAB=90°,所以旋转后点D与点B重合.
设点E的对应点为点E′.因为旋转后的图形与旋转前的图形全等,所以∠ABE′=∠ADE=90°,BE'=DE.
E′
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
如下图所示的四个图形中,△ABC经过旋转之后,不能得到△A′B′C′ 的是( )
A
B
C
A′
B′
C′
A.
A
B
C
A′
B′
C′
B.
A′
A
B
B′
C(C′)
A
B
C
A′
B′
C′
C.
D.
D
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
如图,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B恰好落在边A′B′上,已知AB=4 cm,BB′=1 cm,则A′B的长度是( ) cm
A. 1
B.2
C.3
D.4
O
A
B
B′
A′
C
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫做格点).画出△ABC绕点O逆时针旋转90°后的△A′B′C′.
A
B
C
O
A′
B′
C′
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
图形的旋转
1. 确定旋转的三要素:旋转中心、旋转方向、旋转角.
2. 连接图形关键点与旋转中心后,分别作出线段的旋转图形.
3. 顺次连接关键点旋转后的对应点,所成图形即为所求.
旋转作图关键步骤
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
1.对应点到旋转中心的距离相等.
旋转的性质
布置作业
教科书第62页
习题1、2、3、4、5.
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
