2022-2023学年人教版九年级数学上册23.1图形的旋转 课件(共18张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册23.1图形的旋转 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 21:28:53 | ||
图片预览





文档简介
(共18张PPT)
23.1 图形的旋转
第1课时
学习目标
1.掌握旋转的有关概念,理解旋转变换也是图形的一种基本变换.
2.能够识别旋转现象,并且能够判断旋转中心、旋转角、以及对应点.
3.通过探索旋转中心、旋转角、对应点的过程,培养学生的观察能力.
4. 经历探索旋转现象,探索旋转中心、旋转角、对应点的过程,让学生感受到事物间的数学现象,以及大自然中无处不在的数学之美,使对数学产生兴趣.
图形的旋转
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察与思考
风车、风扇、钟表在做什么运动?
旋转
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察与思考
生活中还有哪些旋转运动?
应用新知
巩固新知
课堂小结
布置作业
思考
如图,钟表的指针在不停地转动,从3时到6时,时针转动了多少度?
90°
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
思考
如图,风车风轮的每个叶片在风的吹动下转动到新的位置,每个叶片旋转的度数一样吗?
一样
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
创设情境
探究新知
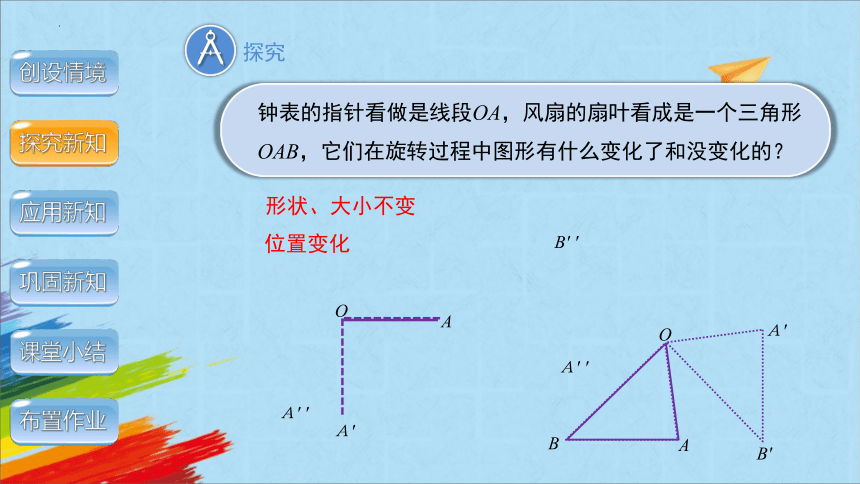
钟表的指针看做是线段OA,风扇的扇叶看成是一个三角形OAB,它们在旋转过程中图形有什么变化了和没变化的?
A
O
A
B
B′
A′
A′
A′ ′
A′ ′
B′ ′
形状、大小不变
位置变化
O
应用新知
巩固新知
课堂小结
布置作业
探究
创设情境
探究新知
钟表的指针看做是线段OA,风扇的扇叶看成是一个三角形OAB,它们在旋转过程中位置的变化有什么共同点?
O
A
O
A
B
B′
A′
A′
A′ ′
A′ ′
B′ ′
绕着一个点旋转
几何图形中每条线段旋转的角度一样
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
归纳
O
B
P
B ′
点O叫做旋转中心,转动的角叫做旋转角.
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点.
P ′
旋转中心
旋转角
P的对应点是P′
B的对应点是B′
O的对应点是O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
旋转的三要素:旋转中心、旋转角、旋转方向.
O
O
A
B
A
B
A′
B′
A′
B′
旋转中心
旋转中心
旋转角90°
逆时针
60°
旋转角60°
顺时针
巩固新知
课堂小结
布置作业
创设情境
归纳
1. 图形的旋转是图形绕着一点旋转一定的角度,即一定有旋转三要素.
5.旋转中心可以在图形内部、外部和图形上.
O
A
B
A′
B′
60°
旋转中心
顺时针
6.旋转角由旋转前后对应点与旋转中心连线构成的角度.
应用新知
探究新知
2.旋转的范围是平面内的旋转.
3.旋转前后图形重合(判断旋转的关键).
4.旋转中心是点而不是线段,旋转必须指出旋转方向.
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,△OAB绕点O按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
O
E
F
B
A
(1)旋转中心是点O,
∠AOE, ∠BOF是旋转角.
(2)经过旋转,点A、B分别移动
到点E、F位置.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
下列运动属于旋转的是 ( )
A. 篮球的滚动
B.钟表上钟摆的摆动
C.气球垂直升空的运动
D.一个图形沿某直线对折的过程
B
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
如图,能由左边的图形旋转得到的右边图形是 ( )
A.
B.
C.
D.
B
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意得是 ( )
B
A.顺时针旋转90°
B.逆时针旋转90°
C.顺时针旋转45°
D.逆时针旋转45°
B
C
A
E
D
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
图形的旋转
1. 图形的旋转是图形绕着一点旋转一定的角度,即一定有旋转三要素.
5.旋转中心可以在图形内部、外部和图形上.
6.旋转角由旋转前后对应点与旋转中心连线构成的角度.
2. 旋转前后图形重合(判断旋转的关键).
3. 旋转中心是点而不是线段,旋转必须指出旋转方向.
4. 旋转的范围是平面内的旋转.
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
点O叫做旋转中心,转动的角叫做旋转角.
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的
对应点.
布置作业
教科书第59页练习1、2、3
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
23.1 图形的旋转
第1课时
学习目标
1.掌握旋转的有关概念,理解旋转变换也是图形的一种基本变换.
2.能够识别旋转现象,并且能够判断旋转中心、旋转角、以及对应点.
3.通过探索旋转中心、旋转角、对应点的过程,培养学生的观察能力.
4. 经历探索旋转现象,探索旋转中心、旋转角、对应点的过程,让学生感受到事物间的数学现象,以及大自然中无处不在的数学之美,使对数学产生兴趣.
图形的旋转
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察与思考
风车、风扇、钟表在做什么运动?
旋转
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
观察与思考
生活中还有哪些旋转运动?
应用新知
巩固新知
课堂小结
布置作业
思考
如图,钟表的指针在不停地转动,从3时到6时,时针转动了多少度?
90°
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
思考
如图,风车风轮的每个叶片在风的吹动下转动到新的位置,每个叶片旋转的度数一样吗?
一样
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
创设情境
探究新知
钟表的指针看做是线段OA,风扇的扇叶看成是一个三角形OAB,它们在旋转过程中图形有什么变化了和没变化的?
A
O
A
B
B′
A′
A′
A′ ′
A′ ′
B′ ′
形状、大小不变
位置变化
O
应用新知
巩固新知
课堂小结
布置作业
探究
创设情境
探究新知
钟表的指针看做是线段OA,风扇的扇叶看成是一个三角形OAB,它们在旋转过程中位置的变化有什么共同点?
O
A
O
A
B
B′
A′
A′
A′ ′
A′ ′
B′ ′
绕着一个点旋转
几何图形中每条线段旋转的角度一样
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
归纳
O
B
P
B ′
点O叫做旋转中心,转动的角叫做旋转角.
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点.
P ′
旋转中心
旋转角
P的对应点是P′
B的对应点是B′
O的对应点是O
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
旋转的三要素:旋转中心、旋转角、旋转方向.
O
O
A
B
A
B
A′
B′
A′
B′
旋转中心
旋转中心
旋转角90°
逆时针
60°
旋转角60°
顺时针
巩固新知
课堂小结
布置作业
创设情境
归纳
1. 图形的旋转是图形绕着一点旋转一定的角度,即一定有旋转三要素.
5.旋转中心可以在图形内部、外部和图形上.
O
A
B
A′
B′
60°
旋转中心
顺时针
6.旋转角由旋转前后对应点与旋转中心连线构成的角度.
应用新知
探究新知
2.旋转的范围是平面内的旋转.
3.旋转前后图形重合(判断旋转的关键).
4.旋转中心是点而不是线段,旋转必须指出旋转方向.
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,△OAB绕点O按顺时针方向旋转得到△OEF,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?
(2)经过旋转,点A、B分别移动到什么位置?
O
E
F
B
A
(1)旋转中心是点O,
∠AOE, ∠BOF是旋转角.
(2)经过旋转,点A、B分别移动
到点E、F位置.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
下列运动属于旋转的是 ( )
A. 篮球的滚动
B.钟表上钟摆的摆动
C.气球垂直升空的运动
D.一个图形沿某直线对折的过程
B
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
如图,能由左边的图形旋转得到的右边图形是 ( )
A.
B.
C.
D.
B
应用新知
课堂小结
布置作业
创设情境
练习3
随堂练习
探究新知
巩固新知
如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意得是 ( )
B
A.顺时针旋转90°
B.逆时针旋转90°
C.顺时针旋转45°
D.逆时针旋转45°
B
C
A
E
D
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
图形的旋转
1. 图形的旋转是图形绕着一点旋转一定的角度,即一定有旋转三要素.
5.旋转中心可以在图形内部、外部和图形上.
6.旋转角由旋转前后对应点与旋转中心连线构成的角度.
2. 旋转前后图形重合(判断旋转的关键).
3. 旋转中心是点而不是线段,旋转必须指出旋转方向.
4. 旋转的范围是平面内的旋转.
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
点O叫做旋转中心,转动的角叫做旋转角.
如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的
对应点.
布置作业
教科书第59页练习1、2、3
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
