5.2.1三角函数的概念 课件(共35张PPT)
文档属性
| 名称 | 5.2.1三角函数的概念 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 16:57:45 | ||
图片预览










文档简介
(共35张PPT)
5.2 三角函数的概念
5.2.1 三角函数的概念
明确目标 发展素养
1.借助单位圆理解任意角三角函数 (正弦、余弦、正切)的定义. 2.掌握任意角三角函数(正弦、余弦、正切)在各象限的符号. 3.掌握诱导公式一并会应用. 1.通过三角函数的概念,培养数学抽象素养.
2.借助公式的运算,提升数学运算素养.
知识点一 三角函数的定义
(一)教材梳理填空
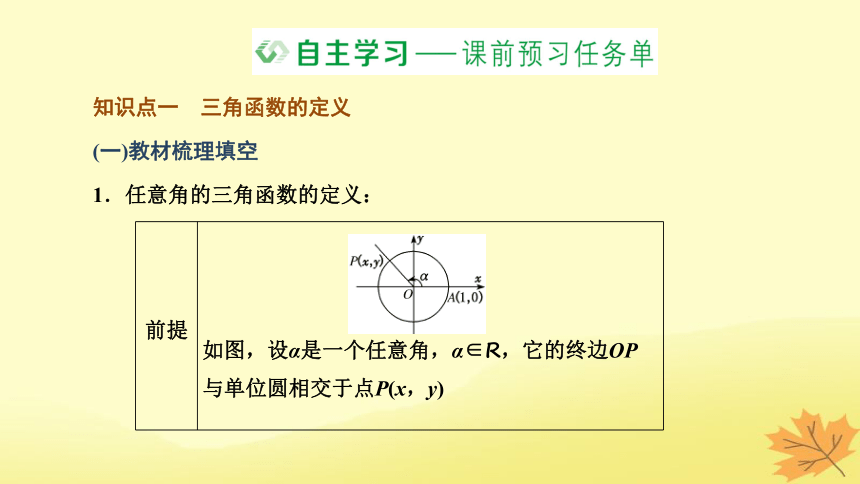
1.任意角的三角函数的定义:
前提
如图,设α是一个任意角,α∈R,它的终边OP与单位圆相交于点P(x,y)
续表
y
sin α
x
cos α
tan α(x≠0)
三角函数 正弦、余弦、正切都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,将它们统称为三角函数
续表
[微思考] 三角函数值的大小与点P在角α终边上位置是否有关?
提示:三角函数值是比值,是一个实数,它的大小与点P在角α终边上的位置无关,只与角α的终边位置有关,即三角函数值的大小只与角有关.
2.正弦、余弦、正切函数在弧度制下的定义域:
三角函数 定义域
sin α R
cos α R
tan α
_____________________
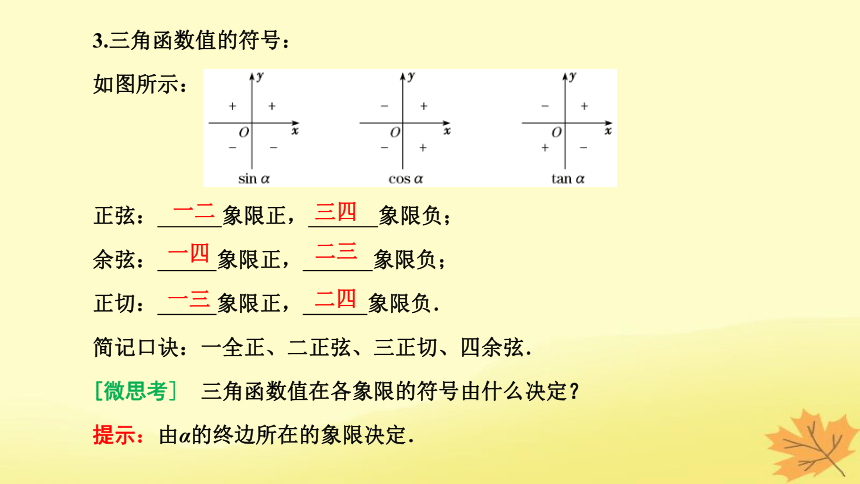
3.三角函数值的符号:
如图所示:
正弦: 象限正, 象限负;
余弦: 象限正, 象限负;
正切: 象限正, 象限负.
简记口诀:一全正、二正弦、三正切、四余弦.
[微思考] 三角函数值在各象限的符号由什么决定?
提示:由α的终边所在的象限决定.
一二
三四
一四
二三
一三
二四
(二)基本知能小试
1.判断正误
(1)已知α是三角形的内角,则必有sin α>0. ( )
(2)若sin α>0,则α是第一或第二象限角. ( )
(3)对于任意角α,sin α,cos α,tan α都有意义. ( )
答案:(1)√ (2)× (3)×
2.若sin α<0,tan α>0,则α在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:由sin α<0可知α在第三或第四象限,由tan α>0可知α在第一或第三象限,综上,α在第三象限.
答案:C
答案:B
知识点二 诱导公式一
(一)教材梳理填空
(1)终边相同的角的同一三角函数的值 ______.
(2)公式
[微思考] 同一三角函数值相等时,角是否一定相等或相差周角的整数倍?
相等
(二)基本知能小试
1.判断正误
(1)若α=β+720°,则cos α=cos β. ( )
(2)若sin α=sin β,则α=β. ( )
答案:(1)√ (2)×
答案:C
题型一 三角函数的定义与应用
[探究发现]
(1)一般地,设角α终边上任意一点的坐标为(x,y),它与原点的距离为r,则sin α,cos α,tan α为何值?
(2)对于一个任意给定的角α,按照上述定义,对应的sin α,cos α,tan α的值是否存在?是否唯一?
提示:角α的终边在y轴上时,tan α的值无意义,除此之外,其他的角的三角函数值都是唯一确定的.
(3)若已知α终边所在的直线方程为y=kx,则如何求sin α,cos α,tan α的值.
【对点练清】
1.若本例(2)中的条件变为“已知角α的终边落在直线y=2x上”,求sin α,cos α,tan α的值.
2.已知角α的终边过点P(-3a,4a)(a≠0),求2sin α+cos α.
[典例2] (1)已知点P(sin θ,sin θcos θ)位于第二象限,那么角θ所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
(2)判断下列各式的符号:
①sin 2 020°cos 2 021°tan 2 022°;
②tan 191°-cos 191°;
③sin 2cos 3tan 4.
[解析] (1)由点P(sin θ,sin θcos θ)位于第二象限,
可得sin θ<0,sin θcos θ>0,可得sin θ<0,cos θ<0,
所以角θ所在的象限是第三象限.
[方法技巧]
有关三角函数值符号问题的解题策略
(1)已知角α的三角函数值(sin α,cos α,tan α)中任意两个的符号,可分别确定出角α终边所在的可能位置,二者的公共部分即角α的终边位置.注意终边在坐标轴上的特殊情况.
(2)对于多个三角函数值符号的判断问题,要进行分类讨论.
(3)对于确定角α是第几象限角的问题,应先确定题目中所有三角函数值的符号,然后依据上述三角函数值的符号来确定角α是第几象限角,它们的公共部分即为所求;对于已知角α的终边所在的象限来判断角α的三角函数值的符号问题,则常依据三角函数的定义,或利用口诀“一全正、二正弦、三正切、四余弦”来解决.
【对点练清】
1.若三角形的两内角α,β满足sin α·cos β<0,则此三角形必为 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.以上三种情况都有可能
解析:三角形的两内角α,β的终边一定落在第一、二象限或y轴正半轴上,sin α·cos β<0,所以sin α>0,cos β<0,所以角β为钝角,此三角形为钝角三角形.
答案:B
题型三 诱导公式一的应用
【学透用活】
对诱导公式一的三点说明
(1)公式一的实质是终边相同的角的三角函数值相等.
(2)公式一的结构特征:
①左、右为同一三角函数;
②公式左边的角为α+k·2π,右边的角为α.
注意公式一中的条件k∈Z不可遗漏.
(3)公式一的作用:把求任意角的三角函数值转化为求0~2π(或0°~360°)范围内的角的三角函数值.
[方法技巧] 利用诱导公式一进行化简求值的步骤
提示:错误.错误的根本原因是忽视对点的坐标中的参数进行分类讨论.实际上本题中要分x=0和x≠0两种情况讨论.
二、应用性——强调学以致用
2.[好题共享——选自人教B版新教材]将如图(1)所示的摩天轮抽象成如图(2)所示的平面图形,然后以摩天轮转轮中心为原点,以水平线为x轴,建立平面直角坐标系.设O到地面的高OT为l m,点P为转轮上任意一点,转轮半径OP为r m.记以OP为终边的角为α rad,点P离地面的高度为h m,试用l,r与α表示h.
[析题建模]
解:过点P作x轴的垂线,垂足为M,则:
当α的终边在第一、二象限或y轴正半轴上时,
h=OT+MP=l+rsin α;
当α的终边在第三、四象限或y轴负半轴上时,
因为MP=-rsin α,此时h=OT-MP=l+rsin α;
当α的终边在x轴上时,sin α=0,此时h=OT=l+rsin α.
所以,不管α的终边在何处,都有h=l+rsin α.
5.2 三角函数的概念
5.2.1 三角函数的概念
明确目标 发展素养
1.借助单位圆理解任意角三角函数 (正弦、余弦、正切)的定义. 2.掌握任意角三角函数(正弦、余弦、正切)在各象限的符号. 3.掌握诱导公式一并会应用. 1.通过三角函数的概念,培养数学抽象素养.
2.借助公式的运算,提升数学运算素养.
知识点一 三角函数的定义
(一)教材梳理填空
1.任意角的三角函数的定义:
前提
如图,设α是一个任意角,α∈R,它的终边OP与单位圆相交于点P(x,y)
续表
y
sin α
x
cos α
tan α(x≠0)
三角函数 正弦、余弦、正切都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,将它们统称为三角函数
续表
[微思考] 三角函数值的大小与点P在角α终边上位置是否有关?
提示:三角函数值是比值,是一个实数,它的大小与点P在角α终边上的位置无关,只与角α的终边位置有关,即三角函数值的大小只与角有关.
2.正弦、余弦、正切函数在弧度制下的定义域:
三角函数 定义域
sin α R
cos α R
tan α
_____________________
3.三角函数值的符号:
如图所示:
正弦: 象限正, 象限负;
余弦: 象限正, 象限负;
正切: 象限正, 象限负.
简记口诀:一全正、二正弦、三正切、四余弦.
[微思考] 三角函数值在各象限的符号由什么决定?
提示:由α的终边所在的象限决定.
一二
三四
一四
二三
一三
二四
(二)基本知能小试
1.判断正误
(1)已知α是三角形的内角,则必有sin α>0. ( )
(2)若sin α>0,则α是第一或第二象限角. ( )
(3)对于任意角α,sin α,cos α,tan α都有意义. ( )
答案:(1)√ (2)× (3)×
2.若sin α<0,tan α>0,则α在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:由sin α<0可知α在第三或第四象限,由tan α>0可知α在第一或第三象限,综上,α在第三象限.
答案:C
答案:B
知识点二 诱导公式一
(一)教材梳理填空
(1)终边相同的角的同一三角函数的值 ______.
(2)公式
[微思考] 同一三角函数值相等时,角是否一定相等或相差周角的整数倍?
相等
(二)基本知能小试
1.判断正误
(1)若α=β+720°,则cos α=cos β. ( )
(2)若sin α=sin β,则α=β. ( )
答案:(1)√ (2)×
答案:C
题型一 三角函数的定义与应用
[探究发现]
(1)一般地,设角α终边上任意一点的坐标为(x,y),它与原点的距离为r,则sin α,cos α,tan α为何值?
(2)对于一个任意给定的角α,按照上述定义,对应的sin α,cos α,tan α的值是否存在?是否唯一?
提示:角α的终边在y轴上时,tan α的值无意义,除此之外,其他的角的三角函数值都是唯一确定的.
(3)若已知α终边所在的直线方程为y=kx,则如何求sin α,cos α,tan α的值.
【对点练清】
1.若本例(2)中的条件变为“已知角α的终边落在直线y=2x上”,求sin α,cos α,tan α的值.
2.已知角α的终边过点P(-3a,4a)(a≠0),求2sin α+cos α.
[典例2] (1)已知点P(sin θ,sin θcos θ)位于第二象限,那么角θ所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
(2)判断下列各式的符号:
①sin 2 020°cos 2 021°tan 2 022°;
②tan 191°-cos 191°;
③sin 2cos 3tan 4.
[解析] (1)由点P(sin θ,sin θcos θ)位于第二象限,
可得sin θ<0,sin θcos θ>0,可得sin θ<0,cos θ<0,
所以角θ所在的象限是第三象限.
[方法技巧]
有关三角函数值符号问题的解题策略
(1)已知角α的三角函数值(sin α,cos α,tan α)中任意两个的符号,可分别确定出角α终边所在的可能位置,二者的公共部分即角α的终边位置.注意终边在坐标轴上的特殊情况.
(2)对于多个三角函数值符号的判断问题,要进行分类讨论.
(3)对于确定角α是第几象限角的问题,应先确定题目中所有三角函数值的符号,然后依据上述三角函数值的符号来确定角α是第几象限角,它们的公共部分即为所求;对于已知角α的终边所在的象限来判断角α的三角函数值的符号问题,则常依据三角函数的定义,或利用口诀“一全正、二正弦、三正切、四余弦”来解决.
【对点练清】
1.若三角形的两内角α,β满足sin α·cos β<0,则此三角形必为 ( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.以上三种情况都有可能
解析:三角形的两内角α,β的终边一定落在第一、二象限或y轴正半轴上,sin α·cos β<0,所以sin α>0,cos β<0,所以角β为钝角,此三角形为钝角三角形.
答案:B
题型三 诱导公式一的应用
【学透用活】
对诱导公式一的三点说明
(1)公式一的实质是终边相同的角的三角函数值相等.
(2)公式一的结构特征:
①左、右为同一三角函数;
②公式左边的角为α+k·2π,右边的角为α.
注意公式一中的条件k∈Z不可遗漏.
(3)公式一的作用:把求任意角的三角函数值转化为求0~2π(或0°~360°)范围内的角的三角函数值.
[方法技巧] 利用诱导公式一进行化简求值的步骤
提示:错误.错误的根本原因是忽视对点的坐标中的参数进行分类讨论.实际上本题中要分x=0和x≠0两种情况讨论.
二、应用性——强调学以致用
2.[好题共享——选自人教B版新教材]将如图(1)所示的摩天轮抽象成如图(2)所示的平面图形,然后以摩天轮转轮中心为原点,以水平线为x轴,建立平面直角坐标系.设O到地面的高OT为l m,点P为转轮上任意一点,转轮半径OP为r m.记以OP为终边的角为α rad,点P离地面的高度为h m,试用l,r与α表示h.
[析题建模]
解:过点P作x轴的垂线,垂足为M,则:
当α的终边在第一、二象限或y轴正半轴上时,
h=OT+MP=l+rsin α;
当α的终边在第三、四象限或y轴负半轴上时,
因为MP=-rsin α,此时h=OT-MP=l+rsin α;
当α的终边在x轴上时,sin α=0,此时h=OT=l+rsin α.
所以,不管α的终边在何处,都有h=l+rsin α.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
