2022-2023学年人教版九年级数学上册 22.3 实际问题与二次函数(第3课时)课件(共18张PPT)
文档属性
| 名称 | 2022-2023学年人教版九年级数学上册 22.3 实际问题与二次函数(第3课时)课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 06:39:52 | ||
图片预览



文档简介
(共18张PPT)
22.3 实际问题与二次函数
第3课时
学习目标
1.能根据具体几何问题建立合适的直角坐标系,找出数量关系;
2.能建立二次函数解析式,并能应用二次函数的相关性质解决实际几何问题;
3.从“数”(解析式)和“形”(图象)的角度理解二次函数与实际问题之间的联系,体会“数形结合”的思想,以及建模的转化思想;
4. 经历了建模来解决实际生活中的问题,体会函数知识的实际应用价值,感受数学与人类生活的密切联系.
建系解决实际问题
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
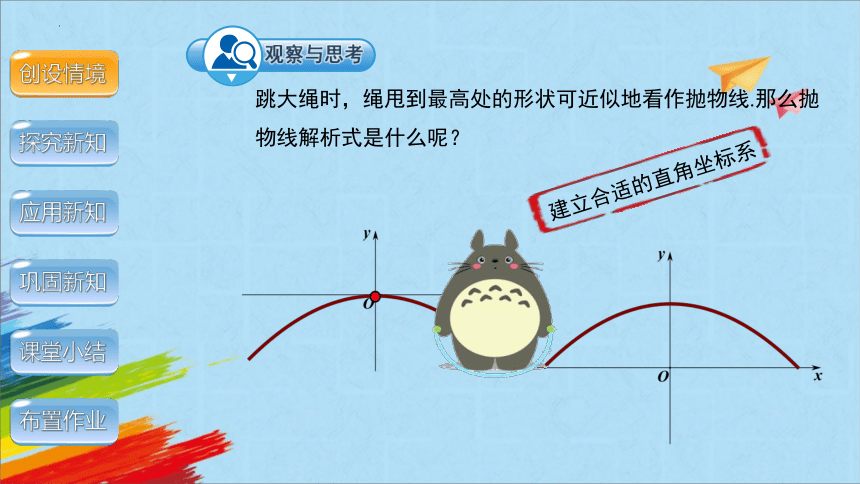
跳大绳时,绳甩到最高处的形状可近似地看作抛物线.那么抛物线解析式是什么呢?
观察与思考
建立合适的直角坐标系
应用新知
巩固新知
课堂小结
布置作业
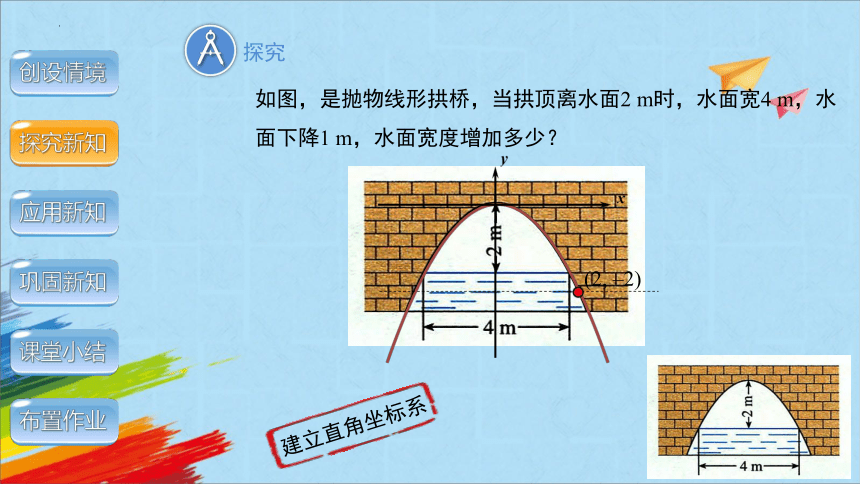
探究
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m,水面宽度增加多少?
(2, –2)
建立直角坐标系
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m,水面宽度增加多少?
(2,–2)
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
设抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,–2),可得
– 2=a×22,
这条抛物线表示的二次函数为
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
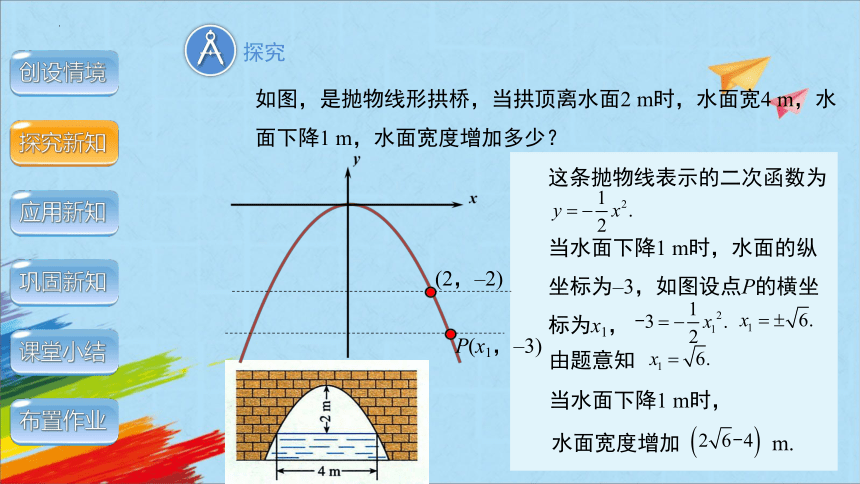
探究
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m,水面宽度增加多少?
(2,–2)
这条抛物线表示的二次函数为
当水面下降1 m时,水面的纵坐标为–3,如图设点P的横坐标为x1,
P(x1,–3)
由题意知
水面宽度增加 m.
创设情境
探究新知
当水面下降1 m时,
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
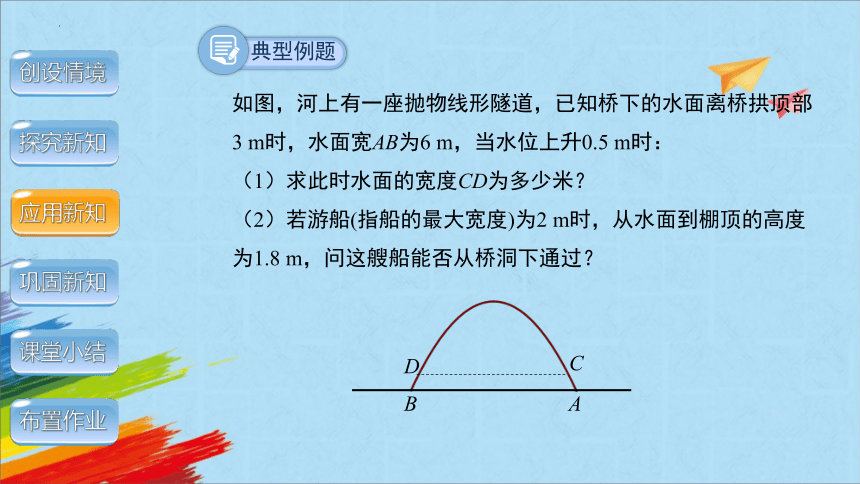
如图,河上有一座抛物线形隧道,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
(2)若游船(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
C
D
A
B
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,河上有一座抛物线形隧道,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
C
D
A
B
解:(1)建立如图所示的直角坐标系,
则点E(0,3),A(3,0),B(– 3,0)
设抛物线的解析式为y=ax2+k.
把点E,点A坐标代入到抛物线的解析式中.
E
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,河上有一座抛物线形隧道,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
当y=0.5时,
故水面宽度CD= m.
C
D
A
B
E
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,河上有一座抛物线形隧道,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(2)若游船(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
(2)当x=1时,
所以这艘游船能通过.
C
D
E
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
建立二次函数模型解决建筑类实际问题的一般步骤:
① 根据题意建立适当的平面直角坐标系.
② 把已知条件转化为点的坐标.
③ 合理设出函数的解析式.
④ 利用待定系数法求出函数解析式.
⑤ 利用求得的关系式进一步分析,并进行有关的判断.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
有一拱桥洞呈抛物线形,这个桥洞的最大高度是16 m,跨度为40 m,现把它的示意图放在坐标系中,则抛物线的解析式为( )
A.
B.
C.
D.
C
某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高各有一个壁灯,两壁灯之间的水平距离为6 m,如图所示,则厂门的高为(水泥建筑物厚度忽略不计,精确到0.1 m) ( )
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
A. 6.9 m B. 7.0 m C. 7.1 m D. 6.8 m
A
课堂小结
布置作业
探究新知
创设情境
应用新知
巩固新知
练习3
随堂练习
如图,小明的父亲在相距2 m的两棵树间拴了一根绳子,给小明做了一个简易的秋千,拴绳子的地方A、B距地面高都是2.5 m,绳子自然下垂呈抛物线状,身高1 m的小明距较近的那棵树0.5 m时,头部刚好接触到绳子C处,求绳子的最低点距地面的距离.
A
B
C
课堂小结
布置作业
探究新知
创设情境
应用新知
巩固新知
随堂练习
解:建立如右图所示的直角坐标系.这时绳子所成抛物线的对称轴是y轴,所以可设它的函数解析式为y=ax2+k.
所以抛物线的解析式为y=2x2+0.5.
因为a=2>0,所以y有最小值,即当x=0时,
y最小值=0.5.
即绳子的最低点距地面的距离0.5 m.
由题意知B(1,2.5),C(– 0.5,1)在抛物线上,
A
B
C
y
x
O
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
建系解决实际问题
建立二次函数模型解决建筑类实际问题的一般步骤:
① 根据题意建立适当的平面直角坐标系.
②把已知条件转化为点的坐标.
③合理设出函数的解析式.
④利用待定系数法求出函数解析式.
⑤利用求得的关系式进一步分析,并进行有关的判断.
布置作业
教科书第56页复习题22
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
22.3 实际问题与二次函数
第3课时
学习目标
1.能根据具体几何问题建立合适的直角坐标系,找出数量关系;
2.能建立二次函数解析式,并能应用二次函数的相关性质解决实际几何问题;
3.从“数”(解析式)和“形”(图象)的角度理解二次函数与实际问题之间的联系,体会“数形结合”的思想,以及建模的转化思想;
4. 经历了建模来解决实际生活中的问题,体会函数知识的实际应用价值,感受数学与人类生活的密切联系.
建系解决实际问题
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
跳大绳时,绳甩到最高处的形状可近似地看作抛物线.那么抛物线解析式是什么呢?
观察与思考
建立合适的直角坐标系
应用新知
巩固新知
课堂小结
布置作业
探究
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m,水面宽度增加多少?
(2, –2)
建立直角坐标系
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m,水面宽度增加多少?
(2,–2)
以抛物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系.
设抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,–2),可得
– 2=a×22,
这条抛物线表示的二次函数为
创设情境
探究新知
应用新知
巩固新知
课堂小结
布置作业
探究
如图,是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m,水面下降1 m,水面宽度增加多少?
(2,–2)
这条抛物线表示的二次函数为
当水面下降1 m时,水面的纵坐标为–3,如图设点P的横坐标为x1,
P(x1,–3)
由题意知
水面宽度增加 m.
创设情境
探究新知
当水面下降1 m时,
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,河上有一座抛物线形隧道,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
(2)若游船(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
C
D
A
B
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,河上有一座抛物线形隧道,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
C
D
A
B
解:(1)建立如图所示的直角坐标系,
则点E(0,3),A(3,0),B(– 3,0)
设抛物线的解析式为y=ax2+k.
把点E,点A坐标代入到抛物线的解析式中.
E
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,河上有一座抛物线形隧道,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(1)求此时水面的宽度CD为多少米?
当y=0.5时,
故水面宽度CD= m.
C
D
A
B
E
巩固新知
课堂小结
布置作业
探究新知
典型例题
创设情境
应用新知
如图,河上有一座抛物线形隧道,已知桥下的水面离桥拱顶部3 m时,水面宽AB为6 m,当水位上升0.5 m时:
(2)若游船(指船的最大宽度)为2 m时,从水面到棚顶的高度为1.8 m,问这艘船能否从桥洞下通过?
(2)当x=1时,
所以这艘游船能通过.
C
D
E
应用新知
巩固新知
课堂小结
布置作业
创设情境
探究新知
归纳
建立二次函数模型解决建筑类实际问题的一般步骤:
① 根据题意建立适当的平面直角坐标系.
② 把已知条件转化为点的坐标.
③ 合理设出函数的解析式.
④ 利用待定系数法求出函数解析式.
⑤ 利用求得的关系式进一步分析,并进行有关的判断.
应用新知
课堂小结
布置作业
创设情境
练习1
随堂练习
探究新知
巩固新知
有一拱桥洞呈抛物线形,这个桥洞的最大高度是16 m,跨度为40 m,现把它的示意图放在坐标系中,则抛物线的解析式为( )
A.
B.
C.
D.
C
某工厂的大门是一抛物线形水泥建筑物,大门的地面宽度为8 m,两侧距地面3 m高各有一个壁灯,两壁灯之间的水平距离为6 m,如图所示,则厂门的高为(水泥建筑物厚度忽略不计,精确到0.1 m) ( )
应用新知
课堂小结
布置作业
创设情境
练习2
随堂练习
探究新知
巩固新知
A. 6.9 m B. 7.0 m C. 7.1 m D. 6.8 m
A
课堂小结
布置作业
探究新知
创设情境
应用新知
巩固新知
练习3
随堂练习
如图,小明的父亲在相距2 m的两棵树间拴了一根绳子,给小明做了一个简易的秋千,拴绳子的地方A、B距地面高都是2.5 m,绳子自然下垂呈抛物线状,身高1 m的小明距较近的那棵树0.5 m时,头部刚好接触到绳子C处,求绳子的最低点距地面的距离.
A
B
C
课堂小结
布置作业
探究新知
创设情境
应用新知
巩固新知
随堂练习
解:建立如右图所示的直角坐标系.这时绳子所成抛物线的对称轴是y轴,所以可设它的函数解析式为y=ax2+k.
所以抛物线的解析式为y=2x2+0.5.
因为a=2>0,所以y有最小值,即当x=0时,
y最小值=0.5.
即绳子的最低点距地面的距离0.5 m.
由题意知B(1,2.5),C(– 0.5,1)在抛物线上,
A
B
C
y
x
O
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
建系解决实际问题
建立二次函数模型解决建筑类实际问题的一般步骤:
① 根据题意建立适当的平面直角坐标系.
②把已知条件转化为点的坐标.
③合理设出函数的解析式.
④利用待定系数法求出函数解析式.
⑤利用求得的关系式进一步分析,并进行有关的判断.
布置作业
教科书第56页复习题22
探究新知
应用新知
课堂小结
巩固新知
创设情境
再见
同课章节目录
