5.1.2弧度制 课件(共35张PPT)
文档属性
| 名称 | 5.1.2弧度制 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 16:58:54 | ||
图片预览









文档简介
(共35张PPT)
5.1.2 弧度制
明确目标 发展素养
1.了解任意角的弧度制. 2.能进行弧度与角度的互化. 3.理解“1弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数. 4.了解角度制与弧度制的区别与联系. 1.通过对弧度制概念的学习,培养数学抽象素养.
2.借助弧度制与角度制的换算,提升数学运算素养.
知识点一 角度制与弧度制
(一)教材梳理填空
1.度量角的两种制度:
角度制 定义 用 为单位进行度量角的单位制
1度的角
1度的角等于周角的 ,记作1°
弧度制 定义 以 为单位来度量角的单位制
1弧度 的角 长度等于 的圆弧所对的圆心角叫做1弧度的角.
1弧度记作1 ____
度
弧度
半径长
rad
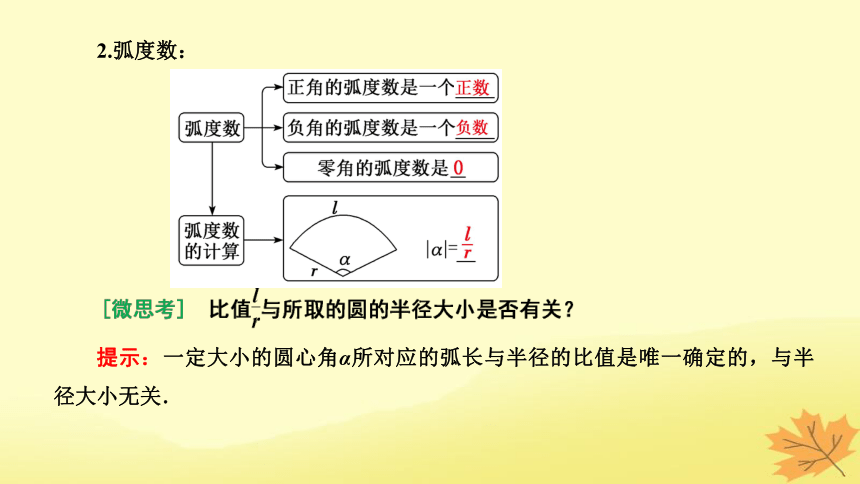
2.弧度数:
提示:一定大小的圆心角α所对应的弧长与半径的比值是唯一确定的,与半径大小无关.
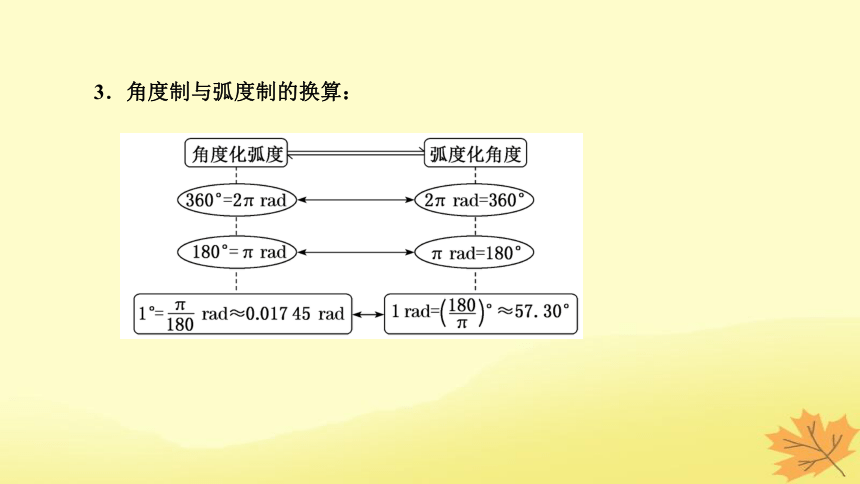
3.角度制与弧度制的换算:
4.角度制与弧度制的比较:
由于进位制不同,同一个角的弧度数与角度数一般是不同的.
[微思考] (1)半径不同的圆中,相同的圆心角所对的弧度数是否相同?
提示:相同.角的弧度数的大小与所在圆的半径的大小无关,只与圆心角的大小有关.
(2)2°与2弧度的角是否表示同一个角?
提示:不是同一个角.2°是角度制,2是弧度制,2 rad约为115°.
角度制 用度作为单位来度量角的单位制 单位“°”不能省略 角的正负与方向有关 六十进制
弧度制 用弧度作为单位来度量角的单位制 单位“rad”可以省略 角的正负与方向有关 十进制
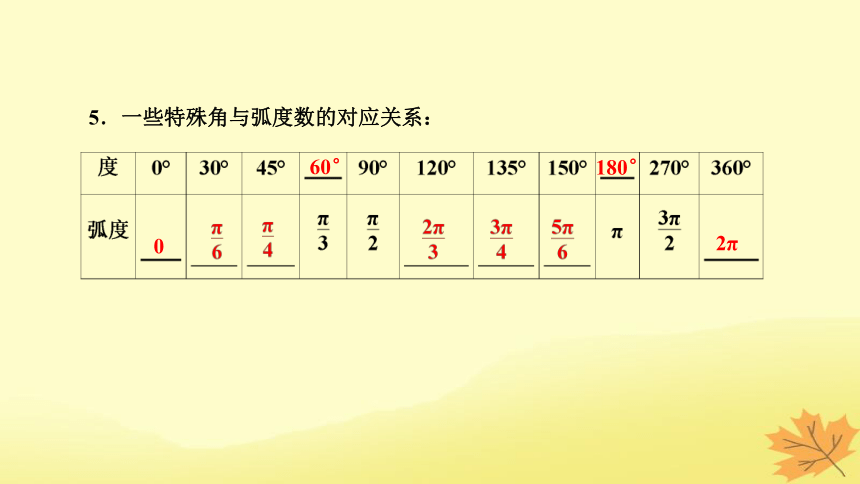
5.一些特殊角与弧度数的对应关系:
0
2π
60°
180°
答案:C
知识点二 扇形的弧长和面积公式
(一)教材梳理填空
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则
(1)弧长公式:l= .
(2)扇形面积公式:S= = .
αR
(二)基本知能小试
1.判断正误:
(1)扇形的半径为1 cm,圆心角为30°,则扇形的弧长l=r|α|=1×30=30(cm). ( )
(2)若扇形的半径不变,圆心角扩大为原来的2倍,则扇形的弧长也扩大为原来的2倍. ( )
(3)若扇形的半径和弧长都变为原来的2倍,则扇形的面积变为原来的2倍.( )
答案:(1)× (2)√ (3)×
题型一 角度与弧度的换算
【学透用活】
角与实数的对应
(1)角的概念推广后,无论是用角度制还是用弧度制,都能在角的集合与实数集R之间建立一种一一对应的关系:即每一个角都有唯一的一个实数(如这个角的度数或弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(如弧度数或角度数等于这个实数的角)与它对应.
(2)由于弧度制的单位与实数单位一致,所以能给研究问题带来方便.
题型二 用弧度制表示角有关的角
【学透用活】
[典例2] 已知角α=2 005°.
(1)将α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出α是第几象限的角;
(2)在[-5π,0)内找出与α终边相同的角.
[方法技巧]
1.弧度制下与角α终边相同的角的表示
在弧度制下,与角α的终边相同的角可以表示为{β|β=2kπ+α,k∈Z},即与角α终边相同的角可以表示成α加上2π的整数倍.
2.根据已知图形写出区域角的集合的步骤
(1)仔细观察图形.
(2)写出区域边界作为终边时角的表示.
(3)用不等式表示区域范围内的角.
3.用弧度表示角的注意点
(1)注意角度与弧度不能混用.
(2)各终边相同的角需加2kπ,k∈Z.
(3)求两个角的集合的交集时,注意应用数轴直观确定,可对k进行适当的赋值.
2. 用弧度制表示终边在图中阴影区域内角的集合(包括边界),
并判断2 012°是不是这个集合的元素.
提示:应注意结果是圆心角的绝对值,具体应用时既要注意其大小,又要注意其正负.
(2)在使用弧度制下的弧长公式及面积公式时,若已知的角是以“度”为单位,需注意什么问题?
提示:若已知的角是以“度”为单位,则必须先把它化成弧度后再计算,否则结果易出错.
【学透用活】
[典例3] 已知扇形的周长为10 cm,面积为4 cm2,求扇形圆心角的弧度数.
[方法技巧]
1.弧度制下有关扇形弧长、面积问题的解题策略
涉及扇形的周长、弧长、圆心角、面积等的计算,关键是先分析题目已知哪些量求哪些量,然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解.
2 .扇形弧长、面积公式的变形运用
3 .谨记3个注意点
(1)在弧度制中的弧长公式及扇形面积公式中的圆心角可正可负.
(2)看清角的度量制,选用相应的公式.
(3)扇形的周长等于弧长加两个半径长.
【对点练清】
1.已知一扇形的圆心角是72°,半径为20,求扇形的面积.
2.已知扇形的周长为20 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
二、应用性——强调学以致用
2.某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇
环的周长为30米,其中大圆弧所在圆的半径为10米.设小
圆弧所在圆的半径为x米,圆心角为θ(弧度).
(1)求θ关于x的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.
[析题建模] (1)利用扇形的弧长公式,结合扇环面的周长,可求θ关于x的函数关系式.
(2)分别求出花坛的面积、装饰总费用,可求y关于x的函数关系式,然后换元,利用基本不等式求最大值.
5.1.2 弧度制
明确目标 发展素养
1.了解任意角的弧度制. 2.能进行弧度与角度的互化. 3.理解“1弧度的角”的定义,掌握弧度与角度的换算、弧长公式和扇形面积公式,熟悉特殊角的弧度数. 4.了解角度制与弧度制的区别与联系. 1.通过对弧度制概念的学习,培养数学抽象素养.
2.借助弧度制与角度制的换算,提升数学运算素养.
知识点一 角度制与弧度制
(一)教材梳理填空
1.度量角的两种制度:
角度制 定义 用 为单位进行度量角的单位制
1度的角
1度的角等于周角的 ,记作1°
弧度制 定义 以 为单位来度量角的单位制
1弧度 的角 长度等于 的圆弧所对的圆心角叫做1弧度的角.
1弧度记作1 ____
度
弧度
半径长
rad
2.弧度数:
提示:一定大小的圆心角α所对应的弧长与半径的比值是唯一确定的,与半径大小无关.
3.角度制与弧度制的换算:
4.角度制与弧度制的比较:
由于进位制不同,同一个角的弧度数与角度数一般是不同的.
[微思考] (1)半径不同的圆中,相同的圆心角所对的弧度数是否相同?
提示:相同.角的弧度数的大小与所在圆的半径的大小无关,只与圆心角的大小有关.
(2)2°与2弧度的角是否表示同一个角?
提示:不是同一个角.2°是角度制,2是弧度制,2 rad约为115°.
角度制 用度作为单位来度量角的单位制 单位“°”不能省略 角的正负与方向有关 六十进制
弧度制 用弧度作为单位来度量角的单位制 单位“rad”可以省略 角的正负与方向有关 十进制
5.一些特殊角与弧度数的对应关系:
0
2π
60°
180°
答案:C
知识点二 扇形的弧长和面积公式
(一)教材梳理填空
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则
(1)弧长公式:l= .
(2)扇形面积公式:S= = .
αR
(二)基本知能小试
1.判断正误:
(1)扇形的半径为1 cm,圆心角为30°,则扇形的弧长l=r|α|=1×30=30(cm). ( )
(2)若扇形的半径不变,圆心角扩大为原来的2倍,则扇形的弧长也扩大为原来的2倍. ( )
(3)若扇形的半径和弧长都变为原来的2倍,则扇形的面积变为原来的2倍.( )
答案:(1)× (2)√ (3)×
题型一 角度与弧度的换算
【学透用活】
角与实数的对应
(1)角的概念推广后,无论是用角度制还是用弧度制,都能在角的集合与实数集R之间建立一种一一对应的关系:即每一个角都有唯一的一个实数(如这个角的度数或弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(如弧度数或角度数等于这个实数的角)与它对应.
(2)由于弧度制的单位与实数单位一致,所以能给研究问题带来方便.
题型二 用弧度制表示角有关的角
【学透用活】
[典例2] 已知角α=2 005°.
(1)将α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出α是第几象限的角;
(2)在[-5π,0)内找出与α终边相同的角.
[方法技巧]
1.弧度制下与角α终边相同的角的表示
在弧度制下,与角α的终边相同的角可以表示为{β|β=2kπ+α,k∈Z},即与角α终边相同的角可以表示成α加上2π的整数倍.
2.根据已知图形写出区域角的集合的步骤
(1)仔细观察图形.
(2)写出区域边界作为终边时角的表示.
(3)用不等式表示区域范围内的角.
3.用弧度表示角的注意点
(1)注意角度与弧度不能混用.
(2)各终边相同的角需加2kπ,k∈Z.
(3)求两个角的集合的交集时,注意应用数轴直观确定,可对k进行适当的赋值.
2. 用弧度制表示终边在图中阴影区域内角的集合(包括边界),
并判断2 012°是不是这个集合的元素.
提示:应注意结果是圆心角的绝对值,具体应用时既要注意其大小,又要注意其正负.
(2)在使用弧度制下的弧长公式及面积公式时,若已知的角是以“度”为单位,需注意什么问题?
提示:若已知的角是以“度”为单位,则必须先把它化成弧度后再计算,否则结果易出错.
【学透用活】
[典例3] 已知扇形的周长为10 cm,面积为4 cm2,求扇形圆心角的弧度数.
[方法技巧]
1.弧度制下有关扇形弧长、面积问题的解题策略
涉及扇形的周长、弧长、圆心角、面积等的计算,关键是先分析题目已知哪些量求哪些量,然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解.
2 .扇形弧长、面积公式的变形运用
3 .谨记3个注意点
(1)在弧度制中的弧长公式及扇形面积公式中的圆心角可正可负.
(2)看清角的度量制,选用相应的公式.
(3)扇形的周长等于弧长加两个半径长.
【对点练清】
1.已知一扇形的圆心角是72°,半径为20,求扇形的面积.
2.已知扇形的周长为20 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
二、应用性——强调学以致用
2.某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇
环的周长为30米,其中大圆弧所在圆的半径为10米.设小
圆弧所在圆的半径为x米,圆心角为θ(弧度).
(1)求θ关于x的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.
[析题建模] (1)利用扇形的弧长公式,结合扇环面的周长,可求θ关于x的函数关系式.
(2)分别求出花坛的面积、装饰总费用,可求y关于x的函数关系式,然后换元,利用基本不等式求最大值.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
