5.1.1任意角 课件(共41张PPT)
文档属性
| 名称 | 5.1.1任意角 课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 907.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 16:59:45 | ||
图片预览










文档简介
(共41张PPT)
第五章 三角函数
5.1 任意角和弧度制
5.1.1 任意角
明确目标 发展素养
1.了解角的概念的推广过程,理解任意角的概念. 2.掌握终边相同角的含义及其表示. 3.掌握轴线角、象限角及区间角的表示方法. 1.通过终边相同角的计算,培养数学运算素养.
2.借助任意角的理解,培养数学抽象素养.
3.借助任意角的终边位置的确定,提升逻辑推理素养.
知识点一 任意角的概念
(一)教材梳理填空
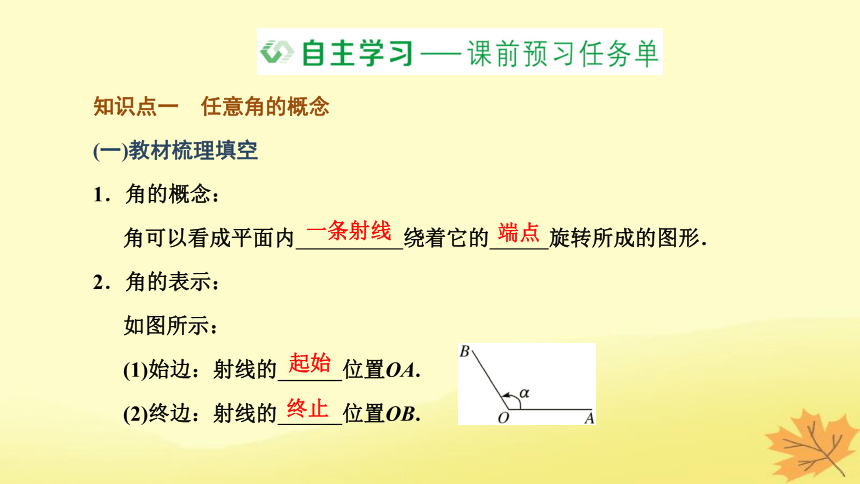
1.角的概念:
角可以看成平面内 绕着它的 旋转所成的图形.
2.角的表示:
如图所示:
(1)始边:射线的 位置OA.
(2)终边:射线的 位置OB.
一条射线
端点
起始
终止
(3)顶点:射线的端点O.
(4)记法:图中的角α可记为“角α”或“∠α”或“ ”.“角α”或“∠α”可简记为“α”.
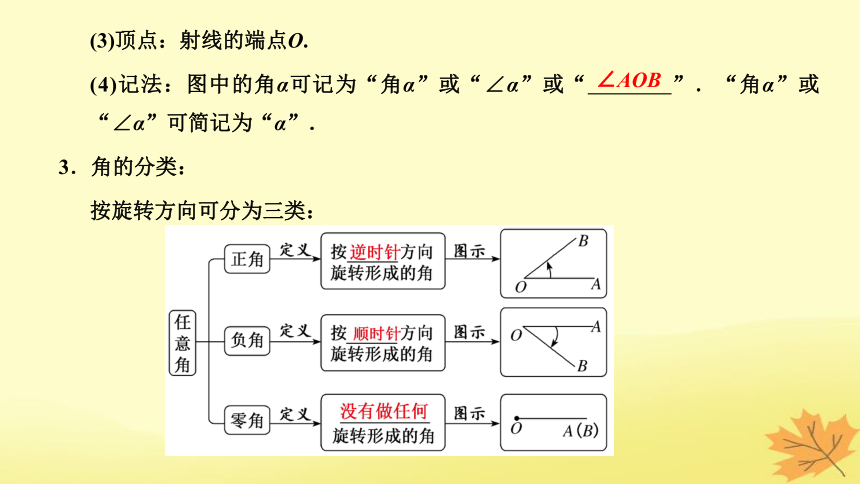
3.角的分类:
按旋转方向可分为三类:
∠AOB
4.角的加法与减法:
设α,β是任意两个角, 为角α的相反角.
(1)α+β:把角α的 旋转角β.
(2)α-β:α-β= .
-α
终边
α+(-β)
(二)基本知能小试
1.判断正误
(1)大于90°的角都是钝角. ( )
(2)零角的终边与始边重合. ( )
(3)一条射线绕端点旋转,旋转的圈数越多,则这个角越大. ( )
答案:(1)× (2)√ (3)×
2.将射线OM绕端点O按逆时针方向旋转120°所得的角为 ( )
A.120° B.-120°
C.240° D.-240°
答案:A
知识点二 象限角与终边相同的角
(一)教材梳理填空
1.象限角:
(1)象限角的概念:我们通常在直角坐标系内讨论角.为了方便,使角的顶点与 重合,角的始边与 重合,那么,角的终边在第几象限,就说这个角是 ___________ .
如果角的终边在 上,那么就认为这个角不属于任何一个象限.
坐标原点
x轴的非负半轴
第几象限角
坐标轴
(2)象限角的集合表示:
[微思考] “锐角”“第一象限角”“小于90°的角”三者有何不同?
提示:锐角是第一象限角,也是大于0°且小于90°的角;而第一象限角可以是锐角,也可以大于360°,还可能是负角;小于90°的角可以是锐角,也可以是零角或负角.
象限角 角的集合表示
第一象限角 _________________________________
第二象限角 {x|90°+k·360°<x<180°+k·360°,k∈Z}
第三象限角 {x|180°+k·360°<x<270°+k·360°,k∈Z}
第四象限角 __________________________________________
{x|k·360°<x<90°+k·360°,k∈Z}
{x|270°+k·360°<x<360°+k·360°,k∈Z}
2.终边相同的角:
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|_____________________},
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
β=α+k·360°,k∈Z
3.轴线角的集合:
角α终边的位置 角α的集合表示
在x轴的非负半轴上 {α|α=k·360°,k∈Z}
在x轴的非正半轴上 {α|α=k·360°+180°,k∈Z}
在y轴的非负半轴上 {α|α=k·360°+90°,k∈Z}
在y轴的非正半轴上 {α|α=k·360°+270°,k∈Z}
在x轴上 {α|α=k·180°,k∈Z}
在y轴上 {α|α=k·180°+90°,k∈Z}
在坐标轴上 {α|α=k·90°,k∈Z}
[微思考] 定义或求象限角、终边相同的角的前提条件是什么?
提示:定义或求象限角、终边相同的角时,必须注意前提条件:角的顶点与原点重合,始边与x轴的非负半轴重合.
(二)基本知能小试
1.判断正误
(1)第二象限角大于第一象限角. ( )
(2)第二象限角是钝角. ( )
(3)相等的角终边一定相同. ( )
(4)终边相同的角有无数个,它们相差360°的整数倍. ( )
答案:(1)× (2)× (3) √ (4)√
2.与45°角终边相同的角是 ( )
A.-45° B.225°
C.395° D.-315°
解析:因为45°=-315°+360°,所以与45°角终边相同的角是-315°.
答案:D
3.与610°角终边相同的角表示为(其中k∈Z) ( )
A.k·360°+230° B.k·360°+250°
C.k·360°+70° D.k·180°+270°
解析:∵610°=360°+250°,∴610°与250°角的终边相同,故选B.
答案:B
4.已知0°≤α<360°,且α与800°角终边相同,则α=________,它是第________象限角.
解析:因为800°=360°×2+80°,所以80°角与800°角的终边相同,且0°≤80°<360°,故α=80°,它是第一象限角.
答案:80° 一
题型一 任意角的概念及应用
【学透用活】
1.角的概念的推广
(1)角的概念是通过角的终边的运动来推广的,根据角的终边的旋转“方向”,得到正角、负角和零角.
(2)表示角时,应注意箭头的方向不可丢掉,箭头方向代表角的正负.
2.用旋转来描述角时需要注意的三个要素
(1)旋转中心:射线旋转时绕的端点.
(2)旋转方向:旋转变换的方向分为逆时针和顺时针两种,这是一对意义相反的量,根据以往的经验,我们可以把一对意义相反的量用正、负数来表示,那么许多问题就可以解决了.
(3)旋转量:当旋转超过一周时,旋转量即超过360°,角度的绝对值可大于360°.于是就会出现720°,-540°等角度.
[典例1] (1)(多选)下列说法正确的是 ( )
A.锐角都是第一象限角
B.第一象限角一定不是负角
C.小于180°的角是钝角、直角或锐角
D.在90°≤β<180°范围内的角β不一定是钝角
(2)已知角的顶点与坐标原点重合,始边与x轴的非负半轴重合,作出下列各角,并指出它们是第几象限角.
①420°;②855°;③-510°.
[解析] (1)锐角是大于0°且小于90°的角,终边落在第一象限,是第一象限角,所以A正确;-350°角是第一象限角,但它是负角,所以B错误;0°角是小于180°的角,但它既不是钝角,也不是直角或锐角,所以C错误;因为在90°≤β<180°范围内的角β包含90°角,所以不一定是钝角,所以D正确.
答案: (1) AD
(2)作出各角的终边,如图所示:
由图可知:①420°是第一象限角.②855°是第二象限角.
③-510°是第三象限角.
[方法技巧]
1.理解角的概念的关键与技巧
(1)关键:正确理解象限角与锐角、直角、钝角、平角、周角等概念.
(2)技巧:判断命题为真需要证明,而判断命题为假只要举出反例即可.
2.象限角的两种判定方法
(1)在坐标系中画出相应的角,观察终边的位置,确定象限.
(2)第一步,将α写成α=k·360°+β(k∈Z,0°≤β<360°)的形式;
第二步,判断β的终边所在的象限;
第三步,根据β的终边所在的象限,即可确定α的终边所在的象限.
[提醒] 理解任意角这一概念时,要注意“旋转方向”决定角的“正负”,“旋转幅度”决定角的“绝对值大小”.
【对点练清】
1.给出下列说法:
①终边在y轴非负半轴上的角是直角;
②始边相同而终边不同的角一定不相等;
③三角形的内角必是第一、二象限角;
④第四象限角一定是负角;
⑤{α|α=k·180°,k∈Z}={0°,180°,360°}.
其中正确说法的个数是 ( )
A.1 B.2 C.3 D.4
2.射线OA绕端点O顺时针旋转80°到OB位置,接着逆时针旋转250°到OC位置,然后再顺时针旋转270°到OD位置,则∠AOD=________.
解析:如图,∠AOD=∠AOB+∠BOC+∠COD
=(-80°)+250°+(-270°)
=-100°.
答案:-100°
题型二 终边相同的角的表示及应用
【学透用活】
对终边相同的角的说明
所有与角α终边相同的角,连同角α在内(而且只有这样的角),可以用式子α+k·360°,k∈Z表示.在运用时,需注意以下几点:
(1)k是整数,这个条件不能漏掉.
(2)α是任意角.
(3)k·360°与α之间用“+”号连接,如k·360°-30°应看成k·360°+(-30°)(k∈Z).
(4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数个,它们相差周角的整数倍.
[典例2] 在与10 030°角终边相同的角中,求满足下列条件的角:
(1)最大的负角;(2)-360°~720°范围内的角.
(2)由-360°≤10 030°+k·360°<720°,
得-10 390°≤k·360°<-9 310°.
又k∈Z,解得k=-28,-27,-26.
当k=-28时,β=10 030°-28×360°=-50°;
当k=-27时,β=10 030°-27×360°=310°;
当k=-26时,β=10 030°-26×360°=670°.
故所求的角β的值为-50°,310°,670°.
[方法技巧]
1.在某个范围内找与已知角终边相同的角的方法
求在某个范围内与已知角α终边相同的角时,首先将这样的角表示成k·360°+α(k∈Z)的形式,然后由k·360°+α(k∈Z)在限制范围内,建立不等式,通过求解不等式,确定k的值,求出满足条件的角.或者采用赋值法求解,看角是否在限制范围内,从而求出满足条件的角.
2.终边相同的角常用的三个结论
(1)终边相同的角之间相差360°的整数倍.
(2)终边在同一直线上的角之间相差180°的整数倍.
(3)终边在相互垂直的两直线上的角之间相差90°的整数倍.
【对点练清】
1.与-463°终边相同的角可以表示为 ( )
A.k·360°+463°(k∈Z) B.k·360°+103°(k∈Z)
C.k·360°+257°(k∈Z) D.k·360°-257°(k∈Z)
解析:因为-463°=257°-2×360°,所以与-463°终边相同的角可以表示为k·360°+257°(k∈Z).
答案:C
2.已知α=-1 910°.
(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,并指出它是第几象限的角;
(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.
题型三 区间角的表示
[探究发现]
(1)若射线OA的位置是k·360°+10°,k∈Z,射线OA绕点O逆时针旋转90°经过的区域为D,则终边落在区域D(包括边界)的角的集合应如何表示?
提示:终边落在区域D(包括边界)的角的集合可表示为{α|k·360°+10°≤α≤k·360°+100°,k∈Z}.
(2)若角α与β的终边关于x轴,y轴,原点,直线y=x对称,则角α与β分别具有怎样的关系?
提示:①关于x轴对称:若角α与β的终边关于x轴对称,则角α与β的关系是β=-α+k·360°,k∈Z.
②关于y轴对称:若角α与β的终边关于y轴对称,则角α与β的关系是β=180°-α+k·360°,k∈Z.
③关于原点对称:若角α与β的终边关于原点对称,则角α与β的关系是β=180°+α+k·360°,k∈Z.
④关于直线y=x对称:若角α与β的终边关于直线y=x对称,则角α与β的关系是β=-α+90°+k·360°,k∈Z.
【学透用活】
[典例3] 已知如图所示的图形.
(1)分别写出终边落在OA,OB位置上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.
[解] (1)终边落在OA位置上的角的集合为{α|α=90°+45°+k·360°,k∈Z}={α|α=135°+k·360°,k∈Z};
终边落在OB位置上的角的集合为{α|α=-30°+k·360°,k∈Z}.
(2)由题干图可知,阴影部分(包括边界)的角的集合是由所有在-30°~135°范围内的与之终边相同的角组成的集合,故该区域可表示为{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}.
[方法技巧]
1.象限角的判定方法
(1)根据图象判定.利用图象实际操作时,依据是终边相同的角的思想,因为在0°~360°范围内的角与直角坐标系中的射线可建立一一对应的关系.
(2)将角转化到在0°~360°范围内.在直角坐标系内,在0°~360°范围内没有两个角终边是相同的.
2.表示区间角的三个步骤
(1)先按逆时针的方向找到区域的起始和终止边界.
(2)按由小到大分别标出起始和终止边界对应的在-360°~360°范围内的角α和β,写出最简区间{x|α(3)起始、终止边界对应角α,β再加上360°的整数倍,即得区间角集合.
【对点练清】
1.[变条件]若将本例改为如图所示的图形,那么阴影部分(包括边界)
表示的终边相同的角的集合如何表示?
解:在0°~360°范围内,阴影部分(包括边界)表示的范围可
表示为150°≤β ≤225°,则所有满足条件的角β为
{β|k·360°+150°≤β≤k·360°+225°,k∈Z}.
2.[变条件]若将本例改为如图所示的图形,那么终边落在阴影部分
(实线包括边界)的角的集合如何表示?
解:在0°~360°范围内,终边落在阴影部分的角为60°≤β<105°与240°≤β <285°,所以所有满足题意的角β为{β|k·360°+60°≤β<
k·360°+105°,k∈Z}∪{β|k·360°+240°≤β <k·360°+285°,k∈Z}={β|2k·180°+60°≤β <2k·180°+105°,k∈Z}∪{β|(2k+1)·180°+60°≤β <(2k+1)·180°+105°,k∈Z}={β|n·180°+60°≤β <n·180°+105°,n∈Z}.故角β的取值集合为{β|n·180°+60°≤β<n·180°+105°,n∈Z}.
问题1:你能用另一种方法验证上述解法的正确性吗?
问题4:通过以上问题的求解方法,你能得出什么结论?
二、应用性——强调学以致用
一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,
若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,红蚂蚁每秒爬
过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两
只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β
的值.
[析题建模]
第五章 三角函数
5.1 任意角和弧度制
5.1.1 任意角
明确目标 发展素养
1.了解角的概念的推广过程,理解任意角的概念. 2.掌握终边相同角的含义及其表示. 3.掌握轴线角、象限角及区间角的表示方法. 1.通过终边相同角的计算,培养数学运算素养.
2.借助任意角的理解,培养数学抽象素养.
3.借助任意角的终边位置的确定,提升逻辑推理素养.
知识点一 任意角的概念
(一)教材梳理填空
1.角的概念:
角可以看成平面内 绕着它的 旋转所成的图形.
2.角的表示:
如图所示:
(1)始边:射线的 位置OA.
(2)终边:射线的 位置OB.
一条射线
端点
起始
终止
(3)顶点:射线的端点O.
(4)记法:图中的角α可记为“角α”或“∠α”或“ ”.“角α”或“∠α”可简记为“α”.
3.角的分类:
按旋转方向可分为三类:
∠AOB
4.角的加法与减法:
设α,β是任意两个角, 为角α的相反角.
(1)α+β:把角α的 旋转角β.
(2)α-β:α-β= .
-α
终边
α+(-β)
(二)基本知能小试
1.判断正误
(1)大于90°的角都是钝角. ( )
(2)零角的终边与始边重合. ( )
(3)一条射线绕端点旋转,旋转的圈数越多,则这个角越大. ( )
答案:(1)× (2)√ (3)×
2.将射线OM绕端点O按逆时针方向旋转120°所得的角为 ( )
A.120° B.-120°
C.240° D.-240°
答案:A
知识点二 象限角与终边相同的角
(一)教材梳理填空
1.象限角:
(1)象限角的概念:我们通常在直角坐标系内讨论角.为了方便,使角的顶点与 重合,角的始边与 重合,那么,角的终边在第几象限,就说这个角是 ___________ .
如果角的终边在 上,那么就认为这个角不属于任何一个象限.
坐标原点
x轴的非负半轴
第几象限角
坐标轴
(2)象限角的集合表示:
[微思考] “锐角”“第一象限角”“小于90°的角”三者有何不同?
提示:锐角是第一象限角,也是大于0°且小于90°的角;而第一象限角可以是锐角,也可以大于360°,还可能是负角;小于90°的角可以是锐角,也可以是零角或负角.
象限角 角的集合表示
第一象限角 _________________________________
第二象限角 {x|90°+k·360°<x<180°+k·360°,k∈Z}
第三象限角 {x|180°+k·360°<x<270°+k·360°,k∈Z}
第四象限角 __________________________________________
{x|k·360°<x<90°+k·360°,k∈Z}
{x|270°+k·360°<x<360°+k·360°,k∈Z}
2.终边相同的角:
所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|_____________________},
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
β=α+k·360°,k∈Z
3.轴线角的集合:
角α终边的位置 角α的集合表示
在x轴的非负半轴上 {α|α=k·360°,k∈Z}
在x轴的非正半轴上 {α|α=k·360°+180°,k∈Z}
在y轴的非负半轴上 {α|α=k·360°+90°,k∈Z}
在y轴的非正半轴上 {α|α=k·360°+270°,k∈Z}
在x轴上 {α|α=k·180°,k∈Z}
在y轴上 {α|α=k·180°+90°,k∈Z}
在坐标轴上 {α|α=k·90°,k∈Z}
[微思考] 定义或求象限角、终边相同的角的前提条件是什么?
提示:定义或求象限角、终边相同的角时,必须注意前提条件:角的顶点与原点重合,始边与x轴的非负半轴重合.
(二)基本知能小试
1.判断正误
(1)第二象限角大于第一象限角. ( )
(2)第二象限角是钝角. ( )
(3)相等的角终边一定相同. ( )
(4)终边相同的角有无数个,它们相差360°的整数倍. ( )
答案:(1)× (2)× (3) √ (4)√
2.与45°角终边相同的角是 ( )
A.-45° B.225°
C.395° D.-315°
解析:因为45°=-315°+360°,所以与45°角终边相同的角是-315°.
答案:D
3.与610°角终边相同的角表示为(其中k∈Z) ( )
A.k·360°+230° B.k·360°+250°
C.k·360°+70° D.k·180°+270°
解析:∵610°=360°+250°,∴610°与250°角的终边相同,故选B.
答案:B
4.已知0°≤α<360°,且α与800°角终边相同,则α=________,它是第________象限角.
解析:因为800°=360°×2+80°,所以80°角与800°角的终边相同,且0°≤80°<360°,故α=80°,它是第一象限角.
答案:80° 一
题型一 任意角的概念及应用
【学透用活】
1.角的概念的推广
(1)角的概念是通过角的终边的运动来推广的,根据角的终边的旋转“方向”,得到正角、负角和零角.
(2)表示角时,应注意箭头的方向不可丢掉,箭头方向代表角的正负.
2.用旋转来描述角时需要注意的三个要素
(1)旋转中心:射线旋转时绕的端点.
(2)旋转方向:旋转变换的方向分为逆时针和顺时针两种,这是一对意义相反的量,根据以往的经验,我们可以把一对意义相反的量用正、负数来表示,那么许多问题就可以解决了.
(3)旋转量:当旋转超过一周时,旋转量即超过360°,角度的绝对值可大于360°.于是就会出现720°,-540°等角度.
[典例1] (1)(多选)下列说法正确的是 ( )
A.锐角都是第一象限角
B.第一象限角一定不是负角
C.小于180°的角是钝角、直角或锐角
D.在90°≤β<180°范围内的角β不一定是钝角
(2)已知角的顶点与坐标原点重合,始边与x轴的非负半轴重合,作出下列各角,并指出它们是第几象限角.
①420°;②855°;③-510°.
[解析] (1)锐角是大于0°且小于90°的角,终边落在第一象限,是第一象限角,所以A正确;-350°角是第一象限角,但它是负角,所以B错误;0°角是小于180°的角,但它既不是钝角,也不是直角或锐角,所以C错误;因为在90°≤β<180°范围内的角β包含90°角,所以不一定是钝角,所以D正确.
答案: (1) AD
(2)作出各角的终边,如图所示:
由图可知:①420°是第一象限角.②855°是第二象限角.
③-510°是第三象限角.
[方法技巧]
1.理解角的概念的关键与技巧
(1)关键:正确理解象限角与锐角、直角、钝角、平角、周角等概念.
(2)技巧:判断命题为真需要证明,而判断命题为假只要举出反例即可.
2.象限角的两种判定方法
(1)在坐标系中画出相应的角,观察终边的位置,确定象限.
(2)第一步,将α写成α=k·360°+β(k∈Z,0°≤β<360°)的形式;
第二步,判断β的终边所在的象限;
第三步,根据β的终边所在的象限,即可确定α的终边所在的象限.
[提醒] 理解任意角这一概念时,要注意“旋转方向”决定角的“正负”,“旋转幅度”决定角的“绝对值大小”.
【对点练清】
1.给出下列说法:
①终边在y轴非负半轴上的角是直角;
②始边相同而终边不同的角一定不相等;
③三角形的内角必是第一、二象限角;
④第四象限角一定是负角;
⑤{α|α=k·180°,k∈Z}={0°,180°,360°}.
其中正确说法的个数是 ( )
A.1 B.2 C.3 D.4
2.射线OA绕端点O顺时针旋转80°到OB位置,接着逆时针旋转250°到OC位置,然后再顺时针旋转270°到OD位置,则∠AOD=________.
解析:如图,∠AOD=∠AOB+∠BOC+∠COD
=(-80°)+250°+(-270°)
=-100°.
答案:-100°
题型二 终边相同的角的表示及应用
【学透用活】
对终边相同的角的说明
所有与角α终边相同的角,连同角α在内(而且只有这样的角),可以用式子α+k·360°,k∈Z表示.在运用时,需注意以下几点:
(1)k是整数,这个条件不能漏掉.
(2)α是任意角.
(3)k·360°与α之间用“+”号连接,如k·360°-30°应看成k·360°+(-30°)(k∈Z).
(4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数个,它们相差周角的整数倍.
[典例2] 在与10 030°角终边相同的角中,求满足下列条件的角:
(1)最大的负角;(2)-360°~720°范围内的角.
(2)由-360°≤10 030°+k·360°<720°,
得-10 390°≤k·360°<-9 310°.
又k∈Z,解得k=-28,-27,-26.
当k=-28时,β=10 030°-28×360°=-50°;
当k=-27时,β=10 030°-27×360°=310°;
当k=-26时,β=10 030°-26×360°=670°.
故所求的角β的值为-50°,310°,670°.
[方法技巧]
1.在某个范围内找与已知角终边相同的角的方法
求在某个范围内与已知角α终边相同的角时,首先将这样的角表示成k·360°+α(k∈Z)的形式,然后由k·360°+α(k∈Z)在限制范围内,建立不等式,通过求解不等式,确定k的值,求出满足条件的角.或者采用赋值法求解,看角是否在限制范围内,从而求出满足条件的角.
2.终边相同的角常用的三个结论
(1)终边相同的角之间相差360°的整数倍.
(2)终边在同一直线上的角之间相差180°的整数倍.
(3)终边在相互垂直的两直线上的角之间相差90°的整数倍.
【对点练清】
1.与-463°终边相同的角可以表示为 ( )
A.k·360°+463°(k∈Z) B.k·360°+103°(k∈Z)
C.k·360°+257°(k∈Z) D.k·360°-257°(k∈Z)
解析:因为-463°=257°-2×360°,所以与-463°终边相同的角可以表示为k·360°+257°(k∈Z).
答案:C
2.已知α=-1 910°.
(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,并指出它是第几象限的角;
(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.
题型三 区间角的表示
[探究发现]
(1)若射线OA的位置是k·360°+10°,k∈Z,射线OA绕点O逆时针旋转90°经过的区域为D,则终边落在区域D(包括边界)的角的集合应如何表示?
提示:终边落在区域D(包括边界)的角的集合可表示为{α|k·360°+10°≤α≤k·360°+100°,k∈Z}.
(2)若角α与β的终边关于x轴,y轴,原点,直线y=x对称,则角α与β分别具有怎样的关系?
提示:①关于x轴对称:若角α与β的终边关于x轴对称,则角α与β的关系是β=-α+k·360°,k∈Z.
②关于y轴对称:若角α与β的终边关于y轴对称,则角α与β的关系是β=180°-α+k·360°,k∈Z.
③关于原点对称:若角α与β的终边关于原点对称,则角α与β的关系是β=180°+α+k·360°,k∈Z.
④关于直线y=x对称:若角α与β的终边关于直线y=x对称,则角α与β的关系是β=-α+90°+k·360°,k∈Z.
【学透用活】
[典例3] 已知如图所示的图形.
(1)分别写出终边落在OA,OB位置上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.
[解] (1)终边落在OA位置上的角的集合为{α|α=90°+45°+k·360°,k∈Z}={α|α=135°+k·360°,k∈Z};
终边落在OB位置上的角的集合为{α|α=-30°+k·360°,k∈Z}.
(2)由题干图可知,阴影部分(包括边界)的角的集合是由所有在-30°~135°范围内的与之终边相同的角组成的集合,故该区域可表示为{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}.
[方法技巧]
1.象限角的判定方法
(1)根据图象判定.利用图象实际操作时,依据是终边相同的角的思想,因为在0°~360°范围内的角与直角坐标系中的射线可建立一一对应的关系.
(2)将角转化到在0°~360°范围内.在直角坐标系内,在0°~360°范围内没有两个角终边是相同的.
2.表示区间角的三个步骤
(1)先按逆时针的方向找到区域的起始和终止边界.
(2)按由小到大分别标出起始和终止边界对应的在-360°~360°范围内的角α和β,写出最简区间{x|α
【对点练清】
1.[变条件]若将本例改为如图所示的图形,那么阴影部分(包括边界)
表示的终边相同的角的集合如何表示?
解:在0°~360°范围内,阴影部分(包括边界)表示的范围可
表示为150°≤β ≤225°,则所有满足条件的角β为
{β|k·360°+150°≤β≤k·360°+225°,k∈Z}.
2.[变条件]若将本例改为如图所示的图形,那么终边落在阴影部分
(实线包括边界)的角的集合如何表示?
解:在0°~360°范围内,终边落在阴影部分的角为60°≤β<105°与240°≤β <285°,所以所有满足题意的角β为{β|k·360°+60°≤β<
k·360°+105°,k∈Z}∪{β|k·360°+240°≤β <k·360°+285°,k∈Z}={β|2k·180°+60°≤β <2k·180°+105°,k∈Z}∪{β|(2k+1)·180°+60°≤β <(2k+1)·180°+105°,k∈Z}={β|n·180°+60°≤β <n·180°+105°,n∈Z}.故角β的取值集合为{β|n·180°+60°≤β<n·180°+105°,n∈Z}.
问题1:你能用另一种方法验证上述解法的正确性吗?
问题4:通过以上问题的求解方法,你能得出什么结论?
二、应用性——强调学以致用
一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,
若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,红蚂蚁每秒爬
过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两
只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β
的值.
[析题建模]
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
