第24章 圆(培优篇)-2022-2023学年九年级数学上册单元复习效果通关检测(人教版)
文档属性
| 名称 | 第24章 圆(培优篇)-2022-2023学年九年级数学上册单元复习效果通关检测(人教版) |  | |
| 格式 | doc | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-24 10:01:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第24章 圆(培优篇)
一、单选题(本大题共10小题,每小题3分,共30分)
1.如图,PQ是半⊙O的直径,两 ( http: / / www.21cnjy.com )正方形彼此相邻且内接于半圆,E是CD中点,若小正方形的边长为4cm,则该半圆的直径PQ的长为( )
( http: / / www.21cnjy.com / )
A.cm B.cm C.cm D.cm
2.已知⊙O的直径CD=100cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=96cm,则AC的长为( )21cnjy.com
A.36cm或64cm B.60cm或80cm C.80cm D.60cm
3.如图,在半圆中,直径,是半圆上一点,将弧沿弦折叠交于,点是弧的中点.连接,则的最小值为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
4.在平面直角坐标系中,已知点A(0,1),B(0,﹣5),若在x轴正半轴上有一点C,使∠ACB=30°,则点C的横坐标是( )21教育网
A.34 B.12 C.6+3 D.6
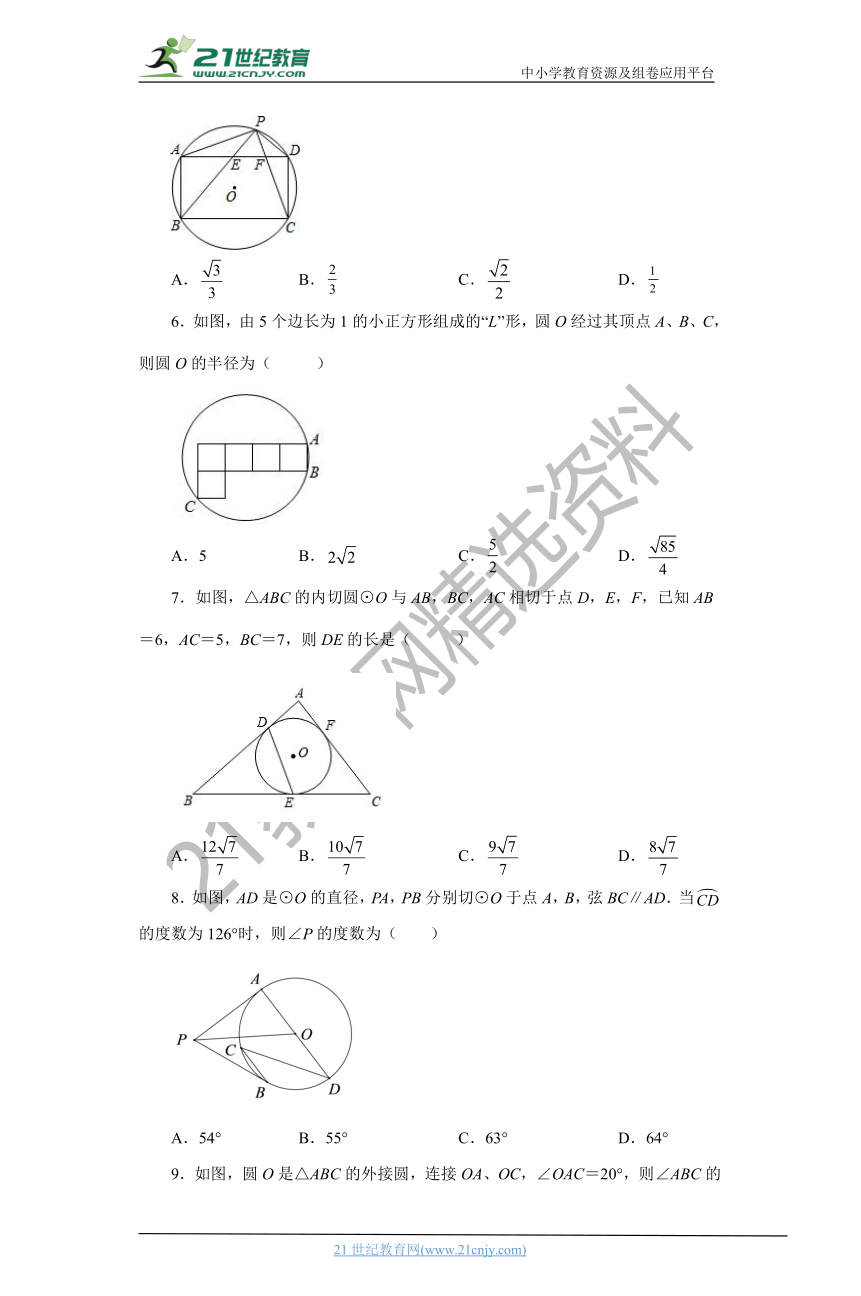
5.如图,⊙O的半径为1,点A、B、C、D ( http: / / www.21cnjy.com )在⊙O上,且四边形ABCD是矩形,点P是劣弧AD上一动点,PB、PC分别与AD相交于点E、点F.当PA=AB且AE=EF=FD时,AE的长度为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A. B. C. D.
6.如图,由5个边长为1的小正方形组成的“L”形,圆O经过其顶点A、B、C,则圆O的半径为( )
( http: / / www.21cnjy.com / )
A.5 B. C. D.
7.如图,△ABC的内切圆⊙O与AB,BC,AC相切于点D,E,F,已知AB=6,AC=5,BC=7,则DE的长是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图,AD是⊙O的直径,PA,PB分别切⊙O于点A,B,弦BC∥AD.当的度数为126°时,则∠P的度数为( )
( http: / / www.21cnjy.com / )
A.54° B.55° C.63° D.64°
9.如图,圆O是△ABC的外接圆,连接OA、OC,∠OAC=20°,则∠ABC的度数为( )
( http: / / www.21cnjy.com / )
A.140° B.110° C.70° D.40°
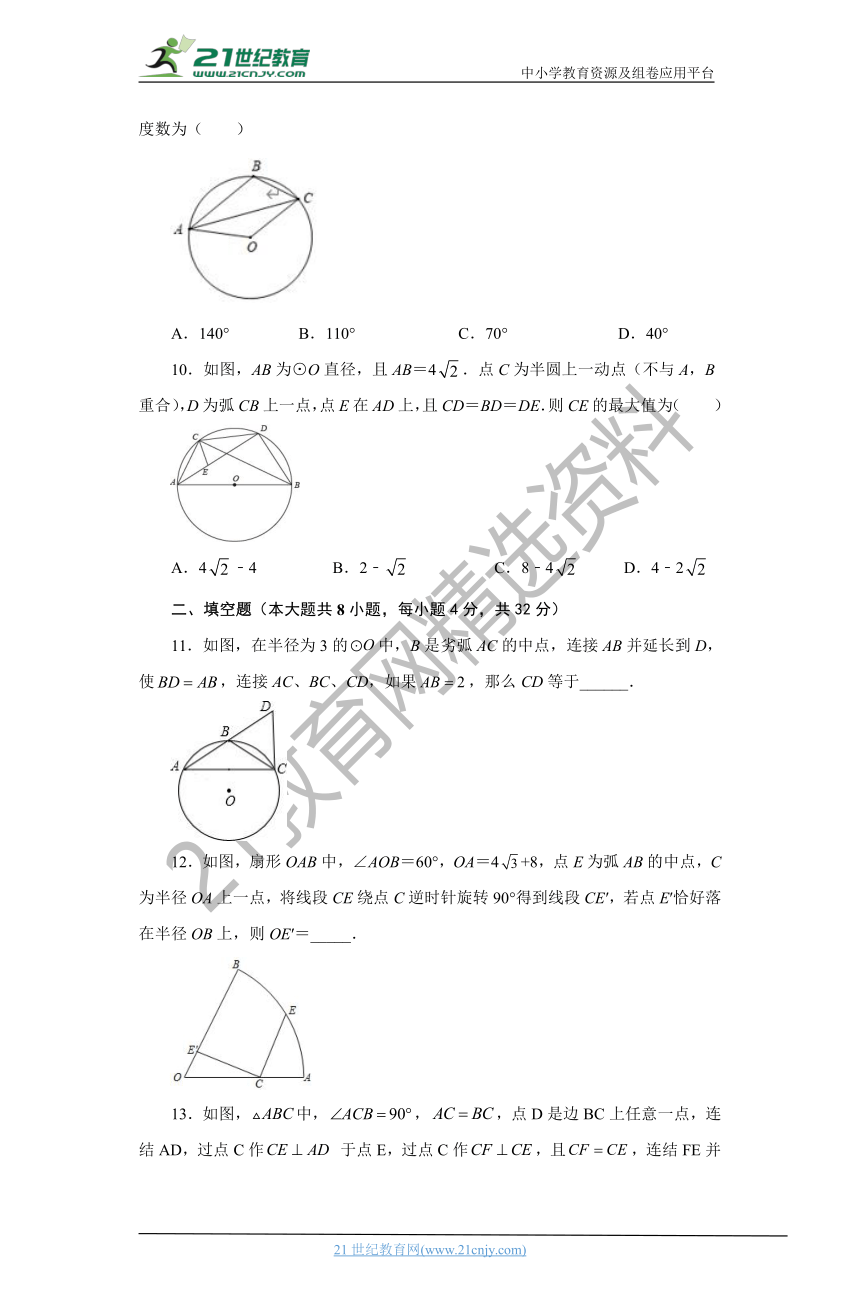
10.如图,AB为⊙O直径,且AB=4.点C为半圆上一动点(不与A,B重合),D为弧CB上一点,点E在AD上,且CD=BD=DE.则CE的最大值为( )
( http: / / www.21cnjy.com / )
A.4﹣4 B.2﹣ C.8﹣4 D.4﹣2
2、填空题(本大题共8小题,每小题4分,共32分)
11.如图,在半径为3的中,B是劣弧AC的中点,连接AB并延长到D,使,连接AC、BC、CD,如果,那么CD等于______.
( http: / / www.21cnjy.com / )
12.如图,扇形OAB中,∠AOB=60°,OA=4+8,点E为弧AB的中点,C为半径OA上一点,将线段CE绕点C逆时针旋转90°得到线段CE′,若点E′恰好落在半径OB上,则OE′=_____.21·cn·jy·com
( http: / / www.21cnjy.com / )
13.如图,中,,,点D是边BC上任意一点,连结AD,过点C作 于点E,过点C作,且,连结FE并延长交AB于点M,连结BF.若四边形AMEC的面积是8,,则四边形ABFC的面积是________.
( http: / / www.21cnjy.com / )
14.如图,在五边形AECDE中 ( http: / / www.21cnjy.com ),∠A=∠B=∠C=90°,AE=2,CD=1,以DE为直径的半圆分别与AB、BC相切于点F、G,则DE的长为______.
( http: / / www.21cnjy.com / )
15.如图,是的弦,,点P是优弧上的动点,,连接、,是的中线,(1)若,则____________;(2)的最大值=______________.
( http: / / www.21cnjy.com / )
16.如图所示,直线与x轴、y轴分别交于点M,N,的半径为1,将以每秒1个单位的速度向右作平移运动,当移动_________秒时,直线恰好与相切.
( http: / / www.21cnjy.com / )
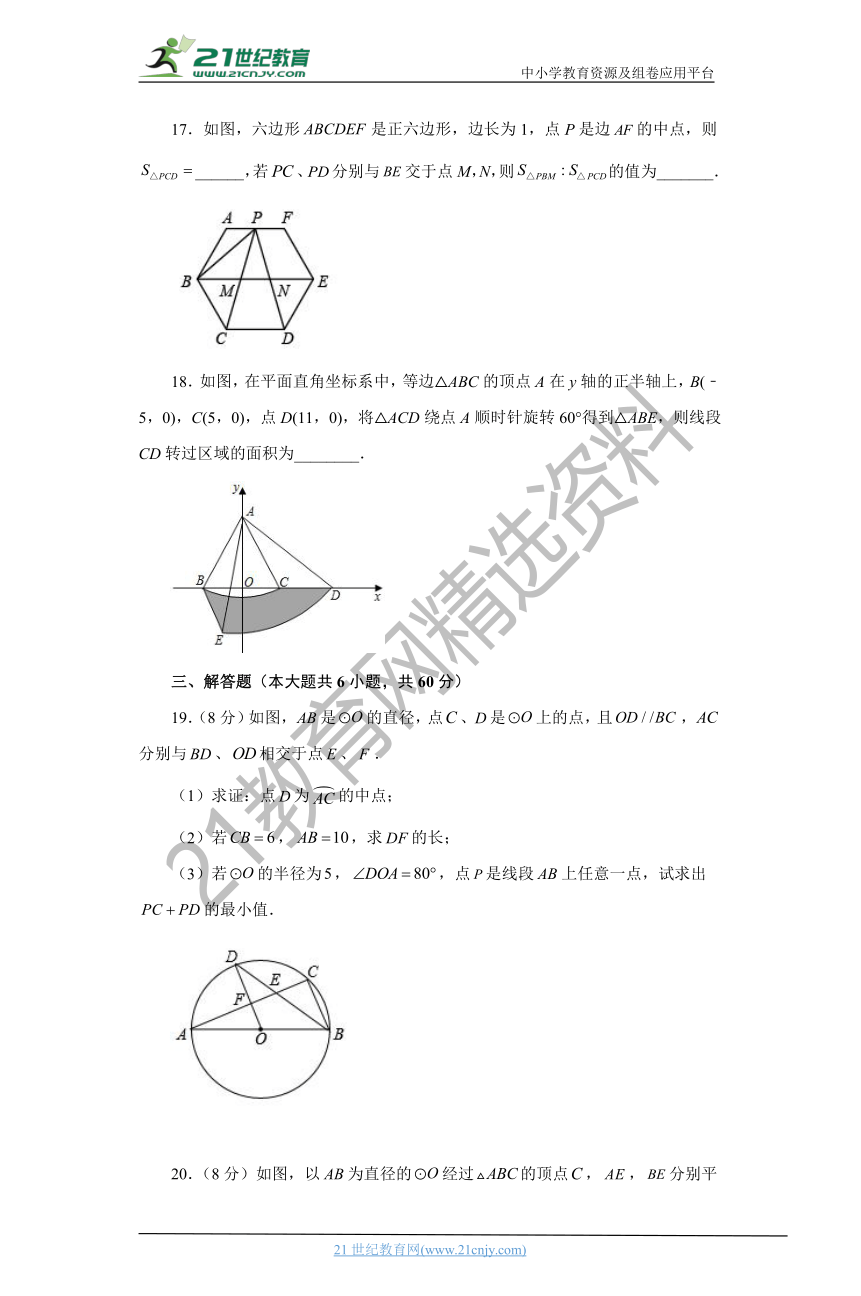
17.如图,六边形是正六边形,边长为1,点P是边的中点,则______,若、分别与交于点M,N,则的值为_______.
( http: / / www.21cnjy.com / )
18.如图,在平面直角坐标系 ( http: / / www.21cnjy.com )中,等边△ABC的顶点A在y轴的正半轴上,B(﹣5,0),C(5,0),点D(11,0),将△ACD绕点A顺时针旋转60°得到△ABE,则线段CD转过区域的面积为________.
( http: / / www.21cnjy.com / )
三、解答题(本大题共6小题,共60分)
19.(8分)如图,是的直径,点、是上的点,且,分别与、相交于点、.
(1)求证:点为的中点;
(2)若,,求的长;
(3)若的半径为,,点是线段上任意一点,试求出的最小值.
( http: / / www.21cnjy.com / )
20.(8分)如图,以为直径的经过的顶点,,分别平分和,的延长线交于点,连接.
(1) 判断的形状,并证明你的结论;
(2) 若,,求的长.
( http: / / www.21cnjy.com / )
21.(10分)如图,AB是⊙O的直径,,连接DE、DB,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)求证:DE=DM;
(2)若OA=CD=2,求阴影部分的面积.
( http: / / www.21cnjy.com / )
22.(10分)如图,的内接四边形ABCD两组对边的延长线分别交于点M,N.
(1)当∠M=∠N=42°时,求∠A的度数;
(2)若,且,请你用含有、的代数式表示∠A的度数.
( http: / / www.21cnjy.com / )
23.(10分)如图,以AB为直径的上有一动点C,的切线CD交AB的延长线于点D,过点B作交于点M,连接AM,OM,BC.
(1) 求证:
(2) 若,填空:
① 当AM= 时,四边形OCBM为菱形;
② 连接MD,过点O作于点N,若 ,则ON= .
( http: / / www.21cnjy.com / )
24.(12分)已知为的外接圆,,点是劣弧上一点(不与点,重合),连接,,.
(1)如图1,若是直径,将绕点逆时针旋转得到.若,求四边形的面积;
(2)如图2,若,半径为2,设线段的长为.四边形的面积为.
①求与的函数关系式;
②若点,分别在线段,上运动(不含端点),经过探究发现,点运动到每一个确定的位置.的周长有最小值,随着点的运动,的值会发生变化.求所有值中的最大值,并求此时四边形的面积.
( http: / / www.21cnjy.com / )
参考答案
1.D
【分析】
连接半径OB、OC、OF,可通过HL证明,得到OD=,最后运用勾股定理求解即可.
( http: / / www.21cnjy.com / )
解:如图,连接半径OB、OC、OF,则OB=OC=OF,
在正方形ABCD中,AB=CD,
(HL),
∴OA=OD,OD=,
E是CD中点,小正方形的边长为4cm,
∴DE=4cm,CD=8cm,OD=4cm,
,
∴该半圆的直径为2OC=cm.
故选:D.
【点拨】本题考查了全等三角形、勾股定理,属于综合题,能够熟练掌握各个知识点,并运用数形结合的思想是解题的关键.21·世纪*教育网
2.B
【分析】
分两种情况讨论,根据题意画出图形,根据垂径定理求出AM的长,连接OA,由勾股定理求出OM的长,进而可得出结论.【来源:21cnj*y.co*m】
解:连接AC,AO,
∵⊙O的直径CD=100cm,AB⊥CD,AB=96cm,
∴AM=AB=×96=48(cm),OD=OC=50(cm),
如图1,∵OA=50cm,AM=48cm,CD⊥AB,
∴OM===14(cm),
∴CM=OC+OM=50+14=64(cm),
∴AC===80(cm);
如图2,同理可得,OM=14cm,
∵OC=50cm,
∴MC==36(cm),
在Rt△AMC中,AC==60(cm);
综上所述,AC的长为80cm或60cm,
故选:B.
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
【点拨】本题考查的是垂径定理、勾股定理的应用,根据题意画出图形、利用垂径定理和勾股定理求解是解答此题的关键.21教育名师原创作品
3.D
【分析】
把弧AEC的圆补全为⊙F,可知点F与点O关于AC对称,求出∠F=90°,CE长,OE的最小值为EC-OC.
解:把弧AEC的圆补全为⊙F,可知点F与点O关于AC对称,半径为2,
∴∠FCA=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠FCA=∠CAO,
∴CF∥AB,
∵是弧的中点,
∴FE⊥AB,
∴∠F=∠BGE=90°,
∵FC=FE=2,
∴EC=,
∵OE≥EC-OC
即OE≥-2,
的最小值为,
故选:D.
( http: / / www.21cnjy.com / )
【点拨】本题考查了轴对称、垂径定理、勾股定理和圆的有关知识,解题关键是通过作辅助线,根据三角形三边关系确定OE的取值范围.
4.A
【分析】
如图,作的外接圆 连接 过作轴于 作轴于 则四边形是矩形,再证明是等边三角形,再分别求解即可得到答案.
解:如图,作的外接圆 连接 过作轴于 作轴于 则四边形是矩形,
( http: / / www.21cnjy.com / )
是等边三角形,
故选:
【点拨】本题考查的是坐标与图形, ( http: / / www.21cnjy.com )三角形的外接圆的性质,圆周角定理,等边三角形的判定与性质,矩形的判定与性质,勾股定理分应用,灵活应用以上知识解题是解题的关键.
5.A
【分析】
作辅助线,构建矩形的对角线,根据等边对 ( http: / / www.21cnjy.com )等角得∠ABP=∠APB,由同弧所对的圆周角相等可得∠ACB=∠ACP,根据矩形的四个角都是直角得∠ABC=90°,AE=EF=FD得FC=2FD,∠DCF=30°,得出∠ACB=30°,求出BC的长,则可得AD的长,再三等分即可.21*cnjy*com
解:连接AC、BD,
( http: / / www.21cnjy.com / )
∵PA=AB,
∴∠ABP=∠APB,
∵∠ABP=∠ACP,∠APB=∠ACB,
∴∠ACB=∠ACP,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠ACP=∠DAC,
∴AF=CF,
∵AE=EF=FD,
∴AF=DE=CF,则FC=2FD,
设FD=x,则FC=AF=2x,
∵四边形ABCD为矩形,
∴AD=BC,∠ABC=∠ADC=∠BCD=90°,
∴AC为⊙O的直径,
在Rt△DFC中,FC=2FD,
∴∠DCF=30°,
∴∠ACB=∠ACP=30°,
∵⊙O的半径为1,
∴AC=2,
∴AB=1,BC,
∴AD=BC,
∵AE=EF=FD,
∴AE.
故选:A.
【点拨】本题是有关圆的计算题,考查了矩形 ( http: / / www.21cnjy.com ),含30°的直角三角形的性质、等腰三角形的性质及圆周角、圆心角、弦、弧之间的关系,熟练掌握矩形的四个角都是直角,对角线相等且平分;在同圆或等圆中,同弧或等弧所对的圆周角相等.
6.D
【分析】
取AB的中点E,作,取圆心O,连接OB、OC,根据圆的性质,再结合勾股定理即可求解;
解:取AB的中点E,作,取圆心O,连接OB、OC,
( http: / / www.21cnjy.com / )
则
∵
设
解得:
∴
故选:D
【点拨】本题主要考查圆的性质、勾股定理,掌握相关知识并正确作出辅助线是解题的关键.
7.D
【分析】
连接、、,交于,作交BC于点G,利用 ,求出,进一步可得,求出,设⊙的半径为,利用,求出,求出,进一求出,再证明OB垂直平分,利用面积法可得,求得HE长即可求得答案.【来源:21·世纪·教育·网】
解:连接、、,交于,作交BC于点G,如图,
( http: / / www.21cnjy.com / )
∵AB=6,AC=5,BC=7,
∴,即,解得:,
∴,
∴,
设内切圆的半径为r,
则,解得:,
的内切圆⊙与,,分别相切于点,,,
∴∠ODB=∠OEB=90°,
又∵OD=OE, OB=OB,
∴,
∴BD=BE,
同理, CE=CF,AD=AF,
∵BE+CE=BC=7,
∴BD+BE+CE+CF=14,
∴2AD=(6+5+7)-14=4,即AD=2,
∴,
∴,
,,
垂直平分,
,,
,
,
,
故选:D.
【点拨】本题考查了三角形的内切圆性质,全等三角形的性质与判定,勾股定理,面积法等,正确添加辅助线,灵活运用相关知识是解题的关键.
8.A
【分析】
根据弧与圆心角的关系,可得,继而可得,根据平行线的性质以及同弧所对的圆周角相等,圆周角定理可得,根据领补角相等可得,根据切线长的性质以及切线的性质求得,进而求得,即可求得.【版权所有:21教育】
解:如图,连接,,,
( http: / / www.21cnjy.com / )
的度数为126°,
.
,
.
,
.
,
,,
.
,是⊙的切线,
,,,
.
故选A.
【点拨】本题考查了弧与圆心角的关系,平行线的性质,圆周角定理,同弧所对的圆周角相等,切线的性质,切线长定理,综合运用以上知识是解题的关键.
9.B
【分析】
根据OA=OC得到∠OAC=∠ ( http: / / www.21cnjy.com )OCA=20°,进而得到∠AOC=140°,在优弧AC上任取一点D,得到∠ADC=70°,然后根据内接四边形的性质即可求解.
解:∵OA=OC,∠OAC=20°
∴∠OAC=∠OCA=20°,
∴∠AOC=180°﹣20°×2=140°,
在优弧AC上任取一点D,连接AD、CD,如下图所示,
( http: / / www.21cnjy.com / )
∴∠ADC=70°
∴根据内接四边形的性质∠ABC=180°-70°=110°
故选:B.
【点拨】本题主要考查了等腰三角形的性质,圆周角定理,内接四边形的性质,作出辅助线是本题的关键.
10.A
【分析】
设,利用等弦对等弧,等弧所对的圆周角相等,等边对等角,三角形的外角的性质,通过角度的变换求得,确定的位置,进而证明,得到的运动轨迹是以点为圆心,4为半径的圆弧,进而根据直径是最长的弦求解即可.【出处:21教育名师】
解:延长,交于点,连接,OF
( http: / / www.21cnjy.com / )
设
CD=BD
为直径
在以点为圆心,4为半径的圆弧上运动,
,当为的直径时,取得最大值,最大值为
故选A
【点拨】本题考查了等弧所对的圆周角相等,弦与弧之间关系,找到点的运动轨迹,理解直径是最长的弦是解题的关键.
11.
【分析】
如图,连OA,OB.利用垂径定理和勾股定理求BE,利用中位线定理求CD.
解:如图,连OA,OB,
( http: / / www.21cnjy.com / )
∵B是弧AC的中点,AB=BC=BD,
∴△ACD是直角三角形,∠ACD=90°,
由垂径定理知,OB⊥AC,点E是AC的中点,
设,则,
由勾股定理知,, ,
∴,
∵AB=2,AO=BO=3,
∴,
解得, ,
即
∵∠AEB=∠ACD=90°,
∴BE∥CD,
∵点B是AD的中点,所以BE是△ACD的中位线,所以CD=2BE= .
故答案为:
【点拨】本题利用了垂径定理,勾股定理求解
12.
【分析】
过点作于,过点作于,连接,如图,设,利用得到,,再利用点为弧的中点得到,所以,,接着证明△,则,,则可列方程,然后解方程求出,从而得到的长.
解:过点作于,过点作于,连接,如图,
( http: / / www.21cnjy.com / )
设,
,
,,
点为弧的中点,
,
,
,
线段绕点逆时针旋转得到线段,
,,
,,
,
在和△中
,
△,
,,
,
,解得,
.
故答案为4.
【点拨】本题考查了圆心角、弧、 ( http: / / www.21cnjy.com )弦的关系、旋转的性质,解题的关键是在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
13.18
【分析】
连接BE、CM,证明△ACE≌△BCF(SAS),推出∠MFB=,利用∠CFM=∠CBM=,得到C、M、B、F四点共圆,推出∠BCM=∠MFB=,从而求出AM=BM,得到;由CE∥BF推出,根据四边形ABFC的面积=求出结果.
解:连接BE、CM,
∵,,
∴,
∵,
∴∠ACE=∠BCF,
∵AC=BC,CE=CF,
∴△ACE≌△BCF(SAS),
∴∠CFB=∠CEA=,
∵∠CFE=,
∴∠MFB=,
∵∠CFM=∠CBM=,
∴C、M、B、F四点共圆,
∴∠BCM=∠MFB=,
∴∠CMB=,
∵AC=BC,
∴AM=BM,
∴;
∵∠ECF=∠CFB=,
∴∠ECF+∠CFB=,
∴CE∥BF,
∴,
∵四边形AMEC的面积=
∴四边形ABFC的面积==,
故答案为:18.
( http: / / www.21cnjy.com / ).
【点拨】此题考查等腰直角三角形的性质,等腰三 ( http: / / www.21cnjy.com )角形三线合一的性质,全等三角形的判定及性质,四点共圆的判定及性质,同底等高三角形面积的证明,这是一道较难的三角形综合题,熟练掌握各部分知识并综合运用是解题的关键.
14.5
【分析】
作出如图的辅助线,推出四边形OFBG是正方 ( http: / / www.21cnjy.com )形,设⊙O的半径为r,则OE=OD=OE=OG=BG=AM= r,ME=r -2,ON=r-1,证明Rt△OME≌Rt△OND,得到OM= ON=r-1,在Rt△OME中,利用勾股定理求解即可.
解:取DE的中点O,连接OF、OG,延长GO与AE的延长线相交于点M,过点D作DN⊥MG于点N,
( http: / / www.21cnjy.com / )
∵BC切⊙O于点G,∴CG⊥BG,
∵∠A=∠B=∠C=90°,
∴四边形ABGM、四边形GCDN和四边形OFBG都是矩形,
∵OF=OG,
∴四边形OFBG是正方形,
设⊙O的半径为r,则OE=OD=OE=OG=BG=AM= r,
∵AE=2,CD=1,
∴ME=r -2,ON=r-1,
在Rt△OME和Rt△OND中,,
∴Rt△OME≌Rt△OND,
∴OM= ON=r-1,
在Rt△OME中,OE2=ME2+OM2,
∴r2=( r -2)2+( r-1)2,
解得:r=1(舍去)或5,
故答案为:5.
【点拨】本题考查了切线的 ( http: / / www.21cnjy.com )性质,正方形的判定和性质,全等三角形的判定和性质,勾股中位线定理,解答本题的关键是明确题意,找出所求问题需要的条件.
15.
【分析】
(1)如图,延长交于点D,连接,根据,由圆周角定理得到,再根据已知,可得到,所以是的直径,再根据是的中线,由垂径定理的推论得到,最后利用勾股定理可求解;
(2)如图,连接、,由圆周角定理得到,然后利用勾股求出圆的半径,再根据点P是优弧上的动点,是的中线,结合三角形的三边关系定理可得到,,当为的直径时最大,这时可求得的最大值.
解:(1)如图,延长交于点D,连接,
∵,
∴,
又∵,
∴,
∴,
∴是的直径,
∵是的中线,
∴,
∴,
∴,
∴,
又∵,
∴,
解得.
故答案为:
( http: / / www.21cnjy.com / )
(2)如图,连接、,
∴,
∵,
∴,
∵,
∴,
解得:,
∵点P是优弧上的动点,是的中线,
∴,,
即,
当为的直径时最大,此时,
即
∴的最大值为.
故答案为:
( http: / / www.21cnjy.com / )
【点拨】本题考查的是圆与三角形的综合问题—动点问题,主要考查了圆周角定理、垂径定理的推论、勾股定理、三角形的三边关系定理等知识.发现当为的直径时可使取得最大值是解决问题的关键.
16.或
【分析】
作EF平行于MN,且与⊙O切,交x轴于点 ( http: / / www.21cnjy.com )E,交y轴于点F,设直线EF的解析式为y=x+b,由⊙O与直线EF相切结合三角形的面积即可得出关于b的含绝对值符号的一元一次方程,解方程即可求b值,从而得出点E的坐标,根据运动的相对性,即可得出结论.
解:作EF平行于MN,且与⊙O切,交x轴于点E,交y轴于点F,如图所示.
( http: / / www.21cnjy.com / )
设直线EF的解析式为y=x+b,即x-y+b=0,
∵EF与⊙O相切,且⊙O的半径为1,
∴,
解得:b=或b=,
∴直线EF的解析式为或,
∴点E的坐标为(,0)或(,0).
令y=x2中y=0,则x=2,
∴点M(2,0).
∵根据运动的相对性,且⊙O以每秒1个单位的速度向右作平移运动,
∴移动的时间为秒或秒.
故答案为:或.
【点拨】本题考查了直线与圆的位 ( http: / / www.21cnjy.com )置关系、一次函数图象上点的坐标特征以及平移的性质,解题的关键是求出点E、M的坐标.本题属于中档题,难度不大,解决该题时,巧妙的利用运动的相对性变移圆为移直线,降低了解题的难度.
17. 3:8
【分析】
(1)根据正六边形的性质特点求出的面积即可.
(2)根据第一问,利用和面积相等求解.
解:(1),
(2),
由题意是的中位线,
,
,
,
,
,
,
【点拨】本题考查正多边形与圆,三角形的面积,三角形的中位线定理,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
18.
【分析】
先判断出OB=OC=5,根据勾股 ( http: / / www.21cnjy.com )定理可得OA和AD的长,根据△ACD绕点A顺时针旋转60°得到△ABE,可得∠DAE=60°,AE=AD;再利用扇形面积公式即可求出结果.
解:∵B( 5,0),C(5,0),
∴OB=OC=5,AB=AC=BC=10,
∴,
∵D(11,0),
∴OD=11,
∴AD2=AO2+OD2=75+121=196,
∵△ACD绕点A顺时针旋转60°得到△ABE,
∴∠DAE=60°,AE=AD=,
∴图中阴影部分面积=S扇形DAE S扇形BAC
故答案为:16π
【点拨】本题考查了扇形面积的计算,旋转的性质,等边三角形的性质,勾股定理,坐标与图形变化 旋转,熟记扇形的面积公式是解答此题的关键.
19.(1)见分析;(2)2;(3)
【分析】
(1)利用圆周角定理得到∠ACB=90°,再证明OF⊥AC,然后根据垂径定理得到点D为的中点;
(2)证明OF为△ACB的中位线得到OF=BC=3,然后计算OD﹣OF即可;
(3)作C点关于AB的对 ( http: / / www.21cnjy.com )称点C′,C′D交AB于P,连接OC,如图,利用两点之间线段最短得到此时PC+PD的值最小,再计算出∠DOC′=120°,作OH⊥DC′于H,如图,然后根据等腰三角形的性质和含30度的直角三角形三边的关系求出DH,从而得到PC+PD的最小值.
解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴=,
即点D为的中点;
(2)解:∵OF⊥AC,
∴AF=CF,
而OA=OB,
∴OF为△ACB的中位线,
∴OF=BC=3,
∴DF=OD﹣OF=5﹣3=2;
(3)解:作C点关于AB的对称点C′,C′D交AB于P,连接OC,如图,
∵PC=PC′,
∴PD+PC=PD+PC′=DC′,
∴此时PC+PD的值最小,
∵=,
∴∠COD=∠AOD=80°,
∴∠BOC=20°,
∵点C和点C′关于AB对称,
∴∠C′OB=20°,
∴∠DOC′=120°,
作OH⊥DC′于H,如图,
则∠ODH=30°,
则C′H=DH,
在Rt△OHD中,OH=OD=,
∴DH=OH=,
∴DC′=2DH=,
∴PC+PD的最小值为.
( http: / / www.21cnjy.com / )
【点拨】本题考查了圆周角定理:在同圆 ( http: / / www.21cnjy.com )或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.
20.(1)为等腰直角三角形,详见分析(2)
【分析】
(1)由角平分线的定义、结合等量代换可得,即;然后再根据直径所对的圆周角为90°即可解答;
(2)如图:连接,,,交于点.先说明垂直平分.进而求得BD、OD、OB的长,设,则.然后根据勾股定理列出关于t的方程求解即可.
(1)解:为等腰直角三角形,证明如下:
证明:∵平分,平分,
∴,.
∵,,
∴.
∴.
∵为直径,
∴.
∴是等腰直角三角形.
(2)解:如图:连接,,,交于点.
∵,
∴.
∵,
∴垂直平分.
∵是等腰直角三角形,,
∴.
∵,
∴.
设,则.
在和中,.解得,.
∴.
∴.
( http: / / www.21cnjy.com / )
【点拨】本题主要考查了角平分线的定义、等腰三 ( http: / / www.21cnjy.com )角形的判定与性质、勾股定理的应用、垂直平分线的判定与性质、圆的性质等知识点,灵活运用相关知识成为解答本题的关键.2-1-c-n-j-y
21.(1)见详解;(2)
【分析】
(1)连接AD,根据弦、弧之间的关系证明DB=DE,证明△AMD≌△ABD,得到DM=BD,得到答案.
(2)连接OD,根据已知和切线的性质证明△OCD为等腰直角三角形,得到∠DOC=45°,根据S阴影=S△OCD-S扇OBD计算即可;
解:(1)如图,连接AD,
( http: / / www.21cnjy.com / )
∵AB是⊙O直径,
∴∠ADB=∠ADM=90°,
又∵,
∴ED=BD,∠MAD=∠BAD,
在△AMD和△ABD中,
,
∴△AMD≌△ABD,
∴DM=BD,
∴DE=DM;
(2)如上图,连接OD,
∵CD是⊙O切线,
∴OD⊥CD,
∵OA=CD=,OA=OD,
∴OD=CD=,
∴△OCD为等腰直角三角形,
∴∠DOC=∠C=45°,
∴S阴影=S△OCDS扇OBD=;
【点拨】本题考查的是切线的性质、弦、弧之间的关系、扇形面积的计算,掌握切线的性质定理和扇形的面积公式是解题的关键,注意辅助线的作法.
22.(1)∠A=48°;(2)∠A=90°.
【分析】
(1)先由题意得∠ADC=∠ABC, ( http: / / www.21cnjy.com )再据圆内接四边形性质得∠ADC+∠ABC=180°,得∠ABM=90°,由直角三角形两锐角互余可求出∠A度数;
(2)先证∠MDC+∠NBC=180°,再证∠MCD+∠NCB=180°-(α+β),再证∠BCD+∠NCM==180°+(α+β),再证∠BCD=90°+,最后由∠A+∠BCD=180°,可得∠A=90°.21世纪教育网版权所有
解:(1)在△CDM与△CBN中,∵∠M=∠N=42°,∠MCD=∠NCB,
∴∠CDM=∠CBN,
∴180°-∠CDM=180°-∠CBN,即∠ADC=∠ABC,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°;
∵∠M =42°,
∴∠A=90°-∠M=48°;
(2)∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠MDC+∠NBC=180°,
∵∠M+∠MDC+∠MCD=180°,∠N+∠NCB+∠NBC=180°,
∴∠M+∠N+∠MCD+∠NCB=180°,
又,
∴∠MCD+∠NCB=180°-(α+β),
∴∠BCD+∠NCM=360°-(∠MCD+∠NCB)=180°+(α+β),
∵∠BCD=∠NCM,
∴∠BCD=90°+,
∵∠A+∠BCD=180°,
∴∠A=90°-;
【点拨】此题考查:1.三角形内角和定理;2.圆内接四边形定理.其关键是运用相关定理结合图形对角进行运算.2·1·c·n·j·y
23.(1)见分析(2)①5;②
【分析】
(1)首先根据圆周角定理可得,由切线的性质可得,再根据平行线的性质即可证得,据此即可证得结论;21*cnjy*com
(2)①根据菱形性质可得OM= OA=M ( http: / / www.21cnjy.com )B= 5,即可求得AB,再根据勾股定理即可求得;②首先可证得△ODC是等腰直角三角形,再根据勾股定理及三角形的面积,即可求解.
(1)证明:∵AB是的直径,
,
,
∵CD是的切线,
,
,
又,
,
,
;
(2)解:①若四边形OCBM为菱形,
则OM=OA=MB =5,
∵AB是⊙O的直径,
∴,
∵OA=OB,
∴AB=2OA=10,
∴
当时,四边形OCBM为菱形;
故答案为:;
②如图所示:
( http: / / www.21cnjy.com / )
∵,OB=5,
∴,
∵CD是的切线,
∴,
∵OC=OB=5,
∴,
∴△ODC是等腰直角三角形,
∴,
又,
∴,
∵OM=OB,
∴,
∴,△OBM是等腰直角三角形,
在直角△ODM中,根据勾股定理可得,
根据△ODM的面积可得ON DM=OM OD,
,
故答案为:.
【点拨】此题主要考查了圆周角定理,圆的切线 ( http: / / www.21cnjy.com )的性质,平行线的性质与判定,菱形的性质,勾股定理,等腰直角三角形的判定与性质,熟练掌握和运用各图形的性质和判定是解决本题的关键.
24.(1)8(2)①;②最大值为,面积为
【分析】
(1)根据旋转的性质及全等三角形的性质可得答案;
(2)①将△ADC绕点C逆时针旋转60°,得到△BHC,根据等腰三角形的性质及面积公式可得答案;
②作点D关于直线AC的对 ( http: / / www.21cnjy.com )称点E,作点D关于BC的对称点F,当点E、M、N、F四点共线时,△DMN的周长最小,则连接EF交AC于点M,交BC于N,连接CE,CF,DE,DF,作CP⊥EF于P,由对称性质、勾股定理、最值问题可得答案.
解:(1)∵AB是直径,
∴∠ACB=90°,
∵△ACD旋转得到△BCE,
∴△ACD≌△BCE,
∴CD=CE=4,∠ACD=∠BCE,
∴∠DCE=∠DCB+∠BCE=∠DCB+∠ACD=90°,
∴S四边形ADBC=S△ACD+S△BCD=S△BCE+S△BCD=S△DCE=×DC×CE=×4×4=8.www.21-cn-jy.com
(2)①将△ADC绕点C逆时针旋转60°,得到△BHC,如图所示:
( http: / / www.21cnjy.com / )
∴CD=CH,∠DAC=∠HBC,
∵四边形ACBD是圆内接四边形,
∴∠DAC+∠DBC=180°,∠DBC+∠HBC=180°,
∴点D,B,H三点共线,
∵DC=CH,
∴∠CDH=60°,
∴△DCH是等腰三角形,
∴S四边形ADBC=S△ACD+S△BDC=S△CDH=,
∴;
②如图,作点关于直线的对称点,作点关于的对称点,
( http: / / www.21cnjy.com / )
点、关于直线对称,
,同理,,
,
当点、、、四点共线时,的周长最小,则连接交于点,交于,连接,,,,作于,
的周长最小值为,
点、关于直线对称,
,,
点、关于直线对称,
,,
,,
,,,
,,
,,
,
当有最大值时,有最大值,即有最大值,
为的弦,
为直径时,有最大值4,
的最大值为,
此时,.
【点拨】本题考查的是圆的综合运用,涉及到圆的有关性质、最值问题,掌握其性质定理是解决此题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
第24章 圆(培优篇)
一、单选题(本大题共10小题,每小题3分,共30分)
1.如图,PQ是半⊙O的直径,两 ( http: / / www.21cnjy.com )正方形彼此相邻且内接于半圆,E是CD中点,若小正方形的边长为4cm,则该半圆的直径PQ的长为( )
( http: / / www.21cnjy.com / )
A.cm B.cm C.cm D.cm
2.已知⊙O的直径CD=100cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=96cm,则AC的长为( )21cnjy.com
A.36cm或64cm B.60cm或80cm C.80cm D.60cm
3.如图,在半圆中,直径,是半圆上一点,将弧沿弦折叠交于,点是弧的中点.连接,则的最小值为( )
( http: / / www.21cnjy.com / )
A. B. C. D.
4.在平面直角坐标系中,已知点A(0,1),B(0,﹣5),若在x轴正半轴上有一点C,使∠ACB=30°,则点C的横坐标是( )21教育网
A.34 B.12 C.6+3 D.6
5.如图,⊙O的半径为1,点A、B、C、D ( http: / / www.21cnjy.com )在⊙O上,且四边形ABCD是矩形,点P是劣弧AD上一动点,PB、PC分别与AD相交于点E、点F.当PA=AB且AE=EF=FD时,AE的长度为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A. B. C. D.
6.如图,由5个边长为1的小正方形组成的“L”形,圆O经过其顶点A、B、C,则圆O的半径为( )
( http: / / www.21cnjy.com / )
A.5 B. C. D.
7.如图,△ABC的内切圆⊙O与AB,BC,AC相切于点D,E,F,已知AB=6,AC=5,BC=7,则DE的长是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
8.如图,AD是⊙O的直径,PA,PB分别切⊙O于点A,B,弦BC∥AD.当的度数为126°时,则∠P的度数为( )
( http: / / www.21cnjy.com / )
A.54° B.55° C.63° D.64°
9.如图,圆O是△ABC的外接圆,连接OA、OC,∠OAC=20°,则∠ABC的度数为( )
( http: / / www.21cnjy.com / )
A.140° B.110° C.70° D.40°
10.如图,AB为⊙O直径,且AB=4.点C为半圆上一动点(不与A,B重合),D为弧CB上一点,点E在AD上,且CD=BD=DE.则CE的最大值为( )
( http: / / www.21cnjy.com / )
A.4﹣4 B.2﹣ C.8﹣4 D.4﹣2
2、填空题(本大题共8小题,每小题4分,共32分)
11.如图,在半径为3的中,B是劣弧AC的中点,连接AB并延长到D,使,连接AC、BC、CD,如果,那么CD等于______.
( http: / / www.21cnjy.com / )
12.如图,扇形OAB中,∠AOB=60°,OA=4+8,点E为弧AB的中点,C为半径OA上一点,将线段CE绕点C逆时针旋转90°得到线段CE′,若点E′恰好落在半径OB上,则OE′=_____.21·cn·jy·com
( http: / / www.21cnjy.com / )
13.如图,中,,,点D是边BC上任意一点,连结AD,过点C作 于点E,过点C作,且,连结FE并延长交AB于点M,连结BF.若四边形AMEC的面积是8,,则四边形ABFC的面积是________.
( http: / / www.21cnjy.com / )
14.如图,在五边形AECDE中 ( http: / / www.21cnjy.com ),∠A=∠B=∠C=90°,AE=2,CD=1,以DE为直径的半圆分别与AB、BC相切于点F、G,则DE的长为______.
( http: / / www.21cnjy.com / )
15.如图,是的弦,,点P是优弧上的动点,,连接、,是的中线,(1)若,则____________;(2)的最大值=______________.
( http: / / www.21cnjy.com / )
16.如图所示,直线与x轴、y轴分别交于点M,N,的半径为1,将以每秒1个单位的速度向右作平移运动,当移动_________秒时,直线恰好与相切.
( http: / / www.21cnjy.com / )
17.如图,六边形是正六边形,边长为1,点P是边的中点,则______,若、分别与交于点M,N,则的值为_______.
( http: / / www.21cnjy.com / )
18.如图,在平面直角坐标系 ( http: / / www.21cnjy.com )中,等边△ABC的顶点A在y轴的正半轴上,B(﹣5,0),C(5,0),点D(11,0),将△ACD绕点A顺时针旋转60°得到△ABE,则线段CD转过区域的面积为________.
( http: / / www.21cnjy.com / )
三、解答题(本大题共6小题,共60分)
19.(8分)如图,是的直径,点、是上的点,且,分别与、相交于点、.
(1)求证:点为的中点;
(2)若,,求的长;
(3)若的半径为,,点是线段上任意一点,试求出的最小值.
( http: / / www.21cnjy.com / )
20.(8分)如图,以为直径的经过的顶点,,分别平分和,的延长线交于点,连接.
(1) 判断的形状,并证明你的结论;
(2) 若,,求的长.
( http: / / www.21cnjy.com / )
21.(10分)如图,AB是⊙O的直径,,连接DE、DB,延长AE交BD的延长线于点M,过点D作⊙O的切线交AB的延长线于点C.
(1)求证:DE=DM;
(2)若OA=CD=2,求阴影部分的面积.
( http: / / www.21cnjy.com / )
22.(10分)如图,的内接四边形ABCD两组对边的延长线分别交于点M,N.
(1)当∠M=∠N=42°时,求∠A的度数;
(2)若,且,请你用含有、的代数式表示∠A的度数.
( http: / / www.21cnjy.com / )
23.(10分)如图,以AB为直径的上有一动点C,的切线CD交AB的延长线于点D,过点B作交于点M,连接AM,OM,BC.
(1) 求证:
(2) 若,填空:
① 当AM= 时,四边形OCBM为菱形;
② 连接MD,过点O作于点N,若 ,则ON= .
( http: / / www.21cnjy.com / )
24.(12分)已知为的外接圆,,点是劣弧上一点(不与点,重合),连接,,.
(1)如图1,若是直径,将绕点逆时针旋转得到.若,求四边形的面积;
(2)如图2,若,半径为2,设线段的长为.四边形的面积为.
①求与的函数关系式;
②若点,分别在线段,上运动(不含端点),经过探究发现,点运动到每一个确定的位置.的周长有最小值,随着点的运动,的值会发生变化.求所有值中的最大值,并求此时四边形的面积.
( http: / / www.21cnjy.com / )
参考答案
1.D
【分析】
连接半径OB、OC、OF,可通过HL证明,得到OD=,最后运用勾股定理求解即可.
( http: / / www.21cnjy.com / )
解:如图,连接半径OB、OC、OF,则OB=OC=OF,
在正方形ABCD中,AB=CD,
(HL),
∴OA=OD,OD=,
E是CD中点,小正方形的边长为4cm,
∴DE=4cm,CD=8cm,OD=4cm,
,
∴该半圆的直径为2OC=cm.
故选:D.
【点拨】本题考查了全等三角形、勾股定理,属于综合题,能够熟练掌握各个知识点,并运用数形结合的思想是解题的关键.21·世纪*教育网
2.B
【分析】
分两种情况讨论,根据题意画出图形,根据垂径定理求出AM的长,连接OA,由勾股定理求出OM的长,进而可得出结论.【来源:21cnj*y.co*m】
解:连接AC,AO,
∵⊙O的直径CD=100cm,AB⊥CD,AB=96cm,
∴AM=AB=×96=48(cm),OD=OC=50(cm),
如图1,∵OA=50cm,AM=48cm,CD⊥AB,
∴OM===14(cm),
∴CM=OC+OM=50+14=64(cm),
∴AC===80(cm);
如图2,同理可得,OM=14cm,
∵OC=50cm,
∴MC==36(cm),
在Rt△AMC中,AC==60(cm);
综上所述,AC的长为80cm或60cm,
故选:B.
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
【点拨】本题考查的是垂径定理、勾股定理的应用,根据题意画出图形、利用垂径定理和勾股定理求解是解答此题的关键.21教育名师原创作品
3.D
【分析】
把弧AEC的圆补全为⊙F,可知点F与点O关于AC对称,求出∠F=90°,CE长,OE的最小值为EC-OC.
解:把弧AEC的圆补全为⊙F,可知点F与点O关于AC对称,半径为2,
∴∠FCA=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠FCA=∠CAO,
∴CF∥AB,
∵是弧的中点,
∴FE⊥AB,
∴∠F=∠BGE=90°,
∵FC=FE=2,
∴EC=,
∵OE≥EC-OC
即OE≥-2,
的最小值为,
故选:D.
( http: / / www.21cnjy.com / )
【点拨】本题考查了轴对称、垂径定理、勾股定理和圆的有关知识,解题关键是通过作辅助线,根据三角形三边关系确定OE的取值范围.
4.A
【分析】
如图,作的外接圆 连接 过作轴于 作轴于 则四边形是矩形,再证明是等边三角形,再分别求解即可得到答案.
解:如图,作的外接圆 连接 过作轴于 作轴于 则四边形是矩形,
( http: / / www.21cnjy.com / )
是等边三角形,
故选:
【点拨】本题考查的是坐标与图形, ( http: / / www.21cnjy.com )三角形的外接圆的性质,圆周角定理,等边三角形的判定与性质,矩形的判定与性质,勾股定理分应用,灵活应用以上知识解题是解题的关键.
5.A
【分析】
作辅助线,构建矩形的对角线,根据等边对 ( http: / / www.21cnjy.com )等角得∠ABP=∠APB,由同弧所对的圆周角相等可得∠ACB=∠ACP,根据矩形的四个角都是直角得∠ABC=90°,AE=EF=FD得FC=2FD,∠DCF=30°,得出∠ACB=30°,求出BC的长,则可得AD的长,再三等分即可.21*cnjy*com
解:连接AC、BD,
( http: / / www.21cnjy.com / )
∵PA=AB,
∴∠ABP=∠APB,
∵∠ABP=∠ACP,∠APB=∠ACB,
∴∠ACB=∠ACP,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠ACP=∠DAC,
∴AF=CF,
∵AE=EF=FD,
∴AF=DE=CF,则FC=2FD,
设FD=x,则FC=AF=2x,
∵四边形ABCD为矩形,
∴AD=BC,∠ABC=∠ADC=∠BCD=90°,
∴AC为⊙O的直径,
在Rt△DFC中,FC=2FD,
∴∠DCF=30°,
∴∠ACB=∠ACP=30°,
∵⊙O的半径为1,
∴AC=2,
∴AB=1,BC,
∴AD=BC,
∵AE=EF=FD,
∴AE.
故选:A.
【点拨】本题是有关圆的计算题,考查了矩形 ( http: / / www.21cnjy.com ),含30°的直角三角形的性质、等腰三角形的性质及圆周角、圆心角、弦、弧之间的关系,熟练掌握矩形的四个角都是直角,对角线相等且平分;在同圆或等圆中,同弧或等弧所对的圆周角相等.
6.D
【分析】
取AB的中点E,作,取圆心O,连接OB、OC,根据圆的性质,再结合勾股定理即可求解;
解:取AB的中点E,作,取圆心O,连接OB、OC,
( http: / / www.21cnjy.com / )
则
∵
设
解得:
∴
故选:D
【点拨】本题主要考查圆的性质、勾股定理,掌握相关知识并正确作出辅助线是解题的关键.
7.D
【分析】
连接、、,交于,作交BC于点G,利用 ,求出,进一步可得,求出,设⊙的半径为,利用,求出,求出,进一求出,再证明OB垂直平分,利用面积法可得,求得HE长即可求得答案.【来源:21·世纪·教育·网】
解:连接、、,交于,作交BC于点G,如图,
( http: / / www.21cnjy.com / )
∵AB=6,AC=5,BC=7,
∴,即,解得:,
∴,
∴,
设内切圆的半径为r,
则,解得:,
的内切圆⊙与,,分别相切于点,,,
∴∠ODB=∠OEB=90°,
又∵OD=OE, OB=OB,
∴,
∴BD=BE,
同理, CE=CF,AD=AF,
∵BE+CE=BC=7,
∴BD+BE+CE+CF=14,
∴2AD=(6+5+7)-14=4,即AD=2,
∴,
∴,
,,
垂直平分,
,,
,
,
,
故选:D.
【点拨】本题考查了三角形的内切圆性质,全等三角形的性质与判定,勾股定理,面积法等,正确添加辅助线,灵活运用相关知识是解题的关键.
8.A
【分析】
根据弧与圆心角的关系,可得,继而可得,根据平行线的性质以及同弧所对的圆周角相等,圆周角定理可得,根据领补角相等可得,根据切线长的性质以及切线的性质求得,进而求得,即可求得.【版权所有:21教育】
解:如图,连接,,,
( http: / / www.21cnjy.com / )
的度数为126°,
.
,
.
,
.
,
,,
.
,是⊙的切线,
,,,
.
故选A.
【点拨】本题考查了弧与圆心角的关系,平行线的性质,圆周角定理,同弧所对的圆周角相等,切线的性质,切线长定理,综合运用以上知识是解题的关键.
9.B
【分析】
根据OA=OC得到∠OAC=∠ ( http: / / www.21cnjy.com )OCA=20°,进而得到∠AOC=140°,在优弧AC上任取一点D,得到∠ADC=70°,然后根据内接四边形的性质即可求解.
解:∵OA=OC,∠OAC=20°
∴∠OAC=∠OCA=20°,
∴∠AOC=180°﹣20°×2=140°,
在优弧AC上任取一点D,连接AD、CD,如下图所示,
( http: / / www.21cnjy.com / )
∴∠ADC=70°
∴根据内接四边形的性质∠ABC=180°-70°=110°
故选:B.
【点拨】本题主要考查了等腰三角形的性质,圆周角定理,内接四边形的性质,作出辅助线是本题的关键.
10.A
【分析】
设,利用等弦对等弧,等弧所对的圆周角相等,等边对等角,三角形的外角的性质,通过角度的变换求得,确定的位置,进而证明,得到的运动轨迹是以点为圆心,4为半径的圆弧,进而根据直径是最长的弦求解即可.【出处:21教育名师】
解:延长,交于点,连接,OF
( http: / / www.21cnjy.com / )
设
CD=BD
为直径
在以点为圆心,4为半径的圆弧上运动,
,当为的直径时,取得最大值,最大值为
故选A
【点拨】本题考查了等弧所对的圆周角相等,弦与弧之间关系,找到点的运动轨迹,理解直径是最长的弦是解题的关键.
11.
【分析】
如图,连OA,OB.利用垂径定理和勾股定理求BE,利用中位线定理求CD.
解:如图,连OA,OB,
( http: / / www.21cnjy.com / )
∵B是弧AC的中点,AB=BC=BD,
∴△ACD是直角三角形,∠ACD=90°,
由垂径定理知,OB⊥AC,点E是AC的中点,
设,则,
由勾股定理知,, ,
∴,
∵AB=2,AO=BO=3,
∴,
解得, ,
即
∵∠AEB=∠ACD=90°,
∴BE∥CD,
∵点B是AD的中点,所以BE是△ACD的中位线,所以CD=2BE= .
故答案为:
【点拨】本题利用了垂径定理,勾股定理求解
12.
【分析】
过点作于,过点作于,连接,如图,设,利用得到,,再利用点为弧的中点得到,所以,,接着证明△,则,,则可列方程,然后解方程求出,从而得到的长.
解:过点作于,过点作于,连接,如图,
( http: / / www.21cnjy.com / )
设,
,
,,
点为弧的中点,
,
,
,
线段绕点逆时针旋转得到线段,
,,
,,
,
在和△中
,
△,
,,
,
,解得,
.
故答案为4.
【点拨】本题考查了圆心角、弧、 ( http: / / www.21cnjy.com )弦的关系、旋转的性质,解题的关键是在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
13.18
【分析】
连接BE、CM,证明△ACE≌△BCF(SAS),推出∠MFB=,利用∠CFM=∠CBM=,得到C、M、B、F四点共圆,推出∠BCM=∠MFB=,从而求出AM=BM,得到;由CE∥BF推出,根据四边形ABFC的面积=求出结果.
解:连接BE、CM,
∵,,
∴,
∵,
∴∠ACE=∠BCF,
∵AC=BC,CE=CF,
∴△ACE≌△BCF(SAS),
∴∠CFB=∠CEA=,
∵∠CFE=,
∴∠MFB=,
∵∠CFM=∠CBM=,
∴C、M、B、F四点共圆,
∴∠BCM=∠MFB=,
∴∠CMB=,
∵AC=BC,
∴AM=BM,
∴;
∵∠ECF=∠CFB=,
∴∠ECF+∠CFB=,
∴CE∥BF,
∴,
∵四边形AMEC的面积=
∴四边形ABFC的面积==,
故答案为:18.
( http: / / www.21cnjy.com / ).
【点拨】此题考查等腰直角三角形的性质,等腰三 ( http: / / www.21cnjy.com )角形三线合一的性质,全等三角形的判定及性质,四点共圆的判定及性质,同底等高三角形面积的证明,这是一道较难的三角形综合题,熟练掌握各部分知识并综合运用是解题的关键.
14.5
【分析】
作出如图的辅助线,推出四边形OFBG是正方 ( http: / / www.21cnjy.com )形,设⊙O的半径为r,则OE=OD=OE=OG=BG=AM= r,ME=r -2,ON=r-1,证明Rt△OME≌Rt△OND,得到OM= ON=r-1,在Rt△OME中,利用勾股定理求解即可.
解:取DE的中点O,连接OF、OG,延长GO与AE的延长线相交于点M,过点D作DN⊥MG于点N,
( http: / / www.21cnjy.com / )
∵BC切⊙O于点G,∴CG⊥BG,
∵∠A=∠B=∠C=90°,
∴四边形ABGM、四边形GCDN和四边形OFBG都是矩形,
∵OF=OG,
∴四边形OFBG是正方形,
设⊙O的半径为r,则OE=OD=OE=OG=BG=AM= r,
∵AE=2,CD=1,
∴ME=r -2,ON=r-1,
在Rt△OME和Rt△OND中,,
∴Rt△OME≌Rt△OND,
∴OM= ON=r-1,
在Rt△OME中,OE2=ME2+OM2,
∴r2=( r -2)2+( r-1)2,
解得:r=1(舍去)或5,
故答案为:5.
【点拨】本题考查了切线的 ( http: / / www.21cnjy.com )性质,正方形的判定和性质,全等三角形的判定和性质,勾股中位线定理,解答本题的关键是明确题意,找出所求问题需要的条件.
15.
【分析】
(1)如图,延长交于点D,连接,根据,由圆周角定理得到,再根据已知,可得到,所以是的直径,再根据是的中线,由垂径定理的推论得到,最后利用勾股定理可求解;
(2)如图,连接、,由圆周角定理得到,然后利用勾股求出圆的半径,再根据点P是优弧上的动点,是的中线,结合三角形的三边关系定理可得到,,当为的直径时最大,这时可求得的最大值.
解:(1)如图,延长交于点D,连接,
∵,
∴,
又∵,
∴,
∴,
∴是的直径,
∵是的中线,
∴,
∴,
∴,
∴,
又∵,
∴,
解得.
故答案为:
( http: / / www.21cnjy.com / )
(2)如图,连接、,
∴,
∵,
∴,
∵,
∴,
解得:,
∵点P是优弧上的动点,是的中线,
∴,,
即,
当为的直径时最大,此时,
即
∴的最大值为.
故答案为:
( http: / / www.21cnjy.com / )
【点拨】本题考查的是圆与三角形的综合问题—动点问题,主要考查了圆周角定理、垂径定理的推论、勾股定理、三角形的三边关系定理等知识.发现当为的直径时可使取得最大值是解决问题的关键.
16.或
【分析】
作EF平行于MN,且与⊙O切,交x轴于点 ( http: / / www.21cnjy.com )E,交y轴于点F,设直线EF的解析式为y=x+b,由⊙O与直线EF相切结合三角形的面积即可得出关于b的含绝对值符号的一元一次方程,解方程即可求b值,从而得出点E的坐标,根据运动的相对性,即可得出结论.
解:作EF平行于MN,且与⊙O切,交x轴于点E,交y轴于点F,如图所示.
( http: / / www.21cnjy.com / )
设直线EF的解析式为y=x+b,即x-y+b=0,
∵EF与⊙O相切,且⊙O的半径为1,
∴,
解得:b=或b=,
∴直线EF的解析式为或,
∴点E的坐标为(,0)或(,0).
令y=x2中y=0,则x=2,
∴点M(2,0).
∵根据运动的相对性,且⊙O以每秒1个单位的速度向右作平移运动,
∴移动的时间为秒或秒.
故答案为:或.
【点拨】本题考查了直线与圆的位 ( http: / / www.21cnjy.com )置关系、一次函数图象上点的坐标特征以及平移的性质,解题的关键是求出点E、M的坐标.本题属于中档题,难度不大,解决该题时,巧妙的利用运动的相对性变移圆为移直线,降低了解题的难度.
17. 3:8
【分析】
(1)根据正六边形的性质特点求出的面积即可.
(2)根据第一问,利用和面积相等求解.
解:(1),
(2),
由题意是的中位线,
,
,
,
,
,
,
【点拨】本题考查正多边形与圆,三角形的面积,三角形的中位线定理,等腰三角形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
18.
【分析】
先判断出OB=OC=5,根据勾股 ( http: / / www.21cnjy.com )定理可得OA和AD的长,根据△ACD绕点A顺时针旋转60°得到△ABE,可得∠DAE=60°,AE=AD;再利用扇形面积公式即可求出结果.
解:∵B( 5,0),C(5,0),
∴OB=OC=5,AB=AC=BC=10,
∴,
∵D(11,0),
∴OD=11,
∴AD2=AO2+OD2=75+121=196,
∵△ACD绕点A顺时针旋转60°得到△ABE,
∴∠DAE=60°,AE=AD=,
∴图中阴影部分面积=S扇形DAE S扇形BAC
故答案为:16π
【点拨】本题考查了扇形面积的计算,旋转的性质,等边三角形的性质,勾股定理,坐标与图形变化 旋转,熟记扇形的面积公式是解答此题的关键.
19.(1)见分析;(2)2;(3)
【分析】
(1)利用圆周角定理得到∠ACB=90°,再证明OF⊥AC,然后根据垂径定理得到点D为的中点;
(2)证明OF为△ACB的中位线得到OF=BC=3,然后计算OD﹣OF即可;
(3)作C点关于AB的对 ( http: / / www.21cnjy.com )称点C′,C′D交AB于P,连接OC,如图,利用两点之间线段最短得到此时PC+PD的值最小,再计算出∠DOC′=120°,作OH⊥DC′于H,如图,然后根据等腰三角形的性质和含30度的直角三角形三边的关系求出DH,从而得到PC+PD的最小值.
解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴=,
即点D为的中点;
(2)解:∵OF⊥AC,
∴AF=CF,
而OA=OB,
∴OF为△ACB的中位线,
∴OF=BC=3,
∴DF=OD﹣OF=5﹣3=2;
(3)解:作C点关于AB的对称点C′,C′D交AB于P,连接OC,如图,
∵PC=PC′,
∴PD+PC=PD+PC′=DC′,
∴此时PC+PD的值最小,
∵=,
∴∠COD=∠AOD=80°,
∴∠BOC=20°,
∵点C和点C′关于AB对称,
∴∠C′OB=20°,
∴∠DOC′=120°,
作OH⊥DC′于H,如图,
则∠ODH=30°,
则C′H=DH,
在Rt△OHD中,OH=OD=,
∴DH=OH=,
∴DC′=2DH=,
∴PC+PD的最小值为.
( http: / / www.21cnjy.com / )
【点拨】本题考查了圆周角定理:在同圆 ( http: / / www.21cnjy.com )或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理.
20.(1)为等腰直角三角形,详见分析(2)
【分析】
(1)由角平分线的定义、结合等量代换可得,即;然后再根据直径所对的圆周角为90°即可解答;
(2)如图:连接,,,交于点.先说明垂直平分.进而求得BD、OD、OB的长,设,则.然后根据勾股定理列出关于t的方程求解即可.
(1)解:为等腰直角三角形,证明如下:
证明:∵平分,平分,
∴,.
∵,,
∴.
∴.
∵为直径,
∴.
∴是等腰直角三角形.
(2)解:如图:连接,,,交于点.
∵,
∴.
∵,
∴垂直平分.
∵是等腰直角三角形,,
∴.
∵,
∴.
设,则.
在和中,.解得,.
∴.
∴.
( http: / / www.21cnjy.com / )
【点拨】本题主要考查了角平分线的定义、等腰三 ( http: / / www.21cnjy.com )角形的判定与性质、勾股定理的应用、垂直平分线的判定与性质、圆的性质等知识点,灵活运用相关知识成为解答本题的关键.2-1-c-n-j-y
21.(1)见详解;(2)
【分析】
(1)连接AD,根据弦、弧之间的关系证明DB=DE,证明△AMD≌△ABD,得到DM=BD,得到答案.
(2)连接OD,根据已知和切线的性质证明△OCD为等腰直角三角形,得到∠DOC=45°,根据S阴影=S△OCD-S扇OBD计算即可;
解:(1)如图,连接AD,
( http: / / www.21cnjy.com / )
∵AB是⊙O直径,
∴∠ADB=∠ADM=90°,
又∵,
∴ED=BD,∠MAD=∠BAD,
在△AMD和△ABD中,
,
∴△AMD≌△ABD,
∴DM=BD,
∴DE=DM;
(2)如上图,连接OD,
∵CD是⊙O切线,
∴OD⊥CD,
∵OA=CD=,OA=OD,
∴OD=CD=,
∴△OCD为等腰直角三角形,
∴∠DOC=∠C=45°,
∴S阴影=S△OCDS扇OBD=;
【点拨】本题考查的是切线的性质、弦、弧之间的关系、扇形面积的计算,掌握切线的性质定理和扇形的面积公式是解题的关键,注意辅助线的作法.
22.(1)∠A=48°;(2)∠A=90°.
【分析】
(1)先由题意得∠ADC=∠ABC, ( http: / / www.21cnjy.com )再据圆内接四边形性质得∠ADC+∠ABC=180°,得∠ABM=90°,由直角三角形两锐角互余可求出∠A度数;
(2)先证∠MDC+∠NBC=180°,再证∠MCD+∠NCB=180°-(α+β),再证∠BCD+∠NCM==180°+(α+β),再证∠BCD=90°+,最后由∠A+∠BCD=180°,可得∠A=90°.21世纪教育网版权所有
解:(1)在△CDM与△CBN中,∵∠M=∠N=42°,∠MCD=∠NCB,
∴∠CDM=∠CBN,
∴180°-∠CDM=180°-∠CBN,即∠ADC=∠ABC,
∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°;
∵∠M =42°,
∴∠A=90°-∠M=48°;
(2)∵四边形ABCD内接于⊙O,
∴∠ADC+∠ABC=180°,
∴∠MDC+∠NBC=180°,
∵∠M+∠MDC+∠MCD=180°,∠N+∠NCB+∠NBC=180°,
∴∠M+∠N+∠MCD+∠NCB=180°,
又,
∴∠MCD+∠NCB=180°-(α+β),
∴∠BCD+∠NCM=360°-(∠MCD+∠NCB)=180°+(α+β),
∵∠BCD=∠NCM,
∴∠BCD=90°+,
∵∠A+∠BCD=180°,
∴∠A=90°-;
【点拨】此题考查:1.三角形内角和定理;2.圆内接四边形定理.其关键是运用相关定理结合图形对角进行运算.2·1·c·n·j·y
23.(1)见分析(2)①5;②
【分析】
(1)首先根据圆周角定理可得,由切线的性质可得,再根据平行线的性质即可证得,据此即可证得结论;21*cnjy*com
(2)①根据菱形性质可得OM= OA=M ( http: / / www.21cnjy.com )B= 5,即可求得AB,再根据勾股定理即可求得;②首先可证得△ODC是等腰直角三角形,再根据勾股定理及三角形的面积,即可求解.
(1)证明:∵AB是的直径,
,
,
∵CD是的切线,
,
,
又,
,
,
;
(2)解:①若四边形OCBM为菱形,
则OM=OA=MB =5,
∵AB是⊙O的直径,
∴,
∵OA=OB,
∴AB=2OA=10,
∴
当时,四边形OCBM为菱形;
故答案为:;
②如图所示:
( http: / / www.21cnjy.com / )
∵,OB=5,
∴,
∵CD是的切线,
∴,
∵OC=OB=5,
∴,
∴△ODC是等腰直角三角形,
∴,
又,
∴,
∵OM=OB,
∴,
∴,△OBM是等腰直角三角形,
在直角△ODM中,根据勾股定理可得,
根据△ODM的面积可得ON DM=OM OD,
,
故答案为:.
【点拨】此题主要考查了圆周角定理,圆的切线 ( http: / / www.21cnjy.com )的性质,平行线的性质与判定,菱形的性质,勾股定理,等腰直角三角形的判定与性质,熟练掌握和运用各图形的性质和判定是解决本题的关键.
24.(1)8(2)①;②最大值为,面积为
【分析】
(1)根据旋转的性质及全等三角形的性质可得答案;
(2)①将△ADC绕点C逆时针旋转60°,得到△BHC,根据等腰三角形的性质及面积公式可得答案;
②作点D关于直线AC的对 ( http: / / www.21cnjy.com )称点E,作点D关于BC的对称点F,当点E、M、N、F四点共线时,△DMN的周长最小,则连接EF交AC于点M,交BC于N,连接CE,CF,DE,DF,作CP⊥EF于P,由对称性质、勾股定理、最值问题可得答案.
解:(1)∵AB是直径,
∴∠ACB=90°,
∵△ACD旋转得到△BCE,
∴△ACD≌△BCE,
∴CD=CE=4,∠ACD=∠BCE,
∴∠DCE=∠DCB+∠BCE=∠DCB+∠ACD=90°,
∴S四边形ADBC=S△ACD+S△BCD=S△BCE+S△BCD=S△DCE=×DC×CE=×4×4=8.www.21-cn-jy.com
(2)①将△ADC绕点C逆时针旋转60°,得到△BHC,如图所示:
( http: / / www.21cnjy.com / )
∴CD=CH,∠DAC=∠HBC,
∵四边形ACBD是圆内接四边形,
∴∠DAC+∠DBC=180°,∠DBC+∠HBC=180°,
∴点D,B,H三点共线,
∵DC=CH,
∴∠CDH=60°,
∴△DCH是等腰三角形,
∴S四边形ADBC=S△ACD+S△BDC=S△CDH=,
∴;
②如图,作点关于直线的对称点,作点关于的对称点,
( http: / / www.21cnjy.com / )
点、关于直线对称,
,同理,,
,
当点、、、四点共线时,的周长最小,则连接交于点,交于,连接,,,,作于,
的周长最小值为,
点、关于直线对称,
,,
点、关于直线对称,
,,
,,
,,,
,,
,,
,
当有最大值时,有最大值,即有最大值,
为的弦,
为直径时,有最大值4,
的最大值为,
此时,.
【点拨】本题考查的是圆的综合运用,涉及到圆的有关性质、最值问题,掌握其性质定理是解决此题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
