北师大版数学八年级上册 1.2一定是直角三角形吗 同步练习题 (含答案)
文档属性
| 名称 | 北师大版数学八年级上册 1.2一定是直角三角形吗 同步练习题 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 283.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 07:00:37 | ||
图片预览




文档简介
2022-2023学年北师大版八年级数学上册《1.2一定是直角三角形吗》同步练习题(附答案)
一.选择题
1.下列各组数是勾股数的一组是( )
A.7,24,25 B.32,42,52 C.1.5,2,2.5 D.3, 4, 7
2.下列各组数中不能作为直角三角形的三边长的是( )
A.3,4,5 B.2,3,4 C.7,24,25 D.9,12,15
3.如图,小正方形的边长均为1,A、B、C是小正方形的顶点,则∠ACB的度数是( )
A.30° B.45° C.60° D.90°
4.下列条件中,不能判定△ABC为直角三角形的是( )
A.c2=a2+b2 B.∠A+∠B=∠C
C.∠A:∠B:∠C=2:3:5 D.a=6,b=12,c=13
5.五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是( )
A. B.
C. D.
6.在△ABC中,BC2﹣AC2=AB2.若∠B=25°,则∠C=( )
A.20° B.35° C.65° D.75°
7.如图,在3×3的方格纸中,已知点A,B在方格顶点上(也称格点),若点C也是格点,且使得△ABC为直角三角形,则满足条件的C点有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
8.如图,以△ABC的三边向外作正方形,依次得到的正方形的面积为36,64,100,则这个三角形的面积是 .
9.如图,四边形ABCD中,AB⊥BC,AB=4,BC=3,AD=12,CD=13,则四边形ABCD的面积是 .
10.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
11.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2= .
12.如图,点A、B、C在正方形网格点上,则∠ABC+∠ACB= .
13.如图,AD是△ABC的中线,若AB=13,BC=10,AD=12,则AC= .
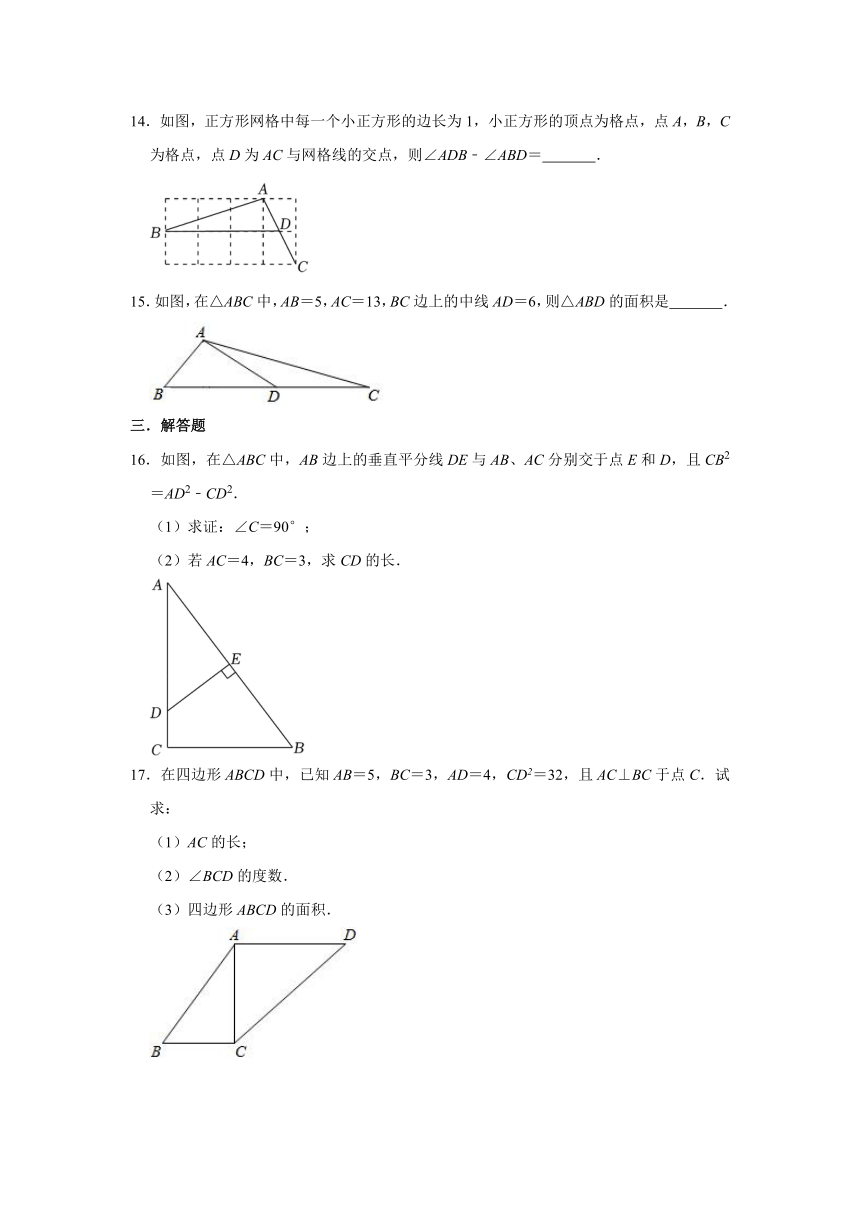
14.如图,正方形网格中每一个小正方形的边长为1,小正方形的顶点为格点,点A,B,C为格点,点D为AC与网格线的交点,则∠ADB﹣∠ABD= .
15.如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是 .
三.解答题
16.如图,在△ABC中,AB边上的垂直平分线DE与AB、AC分别交于点E和D,且CB2=AD2﹣CD2.
(1)求证:∠C=90°;
(2)若AC=4,BC=3,求CD的长.
17.在四边形ABCD中,已知AB=5,BC=3,AD=4,CD2=32,且AC⊥BC于点C.试求:
(1)AC的长;
(2)∠BCD的度数.
(3)四边形ABCD的面积.
18.如图,在△ABC中,AE=3,BE=5,AC=4,DE是BC的垂直平分线,交BC于点D,交AB于点E.求证:△ABC为直角三角形.
19.如图,在方格纸上的每个小正方形的边长都是1,点A,B,C,D都在正方形的顶点上.
(1)△ABC和△ACD都是直角三角形吗?为什么?
(2)由(1)能判定D,C,B三点在一条直线上吗?说明理由;
(3)求∠ADC的度数.
20.如图,在△ABC中,D是边BC的中点,E是边AC的中点,连接AD,BE.
(1)若CD=8,CE=6,AB=20,求证:∠C=90°;
(2)若∠C=90°,AD=13,AE=6,求△ABC的面积.
21.早在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫做“整数直角三角形”,那么这三个整数叫做一组“勾股数”.在一次“构造勾股数”的探究性学习中,老师给出了下表(其中m,n为正整数,且m>n):
m 2 3 3 4 4 …
n 1 1 2 1 2 …
a 22+12 32+12 32+22 42+12 42+22 …
b 4 6 12 8 16 …
c 22﹣12 32﹣12 32﹣22 42﹣12 42﹣22 …
(1)探究a,b,c与m,n之间的关系并用含m,n的代数式表示:a= ,b= ,c= .
(2)以a,b,c为边长的三角形是否一定为直角三角形?请说明理由.
参考答案
一.选择题
1.解:A、∵72+242=252,
∴7、24、25是一组勾股数,故本选项符合题意;
B、∵(32)2+(42)2≠(52)2,
∴32、42、52不是一组勾股数,故本选项不符合题意;
C、∵1.5和2.5不是正整数,
∴1.5、2、2.5不是一组勾股数,故本选项不符合题意;
D、∵3,4,7不能构成三角形,故本选项不符合题意;
故选:A.
2.解:A、32+42=52,符合勾股定理的逆定理,故本选项不符合题意;
B、22+32≠42,不符合勾股定理的逆定理,故本选项符合题意;
C、72+242=252,符合勾股定理的逆定理,故本选项不符合题意;
D、92+122=152,符合勾股定理的逆定理,故本选项不符合题意.
故选:B.
3.解:由图可知:
∴AB2+BC2=AC2,AB=BC,
∴△ABC为等腰直角三角形,∠ABC=90°,
∴∠ACB=45°.
故选:B.
4.解:A、∵c2=a2+b2,
∴能判定△ABC为直角三角形,
故A不符合题意;
B、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴能判定△ABC为直角三角形,
故B不符合题意;
C、∵∠A:∠B:∠C=2:3:5,∠A+∠B+∠C=180°,
∴∠C=180°×=90°,
∴能判定△ABC为直角三角形,
故C不符合题意;
D、∵a=6,b=12,c=13,
∴a2+b2=62+122=180,c2=132=169,
∴a2+b2≠c2,
∴不能判定△ABC为直角三角形,
故D符合题意;
故选:D.
5.解:∵82+152=172,92+122=152,
∴用长度为8,15,17和9,12,15的小木棒能分别摆成两个直角三角形,
故选:C.
6.解:∵BC2﹣AC2=AB2,
∴BC2=AC2+AB2,
∴△ABC是直角三角形,
∴∠A=90°,
∵∠B=25°,
∴∠C=90°﹣∠B=65°,
故选:C.
7.解:如图,分情况讨论:
①AB为直角△ABC斜边时,符合条件的格点C点有2个;
②AB为直角△ABC其中的一条直角边时,符合条件的格点C点有1个.
故共有3个点,
故选:C.
二.填空题
8.解:由题可得,36+64=100,
∴62+82=102,
∴△ABC是直角三角形,且∠ABC=90°,
又∵AB=6,BC=8,
∴△ABC的面积=AB×BC==24.
故答案为:24.
9.解:如图,连接AC,
在△ABC中,AB⊥BC,AB=4,BC=3,
∴AC=5.
在△ADC中,AD=12,CD=13,AC=5.
∵122+52=132,即AD2+AC2=CD2,
∴△ADC是直角三角形,且∠DAC=90°,
∴S四边形ABCD=S△ABC+S△ADC
=AB BC+AC AD
=×4×3+×5×12
=6+30
=36.
故答案为:36.
10.解:∵m为正整数,
∴2m为偶数,设其股是a,则弦为a+2,
根据勾股定理得,(2m)2+a2=(a+2)2,
解得a=m2﹣1,
∴弦是a+2=m2﹣1+2=m2+1,
故答案为:m2+1.
11.解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=∠ACB,∠ACF=∠ACD,即∠ECF=(∠ACB+∠ACD)=90°,
又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,
∴CM=EM=MF=5,EF=10,
由勾股定理可知CE2+CF2=EF2=100.
12.解:如图:延长BA到点D,连接CD,
由题意得:
AD2=22+12=5,
CD2=22+12=5,
AC2=12+32=10,
∴AD2+CD2=AC2,
∴△ACD是直角三角形,
∴∠ADC=90°,
∵AD=CD,
∴∠DAC=∠DCA=45°,
∵∠DAC是△ABC的一个外角,
∴∠DAC=∠ABC+∠ACB=45°,
故答案为:45°.
13.解:∵AD为△ABC的中线,BC=10,
∴BD=CD=BC=5,
∵AB=13,AD=12,
∴52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵CD=BD,
∴AC=AB=13.
故答案为:13.
14.解:如图:连接AE,BE,设AE与BD交于点F,
由题意得:
AB2=12+32=10,
AE2=12+22=5,
EB2=12+22=5,
∴AE=EB,BE2+AE2=AB2,
∴△ABE是等腰直角三角形,
∴∠BAE=45°,
∵BD∥EC,
∴∠ADB=∠ACE,∠AFD=∠AEC,
∵AE=AC,
∴∠AEC=∠ACE,
∴∠AFD=∠ADF,
∵∠AFD是△ABF的一个外角,
∴∠AFD﹣∠ABD=∠BAE=45°,
∴∠ADB﹣∠ABD=45°,
故答案为:45°.
15.解:延长AD到点E,使DE=AD=6,连接CE,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△CED中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=5,∠BAD=∠E,
∵AE=2AD=12,CE=5,AC=13,
∴CE2+AE2=AC2,
∴∠E=90°,
∴∠BAD=90°,
即△ABD为直角三角形,
∴△ABD的面积=AD AB=15,
故答案为:15.
三.解答题
16.(1)证明:连接BD,
∵AB边上的垂直平分线为DE,
∴AD=BD,
∵CB2=AD2﹣CD2,
∴CB2=BD2﹣CD2,
∴CB2+CD2=BD2,
∴∠C=90°;
(2)解:设CD=x,则AD=BD=4﹣x,
在Rt△BCD中,BD2﹣CD2=BC2,
∴(4﹣x)2﹣x2=32,
解得:x=,
∴CD的长为.
17.解:(1)∵AC⊥BC,
∴∠ACB=90°,
∵AB=5,BC=3,
∴AC=4,
∴AC的长为4;
(2)∵AC=4,AD=4,CD2=32,
∴AC2+AD2=42+42=32,CD2=32,
∴AC2+AD2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∵AC=AD=4,
∴∠ACD=∠D=45°,
∵∠ACB=90°,
∴∠BCD=∠ACB+∠ACD=135°,
∴∠BCD的度数为135°;
(3)由题意得:
四边形ABCD的面积=△ABC的面积+△ACD的面积
=AC CB+AD AC
=×4×3+×4×4
=6+8
=14,
∴四边形ABCD的面积为14.
18.证明:连接CE,
∵DE是BC的垂直平分线,
∴EC=BE=5,
在△AEC中,AE=3,EC=5,AC=4,
∵AC2+AE2=42+32=25,EC2=52=25,
∴AC2+AE2=EC2,
∴△AEC是直角三角形,
∴∠A=90°,
∴△ABC是直角三角形.
19.解:(1)△ABC不是直角三角形,△ACD是直角三角形,
理由:∵AD2=52+12=26,AC2+CD2=32+22+32+22=26,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴△ACD是直角三角形,
∵AC2+BC2=13+12+22=18,AB2=42=16,
∴AC2+BC2≠AB2,
∴△ABC不是直角三角形;
(2)D,C,B三点不在一条直线上,
理由:∵∠ACD=90°,∠ACB≠90°,
∴∠BCD≠180°,
∴D,C,B三点不在一条直线上;
(3)由(1)知,∠ACD=90°,
∵AC2=CD2=13,
∴△ACD是等腰直角三角形,
∴∠ADC=45°
20.(1)证明:∵D是边BC的中点,E是边AC的中点,CD=8,CE=6,
∴AC=2CE=12,BC=2CD=16,
∵AB=20,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,
∴∠C=90°;
(2)解:∵E是边AC的中点,AE=6,
∴AC=2AE=12.
在Rt△ACD中,∵∠C=90°,AC=12,AD=13,
∴CD=5,
∴BC=2CD=10,
∴△ABC的面积=AC BC=×12×10=60.
21.解:(1)观察得,a=m2+n2,b=2mn,c=m2﹣n2.
故答案为:m2+n2,2mn,m2﹣n2;
(2)以a,b,c为边长的三角形一定为直角三角形,理由如下:
∵a2=(m2+n2)2=m4+2m2n2+n4,
b2+c2=m4﹣2m2n2+n4+4m2n2=m4+2m2n2+n4,
∴a2=b2+c2,
∴以a,b,c为边长的三角形一定为直角三角形.
一.选择题
1.下列各组数是勾股数的一组是( )
A.7,24,25 B.32,42,52 C.1.5,2,2.5 D.3, 4, 7
2.下列各组数中不能作为直角三角形的三边长的是( )
A.3,4,5 B.2,3,4 C.7,24,25 D.9,12,15
3.如图,小正方形的边长均为1,A、B、C是小正方形的顶点,则∠ACB的度数是( )
A.30° B.45° C.60° D.90°
4.下列条件中,不能判定△ABC为直角三角形的是( )
A.c2=a2+b2 B.∠A+∠B=∠C
C.∠A:∠B:∠C=2:3:5 D.a=6,b=12,c=13
5.五根小木棒,其长度(单位:cm)分别为8,9,12,15,17,现将它们摆成两个直角三角形,其中正确的是( )
A. B.
C. D.
6.在△ABC中,BC2﹣AC2=AB2.若∠B=25°,则∠C=( )
A.20° B.35° C.65° D.75°
7.如图,在3×3的方格纸中,已知点A,B在方格顶点上(也称格点),若点C也是格点,且使得△ABC为直角三角形,则满足条件的C点有( )
A.1个 B.2个 C.3个 D.4个
二.填空题
8.如图,以△ABC的三边向外作正方形,依次得到的正方形的面积为36,64,100,则这个三角形的面积是 .
9.如图,四边形ABCD中,AB⊥BC,AB=4,BC=3,AD=12,CD=13,则四边形ABCD的面积是 .
10.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
11.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2= .
12.如图,点A、B、C在正方形网格点上,则∠ABC+∠ACB= .
13.如图,AD是△ABC的中线,若AB=13,BC=10,AD=12,则AC= .
14.如图,正方形网格中每一个小正方形的边长为1,小正方形的顶点为格点,点A,B,C为格点,点D为AC与网格线的交点,则∠ADB﹣∠ABD= .
15.如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是 .
三.解答题
16.如图,在△ABC中,AB边上的垂直平分线DE与AB、AC分别交于点E和D,且CB2=AD2﹣CD2.
(1)求证:∠C=90°;
(2)若AC=4,BC=3,求CD的长.
17.在四边形ABCD中,已知AB=5,BC=3,AD=4,CD2=32,且AC⊥BC于点C.试求:
(1)AC的长;
(2)∠BCD的度数.
(3)四边形ABCD的面积.
18.如图,在△ABC中,AE=3,BE=5,AC=4,DE是BC的垂直平分线,交BC于点D,交AB于点E.求证:△ABC为直角三角形.
19.如图,在方格纸上的每个小正方形的边长都是1,点A,B,C,D都在正方形的顶点上.
(1)△ABC和△ACD都是直角三角形吗?为什么?
(2)由(1)能判定D,C,B三点在一条直线上吗?说明理由;
(3)求∠ADC的度数.
20.如图,在△ABC中,D是边BC的中点,E是边AC的中点,连接AD,BE.
(1)若CD=8,CE=6,AB=20,求证:∠C=90°;
(2)若∠C=90°,AD=13,AE=6,求△ABC的面积.
21.早在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫做“整数直角三角形”,那么这三个整数叫做一组“勾股数”.在一次“构造勾股数”的探究性学习中,老师给出了下表(其中m,n为正整数,且m>n):
m 2 3 3 4 4 …
n 1 1 2 1 2 …
a 22+12 32+12 32+22 42+12 42+22 …
b 4 6 12 8 16 …
c 22﹣12 32﹣12 32﹣22 42﹣12 42﹣22 …
(1)探究a,b,c与m,n之间的关系并用含m,n的代数式表示:a= ,b= ,c= .
(2)以a,b,c为边长的三角形是否一定为直角三角形?请说明理由.
参考答案
一.选择题
1.解:A、∵72+242=252,
∴7、24、25是一组勾股数,故本选项符合题意;
B、∵(32)2+(42)2≠(52)2,
∴32、42、52不是一组勾股数,故本选项不符合题意;
C、∵1.5和2.5不是正整数,
∴1.5、2、2.5不是一组勾股数,故本选项不符合题意;
D、∵3,4,7不能构成三角形,故本选项不符合题意;
故选:A.
2.解:A、32+42=52,符合勾股定理的逆定理,故本选项不符合题意;
B、22+32≠42,不符合勾股定理的逆定理,故本选项符合题意;
C、72+242=252,符合勾股定理的逆定理,故本选项不符合题意;
D、92+122=152,符合勾股定理的逆定理,故本选项不符合题意.
故选:B.
3.解:由图可知:
∴AB2+BC2=AC2,AB=BC,
∴△ABC为等腰直角三角形,∠ABC=90°,
∴∠ACB=45°.
故选:B.
4.解:A、∵c2=a2+b2,
∴能判定△ABC为直角三角形,
故A不符合题意;
B、∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴能判定△ABC为直角三角形,
故B不符合题意;
C、∵∠A:∠B:∠C=2:3:5,∠A+∠B+∠C=180°,
∴∠C=180°×=90°,
∴能判定△ABC为直角三角形,
故C不符合题意;
D、∵a=6,b=12,c=13,
∴a2+b2=62+122=180,c2=132=169,
∴a2+b2≠c2,
∴不能判定△ABC为直角三角形,
故D符合题意;
故选:D.
5.解:∵82+152=172,92+122=152,
∴用长度为8,15,17和9,12,15的小木棒能分别摆成两个直角三角形,
故选:C.
6.解:∵BC2﹣AC2=AB2,
∴BC2=AC2+AB2,
∴△ABC是直角三角形,
∴∠A=90°,
∵∠B=25°,
∴∠C=90°﹣∠B=65°,
故选:C.
7.解:如图,分情况讨论:
①AB为直角△ABC斜边时,符合条件的格点C点有2个;
②AB为直角△ABC其中的一条直角边时,符合条件的格点C点有1个.
故共有3个点,
故选:C.
二.填空题
8.解:由题可得,36+64=100,
∴62+82=102,
∴△ABC是直角三角形,且∠ABC=90°,
又∵AB=6,BC=8,
∴△ABC的面积=AB×BC==24.
故答案为:24.
9.解:如图,连接AC,
在△ABC中,AB⊥BC,AB=4,BC=3,
∴AC=5.
在△ADC中,AD=12,CD=13,AC=5.
∵122+52=132,即AD2+AC2=CD2,
∴△ADC是直角三角形,且∠DAC=90°,
∴S四边形ABCD=S△ABC+S△ADC
=AB BC+AC AD
=×4×3+×5×12
=6+30
=36.
故答案为:36.
10.解:∵m为正整数,
∴2m为偶数,设其股是a,则弦为a+2,
根据勾股定理得,(2m)2+a2=(a+2)2,
解得a=m2﹣1,
∴弦是a+2=m2﹣1+2=m2+1,
故答案为:m2+1.
11.解:∵CE平分∠ACB,CF平分∠ACD,
∴∠ACE=∠ACB,∠ACF=∠ACD,即∠ECF=(∠ACB+∠ACD)=90°,
又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,
∴CM=EM=MF=5,EF=10,
由勾股定理可知CE2+CF2=EF2=100.
12.解:如图:延长BA到点D,连接CD,
由题意得:
AD2=22+12=5,
CD2=22+12=5,
AC2=12+32=10,
∴AD2+CD2=AC2,
∴△ACD是直角三角形,
∴∠ADC=90°,
∵AD=CD,
∴∠DAC=∠DCA=45°,
∵∠DAC是△ABC的一个外角,
∴∠DAC=∠ABC+∠ACB=45°,
故答案为:45°.
13.解:∵AD为△ABC的中线,BC=10,
∴BD=CD=BC=5,
∵AB=13,AD=12,
∴52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵CD=BD,
∴AC=AB=13.
故答案为:13.
14.解:如图:连接AE,BE,设AE与BD交于点F,
由题意得:
AB2=12+32=10,
AE2=12+22=5,
EB2=12+22=5,
∴AE=EB,BE2+AE2=AB2,
∴△ABE是等腰直角三角形,
∴∠BAE=45°,
∵BD∥EC,
∴∠ADB=∠ACE,∠AFD=∠AEC,
∵AE=AC,
∴∠AEC=∠ACE,
∴∠AFD=∠ADF,
∵∠AFD是△ABF的一个外角,
∴∠AFD﹣∠ABD=∠BAE=45°,
∴∠ADB﹣∠ABD=45°,
故答案为:45°.
15.解:延长AD到点E,使DE=AD=6,连接CE,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△CED中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=5,∠BAD=∠E,
∵AE=2AD=12,CE=5,AC=13,
∴CE2+AE2=AC2,
∴∠E=90°,
∴∠BAD=90°,
即△ABD为直角三角形,
∴△ABD的面积=AD AB=15,
故答案为:15.
三.解答题
16.(1)证明:连接BD,
∵AB边上的垂直平分线为DE,
∴AD=BD,
∵CB2=AD2﹣CD2,
∴CB2=BD2﹣CD2,
∴CB2+CD2=BD2,
∴∠C=90°;
(2)解:设CD=x,则AD=BD=4﹣x,
在Rt△BCD中,BD2﹣CD2=BC2,
∴(4﹣x)2﹣x2=32,
解得:x=,
∴CD的长为.
17.解:(1)∵AC⊥BC,
∴∠ACB=90°,
∵AB=5,BC=3,
∴AC=4,
∴AC的长为4;
(2)∵AC=4,AD=4,CD2=32,
∴AC2+AD2=42+42=32,CD2=32,
∴AC2+AD2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∵AC=AD=4,
∴∠ACD=∠D=45°,
∵∠ACB=90°,
∴∠BCD=∠ACB+∠ACD=135°,
∴∠BCD的度数为135°;
(3)由题意得:
四边形ABCD的面积=△ABC的面积+△ACD的面积
=AC CB+AD AC
=×4×3+×4×4
=6+8
=14,
∴四边形ABCD的面积为14.
18.证明:连接CE,
∵DE是BC的垂直平分线,
∴EC=BE=5,
在△AEC中,AE=3,EC=5,AC=4,
∵AC2+AE2=42+32=25,EC2=52=25,
∴AC2+AE2=EC2,
∴△AEC是直角三角形,
∴∠A=90°,
∴△ABC是直角三角形.
19.解:(1)△ABC不是直角三角形,△ACD是直角三角形,
理由:∵AD2=52+12=26,AC2+CD2=32+22+32+22=26,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴△ACD是直角三角形,
∵AC2+BC2=13+12+22=18,AB2=42=16,
∴AC2+BC2≠AB2,
∴△ABC不是直角三角形;
(2)D,C,B三点不在一条直线上,
理由:∵∠ACD=90°,∠ACB≠90°,
∴∠BCD≠180°,
∴D,C,B三点不在一条直线上;
(3)由(1)知,∠ACD=90°,
∵AC2=CD2=13,
∴△ACD是等腰直角三角形,
∴∠ADC=45°
20.(1)证明:∵D是边BC的中点,E是边AC的中点,CD=8,CE=6,
∴AC=2CE=12,BC=2CD=16,
∵AB=20,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,
∴∠C=90°;
(2)解:∵E是边AC的中点,AE=6,
∴AC=2AE=12.
在Rt△ACD中,∵∠C=90°,AC=12,AD=13,
∴CD=5,
∴BC=2CD=10,
∴△ABC的面积=AC BC=×12×10=60.
21.解:(1)观察得,a=m2+n2,b=2mn,c=m2﹣n2.
故答案为:m2+n2,2mn,m2﹣n2;
(2)以a,b,c为边长的三角形一定为直角三角形,理由如下:
∵a2=(m2+n2)2=m4+2m2n2+n4,
b2+c2=m4﹣2m2n2+n4+4m2n2=m4+2m2n2+n4,
∴a2=b2+c2,
∴以a,b,c为边长的三角形一定为直角三角形.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
