人教版九年级上册第23章 旋转复习与测试 (含答案)
文档属性
| 名称 | 人教版九年级上册第23章 旋转复习与测试 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 699.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
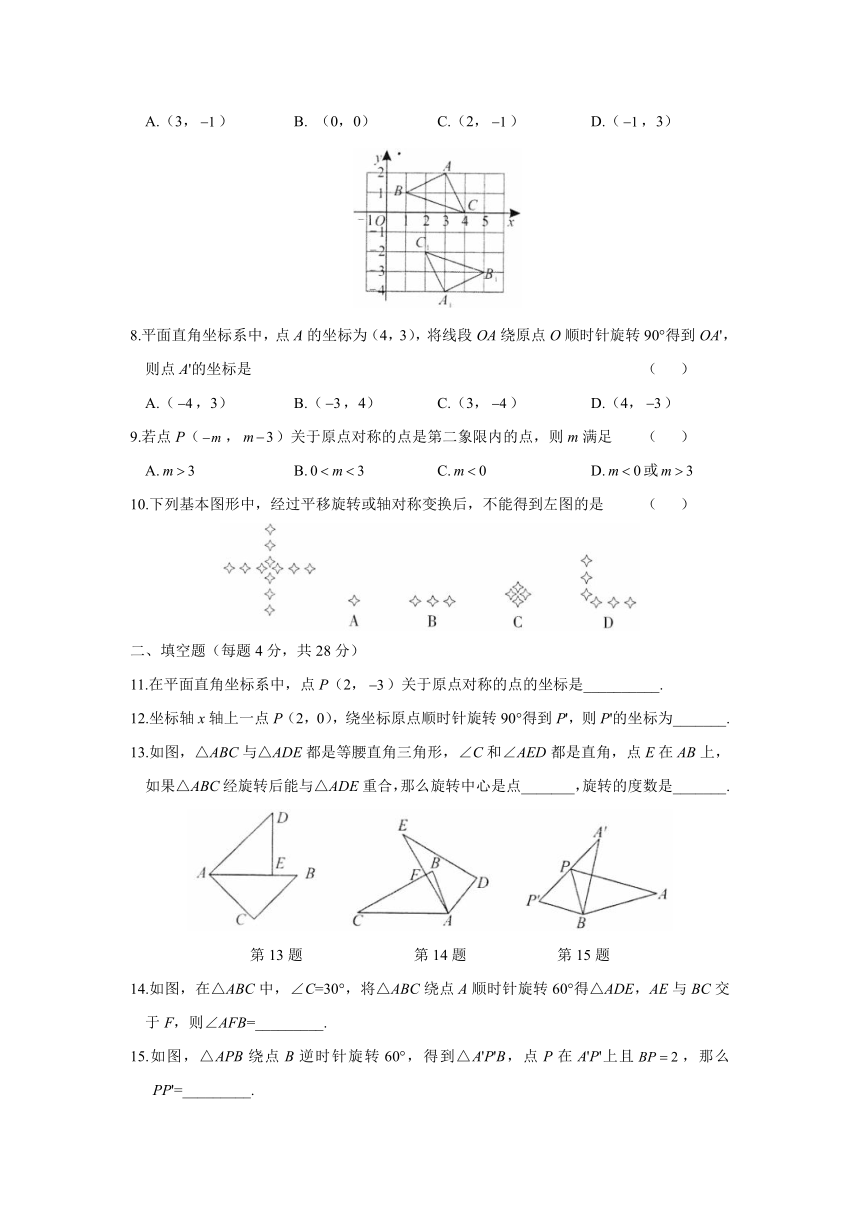
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 06:47:19 | ||
图片预览



文档简介
第23章复习与测试
一、选择题(每题3分,共30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是 ( )
A B C D
2.下列物体的运动:①钟摆的摆动;②风车的旋转;③电梯上下迎送顾客;④关门(不是推拉门),属于旋转的有 ( )
A.1种 B.2种 C.3种 D.4种
3.等边三角形旋转一定角度后能与自身重合,则旋转的角度可能 ( )
A.30° B.60° C.120° D.90°
4.如图,△ABC与△DEF关于点O成中心对称,则下列结论不成立的是 ( )
A.点A与点D是对称点 B.
C.AB//DE D.∠BAC=∠DFE
第4题 第5题
5.如图,点P是等腰直角△ABC内一点,BC是斜边,若将△APB绕点A逆时针旋转到△ADC的位置,则∠APD的度数是 ( )
A.30° B.45° C.50° D.55°
6.图形旋转中,下列说法错误的是 ( )
A.图形上的每一点到旋转中心的距离相等
B.图形上每一点旋转的角度相同
C.图形上可能存在不动的点
D.图形上任意两点的连线与其对应两点的连线长度相等
7.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是 ( )
A.(3,) B. (0,0) C.(2,) D.(,3)
8.平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转90°得到OA',则点A'的坐标是 ( )
A.(,3) B.(,4) C.(3,) D.(4,)
9.若点P(,)关于原点对称的点是第二象限内的点,则m满足 ( )
A. B. C. D.或
10.下列基本图形中,经过平移旋转或轴对称变换后,不能得到左图的是 ( )
二、填空题(每题4分,共28分)
11.在平面直角坐标系中,点P(2,)关于原点对称的点的坐标是__________.
12.坐标轴x轴上一点P(2,0),绕坐标原点顺时针旋转90°得到P',则P'的坐标为_______.
13.如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_______,旋转的度数是_______.
第13题 第14题 第15题
14.如图,在△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于F,则∠AFB=_________.
15.如图,△APB绕点B逆时针旋转60°,得到△A'P'B,点P在A'P'上且,那么PP'=_________.
16.如图,在四边形ABCD中,AD//BC,AB⊥BC,AD=2,BC=3,将边CD以点D为旋转中心逆时针旋转90°至ED,连接AE,则△ADE的面积是_________.
第16题 第17题
17.如图,在△ABO中,AB⊥OB,,,把△ABO绕点O旋转120°后,得到△A1B1O,则点A1的坐标为__________.
三、解答题(一)(每题6分,共18分)
18.在平面直角坐标系中,
(1)画出△ABC关于原点对称的△A1B1C1;
(2)画出△ABC绕原点O顺时针方向旋转90°得到的△A2B2C2.
19.如图,把一个直角三角尺ACB绕着30角的顶点顺时针旋转,使得A与CB的延长线上的E点重合,其中点C的对应点为D点.
(1)三角尺旋转了_________度;
(2)△CBD是_________三角形;
(3)∠BDC的度数为__________度.
20.如图,在等边△ABC中;,点D是BC的中点,将△ABD绕点A旋转后得到△ACE,求线段DE的长度.
四、解答题(二)(每题8分,共24分)
21.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA'.
(1)若∠1=25°,则∠BAA'=_________°;
(2)若,,求△AA'B'的面积与周长.
22.如图,已知△ABC中,,把△ABC绕A点沿顺时针旋转得到△ADE,连接BD,CE,交于点F.
(1)求证:△AEC≌△ADB;
(2)岩,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
23.如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.求证:
(1)EA是∠QED的平分线;
(2).
五、解答题(三)(每题10分,共20分)
24.如图,把一副三角板按如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D'CE',如图②,这时,AB与CD'相交于点O,D'E'与AB相交于点F.
(1)求∠OFE'的度数;
(2)求线段AD'的长.
25.如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图①),求证:M为AN的中点;
(2)将图①的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图②),求证:△CAN为等腰直角三角形;
(3)将图①中△BCE绕点B旋转到图③的位置时,(2)中的结论是否仍然,成立 若成立,试证明;若不成立,请说明理由.
单元测试(3)——旋转
一、1.A 2.C 3.C 4.D 5.B 6.A 7.A 8.C 9.C 10.C
二、11.(,3) 12.(0,) 13.A 45° 14.90° 15.2
16. 1 17.(,0)或(1,)
三、18.解:(1)如图所示,△A1B1C1即为所求作;
(1)如图所示,△A2B2C2即为所求作.
19.解:(1)△ABC旋转后AB与BE重合,∠ABC=30°,
∴,
∴三角尺旋转了150°.
(2)∵△EBD由△ABC旋转而成,
∴△ABC≌△EBD,
∴,
∴△CBD是等腰三角形.
(3)∵△ABC≌△EBD,
∴∠EBD=∠ABC=30°,
∴°.
∵△CBD是等腰三角形,
∴
故答案为150;等腰;15.
20.解:△ABC是等边三角形,
∴,∠BAC=60°,
∵点D是BC的中点,
∴,AD⊥BC,
∴
由旋转可知∠DAE=∠BAC=60°,,
∴△ADE是等边三角形,
∴.
四、21.解:(1)∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A'B'C,
∴AC=A'C,∠CA'B'=∠BAC,
∴△ACA'是等腰直角三角形,
∴∠CA'A=45°,
∴,
∴,
∴
(2)由旋转的意义可知△ABC≌△A'B'C,
∴B'C=BC=1,A'C=AC=3,∠A'CB'=90°
∴
∴
在Rt△A'CB'中,
在Rt△ACA'中,
∴
22.(1)证明:由旋转的性质,得
△ABC≌△ADE,且,
∴,∠BAC=∠DAE,AD=DF=FC=AC=AB=2,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠BAD,
在△AEC和△ADB中,
△AEC≌△ADB(SAS)
(2)解:∵四边形ADFC是菱形,且∠BAC=45°,
∴∠DBA=∠BAC=45°,
由(1)得:,
∴∠DBA=∠BDA=45°,
∴△ABD为直角边为2的等腰直角三角形,
∴,即,
∴.
23.证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠FAQ=90°,
∵∠EAF =45°,∠QAE =45°,
∴∠QAE=∠FAE,
在△AQE和△AFE中,
∴△AQE≌△AFE(SAS)
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线;
(2)由(1)知△AQE≌△AFE,
∴QE=EF,
由旋转知,∠QBA=∠FDA=45°
∴∠QBE=∠QBA+∠ABD
=45°+45°=90°
在Rt△QBE中,
,
又∵QB=DF,∴.
24.解:(1)如图,由题意可知∠3=15°,∠E'=90°,
∵∠1=∠2,∴∠1=75°.
又∵∠B=45°,
∴∠OFE'=∠B+∠1=45°+75°=120°.
(2)连接AD'.
∵∠OFE'=120°,
∴∠D'FO=60°.
又∠CD'E'=30°,∴∠4=90°.
∵AC=BC,AB=6cm,
∴OA=OB=3cm,又∠ACB=90°,
∴(cm).
又∵CD'=7cm,
∴OD'=CD'-CO
(cm).
在Rt△AD'O中,
(cm).
25.(1)证明:∵EN//AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为DE的中点,
∴DM=EM.
在△ADM和△NEM中,
∴△ADM≌△NEM.
∴AM=MN.∴M为AN的中点.
(2)证明:∵△BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD//NE,
∴∠DAE+∠NEA=180°.
∵∠DAE=90°,
∴∠NEA=90°.
∴∠NEC=∠CEB+∠NEA
.
∵A,B,E三点在同一直线上,
∴.
∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),
∴AD=NE.
∵AD=AB,∴AB=NE.
在△ABC和△NEC中,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠ACB+∠BCN
=∠NCE+∠BCN
=∠BCE=90°.
∴△ACN为等腰直角三角形.
(3)解:△ACN仍为等腰直角三角形,证明如下:
延长AB,交NE于F.
∵AD//NE,M为中点,
∴易得△ADM≌△NEM,
∴AD=NE.
∵AD=AB,
∴AB=NE.
∵AD//NE,
∴AF⊥NE,
在四边形BCEF中,
∵∠BCE=∠BFE=90°
∴
∵∠FBC+∠ABC=180°
∴∠ABC=∠FEC
在△ABC和△NEC中,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACB+∠NCB=∠NCE+∠NCB
即∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
一、选择题(每题3分,共30分)
1.下列图形中,既是轴对称图形又是中心对称图形的是 ( )
A B C D
2.下列物体的运动:①钟摆的摆动;②风车的旋转;③电梯上下迎送顾客;④关门(不是推拉门),属于旋转的有 ( )
A.1种 B.2种 C.3种 D.4种
3.等边三角形旋转一定角度后能与自身重合,则旋转的角度可能 ( )
A.30° B.60° C.120° D.90°
4.如图,△ABC与△DEF关于点O成中心对称,则下列结论不成立的是 ( )
A.点A与点D是对称点 B.
C.AB//DE D.∠BAC=∠DFE
第4题 第5题
5.如图,点P是等腰直角△ABC内一点,BC是斜边,若将△APB绕点A逆时针旋转到△ADC的位置,则∠APD的度数是 ( )
A.30° B.45° C.50° D.55°
6.图形旋转中,下列说法错误的是 ( )
A.图形上的每一点到旋转中心的距离相等
B.图形上每一点旋转的角度相同
C.图形上可能存在不动的点
D.图形上任意两点的连线与其对应两点的连线长度相等
7.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是 ( )
A.(3,) B. (0,0) C.(2,) D.(,3)
8.平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转90°得到OA',则点A'的坐标是 ( )
A.(,3) B.(,4) C.(3,) D.(4,)
9.若点P(,)关于原点对称的点是第二象限内的点,则m满足 ( )
A. B. C. D.或
10.下列基本图形中,经过平移旋转或轴对称变换后,不能得到左图的是 ( )
二、填空题(每题4分,共28分)
11.在平面直角坐标系中,点P(2,)关于原点对称的点的坐标是__________.
12.坐标轴x轴上一点P(2,0),绕坐标原点顺时针旋转90°得到P',则P'的坐标为_______.
13.如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点_______,旋转的度数是_______.
第13题 第14题 第15题
14.如图,在△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于F,则∠AFB=_________.
15.如图,△APB绕点B逆时针旋转60°,得到△A'P'B,点P在A'P'上且,那么PP'=_________.
16.如图,在四边形ABCD中,AD//BC,AB⊥BC,AD=2,BC=3,将边CD以点D为旋转中心逆时针旋转90°至ED,连接AE,则△ADE的面积是_________.
第16题 第17题
17.如图,在△ABO中,AB⊥OB,,,把△ABO绕点O旋转120°后,得到△A1B1O,则点A1的坐标为__________.
三、解答题(一)(每题6分,共18分)
18.在平面直角坐标系中,
(1)画出△ABC关于原点对称的△A1B1C1;
(2)画出△ABC绕原点O顺时针方向旋转90°得到的△A2B2C2.
19.如图,把一个直角三角尺ACB绕着30角的顶点顺时针旋转,使得A与CB的延长线上的E点重合,其中点C的对应点为D点.
(1)三角尺旋转了_________度;
(2)△CBD是_________三角形;
(3)∠BDC的度数为__________度.
20.如图,在等边△ABC中;,点D是BC的中点,将△ABD绕点A旋转后得到△ACE,求线段DE的长度.
四、解答题(二)(每题8分,共24分)
21.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA'.
(1)若∠1=25°,则∠BAA'=_________°;
(2)若,,求△AA'B'的面积与周长.
22.如图,已知△ABC中,,把△ABC绕A点沿顺时针旋转得到△ADE,连接BD,CE,交于点F.
(1)求证:△AEC≌△ADB;
(2)岩,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
23.如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.求证:
(1)EA是∠QED的平分线;
(2).
五、解答题(三)(每题10分,共20分)
24.如图,把一副三角板按如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D'CE',如图②,这时,AB与CD'相交于点O,D'E'与AB相交于点F.
(1)求∠OFE'的度数;
(2)求线段AD'的长.
25.如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图①),求证:M为AN的中点;
(2)将图①的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图②),求证:△CAN为等腰直角三角形;
(3)将图①中△BCE绕点B旋转到图③的位置时,(2)中的结论是否仍然,成立 若成立,试证明;若不成立,请说明理由.
单元测试(3)——旋转
一、1.A 2.C 3.C 4.D 5.B 6.A 7.A 8.C 9.C 10.C
二、11.(,3) 12.(0,) 13.A 45° 14.90° 15.2
16. 1 17.(,0)或(1,)
三、18.解:(1)如图所示,△A1B1C1即为所求作;
(1)如图所示,△A2B2C2即为所求作.
19.解:(1)△ABC旋转后AB与BE重合,∠ABC=30°,
∴,
∴三角尺旋转了150°.
(2)∵△EBD由△ABC旋转而成,
∴△ABC≌△EBD,
∴,
∴△CBD是等腰三角形.
(3)∵△ABC≌△EBD,
∴∠EBD=∠ABC=30°,
∴°.
∵△CBD是等腰三角形,
∴
故答案为150;等腰;15.
20.解:△ABC是等边三角形,
∴,∠BAC=60°,
∵点D是BC的中点,
∴,AD⊥BC,
∴
由旋转可知∠DAE=∠BAC=60°,,
∴△ADE是等边三角形,
∴.
四、21.解:(1)∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A'B'C,
∴AC=A'C,∠CA'B'=∠BAC,
∴△ACA'是等腰直角三角形,
∴∠CA'A=45°,
∴,
∴,
∴
(2)由旋转的意义可知△ABC≌△A'B'C,
∴B'C=BC=1,A'C=AC=3,∠A'CB'=90°
∴
∴
在Rt△A'CB'中,
在Rt△ACA'中,
∴
22.(1)证明:由旋转的性质,得
△ABC≌△ADE,且,
∴,∠BAC=∠DAE,AD=DF=FC=AC=AB=2,
∴∠BAC+∠BAE=∠DAE+∠BAE,
即∠CAE=∠BAD,
在△AEC和△ADB中,
△AEC≌△ADB(SAS)
(2)解:∵四边形ADFC是菱形,且∠BAC=45°,
∴∠DBA=∠BAC=45°,
由(1)得:,
∴∠DBA=∠BDA=45°,
∴△ABD为直角边为2的等腰直角三角形,
∴,即,
∴.
23.证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠FAQ=90°,
∵∠EAF =45°,∠QAE =45°,
∴∠QAE=∠FAE,
在△AQE和△AFE中,
∴△AQE≌△AFE(SAS)
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线;
(2)由(1)知△AQE≌△AFE,
∴QE=EF,
由旋转知,∠QBA=∠FDA=45°
∴∠QBE=∠QBA+∠ABD
=45°+45°=90°
在Rt△QBE中,
,
又∵QB=DF,∴.
24.解:(1)如图,由题意可知∠3=15°,∠E'=90°,
∵∠1=∠2,∴∠1=75°.
又∵∠B=45°,
∴∠OFE'=∠B+∠1=45°+75°=120°.
(2)连接AD'.
∵∠OFE'=120°,
∴∠D'FO=60°.
又∠CD'E'=30°,∴∠4=90°.
∵AC=BC,AB=6cm,
∴OA=OB=3cm,又∠ACB=90°,
∴(cm).
又∵CD'=7cm,
∴OD'=CD'-CO
(cm).
在Rt△AD'O中,
(cm).
25.(1)证明:∵EN//AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为DE的中点,
∴DM=EM.
在△ADM和△NEM中,
∴△ADM≌△NEM.
∴AM=MN.∴M为AN的中点.
(2)证明:∵△BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD//NE,
∴∠DAE+∠NEA=180°.
∵∠DAE=90°,
∴∠NEA=90°.
∴∠NEC=∠CEB+∠NEA
.
∵A,B,E三点在同一直线上,
∴.
∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),
∴AD=NE.
∵AD=AB,∴AB=NE.
在△ABC和△NEC中,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠ACB+∠BCN
=∠NCE+∠BCN
=∠BCE=90°.
∴△ACN为等腰直角三角形.
(3)解:△ACN仍为等腰直角三角形,证明如下:
延长AB,交NE于F.
∵AD//NE,M为中点,
∴易得△ADM≌△NEM,
∴AD=NE.
∵AD=AB,
∴AB=NE.
∵AD//NE,
∴AF⊥NE,
在四边形BCEF中,
∵∠BCE=∠BFE=90°
∴
∵∠FBC+∠ABC=180°
∴∠ABC=∠FEC
在△ABC和△NEC中,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACB+∠NCB=∠NCE+∠NCB
即∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
同课章节目录
