第6章 平面图形的认识(一) 复习与测试(含解析)
文档属性
| 名称 | 第6章 平面图形的认识(一) 复习与测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 607.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 09:26:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第6章复习与测试
一、选择题
1、已知OC平分∠AOB,∠AOB=64°,则∠AOC的度数是( )
A.64° B.32° C.128° D.不能计算
2、已知∠a=25,则∠a的补角的度数是( )
A.65° B.75° C.155° D.165°
3、如果∠α=52°25′,则∠α的余角的度数为( )
A.38°25′ B.37°45′ C.37°35′ D.127°35′
4、15点整时针与分针的夹角度数为( )
A.60° B.75° C.90° D.100°
5、将一副三角板按如图所示的方式放置,则∠AOB=( )
A.30° B.45° C.75° D.80°
(5题) (6题) (7题)
6、如图,直线AB、CD相交于点O,OE平分∠AOD,若∠1=38°,则∠COE等于( )
A.66° B.76° C.109° D.144°
7、如图,甲从处出发沿北偏东方向走到处,乙从处出发沿南偏西 方向走到处,则的度数是( )
A. B. C. D.
8、如图,将一副三角板的直角顶点重合摆放在桌面上,下列各组角中一定能互补的是( )
A.∠BCE和∠ACE B.∠ACD和∠ACE
C.∠DCB和∠ACE D.∠DCB和∠ACB
(8题) (9题) (10题)
9、如图,∠AOB=90°,∠BOC=15°,OC平分∠AOD,则∠BOD的度数是( )
A.75° B.60° C.65° D.55°
10、如图,已知是直角,OM平分,ON平分,则的度数是( )
A.30° B.45° C.50° D.60°
二、填空题
11、如图,两直线交于点O,若∠1+∠2=76°,则∠1= 度.
12、如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
13、如图,直线,相交于点O,,,则的度数为__________.
(13题) (14题) (15题)
14、如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠BOD等于_____.
15、如图所示,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11,则∠AOB=_______.
16、如图,AB、CD相交于点O,OB平分.若,则的度数是________.
(16题) (17题) (18题)
17、如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的平分线,则∠BAD的度数为___°.
18、如图,直线AB,CD相交于点O,OF平分∠BOD,OE平分∠COF,∠AOD:∠BOF=4:1,
则∠AOE= .
三、解答题
19、如图:∠AOB=160°,OC是∠AOB的平分线,OD是∠COB的平分线,求∠COD的度数.
20、如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC.求∠BOD的度数.
21、如图,直线相交于点平分,求:
(1)的度数.
(2)的度数.
22、如图,已知直线AE, O 是直线AE上一点.OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=30°
(1)求∠AOC的度数;
(2)求∠COE的度数;
(3)求∠BOD的度数.
23、如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=65°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
24、如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
(1)图中∠AOD的补角是 ;∠BOD的余角是 .
(2)已知∠COD=40°,求∠COE的度数.
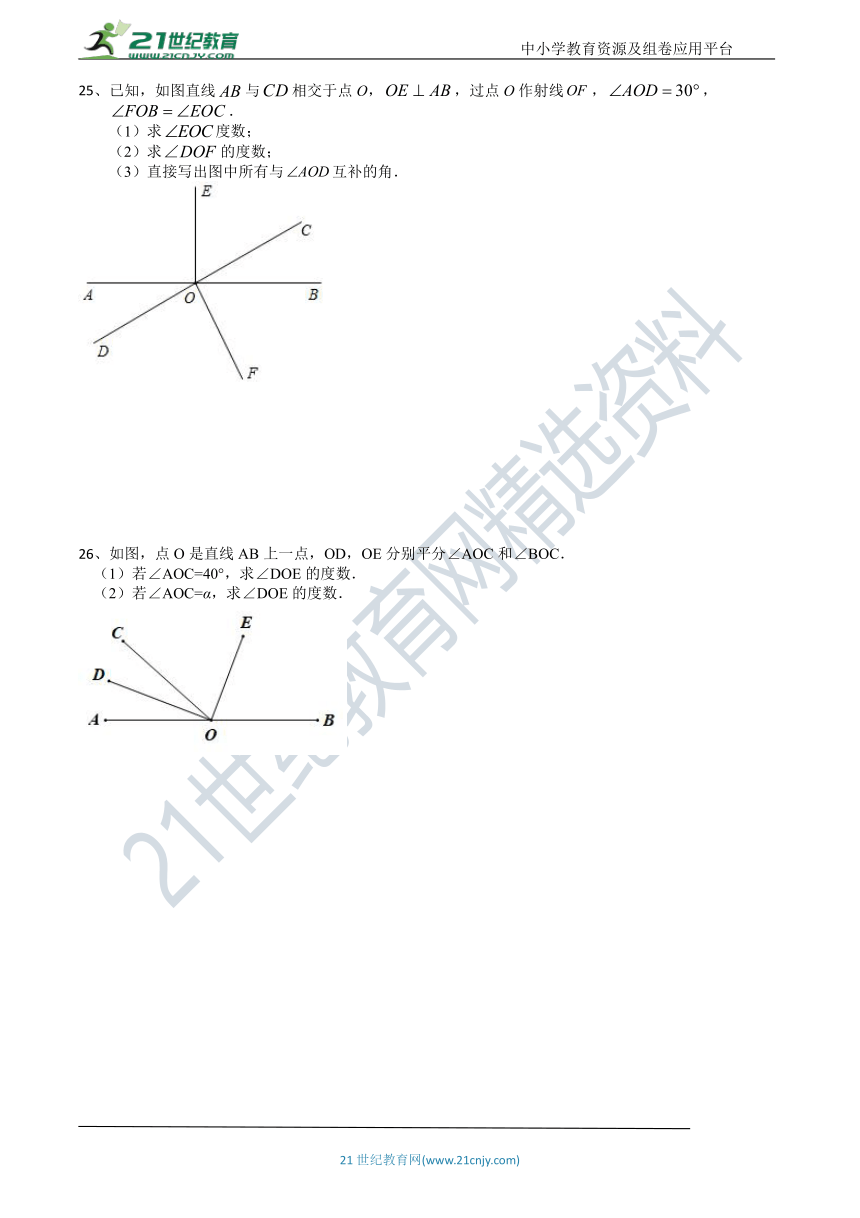
25、已知,如图直线与相交于点O,,过点O作射线,,.
(1)求度数;
(2)求的度数;
(3)直接写出图中所有与互补的角.
26、如图,点O是直线AB上一点,OD,OE分别平分∠AOC和∠BOC.
(1)若∠AOC=40°,求∠DOE的度数.
(2)若∠AOC=α,求∠DOE的度数.
2021-2022学年苏科版七年级数学上册 寒假专题训练(角的计算)(解析)
一、选择题
1、已知OC平分∠AOB,∠AOB=64°,则∠AOC的度数是( )
A.64° B.32° C.128° D.不能计算
【答案】B
【分析】
直接根据角平分线的定义得出∠AOC=∠AOB,再计算即可.
【详解】
解:∵∠AOB=64°,OC平分∠AOB,
∴∠AOC=∠AOB=×64°=32°.
故选:B.
2、已知∠a=25,则∠a的补角的度数是( )
A.65° B.75° C.155° D.165°
【答案】C
【分析】
根据补角的定义得出∠A的补角是180°-∠a,代入求出即可.
【详解】
解:∵∠a =25°,
∴∠a的补角是180°-∠a =180°-25°=155°.
故选:C.
3、如果∠α=52°25′,则∠α的余角的度数为( )
A.38°25′ B.37°45′ C.37°35′ D.127°35′
【答案】C
【分析】
根据互余的两个角的和等于90°列式计算即可得解.
【详解】
解:∵∠α=52°25′,
则∠α的余角的度数=90°﹣52°25′=89°60'﹣52°25'=37°35′.
故选:C.
4、15点整时针与分针的夹角度数为( )
A.60° B.75° C.90° D.100°
【答案】C
【分析】
钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,15点整时,时针指到3上,分针指到12上,15点整时针和分针夹角是3份即可得出答案.
【详解】
解:15点整,时针和分针夹角是3份,每份30°,
故3×30°=90°.
故选:C.
5、将一副三角板按如图所示的方式放置,则∠AOB=( )
A.30° B.45° C.75° D.80°
【答案】C
【分析】
根据一幅直角三角板的度数有60°,45°,30°,90°,即可得到答案.
【详解】
根据题意,得:∠AOB=45°+30°=75°.
故选C.
6、如图,直线AB、CD相交于点O,OE平分∠AOD,若∠1=38°,则∠COE等于( )
A.66° B.76° C.109° D.144°
【答案】C
【分析】
根据邻补角的概念求出∠AOD,根据角平分线的定义求出∠DOE,再根据邻补角的概念计算,得到答案.
【详解】
解:∵∠1=38°,
∴∠AOD=180°﹣∠1=142°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=71°,
∴∠COE=180°﹣∠DOE=109°,
故选:C.
7、如图,甲从处出发沿北偏东方向走到处,乙从处出发沿南偏西 方向走到处,则的度数是( )
A. B. C. D.
【答案】C
【分析】
根据题意得到∠EAD=∠DOF=90°,先求出∠BAD=30°,再根据∠BAC=∠EAD+∠DAF+∠CAF即可求解.
【详解】
解:如图,由题意得∠EAD=∠DOF=90°,
∵∠EAB=60°,
∴∠BAD=∠EAD-∠EAB=90°-60°=30°,
∴∠BAC=∠BAD+∠DAF+∠CAF=30°+90°+30°=120°.
故选:C
8、如图,将一副三角板的直角顶点重合摆放在桌面上,下列各组角中一定能互补的是( )
A.∠BCE和∠ACE B.∠ACD和∠ACE
C.∠DCB和∠ACE D.∠DCB和∠ACB
【答案】C
【分析】
分别将四个选项中的两个角相加,如果和为,那么这两个角互补.
【详解】
A选项、∵,
∴和不一定互补,故不符合题意;
B选项、∵,
∴和不一定互补,故不符合题意;
C选项、∵,
∴和互补,符合题意;
D选项、∵,
∴和不一定互补,故不符合题意;
故选:C.
9、如图,∠AOB=90°,∠BOC=15°,OC平分∠AOD,则∠BOD的度数是( )
A.75° B.60° C.65° D.55°
【答案】B
【分析】
先求出∠AOC,再根据角平分线的定义求出∠AOD,然后根据∠BOD=∠AOD﹣∠AOB代入数据进行计算即可得解.
【详解】
解:∵∠AOB=90°,∠BOC=15°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣15°=75°,
∵OC平分∠AOD,
∴∠AOD=2∠AOC=2×75°=150°,
∴∠BOD=∠AOD﹣∠AOB=150°﹣90°=60°,
故选:B.
10、如图,已知是直角,OM平分,ON平分,则的度数是( )
A.30° B.45° C.50° D.60°
【答案】B
【分析】
由角平分线的定义可得,∠COM=∠AOC,∠NOC=∠BOC,再根据∠MON=∠MOC-∠NOC解答即可.
【详解】
∵OM平分,∴∠COM=∠AOC,
∵ON平分∠BOC,∴∠NOC=∠BOC,
∴∠MON=∠MOC-∠NOC= (∠AOC-∠BOC)=∠AOB=45°.
故选B.
二、填空题
11、如图,两直线交于点O,若∠1+∠2=76°,则∠1= 度.
【分析】直接利用对顶角的性质结合已知得出答案.
【解析】∵两直线交于点O,
∴∠1=∠2,
∵∠1+∠2=76°,
∴∠1=38°.
故答案为:38.
12、如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
【分析】根据对顶角相等可得∠1的度数,再利用邻补角互补可得答案.
【解析】∵∠1=∠2,∠1+∠2=220°,
∴∠1=∠2=110°,
∴∠3=180°﹣110°=70°,
故答案为:70°.
13、如图,直线,相交于点O,,,则的度数为__________.
【答案】110
【分析】
先根据对顶角相等求出∠DOB,进而结合即可求出∠EOB.
【详解】
解:∵∠1=35°,
∴∠DOB=∠1=35°,
又∵∠2=75°,
∴∠EOB=∠2+∠DOB=110°.
故答案为:110.
14、如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠BOD等于_____.
【答案】75°
【分析】
依据OD是∠AOC的平分线,即可得到∠AOC=2∠COD=50°,再根据OC是∠AOB的平分线,即可得到∠BOC=∠AOC=50°,进而得出∠BOD=75°.
【详解】
解:∵OD是∠AOC的平分线,且∠COD=25°,
∴∠AOC=2∠COD=50°,
又∵OC是∠AOB的平分线,
∴∠BOC=∠AOC=50°,
∴∠BOD=∠BOC+∠COD=50°+25°=75°,
故答案为:75°.
15、如图所示,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11,则∠AOB=_______.
【答案】20°
【分析】
由∠AOB+∠BOC=∠BOC+∠COD知∠AOB=∠COD,设∠AOB=2α,则∠AOD=11α,故∠AOB+∠BOC=5α=90°,解得α即可.
【详解】
解:∵∠AOB+∠BOC=∠BOC+∠COD,
∴∠AOB=∠COD,
设∠AOB=2α,
∵∠AOB:∠AOD=2:11,
∴∠AOB+∠BOC=9α=90°,
解得α=10°,
∴∠AOB=20°.
故答案为20°.
16、如图,AB、CD相交于点O,OB平分.若,则的度数是________.
【答案】
【分析】
根据对顶角相等可得出∠BOD的度数,根据角平分线的性质可得出∠DOE.
【详解】
解:∵∠AOC和∠BOD是对顶角,
∴∠BOD=∠AOC=30°,
∵OB平分∠DOE,
∴∠DOE=2∠BOD=60°.
故答案为:60°.
17、如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的平分线,则∠BAD的度数为___°.
【答案】80
【分析】
由∠BAE=110°,∠CAE=60°,可得∠BAC=110°﹣60°=50°,结合∠CAF=110°,可得∠BAF=110°+50°=160°,再由AD平分∠BAF即可得∠BAD=80°.
【详解】
∵∠BAE=110°,∠CAE=60°,
∴∠BAC=110°﹣60°=50°,
又∵∠CAF=110°,
∴∠BAF=110°+50°=160°,
又∵AD是∠BAF的角平分线,
∴∠BAD=∠BAF=×160°=80°.
故答案为:80.
18、如图,直线AB,CD相交于点O,OF平分∠BOD,OE平分∠COF,∠AOD:∠BOF=4:1,
则∠AOE= .
【分析】根据角平分线的定义得出∠BOD=2∠BOF,∠BOF=∠DOF,根据∠AOD:∠BOF=4:1求出∠AOD:∠BOD=4:2,根据邻补角互补求出∠AOD=120°,∠BOD=60°,求出∠AOC=60°,根据角平分线定义求出∠COE,再求出答案即可.
【解析】∵OF平分∠BOD,∴∠BOD=2∠BOF,∠BOF=∠DOF,
∵∠AOD:∠BOF=4:1,∴∠AOD:∠BOD=4:2,
∵∠AOD+∠BOD=180°,
∴∠AOD=120°,∠BOD=60°,∴∠AOC=∠BOD=60°,
∴∠BOF=∠DOF==30°,∴∠COF=180°﹣∠DOF=150°,
∵OE平分∠COF,∴∠COE=COF=,
∴∠AOE=∠AOC+∠COE=60°+75°=135°,
故答案为:135°.
三、解答题
19、如图:∠AOB=160°,OC是∠AOB的平分线,OD是∠COB的平分线,求∠COD的度数.
【答案】40°
【分析】
根据角平分线的定义得出∠COB=∠AOB,∠COD=∠COB,即可求出答案.
【详解】
解:∵OC是∠AOB的平分线,∠AOB=160°,
∴∠COB=∠AOB =×160°=80°,
又∵OD是∠COB的平分线,
∴∠COD=∠COB =×80°=40°.
20、如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC.求∠BOD的度数.
【分析】直接利用角平分线的定义结合对顶角的性质得出答案.
【解析】∵∠EOC=70°,OA平分∠EOC,
∴∠EOA=∠AOC=70°=35°,
∴∠BOD=∠AOC=35°.
21、如图,直线相交于点平分,求:
(1)的度数.
(2)的度数.
【答案】(1)140°;(2)40°
【分析】
(1)根据平角的定义可得,利用角平分线的定义可得,再根据平角的定义即可求解;
(2)直接利用对顶角相等即可求解.
【详解】
解:(1)∵∠,
∴,
∵OB平分,
∴,
∴;
(2)∵,
∴.
22、如图,已知直线AE, O 是直线AE上一点.OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=30°
(1)求∠AOC的度数;
(2)求∠COE的度数;
(3)求∠BOD的度数.
【答案】(1)60°;(2)120°;(3)90°
【分析】
(1)根据角平分线的定义求解即可;
(2)根据平角定义即可求解;
(3)根据角平分线的定义求得∠COD,进而可求得∠BOD的度数.
【详解】
解:(1)∵OB是∠AOC的平分线,∠AOB=30°,
∴∠BOC=∠AOB=30°,
∴∠AOC=2∠AOB=60°;
(2)∵∠AOC+∠COE=180°,
∴∠COE=180°﹣∠AOC=180°﹣60°=120°;
(3)∵OD是∠COE的平分线,
∴∠COD= ∠COE=60°,
∴∠BOD=∠COD+∠BOC=60°+30°=90°.
23、如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=65°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
【答案】(1)115°;(2)45°
【分析】
(1)根据角平分线的定义,得出∠EOC=∠BOE=65°,利用邻补角定义求出∠DOE即可;
(2)根据角平分线的定义,∠BOD:∠BOE=2:3,求出∠BOD,再根据对顶角可求出∠AOC,利用垂直,求出∠AOF.
【详解】
(1)∵OE平分∠BOC,∠BOE=65°,
∴∠EOC=∠BOE=65°,
∴∠DOE=180°-∠EOC=180°-65°=115°;
(2)∵OE平分∠BOC,
∴∠EOC=∠BOE,
∵∠BOD:∠BOE=2:3,
设∠BOD=x,则∠COE=∠BOE=,
∵∠COE+∠BOE+∠BOD=180°,
∴,
∴x=45°,
∵OF⊥CD,∠BOD=∠AOC,
∴∠BOD=∠AOC=45°,
∴∠COF=90°,
∴∠AOF=∠COF-∠AOC=90°-45°=45°.
24、如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
(1)图中∠AOD的补角是 ;∠BOD的余角是 .
(2)已知∠COD=40°,求∠COE的度数.
【答案】(1)∠BOD,∠COD;∠COE,∠AOE;(2)50°
【分析】
(1)根据“和为180°的两个角互为补角”、“和为90°的两个角互为余角”进行解答;
(2)∠AOB是平角,∠AOB=∠AOC+∠BOC以及角平分线的定义进行求解即可.
【详解】
(1)∵∠AOD+∠BOD=180°
∴∠BOD是∠AOD的补角;
∵OD平分∠BOC,OE平分∠AOC,
∴ ,
∴,
∴∠AOE和∠EOC是∠BOD的余角;∠COD和∠BOD是∠AOD的补角;
故答案为:∠BOD,∠COD;∠COE,∠AOE;
(2)解:∵OD平分∠BOC,∠COD=40°
∴∠BOC=2∠COD=80°
由题意可知,∠AOB是平角,∠AOB=∠AOC+∠BOC
∴∠AOC=∠AOB-∠BOC
=180°-80°
=100°
∵OE平分∠AOC,
∴∠COE=∠AOC=50°.
25、已知,如图直线与相交于点O,,过点O作射线,,.
(1)求度数;
(2)求的度数;
(3)直接写出图中所有与互补的角.
【答案】(1)60°(2)90°(3)、、
【分析】
(1)根据垂直的定义得到,由对顶角的性质得到,即可得出结论;
(2)根据平角的定义即可得出结论;
(3)根据补角的定义即可得出结论.
【详解】
解:(1)∵,
∴,
∵,
∴=60°;
(2)∵=60°,
∴;
(3)∵,
,
,
∴与互补的角为:、、.
26、如图,点O是直线AB上一点,OD,OE分别平分∠AOC和∠BOC.
(1)若∠AOC=40°,求∠DOE的度数.
(2)若∠AOC=α,求∠DOE的度数.
【答案】(1)90°;(2)90°.
【分析】
(1)根据∠AOC=40°,则可计算出∠BOC=140°,再根据角平分线的定义得到∠COD=∠AOC=20°,∠COE=∠BOC=70°,然后利用∠DOE=∠COD+∠COE进行计算,即可求∠DOE的度数;
(2)根据∠AOC=α,则可计算出∠BOC=180° α,再根据角平分线的定义得到∠COD=∠AOC=α,∠COE=∠BOC=90° α,然后利用∠DOE=∠COD+∠COE进行计算即可.
【详解】
解:(1)∵∠AOC=40°,
∴∠BOC=180° ∠AOC=140°.
∵OD,OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOC=×40°=20°,
∠COE=∠BOC=×140°=70°.
∴∠DOE=∠COD+∠COE=20°+70°=90°.
(2)∵∠AOC=α,
∴∠BOC=180° ∠AOC=180° α.
∵OD,OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOC=α,
∠COE=∠BOC=(180 α)=90° α.
∴∠DOE=∠COD+∠COE=α+(90° α)=90°.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第6章复习与测试
一、选择题
1、已知OC平分∠AOB,∠AOB=64°,则∠AOC的度数是( )
A.64° B.32° C.128° D.不能计算
2、已知∠a=25,则∠a的补角的度数是( )
A.65° B.75° C.155° D.165°
3、如果∠α=52°25′,则∠α的余角的度数为( )
A.38°25′ B.37°45′ C.37°35′ D.127°35′
4、15点整时针与分针的夹角度数为( )
A.60° B.75° C.90° D.100°
5、将一副三角板按如图所示的方式放置,则∠AOB=( )
A.30° B.45° C.75° D.80°
(5题) (6题) (7题)
6、如图,直线AB、CD相交于点O,OE平分∠AOD,若∠1=38°,则∠COE等于( )
A.66° B.76° C.109° D.144°
7、如图,甲从处出发沿北偏东方向走到处,乙从处出发沿南偏西 方向走到处,则的度数是( )
A. B. C. D.
8、如图,将一副三角板的直角顶点重合摆放在桌面上,下列各组角中一定能互补的是( )
A.∠BCE和∠ACE B.∠ACD和∠ACE
C.∠DCB和∠ACE D.∠DCB和∠ACB
(8题) (9题) (10题)
9、如图,∠AOB=90°,∠BOC=15°,OC平分∠AOD,则∠BOD的度数是( )
A.75° B.60° C.65° D.55°
10、如图,已知是直角,OM平分,ON平分,则的度数是( )
A.30° B.45° C.50° D.60°
二、填空题
11、如图,两直线交于点O,若∠1+∠2=76°,则∠1= 度.
12、如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
13、如图,直线,相交于点O,,,则的度数为__________.
(13题) (14题) (15题)
14、如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠BOD等于_____.
15、如图所示,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11,则∠AOB=_______.
16、如图,AB、CD相交于点O,OB平分.若,则的度数是________.
(16题) (17题) (18题)
17、如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的平分线,则∠BAD的度数为___°.
18、如图,直线AB,CD相交于点O,OF平分∠BOD,OE平分∠COF,∠AOD:∠BOF=4:1,
则∠AOE= .
三、解答题
19、如图:∠AOB=160°,OC是∠AOB的平分线,OD是∠COB的平分线,求∠COD的度数.
20、如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC.求∠BOD的度数.
21、如图,直线相交于点平分,求:
(1)的度数.
(2)的度数.
22、如图,已知直线AE, O 是直线AE上一点.OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=30°
(1)求∠AOC的度数;
(2)求∠COE的度数;
(3)求∠BOD的度数.
23、如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=65°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
24、如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
(1)图中∠AOD的补角是 ;∠BOD的余角是 .
(2)已知∠COD=40°,求∠COE的度数.
25、已知,如图直线与相交于点O,,过点O作射线,,.
(1)求度数;
(2)求的度数;
(3)直接写出图中所有与互补的角.
26、如图,点O是直线AB上一点,OD,OE分别平分∠AOC和∠BOC.
(1)若∠AOC=40°,求∠DOE的度数.
(2)若∠AOC=α,求∠DOE的度数.
2021-2022学年苏科版七年级数学上册 寒假专题训练(角的计算)(解析)
一、选择题
1、已知OC平分∠AOB,∠AOB=64°,则∠AOC的度数是( )
A.64° B.32° C.128° D.不能计算
【答案】B
【分析】
直接根据角平分线的定义得出∠AOC=∠AOB,再计算即可.
【详解】
解:∵∠AOB=64°,OC平分∠AOB,
∴∠AOC=∠AOB=×64°=32°.
故选:B.
2、已知∠a=25,则∠a的补角的度数是( )
A.65° B.75° C.155° D.165°
【答案】C
【分析】
根据补角的定义得出∠A的补角是180°-∠a,代入求出即可.
【详解】
解:∵∠a =25°,
∴∠a的补角是180°-∠a =180°-25°=155°.
故选:C.
3、如果∠α=52°25′,则∠α的余角的度数为( )
A.38°25′ B.37°45′ C.37°35′ D.127°35′
【答案】C
【分析】
根据互余的两个角的和等于90°列式计算即可得解.
【详解】
解:∵∠α=52°25′,
则∠α的余角的度数=90°﹣52°25′=89°60'﹣52°25'=37°35′.
故选:C.
4、15点整时针与分针的夹角度数为( )
A.60° B.75° C.90° D.100°
【答案】C
【分析】
钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,15点整时,时针指到3上,分针指到12上,15点整时针和分针夹角是3份即可得出答案.
【详解】
解:15点整,时针和分针夹角是3份,每份30°,
故3×30°=90°.
故选:C.
5、将一副三角板按如图所示的方式放置,则∠AOB=( )
A.30° B.45° C.75° D.80°
【答案】C
【分析】
根据一幅直角三角板的度数有60°,45°,30°,90°,即可得到答案.
【详解】
根据题意,得:∠AOB=45°+30°=75°.
故选C.
6、如图,直线AB、CD相交于点O,OE平分∠AOD,若∠1=38°,则∠COE等于( )
A.66° B.76° C.109° D.144°
【答案】C
【分析】
根据邻补角的概念求出∠AOD,根据角平分线的定义求出∠DOE,再根据邻补角的概念计算,得到答案.
【详解】
解:∵∠1=38°,
∴∠AOD=180°﹣∠1=142°,
∵OE平分∠AOD,
∴∠DOE=∠AOD=71°,
∴∠COE=180°﹣∠DOE=109°,
故选:C.
7、如图,甲从处出发沿北偏东方向走到处,乙从处出发沿南偏西 方向走到处,则的度数是( )
A. B. C. D.
【答案】C
【分析】
根据题意得到∠EAD=∠DOF=90°,先求出∠BAD=30°,再根据∠BAC=∠EAD+∠DAF+∠CAF即可求解.
【详解】
解:如图,由题意得∠EAD=∠DOF=90°,
∵∠EAB=60°,
∴∠BAD=∠EAD-∠EAB=90°-60°=30°,
∴∠BAC=∠BAD+∠DAF+∠CAF=30°+90°+30°=120°.
故选:C
8、如图,将一副三角板的直角顶点重合摆放在桌面上,下列各组角中一定能互补的是( )
A.∠BCE和∠ACE B.∠ACD和∠ACE
C.∠DCB和∠ACE D.∠DCB和∠ACB
【答案】C
【分析】
分别将四个选项中的两个角相加,如果和为,那么这两个角互补.
【详解】
A选项、∵,
∴和不一定互补,故不符合题意;
B选项、∵,
∴和不一定互补,故不符合题意;
C选项、∵,
∴和互补,符合题意;
D选项、∵,
∴和不一定互补,故不符合题意;
故选:C.
9、如图,∠AOB=90°,∠BOC=15°,OC平分∠AOD,则∠BOD的度数是( )
A.75° B.60° C.65° D.55°
【答案】B
【分析】
先求出∠AOC,再根据角平分线的定义求出∠AOD,然后根据∠BOD=∠AOD﹣∠AOB代入数据进行计算即可得解.
【详解】
解:∵∠AOB=90°,∠BOC=15°,
∴∠AOC=∠AOB﹣∠BOC=90°﹣15°=75°,
∵OC平分∠AOD,
∴∠AOD=2∠AOC=2×75°=150°,
∴∠BOD=∠AOD﹣∠AOB=150°﹣90°=60°,
故选:B.
10、如图,已知是直角,OM平分,ON平分,则的度数是( )
A.30° B.45° C.50° D.60°
【答案】B
【分析】
由角平分线的定义可得,∠COM=∠AOC,∠NOC=∠BOC,再根据∠MON=∠MOC-∠NOC解答即可.
【详解】
∵OM平分,∴∠COM=∠AOC,
∵ON平分∠BOC,∴∠NOC=∠BOC,
∴∠MON=∠MOC-∠NOC= (∠AOC-∠BOC)=∠AOB=45°.
故选B.
二、填空题
11、如图,两直线交于点O,若∠1+∠2=76°,则∠1= 度.
【分析】直接利用对顶角的性质结合已知得出答案.
【解析】∵两直线交于点O,
∴∠1=∠2,
∵∠1+∠2=76°,
∴∠1=38°.
故答案为:38.
12、如图,直线a,b相交于点O,若∠1+∠2=220°,则∠3= .
【分析】根据对顶角相等可得∠1的度数,再利用邻补角互补可得答案.
【解析】∵∠1=∠2,∠1+∠2=220°,
∴∠1=∠2=110°,
∴∠3=180°﹣110°=70°,
故答案为:70°.
13、如图,直线,相交于点O,,,则的度数为__________.
【答案】110
【分析】
先根据对顶角相等求出∠DOB,进而结合即可求出∠EOB.
【详解】
解:∵∠1=35°,
∴∠DOB=∠1=35°,
又∵∠2=75°,
∴∠EOB=∠2+∠DOB=110°.
故答案为:110.
14、如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠BOD等于_____.
【答案】75°
【分析】
依据OD是∠AOC的平分线,即可得到∠AOC=2∠COD=50°,再根据OC是∠AOB的平分线,即可得到∠BOC=∠AOC=50°,进而得出∠BOD=75°.
【详解】
解:∵OD是∠AOC的平分线,且∠COD=25°,
∴∠AOC=2∠COD=50°,
又∵OC是∠AOB的平分线,
∴∠BOC=∠AOC=50°,
∴∠BOD=∠BOC+∠COD=50°+25°=75°,
故答案为:75°.
15、如图所示,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11,则∠AOB=_______.
【答案】20°
【分析】
由∠AOB+∠BOC=∠BOC+∠COD知∠AOB=∠COD,设∠AOB=2α,则∠AOD=11α,故∠AOB+∠BOC=5α=90°,解得α即可.
【详解】
解:∵∠AOB+∠BOC=∠BOC+∠COD,
∴∠AOB=∠COD,
设∠AOB=2α,
∵∠AOB:∠AOD=2:11,
∴∠AOB+∠BOC=9α=90°,
解得α=10°,
∴∠AOB=20°.
故答案为20°.
16、如图,AB、CD相交于点O,OB平分.若,则的度数是________.
【答案】
【分析】
根据对顶角相等可得出∠BOD的度数,根据角平分线的性质可得出∠DOE.
【详解】
解:∵∠AOC和∠BOD是对顶角,
∴∠BOD=∠AOC=30°,
∵OB平分∠DOE,
∴∠DOE=2∠BOD=60°.
故答案为:60°.
17、如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的平分线,则∠BAD的度数为___°.
【答案】80
【分析】
由∠BAE=110°,∠CAE=60°,可得∠BAC=110°﹣60°=50°,结合∠CAF=110°,可得∠BAF=110°+50°=160°,再由AD平分∠BAF即可得∠BAD=80°.
【详解】
∵∠BAE=110°,∠CAE=60°,
∴∠BAC=110°﹣60°=50°,
又∵∠CAF=110°,
∴∠BAF=110°+50°=160°,
又∵AD是∠BAF的角平分线,
∴∠BAD=∠BAF=×160°=80°.
故答案为:80.
18、如图,直线AB,CD相交于点O,OF平分∠BOD,OE平分∠COF,∠AOD:∠BOF=4:1,
则∠AOE= .
【分析】根据角平分线的定义得出∠BOD=2∠BOF,∠BOF=∠DOF,根据∠AOD:∠BOF=4:1求出∠AOD:∠BOD=4:2,根据邻补角互补求出∠AOD=120°,∠BOD=60°,求出∠AOC=60°,根据角平分线定义求出∠COE,再求出答案即可.
【解析】∵OF平分∠BOD,∴∠BOD=2∠BOF,∠BOF=∠DOF,
∵∠AOD:∠BOF=4:1,∴∠AOD:∠BOD=4:2,
∵∠AOD+∠BOD=180°,
∴∠AOD=120°,∠BOD=60°,∴∠AOC=∠BOD=60°,
∴∠BOF=∠DOF==30°,∴∠COF=180°﹣∠DOF=150°,
∵OE平分∠COF,∴∠COE=COF=,
∴∠AOE=∠AOC+∠COE=60°+75°=135°,
故答案为:135°.
三、解答题
19、如图:∠AOB=160°,OC是∠AOB的平分线,OD是∠COB的平分线,求∠COD的度数.
【答案】40°
【分析】
根据角平分线的定义得出∠COB=∠AOB,∠COD=∠COB,即可求出答案.
【详解】
解:∵OC是∠AOB的平分线,∠AOB=160°,
∴∠COB=∠AOB =×160°=80°,
又∵OD是∠COB的平分线,
∴∠COD=∠COB =×80°=40°.
20、如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC.求∠BOD的度数.
【分析】直接利用角平分线的定义结合对顶角的性质得出答案.
【解析】∵∠EOC=70°,OA平分∠EOC,
∴∠EOA=∠AOC=70°=35°,
∴∠BOD=∠AOC=35°.
21、如图,直线相交于点平分,求:
(1)的度数.
(2)的度数.
【答案】(1)140°;(2)40°
【分析】
(1)根据平角的定义可得,利用角平分线的定义可得,再根据平角的定义即可求解;
(2)直接利用对顶角相等即可求解.
【详解】
解:(1)∵∠,
∴,
∵OB平分,
∴,
∴;
(2)∵,
∴.
22、如图,已知直线AE, O 是直线AE上一点.OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=30°
(1)求∠AOC的度数;
(2)求∠COE的度数;
(3)求∠BOD的度数.
【答案】(1)60°;(2)120°;(3)90°
【分析】
(1)根据角平分线的定义求解即可;
(2)根据平角定义即可求解;
(3)根据角平分线的定义求得∠COD,进而可求得∠BOD的度数.
【详解】
解:(1)∵OB是∠AOC的平分线,∠AOB=30°,
∴∠BOC=∠AOB=30°,
∴∠AOC=2∠AOB=60°;
(2)∵∠AOC+∠COE=180°,
∴∠COE=180°﹣∠AOC=180°﹣60°=120°;
(3)∵OD是∠COE的平分线,
∴∠COD= ∠COE=60°,
∴∠BOD=∠COD+∠BOC=60°+30°=90°.
23、如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=65°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
【答案】(1)115°;(2)45°
【分析】
(1)根据角平分线的定义,得出∠EOC=∠BOE=65°,利用邻补角定义求出∠DOE即可;
(2)根据角平分线的定义,∠BOD:∠BOE=2:3,求出∠BOD,再根据对顶角可求出∠AOC,利用垂直,求出∠AOF.
【详解】
(1)∵OE平分∠BOC,∠BOE=65°,
∴∠EOC=∠BOE=65°,
∴∠DOE=180°-∠EOC=180°-65°=115°;
(2)∵OE平分∠BOC,
∴∠EOC=∠BOE,
∵∠BOD:∠BOE=2:3,
设∠BOD=x,则∠COE=∠BOE=,
∵∠COE+∠BOE+∠BOD=180°,
∴,
∴x=45°,
∵OF⊥CD,∠BOD=∠AOC,
∴∠BOD=∠AOC=45°,
∴∠COF=90°,
∴∠AOF=∠COF-∠AOC=90°-45°=45°.
24、如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
(1)图中∠AOD的补角是 ;∠BOD的余角是 .
(2)已知∠COD=40°,求∠COE的度数.
【答案】(1)∠BOD,∠COD;∠COE,∠AOE;(2)50°
【分析】
(1)根据“和为180°的两个角互为补角”、“和为90°的两个角互为余角”进行解答;
(2)∠AOB是平角,∠AOB=∠AOC+∠BOC以及角平分线的定义进行求解即可.
【详解】
(1)∵∠AOD+∠BOD=180°
∴∠BOD是∠AOD的补角;
∵OD平分∠BOC,OE平分∠AOC,
∴ ,
∴,
∴∠AOE和∠EOC是∠BOD的余角;∠COD和∠BOD是∠AOD的补角;
故答案为:∠BOD,∠COD;∠COE,∠AOE;
(2)解:∵OD平分∠BOC,∠COD=40°
∴∠BOC=2∠COD=80°
由题意可知,∠AOB是平角,∠AOB=∠AOC+∠BOC
∴∠AOC=∠AOB-∠BOC
=180°-80°
=100°
∵OE平分∠AOC,
∴∠COE=∠AOC=50°.
25、已知,如图直线与相交于点O,,过点O作射线,,.
(1)求度数;
(2)求的度数;
(3)直接写出图中所有与互补的角.
【答案】(1)60°(2)90°(3)、、
【分析】
(1)根据垂直的定义得到,由对顶角的性质得到,即可得出结论;
(2)根据平角的定义即可得出结论;
(3)根据补角的定义即可得出结论.
【详解】
解:(1)∵,
∴,
∵,
∴=60°;
(2)∵=60°,
∴;
(3)∵,
,
,
∴与互补的角为:、、.
26、如图,点O是直线AB上一点,OD,OE分别平分∠AOC和∠BOC.
(1)若∠AOC=40°,求∠DOE的度数.
(2)若∠AOC=α,求∠DOE的度数.
【答案】(1)90°;(2)90°.
【分析】
(1)根据∠AOC=40°,则可计算出∠BOC=140°,再根据角平分线的定义得到∠COD=∠AOC=20°,∠COE=∠BOC=70°,然后利用∠DOE=∠COD+∠COE进行计算,即可求∠DOE的度数;
(2)根据∠AOC=α,则可计算出∠BOC=180° α,再根据角平分线的定义得到∠COD=∠AOC=α,∠COE=∠BOC=90° α,然后利用∠DOE=∠COD+∠COE进行计算即可.
【详解】
解:(1)∵∠AOC=40°,
∴∠BOC=180° ∠AOC=140°.
∵OD,OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOC=×40°=20°,
∠COE=∠BOC=×140°=70°.
∴∠DOE=∠COD+∠COE=20°+70°=90°.
(2)∵∠AOC=α,
∴∠BOC=180° ∠AOC=180° α.
∵OD,OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOC=α,
∠COE=∠BOC=(180 α)=90° α.
∴∠DOE=∠COD+∠COE=α+(90° α)=90°.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
