第5章 平面直角坐标系 复习与测试(含解析)
文档属性
| 名称 | 第5章 平面直角坐标系 复习与测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 09:32:59 | ||
图片预览



文档简介
第5章复习与测试
一、选择题(每小题3分,共30分)
1.在平面直角坐标系中,点P(-3,4)到x轴的距离为( )
A.3 B.-3 C.4 D.-4
2.下列各点中,在第三象限的点是( )
A.(2,-4)
B.(2,4)
C.(-2,4)
D.(-2,-4)
3.坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的3倍.若A点在第二象限,则A点坐标( )
A.(-9,3) B.(-3,1) C.(-3,9) D.(9,3)
4.线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
A.(4,2) B.(﹣4,2) C.(﹣4,﹣2) D.(4,﹣2)
5.如果点P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0)
B.(0,-2)
C.(1,0)
D.(0,1)
6.如图所示,小手盖住的点的坐标可能为( )
A.(5,2)
B.(-6,3)
C.(-4,-6)
D.(3,-4)
7.如图,点A位于点O的( )方向上.
A南偏东35° B、北偏西65° C、南偏东65° D、南偏西65°
8.若a>0,b<-2,则点(a,b+2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知点P1(,3)和P2(2,)关于x轴对称,则的值为( )
A.0 B.-1 C.1 D.
10.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第63秒时,这个点所在位置的坐标是( )
A.(7,0) B.(0,7) C.(7,7) D.(6,0)
二、填空题(第16题4分,其他每小题2分,共20分)
11.点P(-2,3)关于原点的对称点的坐标是 .
12.点P(-3,5)到到y轴的距离是________.
13.将点A(2,1)向上平移3个单位长度得到点B的坐标是 .
14.平面直角坐标系中,已知点A(﹣1,﹣3)和点B(1,﹣2),则线段AB的长为 .
15.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,-5),A(4,0),则AD·BC=_______.
16.已知不同的两点A(2,n),B(m,-4)不重合.若线段AB∥x轴,且A、B到y轴距离相等,则m=________,n=________;若线段AB∥y轴,且A、B到x轴距离相等,则m=________,n=________.
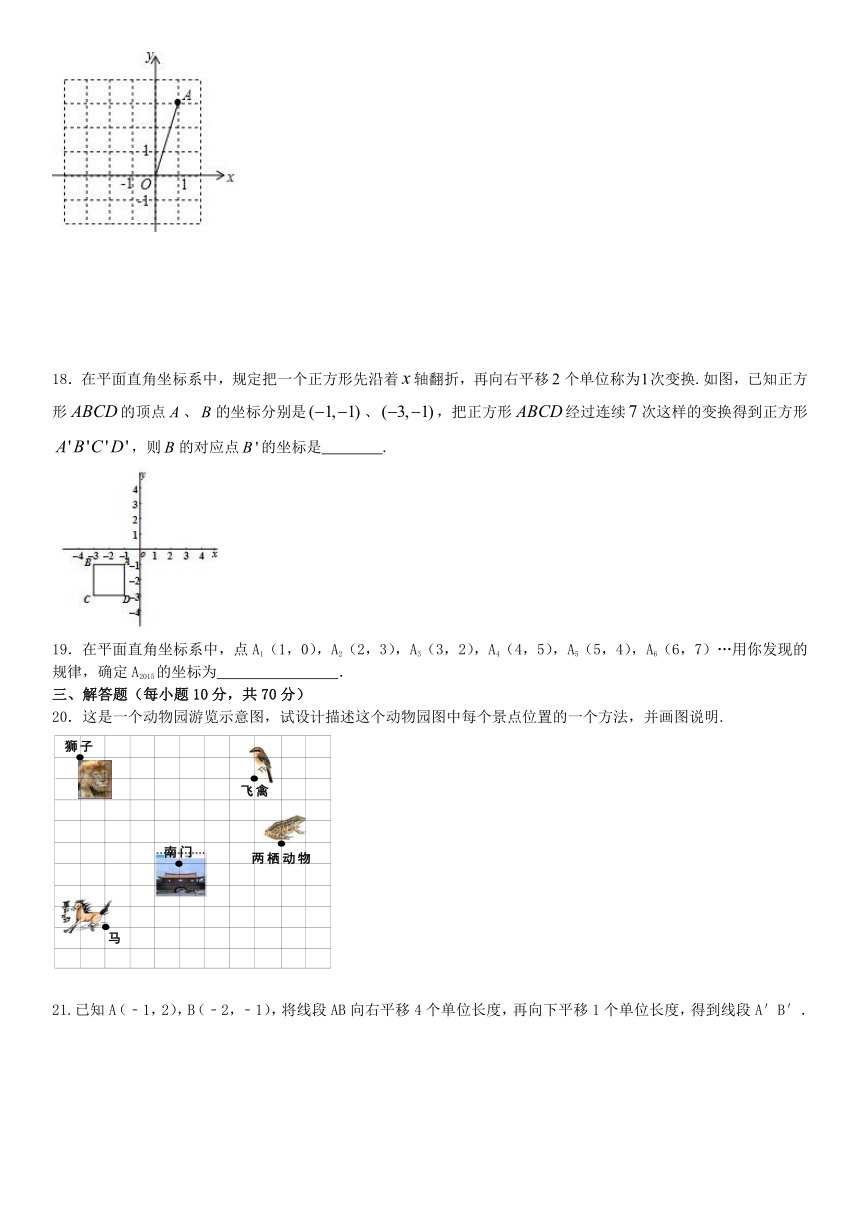
17.如图,在平面直角坐标系中,点A坐标为(1,3),将线段OA向左平移2个单位长度,得到线段O′A′,则点A的对应点A′的坐标为 .
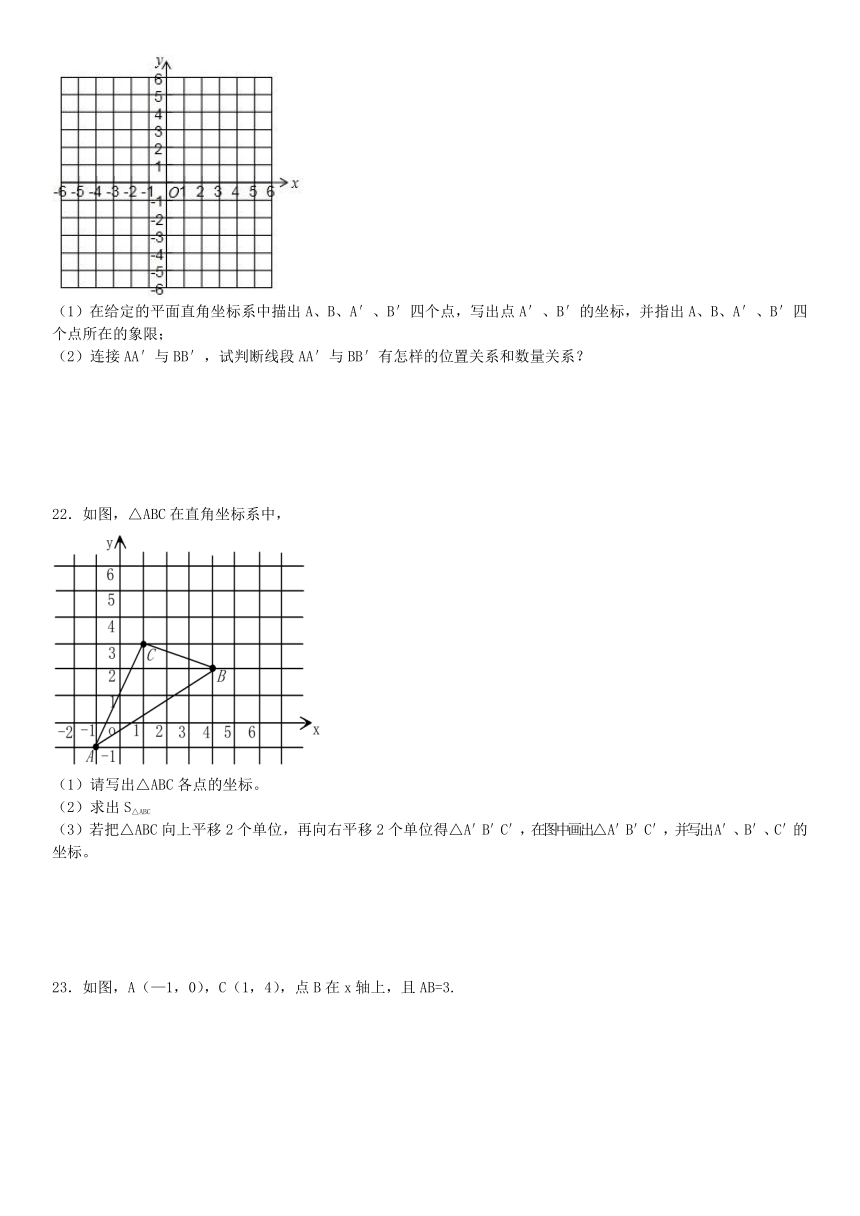
18.在平面直角坐标系中,规定把一个正方形先沿着轴翻折,再向右平移个单位称为次变换.如图,已知正方形的顶点、的坐标分别是、,把正方形经过连续次这样的变换得到正方形,则的对应点的坐标是 .
19.在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,2),A4(4,5),A5(5,4),A6(6,7)…用你发现的规律,确定A2015的坐标为 .
三、解答题(每小题10分,共70分)
20.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
21.已知A(﹣1,2),B(﹣2,﹣1),将线段AB向右平移4个单位长度,再向下平移1个单位长度,得到线段A′B′.
(1)在给定的平面直角坐标系中描出A、B、A′、B′四个点,写出点A′、B′的坐标,并指出A、B、A′、B′四个点所在的象限;
(2)连接AA′与BB′,试判断线段AA′与BB′有怎样的位置关系和数量关系?
22.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标。
23.如图,A(—1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积.
24.在直角坐标系中,长方形ABCD的边AB可表示为(-2,y)(-1≤y≤2),边AD可表示为(x,2)(-2≤x≤4).求:
(1)长方形各顶点的坐标;
(2)长方形ABCD的周长.
25.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:(+1,+4),从(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中,
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若图中另有两个格点M、N,且,,则应记作什么?
26.如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积.
(2)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
答案解析
一、选择题(每小题3分,共30分)
1.在平面直角坐标系中,点P(-3,4)到x轴的距离为( )
A.3 B.-3 C.4 D.-4
【答案】C
【解析】
试题分析:∵|4|=4,∴点P(﹣3,4)到x轴距离为4.故选C.
【难度】容易
2.下列各点中,在第三象限的点是( )
A.(2,-4)
B.(2,4)
C.(-2,4)
D.(-2,-4)
【答案】D
【解析】第三象限的点的横坐标和纵坐标都为负数,故选D.
【难度】容易
3.坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的3倍.若A点在第二象限,则A点坐标( )
A.(-9,3) B.(-3,1) C.(-3,9) D.(9,3)
【答案】A
【解析】
试题分析:∵点A在第二象限,A点到x轴的距离为3,A点到y轴的距离为到x轴距离的3倍,
∴点A的纵坐标为3,横坐标为-9,
∴点A的坐标为(-9,3).
故选A.
【难度】较易
4.线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
A.(4,2) B.(﹣4,2) C.(﹣4,﹣2) D.(4,﹣2)
【答案】D
【解析】
试题分析:根据坐标系可得M点坐标是(-4,-2),再根据关于y轴对称的点的坐标特点:纵坐标相等,横坐标互为相反数,故点M的对应点M′的坐标为(4,-2),
故选:D
【难度】一般
5.如果点P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0)
B.(0,-2)
C.(1,0)
D.(0,1)
【答案】B
【解析】因为y轴上的点的横坐标为0,所以m+3=0,解得m=-3.当m=-3时,2m+4=-2,故P(0,-2).
【难度】一般
6.如图所示,小手盖住的点的坐标可能为( )
A.(5,2)
B.(-6,3)
C.(-4,-6)
D.(3,-4)
【答案】D
【解析】因为小手盖住的点在第四限象,第四象限内的点的横坐标是正数,纵坐标是负数,故选D.
【难度】一般
7.如图,点A位于点O的( )方向上.
A南偏东35° B、北偏西65° C、南偏东65° D、南偏西65°
【答案】B
【解析】
试题分析:点A位于点O的北偏西65°的方向上.
故选B.
【难度】一般
8.若a>0,b<-2,则点(a,b+2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【解析】
试题分析:根据b<-2确定出b+2<0,然后根据各象限内点的坐标特征解答.
【难度】一般
9.已知点P1(,3)和P2(2,)关于x轴对称,则的值为( )
A.0 B.-1 C.1 D.
【答案】C
【解析】
试题分析:∵点P1(,3)和P2(2,)关于x轴对称,∴,,解得,,∴.故选C.
【难度】一般
10.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第63秒时,这个点所在位置的坐标是( )
A.(7,0) B.(0,7) C.(7,7) D.(6,0)
【答案】A
【解析】
3秒时到了(1,0);8秒时到了(0,2);15秒时到了(3,0);24秒到了(0,4);35秒到了(5,0);48秒到了(0,6);63秒到了(7,0);∴那么第63秒后质点所在位置的坐标是(7,0).
【难度】困难
二、填空题(第16题4分,其他每小题2分,共20分)
11.点P(-2,3)关于原点的对称点的坐标是 .
【答案】(2,-3)
【解析】
试题分析:根据平面直角坐标系的性质可知:关于原点对称时,横纵坐标均变为相反数,关于x轴对称,横坐标不变,纵坐标变为相反数,关于y轴对称,横坐标变为相反数,纵坐标不变,因此可知P关于原点对称的点的坐标为(2,-3).
【难度】容易
12.点P(-3,5)到到y轴的距离是________.
【答案】3
【解析】到y轴的距离是横坐标的绝对值.
【难度】容易
13.将点A(2,1)向上平移3个单位长度得到点B的坐标是 .
【答案】(2,4)
【解析】
试题分析:原来点的横坐标是2,纵坐标是1,向上平移3个单位长度得到新点的横坐标不变,纵坐标为1+3=4.即该坐标为(2,4).故答案填:(2,4).
【难度】一般
14.平面直角坐标系中,已知点A(﹣1,﹣3)和点B(1,﹣2),则线段AB的长为 .
【答案】
【解析】
试题分析:已知点A(﹣1,﹣3)和点B(1,﹣2),由勾股定理可得AB=.
【难度】一般
15.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,-5),A(4,0),则AD·BC=_______.
【答案】32
【解析】
试题分析:此题用面积法,由A,B,C点的坐标知道,B到x轴的距离是3,C到AO的距离是5,OA=4,∴△ABC的面积=△AOB的面积+△AOC的面积==6+10=16,∵AD⊥BC于D,∴=16,∴AD· BC= 32.
【难度】一般
16.已知不同的两点A(2,n),B(m,-4)不重合.若线段AB∥x轴,且A、B到y轴距离相等,则m=________,n=________;若线段AB∥y轴,且A、B到x轴距离相等,则m=________,n=________.
【答案】-2;-4;2;4
【解析】(1)因为线段AB∥x轴,A(2,n),B(m,-4),所以n=-4.又因为A、B到y轴距离相等且A、B不重合,所以m=-2.
(2)同(1)可知,m=2,n=4.
【难度】一般
17.如图,在平面直角坐标系中,点A坐标为(1,3),将线段OA向左平移2个单位长度,得到线段O′A′,则点A的对应点A′的坐标为 .
【答案】(﹣1,3)
【解析】
试题分析:根据点向左平移a个单位,坐标P(x,y) P(x﹣a,y)进行计算即可.
解:∵点A坐标为(1,3),
∴线段OA向左平移2个单位长度,点A的对应点A′的坐标为(1﹣2,3),
即(﹣1,3),
故答案为:(﹣1,3).
【难度】一般
18.在平面直角坐标系中,规定把一个正方形先沿着轴翻折,再向右平移个单位称为次变换.如图,已知正方形的顶点、的坐标分别是、,把正方形经过连续次这样的变换得到正方形,则的对应点的坐标是 .
【答案】
【解析】
试题分析:题目求的是经过变换后的对应点,故只考虑.第一次变换后,,第二次变换后,…可推理出经过七次变换,对应点的纵坐标为,而横坐标是,所以.
【难度】一般
19.在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,2),A4(4,5),A5(5,4),A6(6,7)…用你发现的规律,确定A2015的坐标为 .
【答案】(2015,2014).
【解析】
试题分析:设An(x,y),
当n=1时,A1(1,0),即x=n=1,y=1﹣1=0,
当n=2时,A2(2,3),即x=n=2,y=2+1=3;
当n=3时,A3(3,2),即x=n=3,y=3﹣1=2;
当n=4时,A4(4,5),即x=n=4,y=4+1=5;
…
以此类推可得当n为偶数,An(x,y)的坐标是(n,n+1),当n为奇数,An(x,y)的坐标是(n,n﹣1)
又因2015为奇数,所以点A2015的坐标为(2015,2014).
【难度】较难
三、解答题(每小题10分,共70分)
20.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
【答案】狮子(1,10);马(2,2);南门(5,5);飞禽(8,9);两栖动物(9,6).
【解析】
试题分析:适当建立平面直角坐标系,确定原点及各个景点位置坐标.
试题解析:如图:以左下角的点为原点建立平面直角坐标系,每格规定为一个单位长度,确定各景点的坐标:狮子(1,10);马(2,2);南门(5,5);飞禽(8,9);两栖动物(9,6).
【难度】较易
21.已知A(﹣1,2),B(﹣2,﹣1),将线段AB向右平移4个单位长度,再向下平移1个单位长度,得到线段A′B′.
(1)在给定的平面直角坐标系中描出A、B、A′、B′四个点,写出点A′、B′的坐标,并指出A、B、A′、B′四个点所在的象限;
(2)连接AA′与BB′,试判断线段AA′与BB′有怎样的位置关系和数量关系?
【答案】(1)A′(3,1),B′(2,﹣2),由图可知,点A在第二象限,点B在第三象限,点A′在第一象限,点B′在第四象限;(2)AA′∥BB′,AA′=BB′.
【解析】
试题分析:(1)已知出A、B两点的坐标,再根据平移的性质确定点A′、B′的坐标,连接A′B′即可,并根据图象确定各点所在的象限即可;
(2)连接AA′与BB′,观察这两条线段在坐标系中的位置,即可得出结论.
试题解析:解:(1)如图所示,A′(3,1),B′(2,﹣2).由图可知,点A在第二象限,点B在第三象限,点A′在第一象限,点B′在第四象限;
(2)由图可知,AA′∥BB′,AA′=BB′.
【难度】一般
22.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标。
【答案】(1)A(-1,-1) B(4,2) C(1,3);(2)7;(3)A′(1,1) B′ (6,4) C′(3,5)
【解析】
试题分析:(1)根据点在坐标系中的位置得出点的坐标;
利用补形法求出面积;
根据题意画出图形,然后得出点的坐标.
试题解析:(1)A(-1,-1) B(4,2) C(1,3)
(2)S△ABC=4×5-×4×2-×5×3-×3×1=7;
(3)如图所示:
A′(1,1) B′ (6,4) C′(3,5)
【难度】一般
23.如图,A(—1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积.
【答案】(1)B(2,0)或(-4,0);(2)6.
【解析】
试题分析:(1)由于点B在x轴上,所以纵坐标为0,又AB=3,所以B的坐标就可以确定了,根据坐标也就画出了图形;
(2)根据已知条件可以得到AB边上的高为4,然后利用三角形的面积公式就可以求出△ABC的面积.
试题解析:(1)∵点B在x轴上,
∴纵坐标为0,
又AB=3,
∴B(2,0)或(-4,0);
(2)S△ABC=×3×4=6.
【难度】一般
24.在直角坐标系中,长方形ABCD的边AB可表示为(-2,y)(-1≤y≤2),边AD可表示为(x,2)(-2≤x≤4).求:
(1)长方形各顶点的坐标;
(2)长方形ABCD的周长.
【答案】(1)A(-2,2),B(-2,-1),C(4,-1),D(4,2)(2)18
【解析】
试题分析:1)根据边AB、AD的公共点为A,首先求出点A的坐标,从而得到点B、D的坐标,再根据点B的纵坐标与点D的横坐标求出点C的坐标即可;(2)根据x、y的取值范围求出AB、AD的长度,再根据长方形的周长公式列式进行计算即可得解.
试题解析::(1)∵边AB可表示为(-2,y),边AD可表示为(x,2),
∴点A的坐标为(-2,2),
∵-1≤y≤2,∴点B的坐标为(-2,-1),
∵-2≤x≤4,∴点D的坐标为(4,2),
∵四边形ABCD是长方形,∴点C的坐标为(4,-1);
(2)∵A(-2,2),B(-2,-1),D(4,2),
∴AB=2-(-1)=2+1=3,AD=4-(-2)=4+2=6,
∴长方形ABCD的周长=2(3+6)=18.
【难度】一般
25.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:(+1,+4),从(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中,
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若图中另有两个格点M、N,且,,则应记作什么?
【答案】(1)+2,0 ; D , 2;(2)10;(3)( 2, 2)
【解析】
试题分析:(1)根据规定及实例可知B→C记为(1,-2)C→D记为(2,1);;
(2)根据点的运动路径,表示出运动的距离,相加即可得到行走的总路径长;(3)根据M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),可得5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,所以点A向右走2个格点,向上走2个格点到点N.
试题解析:(1)∵规定:向上向右走为正,向下向左走为负
∴B→C记为(+2,0)C→D记为(+1,﹣2);
(2)据已知条件可知:A→B表示为:(1,4),B→C记为(2,0),C→D记为(1,﹣2);∴该甲虫走过的路线长为1+4+2+1+2=10.
(3)∵M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),
∴5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,
∴点A向右走2个格点,向上走2个格点到点N,
∴N→A应记为(﹣2,﹣2).
【难度】一般
26.如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积.
(2)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
【答案】(1)4;(2)存在.(0,3),(0,﹣1);(3)45°
【解析】
试题分析:(1)根据非负数的性质求出a,b的值,进而得出A(﹣2,0),C(2,2),B(2,0),然后根据三角形面积公式计算S△ABC;
(2)如图③,AC交y轴于Q,先确定Q(0,1),设P(0,t),利用S△PAC=S△APQ+S△CPQ=S△ABC得出关于t的方程,然后解方程求出t即可得到P点坐标;
(3)如图②,作EM∥AC,然后根据平行线的性质和角的平分线,得出∠AED=(∠CAB+∠ODB),而由AC∥BD得到∠CAB=∠OBD,于是∠CAB+∠ODB=∠OBD+∠ODB=90°,则∠AED=45°.
试题解析:(1)∵(a+2)2+=0,
∴a+2=0,b﹣2=0,解得a=﹣2,b=2,
∴A(﹣2,0),C(2,2),
∵CB⊥x轴,
∴B(2,0),
∴S△ABC=×(2+2)×2=4;
(2)存在.
如下图,
AC交y轴于Q,则Q(0,1),
设P(0,t),
∵S△PAC=S△APQ+S△CPQ=S△ABC,
∴ |t﹣1| 2+ |t﹣1| 2=4,解得t=3或t=﹣1,
∴P点坐标为(0,3),(0,﹣1);
(3)作EF∥AC,如下图,
∵AC∥BD,
∴AC∥EF∥BD,
∴∠CAE=∠AEF,∠BDE=∠DEF,
∴∠AED=∠CAE+∠BDE,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠CAE=∠CAB,∠BDE=∠ODB,
∴∠AED=(∠CAB+∠ODB),
∵AC∥BD,
∴∠CAB=∠OBD,
∴∠CAB+∠ODB=∠OBD+∠ODB=90°,
∴∠AED=×90°=45°.
【难度】较难
一、选择题(每小题3分,共30分)
1.在平面直角坐标系中,点P(-3,4)到x轴的距离为( )
A.3 B.-3 C.4 D.-4
2.下列各点中,在第三象限的点是( )
A.(2,-4)
B.(2,4)
C.(-2,4)
D.(-2,-4)
3.坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的3倍.若A点在第二象限,则A点坐标( )
A.(-9,3) B.(-3,1) C.(-3,9) D.(9,3)
4.线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
A.(4,2) B.(﹣4,2) C.(﹣4,﹣2) D.(4,﹣2)
5.如果点P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0)
B.(0,-2)
C.(1,0)
D.(0,1)
6.如图所示,小手盖住的点的坐标可能为( )
A.(5,2)
B.(-6,3)
C.(-4,-6)
D.(3,-4)
7.如图,点A位于点O的( )方向上.
A南偏东35° B、北偏西65° C、南偏东65° D、南偏西65°
8.若a>0,b<-2,则点(a,b+2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.已知点P1(,3)和P2(2,)关于x轴对称,则的值为( )
A.0 B.-1 C.1 D.
10.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第63秒时,这个点所在位置的坐标是( )
A.(7,0) B.(0,7) C.(7,7) D.(6,0)
二、填空题(第16题4分,其他每小题2分,共20分)
11.点P(-2,3)关于原点的对称点的坐标是 .
12.点P(-3,5)到到y轴的距离是________.
13.将点A(2,1)向上平移3个单位长度得到点B的坐标是 .
14.平面直角坐标系中,已知点A(﹣1,﹣3)和点B(1,﹣2),则线段AB的长为 .
15.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,-5),A(4,0),则AD·BC=_______.
16.已知不同的两点A(2,n),B(m,-4)不重合.若线段AB∥x轴,且A、B到y轴距离相等,则m=________,n=________;若线段AB∥y轴,且A、B到x轴距离相等,则m=________,n=________.
17.如图,在平面直角坐标系中,点A坐标为(1,3),将线段OA向左平移2个单位长度,得到线段O′A′,则点A的对应点A′的坐标为 .
18.在平面直角坐标系中,规定把一个正方形先沿着轴翻折,再向右平移个单位称为次变换.如图,已知正方形的顶点、的坐标分别是、,把正方形经过连续次这样的变换得到正方形,则的对应点的坐标是 .
19.在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,2),A4(4,5),A5(5,4),A6(6,7)…用你发现的规律,确定A2015的坐标为 .
三、解答题(每小题10分,共70分)
20.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
21.已知A(﹣1,2),B(﹣2,﹣1),将线段AB向右平移4个单位长度,再向下平移1个单位长度,得到线段A′B′.
(1)在给定的平面直角坐标系中描出A、B、A′、B′四个点,写出点A′、B′的坐标,并指出A、B、A′、B′四个点所在的象限;
(2)连接AA′与BB′,试判断线段AA′与BB′有怎样的位置关系和数量关系?
22.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标。
23.如图,A(—1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积.
24.在直角坐标系中,长方形ABCD的边AB可表示为(-2,y)(-1≤y≤2),边AD可表示为(x,2)(-2≤x≤4).求:
(1)长方形各顶点的坐标;
(2)长方形ABCD的周长.
25.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:(+1,+4),从(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中,
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若图中另有两个格点M、N,且,,则应记作什么?
26.如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积.
(2)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
答案解析
一、选择题(每小题3分,共30分)
1.在平面直角坐标系中,点P(-3,4)到x轴的距离为( )
A.3 B.-3 C.4 D.-4
【答案】C
【解析】
试题分析:∵|4|=4,∴点P(﹣3,4)到x轴距离为4.故选C.
【难度】容易
2.下列各点中,在第三象限的点是( )
A.(2,-4)
B.(2,4)
C.(-2,4)
D.(-2,-4)
【答案】D
【解析】第三象限的点的横坐标和纵坐标都为负数,故选D.
【难度】容易
3.坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的3倍.若A点在第二象限,则A点坐标( )
A.(-9,3) B.(-3,1) C.(-3,9) D.(9,3)
【答案】A
【解析】
试题分析:∵点A在第二象限,A点到x轴的距离为3,A点到y轴的距离为到x轴距离的3倍,
∴点A的纵坐标为3,横坐标为-9,
∴点A的坐标为(-9,3).
故选A.
【难度】较易
4.线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
A.(4,2) B.(﹣4,2) C.(﹣4,﹣2) D.(4,﹣2)
【答案】D
【解析】
试题分析:根据坐标系可得M点坐标是(-4,-2),再根据关于y轴对称的点的坐标特点:纵坐标相等,横坐标互为相反数,故点M的对应点M′的坐标为(4,-2),
故选:D
【难度】一般
5.如果点P(m+3,2m+4)在y轴上,那么点P的坐标是( )
A.(-2,0)
B.(0,-2)
C.(1,0)
D.(0,1)
【答案】B
【解析】因为y轴上的点的横坐标为0,所以m+3=0,解得m=-3.当m=-3时,2m+4=-2,故P(0,-2).
【难度】一般
6.如图所示,小手盖住的点的坐标可能为( )
A.(5,2)
B.(-6,3)
C.(-4,-6)
D.(3,-4)
【答案】D
【解析】因为小手盖住的点在第四限象,第四象限内的点的横坐标是正数,纵坐标是负数,故选D.
【难度】一般
7.如图,点A位于点O的( )方向上.
A南偏东35° B、北偏西65° C、南偏东65° D、南偏西65°
【答案】B
【解析】
试题分析:点A位于点O的北偏西65°的方向上.
故选B.
【难度】一般
8.若a>0,b<-2,则点(a,b+2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【解析】
试题分析:根据b<-2确定出b+2<0,然后根据各象限内点的坐标特征解答.
【难度】一般
9.已知点P1(,3)和P2(2,)关于x轴对称,则的值为( )
A.0 B.-1 C.1 D.
【答案】C
【解析】
试题分析:∵点P1(,3)和P2(2,)关于x轴对称,∴,,解得,,∴.故选C.
【难度】一般
10.一个点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动:(0,0)→(0,1)→(1,1)→(1,0)→…,且每秒移动一个单位,那么第63秒时,这个点所在位置的坐标是( )
A.(7,0) B.(0,7) C.(7,7) D.(6,0)
【答案】A
【解析】
3秒时到了(1,0);8秒时到了(0,2);15秒时到了(3,0);24秒到了(0,4);35秒到了(5,0);48秒到了(0,6);63秒到了(7,0);∴那么第63秒后质点所在位置的坐标是(7,0).
【难度】困难
二、填空题(第16题4分,其他每小题2分,共20分)
11.点P(-2,3)关于原点的对称点的坐标是 .
【答案】(2,-3)
【解析】
试题分析:根据平面直角坐标系的性质可知:关于原点对称时,横纵坐标均变为相反数,关于x轴对称,横坐标不变,纵坐标变为相反数,关于y轴对称,横坐标变为相反数,纵坐标不变,因此可知P关于原点对称的点的坐标为(2,-3).
【难度】容易
12.点P(-3,5)到到y轴的距离是________.
【答案】3
【解析】到y轴的距离是横坐标的绝对值.
【难度】容易
13.将点A(2,1)向上平移3个单位长度得到点B的坐标是 .
【答案】(2,4)
【解析】
试题分析:原来点的横坐标是2,纵坐标是1,向上平移3个单位长度得到新点的横坐标不变,纵坐标为1+3=4.即该坐标为(2,4).故答案填:(2,4).
【难度】一般
14.平面直角坐标系中,已知点A(﹣1,﹣3)和点B(1,﹣2),则线段AB的长为 .
【答案】
【解析】
试题分析:已知点A(﹣1,﹣3)和点B(1,﹣2),由勾股定理可得AB=.
【难度】一般
15.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,-5),A(4,0),则AD·BC=_______.
【答案】32
【解析】
试题分析:此题用面积法,由A,B,C点的坐标知道,B到x轴的距离是3,C到AO的距离是5,OA=4,∴△ABC的面积=△AOB的面积+△AOC的面积==6+10=16,∵AD⊥BC于D,∴=16,∴AD· BC= 32.
【难度】一般
16.已知不同的两点A(2,n),B(m,-4)不重合.若线段AB∥x轴,且A、B到y轴距离相等,则m=________,n=________;若线段AB∥y轴,且A、B到x轴距离相等,则m=________,n=________.
【答案】-2;-4;2;4
【解析】(1)因为线段AB∥x轴,A(2,n),B(m,-4),所以n=-4.又因为A、B到y轴距离相等且A、B不重合,所以m=-2.
(2)同(1)可知,m=2,n=4.
【难度】一般
17.如图,在平面直角坐标系中,点A坐标为(1,3),将线段OA向左平移2个单位长度,得到线段O′A′,则点A的对应点A′的坐标为 .
【答案】(﹣1,3)
【解析】
试题分析:根据点向左平移a个单位,坐标P(x,y) P(x﹣a,y)进行计算即可.
解:∵点A坐标为(1,3),
∴线段OA向左平移2个单位长度,点A的对应点A′的坐标为(1﹣2,3),
即(﹣1,3),
故答案为:(﹣1,3).
【难度】一般
18.在平面直角坐标系中,规定把一个正方形先沿着轴翻折,再向右平移个单位称为次变换.如图,已知正方形的顶点、的坐标分别是、,把正方形经过连续次这样的变换得到正方形,则的对应点的坐标是 .
【答案】
【解析】
试题分析:题目求的是经过变换后的对应点,故只考虑.第一次变换后,,第二次变换后,…可推理出经过七次变换,对应点的纵坐标为,而横坐标是,所以.
【难度】一般
19.在平面直角坐标系中,点A1(1,0),A2(2,3),A3(3,2),A4(4,5),A5(5,4),A6(6,7)…用你发现的规律,确定A2015的坐标为 .
【答案】(2015,2014).
【解析】
试题分析:设An(x,y),
当n=1时,A1(1,0),即x=n=1,y=1﹣1=0,
当n=2时,A2(2,3),即x=n=2,y=2+1=3;
当n=3时,A3(3,2),即x=n=3,y=3﹣1=2;
当n=4时,A4(4,5),即x=n=4,y=4+1=5;
…
以此类推可得当n为偶数,An(x,y)的坐标是(n,n+1),当n为奇数,An(x,y)的坐标是(n,n﹣1)
又因2015为奇数,所以点A2015的坐标为(2015,2014).
【难度】较难
三、解答题(每小题10分,共70分)
20.这是一个动物园游览示意图,试设计描述这个动物园图中每个景点位置的一个方法,并画图说明.
【答案】狮子(1,10);马(2,2);南门(5,5);飞禽(8,9);两栖动物(9,6).
【解析】
试题分析:适当建立平面直角坐标系,确定原点及各个景点位置坐标.
试题解析:如图:以左下角的点为原点建立平面直角坐标系,每格规定为一个单位长度,确定各景点的坐标:狮子(1,10);马(2,2);南门(5,5);飞禽(8,9);两栖动物(9,6).
【难度】较易
21.已知A(﹣1,2),B(﹣2,﹣1),将线段AB向右平移4个单位长度,再向下平移1个单位长度,得到线段A′B′.
(1)在给定的平面直角坐标系中描出A、B、A′、B′四个点,写出点A′、B′的坐标,并指出A、B、A′、B′四个点所在的象限;
(2)连接AA′与BB′,试判断线段AA′与BB′有怎样的位置关系和数量关系?
【答案】(1)A′(3,1),B′(2,﹣2),由图可知,点A在第二象限,点B在第三象限,点A′在第一象限,点B′在第四象限;(2)AA′∥BB′,AA′=BB′.
【解析】
试题分析:(1)已知出A、B两点的坐标,再根据平移的性质确定点A′、B′的坐标,连接A′B′即可,并根据图象确定各点所在的象限即可;
(2)连接AA′与BB′,观察这两条线段在坐标系中的位置,即可得出结论.
试题解析:解:(1)如图所示,A′(3,1),B′(2,﹣2).由图可知,点A在第二象限,点B在第三象限,点A′在第一象限,点B′在第四象限;
(2)由图可知,AA′∥BB′,AA′=BB′.
【难度】一般
22.如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标。
【答案】(1)A(-1,-1) B(4,2) C(1,3);(2)7;(3)A′(1,1) B′ (6,4) C′(3,5)
【解析】
试题分析:(1)根据点在坐标系中的位置得出点的坐标;
利用补形法求出面积;
根据题意画出图形,然后得出点的坐标.
试题解析:(1)A(-1,-1) B(4,2) C(1,3)
(2)S△ABC=4×5-×4×2-×5×3-×3×1=7;
(3)如图所示:
A′(1,1) B′ (6,4) C′(3,5)
【难度】一般
23.如图,A(—1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积.
【答案】(1)B(2,0)或(-4,0);(2)6.
【解析】
试题分析:(1)由于点B在x轴上,所以纵坐标为0,又AB=3,所以B的坐标就可以确定了,根据坐标也就画出了图形;
(2)根据已知条件可以得到AB边上的高为4,然后利用三角形的面积公式就可以求出△ABC的面积.
试题解析:(1)∵点B在x轴上,
∴纵坐标为0,
又AB=3,
∴B(2,0)或(-4,0);
(2)S△ABC=×3×4=6.
【难度】一般
24.在直角坐标系中,长方形ABCD的边AB可表示为(-2,y)(-1≤y≤2),边AD可表示为(x,2)(-2≤x≤4).求:
(1)长方形各顶点的坐标;
(2)长方形ABCD的周长.
【答案】(1)A(-2,2),B(-2,-1),C(4,-1),D(4,2)(2)18
【解析】
试题分析:1)根据边AB、AD的公共点为A,首先求出点A的坐标,从而得到点B、D的坐标,再根据点B的纵坐标与点D的横坐标求出点C的坐标即可;(2)根据x、y的取值范围求出AB、AD的长度,再根据长方形的周长公式列式进行计算即可得解.
试题解析::(1)∵边AB可表示为(-2,y),边AD可表示为(x,2),
∴点A的坐标为(-2,2),
∵-1≤y≤2,∴点B的坐标为(-2,-1),
∵-2≤x≤4,∴点D的坐标为(4,2),
∵四边形ABCD是长方形,∴点C的坐标为(4,-1);
(2)∵A(-2,2),B(-2,-1),D(4,2),
∴AB=2-(-1)=2+1=3,AD=4-(-2)=4+2=6,
∴长方形ABCD的周长=2(3+6)=18.
【难度】一般
25.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:(+1,+4),从(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中,
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若图中另有两个格点M、N,且,,则应记作什么?
【答案】(1)+2,0 ; D , 2;(2)10;(3)( 2, 2)
【解析】
试题分析:(1)根据规定及实例可知B→C记为(1,-2)C→D记为(2,1);;
(2)根据点的运动路径,表示出运动的距离,相加即可得到行走的总路径长;(3)根据M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),可得5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,所以点A向右走2个格点,向上走2个格点到点N.
试题解析:(1)∵规定:向上向右走为正,向下向左走为负
∴B→C记为(+2,0)C→D记为(+1,﹣2);
(2)据已知条件可知:A→B表示为:(1,4),B→C记为(2,0),C→D记为(1,﹣2);∴该甲虫走过的路线长为1+4+2+1+2=10.
(3)∵M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),
∴5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,
∴点A向右走2个格点,向上走2个格点到点N,
∴N→A应记为(﹣2,﹣2).
【难度】一般
26.如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积.
(2)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
【答案】(1)4;(2)存在.(0,3),(0,﹣1);(3)45°
【解析】
试题分析:(1)根据非负数的性质求出a,b的值,进而得出A(﹣2,0),C(2,2),B(2,0),然后根据三角形面积公式计算S△ABC;
(2)如图③,AC交y轴于Q,先确定Q(0,1),设P(0,t),利用S△PAC=S△APQ+S△CPQ=S△ABC得出关于t的方程,然后解方程求出t即可得到P点坐标;
(3)如图②,作EM∥AC,然后根据平行线的性质和角的平分线,得出∠AED=(∠CAB+∠ODB),而由AC∥BD得到∠CAB=∠OBD,于是∠CAB+∠ODB=∠OBD+∠ODB=90°,则∠AED=45°.
试题解析:(1)∵(a+2)2+=0,
∴a+2=0,b﹣2=0,解得a=﹣2,b=2,
∴A(﹣2,0),C(2,2),
∵CB⊥x轴,
∴B(2,0),
∴S△ABC=×(2+2)×2=4;
(2)存在.
如下图,
AC交y轴于Q,则Q(0,1),
设P(0,t),
∵S△PAC=S△APQ+S△CPQ=S△ABC,
∴ |t﹣1| 2+ |t﹣1| 2=4,解得t=3或t=﹣1,
∴P点坐标为(0,3),(0,﹣1);
(3)作EF∥AC,如下图,
∵AC∥BD,
∴AC∥EF∥BD,
∴∠CAE=∠AEF,∠BDE=∠DEF,
∴∠AED=∠CAE+∠BDE,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠CAE=∠CAB,∠BDE=∠ODB,
∴∠AED=(∠CAB+∠ODB),
∵AC∥BD,
∴∠CAB=∠OBD,
∴∠CAB+∠ODB=∠OBD+∠ODB=90°,
∴∠AED=×90°=45°.
【难度】较难
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
