第6章 一次函数 复习与测试(含解析)
文档属性
| 名称 | 第6章 一次函数 复习与测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 590.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 09:41:07 | ||
图片预览



文档简介
第6章复习与测试
一、选择题(每小题3分,共30分)
1.若函数是一次函数,则应满足的条件是( )
A.且 B.且
C.且 D.且
2.直线y=2x经过平移可以得到直线y=2x-2的是
A.向左平移2个单位 B.向右平移2个单位
C.向下平移2个单位 D.向上平移 2个单位
3.已知正比例函数y=kx(k≠0)的图象经过点(1,-2),则这个正比例函数的解析式为( )
A.y=2x B.y= 2x C.y=x D.y= x
4.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )
A.
B.
C.
D.
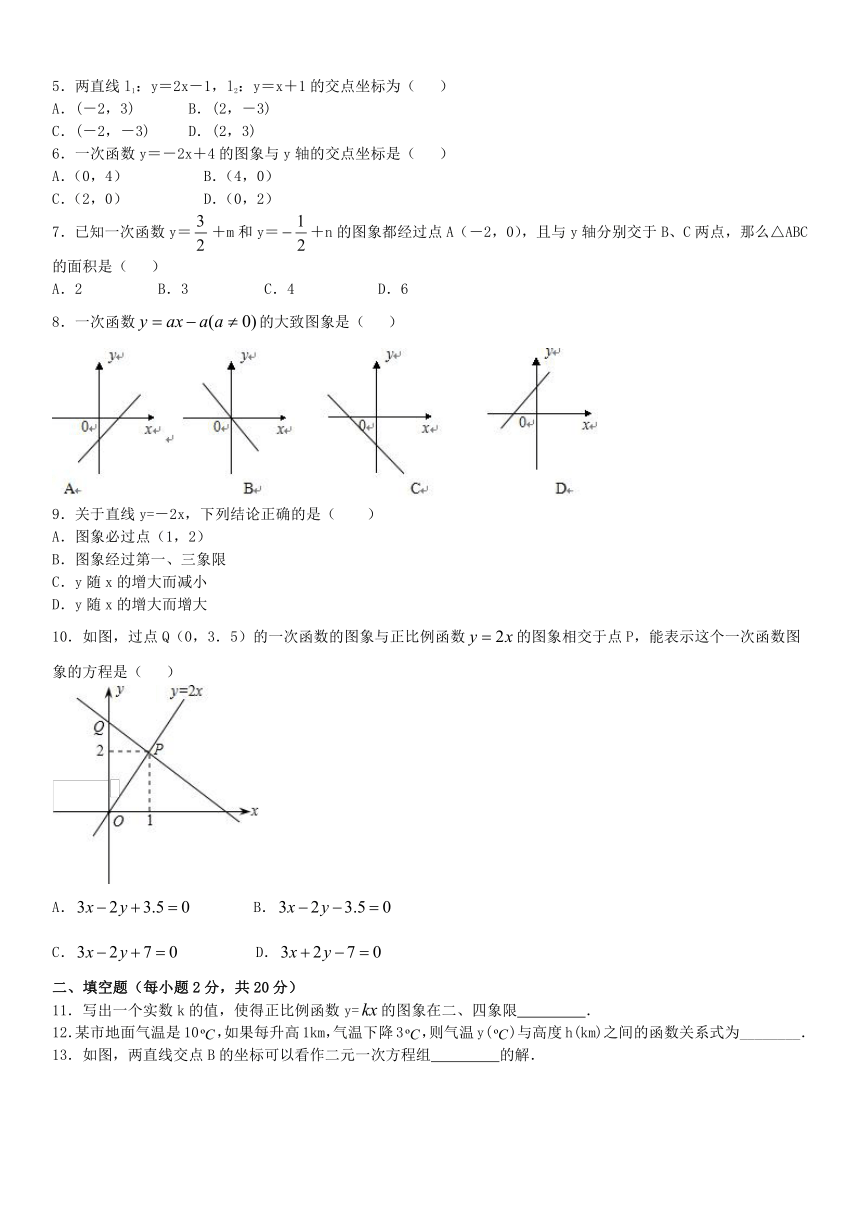
5.两直线l1:y=2x-1,l2:y=x+1的交点坐标为( )
A.(-2,3) B.(2,-3)
C.(-2,-3) D.(2,3)
6.一次函数y=-2x+4的图象与y轴的交点坐标是( )
A.(0,4) B.(4,0)
C.(2,0) D.(0,2)
7.已知一次函数y=+m和y=+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.6
8.一次函数的大致图象是( )
9.关于直线y=-2x,下列结论正确的是( )
A.图象必过点(1,2)
B.图象经过第一、三象限
C.y随x的增大而减小
D.y随x的增大而增大
10.如图,过点Q(0,3.5)的一次函数的图象与正比例函数的图象相交于点P,能表示这个一次函数图象的方程是( )
A. B.
C. D.
二、填空题(每小题2分,共20分)
11.写出一个实数k的值,使得正比例函数y=的图象在二、四象限 .
12.某市地面气温是10,如果每升高1km,气温下降3,则气温y()与高度h(km)之间的函数关系式为________.
13.如图,两直线交点B的坐标可以看作二元一次方程组 的解.
14.已知一次函数y=kx+b的图象如图所示,当x<﹣1时,y的取值范围是 .
15.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶 千米.
16.已知一次函数与两个坐标轴围成的三角形面积为4,则________.
17.点P(3,)、Q(,)在一次函数的图象上,则的大小关系是 .
18.下表给出的是关于某个一次函数的自变量x及其对应的函数值y的若干信息.请你根据表格中的相关数据计算:m+2n= .
19.如图,直线y=﹣x+b与直线y=2x﹣3相交于点P(m,1),则不等式﹣x+b>2x﹣3的解集为________.
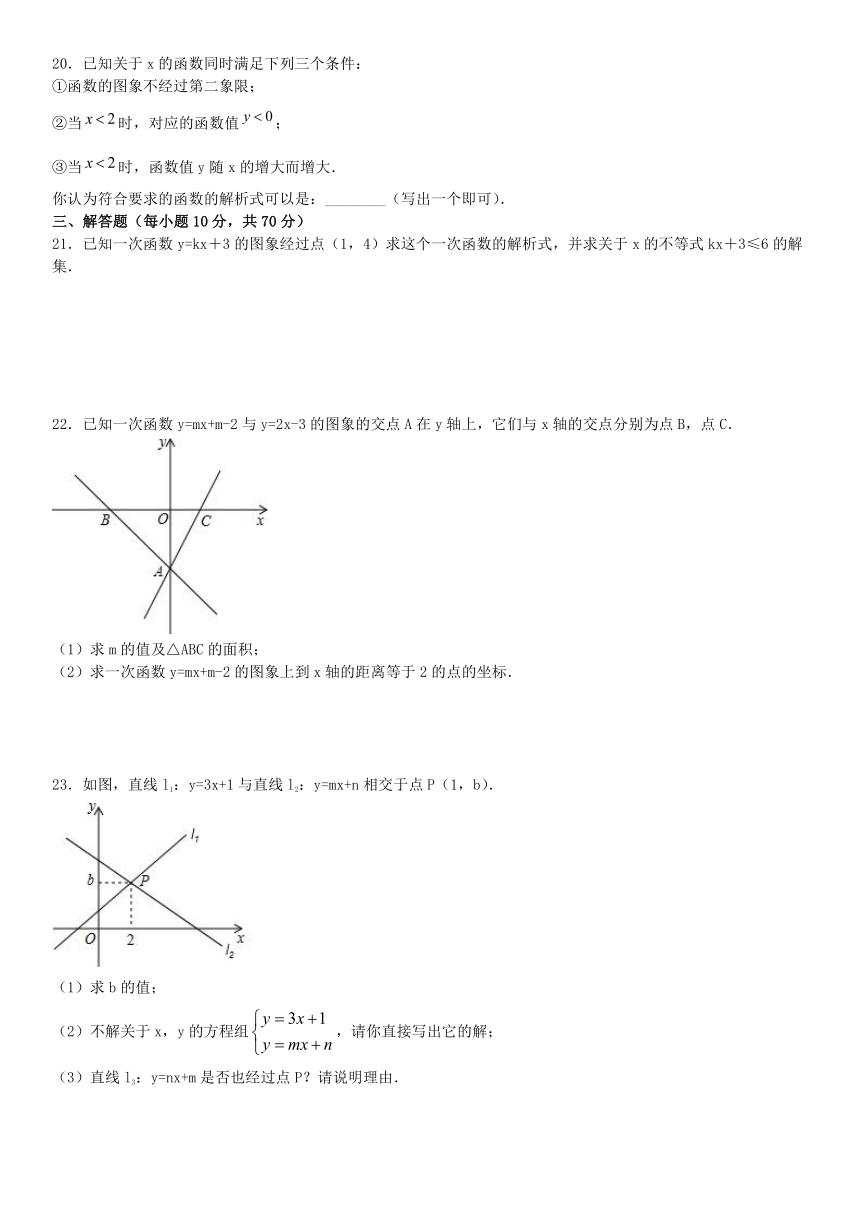
20.已知关于x的函数同时满足下列三个条件:
①函数的图象不经过第二象限;
②当时,对应的函数值;
③当时,函数值y随x的增大而增大.
你认为符合要求的函数的解析式可以是:________(写出一个即可).
三、解答题(每小题10分,共70分)
21.已知一次函数y=kx+3的图象经过点(1,4)求这个一次函数的解析式,并求关于x的不等式kx+3≤6的解集.
22.已知一次函数y=mx+m-2与y=2x-3的图象的交点A在y轴上,它们与x轴的交点分别为点B,点C.
(1)求m的值及△ABC的面积;
(2)求一次函数y=mx+m-2的图象上到x轴的距离等于2的点的坐标.
23.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组,请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
24.小丽一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干h后,途中在加油站加油若干L.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.
25.某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
A地 B地 C地
运费(元/件) 20 10 15
(1)设运往A地的水仙花x(件),总运费为y(元),试写出y与x的函数关系式;
(2)若总运费不超过12000元,最多可运往A地的水仙花多少件?
26.某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
甲(kg) 乙(kg) 件数(件)
A 5x x
B 4(40-x) 40-x
(2)安排生产A、B两种产品的件数有几种方案?试说明理由;
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
27.如图,在平面直角坐标系中,点A,B在第一象限,AB∥x轴,AB=2,点Q(6,0),根据图象回答:
(1)点B的坐标是 ;
(2)分别求出OA,BC所在直线的解析式;
(3)P是一动点,在折线OABC上沿O→A→B→C运动,不与O、C重合,点P(x,y),△OPQ的面积为S,求S与x的函数关系式,并指出自变量x的取值范围;
(4)在给出的坐标系中画出S随x变化的函数图象.
答案解析
一、选择题(每小题3分,共30分)
1.若函数是一次函数,则应满足的条件是( )
A.且 B.且
C.且 D.且
【答案】C
【解析】∵ 函数是一次函数,∴ 解得故选C.
【难度】容易
2.直线y=2x经过平移可以得到直线y=2x-2的是
A.向左平移2个单位 B.向右平移2个单位
C.向下平移2个单位 D.向上平移 2个单位
【答案】C
【解析】
试题分析:根据上加下减的平移原则,直线y=2x-2可以看作是由直线y=2x向下平移2个单位得到的;
故选C.
【难度】较易
3.已知正比例函数y=kx(k≠0)的图象经过点(1,-2),则这个正比例函数的解析式为( )
A.y=2x B.y= 2x C.y=x D.y= x
【答案】B
【解析】利用待定系数法把(1,-2)代入正比例函数y=kx中计算出k即可得到解析式.
解:∵正比例函数y=kx经过点(1,-2),
∴-2=1 k,
解得:k=-2,
∴这个正比例函数的解析式为:y=-2x.
故选B.
【难度】较易
4.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )
A.
B.
C.
D.
【答案】C
【解析】分三段讨论,①两车从开始到相遇,这段时间两车距迅速减小,②相遇后向相反方向行驶至特快到达甲地,这段时间两车距迅速增加,③特快到达甲地至快车到达乙地,这段时间两车距缓慢增大,结合实际选符合的图象即可.
解:①两车从开始到相遇,这段时间两车距迅速减小;
②相遇后向相反方向行驶至特快到达甲地,这段时间两车距迅速增加;
③特快到达甲地至快车到达乙地,这段时间两车距缓慢增大;
结合图象可得C选项符合题意.
故选C.
【难度】一般
5.两直线l1:y=2x-1,l2:y=x+1的交点坐标为( )
A.(-2,3) B.(2,-3)
C.(-2,-3) D.(2,3)
【答案】D
【解析】∵方程组的解是
∴选D.
【难度】一般
6.一次函数y=-2x+4的图象与y轴的交点坐标是( )
A.(0,4) B.(4,0)
C.(2,0) D.(0,2)
【答案】A
【解析】 令x=0,得y=-2×0+4=4,
则函数图象与y轴的交点坐标是(0,4).
【难度】一般
7.已知一次函数y=+m和y=+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.6
【答案】C
【解析】因为与的图象都过点A(-2,0),
所以可得,,所以,
所以两函数表达式分别为.
因为直线与与y轴的交点分别为B(0,3),C(0,),
所以,故选C
【难度】一般
8.一次函数的大致图象是( )
【答案】A
【解析】
试题分析:主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.本题中因为a的取值不明确,故应分两种情况讨论,找出符合任一条件的选项即可.当a>0时,直线经过一,三,四象限,选项A正确;当a<0时,直线经过一,二,四象限,A、B、C、D均不符合此条件.故选A.
【难度】一般
9.关于直线y=-2x,下列结论正确的是( )
A.图象必过点(1,2)
B.图象经过第一、三象限
C.y随x的增大而减小
D.y随x的增大而增大
【答案】C
【解析】
试题分析:凡是函数图象经过的点必能满足解析式,进而得到A的正误,根据正比例函数性质可判定B、D的正误;根据两函数图象平行则k值相等可判断出C的正误,进而可得答案.
A.∵(1,2)不能使y=-2x左右相等,因此图象不经过(1,2)点,故此选项错误;
B.∵k=-2<0,∴图象经过第二、四象限,故此选项错误;
C.∵k=-2<0,∴y随x的增大而减小,故此选项正确;
D.∵k=-2<0,∴y随x的增大而减小,故此选项错误;
故选:C.
【难度】一般
10.如图,过点Q(0,3.5)的一次函数的图象与正比例函数的图象相交于点P,能表示这个一次函数图象的方程是( )
A. B.
C. D.
【答案】D
【解析】
试题分析:设这个一次函数的解析式为.
∵这条直线经过点P(1,2)和点Q(0,3.5),∴,解得,故这个一次函数的解析式为,即:.故选D.
【难度】一般
二、填空题(每小题2分,共20分)
11.写出一个实数k的值,使得正比例函数y=的图象在二、四象限 .
【答案】-1(答案不唯一)
【解析】
试题分析:当k<0时,正比例函数经过二、四象限;当k>0时,正比例函数经过一、三象限.(答案不唯一)
【难度】容易
12.某市地面气温是10,如果每升高1km,气温下降3,则气温y()与高度h(km)之间的函数关系式为________.
【答案】y=10-3h
【解析】
试题分析:气温=地面温度-降低的温度,把相关数值代入即可求解.解:高度为h,那么温度将降低3h,∴y=10-3h.
【难度】较易
13.如图,两直线交点B的坐标可以看作二元一次方程组 的解.
【答案】
【解析】因为函数图象交点坐标为两函数解析式组成的方程组的解.因此本题应该先用待定系数法求出两条直线的解析式,联立两直线解析式所组成的方程组即为所求的方程组.
解;设另一函数解析式为:y=kx+b,
∵图象经过(0,3)(1,2),
∴,
解得:,
∴函数解析式为:y=﹣x+3,
∴两直线交点B的坐标可以看作二元一次方程组的解,
故答案为:.
【难度】一般
14.已知一次函数y=kx+b的图象如图所示,当x<﹣1时,y的取值范围是 .
【答案】y<﹣6
【解析】根据一次函数过(2,0),(0,﹣4)求出k的值,得到一次函数解析式,然后用y表示x,再解关于x的不等式即可.
解:一次函数y=kx+b的图象与y轴交于点(0,﹣4),
∴b=﹣4,与x轴点(2,0),
∴0=2k﹣4,
∴k=2,
∴y=kx+b=2x﹣4,
∴x=(y+4)÷2<﹣1,
∴y<﹣6.
故答案为:y<﹣6.
【难度】一般
15.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶 千米.
【答案】
【解析】∵据函数图形知:甲用了30分钟行驶了12千米,乙用(18-6)分钟行驶了12千米,
∴甲每分钟行驶12÷30=千米,
乙每分钟行驶12÷12=1千米,
∴每分钟乙比甲多行驶1-=千米.
【难度】一般
16.已知一次函数与两个坐标轴围成的三角形面积为4,则________.
【答案】
【解析】直线与轴的交点坐标是,与轴的交点坐标是(0,),
根据三角形的面积是,得到,即,解得.
【难度】一般
17.点P(3,)、Q(,)在一次函数的图象上,则的大小关系是 .
【答案】a【解析】
试题分析:根据一次函数的性质可知,随着x值的增大,y值在减小,因为3>,所以a【难度】一般
18.下表给出的是关于某个一次函数的自变量x及其对应的函数值y的若干信息.请你根据表格中的相关数据计算:m+2n= .
【答案】6
【解析】
试题分析:本题考查待定系数法求函数解析式的知识,比较简单,注意掌握待定系数法的运用.设y=kx+b,将(-1,m)、(1,2)、(2,n)代入即可得出答案.
解:设一次函数解析式为:y=kx+b,则可得:-k+b=m①;k+b=2②;2k+b=n③;m+2n=①+2×③=3k+3b=3×2=6.故答案为:6.
【难度】一般
19.如图,直线y=﹣x+b与直线y=2x﹣3相交于点P(m,1),则不等式﹣x+b>2x﹣3的解集为________.
【答案】x<2
【解析】首先根据直线y=2x﹣3经过点P确定m=2,然后根据图象可知两直线交点P的坐标,根据图象可以看出当x<2时,一次函数y=2x﹣3的图象在y=﹣x+b的下方,即可得出答案.
解:∵点P(m,1)在直线y=2x﹣3上,
∴1=2x﹣3
∴m=2
当x<2时,一次函数y=2x﹣3的图象在y=﹣x+b的下方,
即﹣x+b>2x﹣3的解集为:x<2,
故答案为:x<2.
【难度】一般
20.已知关于x的函数同时满足下列三个条件:
①函数的图象不经过第二象限;
②当时,对应的函数值;
③当时,函数值y随x的增大而增大.
你认为符合要求的函数的解析式可以是:________(写出一个即可).
【答案】y=x-2
【解析】
试题分析:根据题目提供的条件①可以大体上确定函数图象的位置,再根据另外两个条件确定函数的解析式即可.
解:设函数的解析式为y=kx+b,
∵函数的图象不经过第二象限,∴b<0,
∵当x<2时,对应的函数值y<0,
∴其解析式可以为y=kx-2,
∵当x<2时,函数值y随x的增大而增大,∴k>0,
所以其解析式可以为y=x-2等,答案不唯一.
故答案为:y=x-2(答案不唯一)
【难度】较难
三、解答题(每小题10分,共70分)
21.已知一次函数y=kx+3的图象经过点(1,4)求这个一次函数的解析式,并求关于x的不等式kx+3≤6的解集.
【答案】y=x+3;x≤3
【解析】
试题分析:将点(1,4)代入函数解析式求出k的值,得出函数解析式;根据不等式的性质求出不等式的解.
试题解析:将点(1,4)代入得:k+3=4 解得:k=1
∴一次函数的解析式为y=x+3
根据k的值可得:不等式为x+3≤6 解得:x≤3.
【难度】较易
22.已知一次函数y=mx+m-2与y=2x-3的图象的交点A在y轴上,它们与x轴的交点分别为点B,点C.
(1)求m的值及△ABC的面积;
(2)求一次函数y=mx+m-2的图象上到x轴的距离等于2的点的坐标.
【答案】
(1)m=-1;;
(2)(-5,2)、(-1,-2).
【解析】
分析:(1)先根据坐标轴上点的坐标特征求出直线y=2x-3与坐标的两交点A(0,-3),C(,0),再把A(0,-3)代入y=mx+m-2得m=-1,然后确定B点坐标;利用三角形面积公式求△ABC的面积;
(2)把纵坐标为2或-2代入y=-x-1分别求出对应的横坐标即可.
解:(1)把x=0代入y=2x-3得y=-3,
所以A点坐标为(0,-3),
把y=0代入y=2x-3得2x-3=0,解得x=,
所以C点坐标为(,0),
把A(0,-3)代入y=mx+m-2得m-2=-3,
解得m=-1;
所以直线AB的解析式为y=-x-3,
把y=0代入y=-x-3得-x-3=0,解得x=-3,
所以B点坐标为(-3,0),
所以△ABC的面积=×3×(+3)=;
(2)把y=2代入y=-x-3得-x-3=2,解得x=-5;
把y=-2代入y=-x-3得-x-3=-2,解得x=-1,
所以一次函数y=mx+m-2的图象上到x轴的距离等于2的点的坐标为(-5,2)、(-1,-2).
【难度】一般
23.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组,请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
【答案】b=4;
(2)方程组的解为;
(3)直线l3经过点P,理由如下:
把P(1,4)代入直线l2:y=mx+n得m+n=4,
当x=1时,y=nx+m=m+n=4,
所以直线l3经过点P.
【解析】(1)直接把P点坐标代入y=3x+1即求出b的值;
(2)根据两直线相交的问题求解;
(3)先把P(1,4)代入y=mx+n得m+n=4,而当x=1时,y=nx+m=m+n=4,根据一次函数图象上点的坐标特征即可判断直线l3经过点P.
解:(1)把P(1,b)代入y=3x+1得b=3+1=4;
(2)方程组的解为;
(3)直线l3经过点P,理由如下:
把P(1,4)代入直线l2:y=mx+n得m+n=4,
当x=1时,y=nx+m=m+n=4,
所以直线l3经过点P.
【难度】一般
24.小丽一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干h后,途中在加油站加油若干L.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.
【答案】(1)行驶3h后加油,中途加油24L;
(2)Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
【解析】
试题分析:(1)观察图中数据可知,行驶3小时后油箱剩油6L,加油加至30L;
(2)先根据图中数据把每小时用油量求出来,即:(36-6)÷3=10L,再写出函数关系式;
(3)先要求出从加油站到景点需行几小时,然后再求需用多少油,便知是否够用.
试题解析:(1)从图中可知汽车行驶3h后加油,中途加油24L;
(2)根据分析可知Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
∵200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴油箱中的油是够用的.
【难度】一般
25.某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
A地 B地 C地
运费(元/件) 20 10 15
(1)设运往A地的水仙花x(件),总运费为y(元),试写出y与x的函数关系式;
(2)若总运费不超过12000元,最多可运往A地的水仙花多少件?
【答案】(1)y=25x+8000;(2)160件
【解析】(1)根据总运费=运往A地的费用+运往B地的费用+运往C地的费用,由条件就可以列出解析式;
(2)根据(1)的解析式建立不等式就可以求出结论.
解:(1)由运往A地的水仙花x(件),则运往C地3x件,运往B地(800-4x)件,由题意得
y=20x+10(800-4x)+45x,
y=25x+8000
(2)∵y≤12000,
∴25x+8000≤12000,
解得:x≤160
∴总运费不超过12000元,最多可运往A地的水仙花160件.
【难度】一般
26.某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
甲(kg) 乙(kg) 件数(件)
A 5x x
B 4(40-x) 40-x
(2)安排生产A、B两种产品的件数有几种方案?试说明理由;
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
【答案】(1)
甲(kg) 乙(kg) 件数(件)
A 8x 5x x
B 4(40-x) 9(40-x) 40-x
(2)共有三种方案:
方案一:A产品23件,B产品17件,
方案二:A产品24件,B产品16件,
方案三:A产品25件,B产品15件;
(3)y=-200x+44000 39400元
【解析】(1)根据总件数=单件需要的原料×件数列式即可;
(2)根据两种产品所需要的甲、乙两种原料列出不等式组,然后求解即可;
(3)根据总利润等于两种产品的利润之和列式整理,然后根据一次函数的增减性求出最大利润即可.
解:(1)表格分别填入:A甲种原料8x,B乙种原料9(40-x);
(2)根据题意得,
由①得,x≤25,
由②得,x≥22.5,
∴不等式组的解集是22.5≤x≤25,
∵x是正整数,
∴x=23、24、25,
共有三种方案:
方案一:A产品23件,B产品17件,
方案二:A产品24件,B产品16件,
方案三:A产品25件,B产品15件;
(3)y=900x+1100(40-x)=-200x+44000,
∵-200<0,
∴y随x的增大而减小,
∴x=23时,y有最大值,
y最大=-200×23+44000=39400元.
【难度】一般
27.如图,在平面直角坐标系中,点A,B在第一象限,AB∥x轴,AB=2,点Q(6,0),根据图象回答:
(1)点B的坐标是 ;
(2)分别求出OA,BC所在直线的解析式;
(3)P是一动点,在折线OABC上沿O→A→B→C运动,不与O、C重合,点P(x,y),△OPQ的面积为S,求S与x的函数关系式,并指出自变量x的取值范围;
(4)在给出的坐标系中画出S随x变化的函数图象.
【答案】(1)(4,4),
(2)直线OA的解析式为y=2x;
直线BC的解析式是y=﹣x+8;
(3)分三种情况:
①当点P在OA上运动时,如图1,则PE=y=2x,
S=(0<x≤2)
②当点P在AB上运动时,如图2,则PE=4,
S=(2≤x≤4)
③当点P在BC上运动时,如图3,则PE=y=﹣x+8,
S=(4≤x<8);
(4)如图:
【解析】(1)根据图象即可得出B的坐标;
(2)设OA的解析式为y=kx,把A(2,4)代入求出k即可;设BC的解析式为y=mx+b,把B(4,4),C(8,0)代入得出方程组,求出m b即可;
(3)过P作PE⊥OC于E,分三种情况:①当点P在OA上运动时,则PE=y=2x,②当点P在AB上运动时,则PE=4③当点P在BC上运动时,则PE=y=﹣x+8,根据三角形的面积公式求出即可;
(4)根据三个函数式在平面直角坐标系中画出即可.
解:(1)点B的坐标是(4,4),
故答案为:(4,4);
(2)设OA的解析式为y=kx,
把A(2,4)代入得:2k=4,
解得:k=2
∴直线OA的解析式为y=2x;
设BC的解析式为y=mx+b,
把B(4,4),C(8,0)代入得:,
解得:m=﹣1,b=8,
直线BC的解析式是y=﹣x+8;
(3)过P作PE⊥OC于E,
∵点Q(6,0),
∴OQ=6,
分三种情况:
①当点P在OA上运动时,如图1,则PE=y=2x,
S=(0<x≤2)
②当点P在AB上运动时,如图2,则PE=4,
S=(2≤x≤4)
③当点P在BC上运动时,如图3,则PE=y=﹣x+8,
S=(4≤x<8);
(4)如图:
【难度】困难
一、选择题(每小题3分,共30分)
1.若函数是一次函数,则应满足的条件是( )
A.且 B.且
C.且 D.且
2.直线y=2x经过平移可以得到直线y=2x-2的是
A.向左平移2个单位 B.向右平移2个单位
C.向下平移2个单位 D.向上平移 2个单位
3.已知正比例函数y=kx(k≠0)的图象经过点(1,-2),则这个正比例函数的解析式为( )
A.y=2x B.y= 2x C.y=x D.y= x
4.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )
A.
B.
C.
D.
5.两直线l1:y=2x-1,l2:y=x+1的交点坐标为( )
A.(-2,3) B.(2,-3)
C.(-2,-3) D.(2,3)
6.一次函数y=-2x+4的图象与y轴的交点坐标是( )
A.(0,4) B.(4,0)
C.(2,0) D.(0,2)
7.已知一次函数y=+m和y=+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.6
8.一次函数的大致图象是( )
9.关于直线y=-2x,下列结论正确的是( )
A.图象必过点(1,2)
B.图象经过第一、三象限
C.y随x的增大而减小
D.y随x的增大而增大
10.如图,过点Q(0,3.5)的一次函数的图象与正比例函数的图象相交于点P,能表示这个一次函数图象的方程是( )
A. B.
C. D.
二、填空题(每小题2分,共20分)
11.写出一个实数k的值,使得正比例函数y=的图象在二、四象限 .
12.某市地面气温是10,如果每升高1km,气温下降3,则气温y()与高度h(km)之间的函数关系式为________.
13.如图,两直线交点B的坐标可以看作二元一次方程组 的解.
14.已知一次函数y=kx+b的图象如图所示,当x<﹣1时,y的取值范围是 .
15.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶 千米.
16.已知一次函数与两个坐标轴围成的三角形面积为4,则________.
17.点P(3,)、Q(,)在一次函数的图象上,则的大小关系是 .
18.下表给出的是关于某个一次函数的自变量x及其对应的函数值y的若干信息.请你根据表格中的相关数据计算:m+2n= .
19.如图,直线y=﹣x+b与直线y=2x﹣3相交于点P(m,1),则不等式﹣x+b>2x﹣3的解集为________.
20.已知关于x的函数同时满足下列三个条件:
①函数的图象不经过第二象限;
②当时,对应的函数值;
③当时,函数值y随x的增大而增大.
你认为符合要求的函数的解析式可以是:________(写出一个即可).
三、解答题(每小题10分,共70分)
21.已知一次函数y=kx+3的图象经过点(1,4)求这个一次函数的解析式,并求关于x的不等式kx+3≤6的解集.
22.已知一次函数y=mx+m-2与y=2x-3的图象的交点A在y轴上,它们与x轴的交点分别为点B,点C.
(1)求m的值及△ABC的面积;
(2)求一次函数y=mx+m-2的图象上到x轴的距离等于2的点的坐标.
23.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组,请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
24.小丽一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干h后,途中在加油站加油若干L.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.
25.某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
A地 B地 C地
运费(元/件) 20 10 15
(1)设运往A地的水仙花x(件),总运费为y(元),试写出y与x的函数关系式;
(2)若总运费不超过12000元,最多可运往A地的水仙花多少件?
26.某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
甲(kg) 乙(kg) 件数(件)
A 5x x
B 4(40-x) 40-x
(2)安排生产A、B两种产品的件数有几种方案?试说明理由;
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
27.如图,在平面直角坐标系中,点A,B在第一象限,AB∥x轴,AB=2,点Q(6,0),根据图象回答:
(1)点B的坐标是 ;
(2)分别求出OA,BC所在直线的解析式;
(3)P是一动点,在折线OABC上沿O→A→B→C运动,不与O、C重合,点P(x,y),△OPQ的面积为S,求S与x的函数关系式,并指出自变量x的取值范围;
(4)在给出的坐标系中画出S随x变化的函数图象.
答案解析
一、选择题(每小题3分,共30分)
1.若函数是一次函数,则应满足的条件是( )
A.且 B.且
C.且 D.且
【答案】C
【解析】∵ 函数是一次函数,∴ 解得故选C.
【难度】容易
2.直线y=2x经过平移可以得到直线y=2x-2的是
A.向左平移2个单位 B.向右平移2个单位
C.向下平移2个单位 D.向上平移 2个单位
【答案】C
【解析】
试题分析:根据上加下减的平移原则,直线y=2x-2可以看作是由直线y=2x向下平移2个单位得到的;
故选C.
【难度】较易
3.已知正比例函数y=kx(k≠0)的图象经过点(1,-2),则这个正比例函数的解析式为( )
A.y=2x B.y= 2x C.y=x D.y= x
【答案】B
【解析】利用待定系数法把(1,-2)代入正比例函数y=kx中计算出k即可得到解析式.
解:∵正比例函数y=kx经过点(1,-2),
∴-2=1 k,
解得:k=-2,
∴这个正比例函数的解析式为:y=-2x.
故选B.
【难度】较易
4.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )
A.
B.
C.
D.
【答案】C
【解析】分三段讨论,①两车从开始到相遇,这段时间两车距迅速减小,②相遇后向相反方向行驶至特快到达甲地,这段时间两车距迅速增加,③特快到达甲地至快车到达乙地,这段时间两车距缓慢增大,结合实际选符合的图象即可.
解:①两车从开始到相遇,这段时间两车距迅速减小;
②相遇后向相反方向行驶至特快到达甲地,这段时间两车距迅速增加;
③特快到达甲地至快车到达乙地,这段时间两车距缓慢增大;
结合图象可得C选项符合题意.
故选C.
【难度】一般
5.两直线l1:y=2x-1,l2:y=x+1的交点坐标为( )
A.(-2,3) B.(2,-3)
C.(-2,-3) D.(2,3)
【答案】D
【解析】∵方程组的解是
∴选D.
【难度】一般
6.一次函数y=-2x+4的图象与y轴的交点坐标是( )
A.(0,4) B.(4,0)
C.(2,0) D.(0,2)
【答案】A
【解析】 令x=0,得y=-2×0+4=4,
则函数图象与y轴的交点坐标是(0,4).
【难度】一般
7.已知一次函数y=+m和y=+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.6
【答案】C
【解析】因为与的图象都过点A(-2,0),
所以可得,,所以,
所以两函数表达式分别为.
因为直线与与y轴的交点分别为B(0,3),C(0,),
所以,故选C
【难度】一般
8.一次函数的大致图象是( )
【答案】A
【解析】
试题分析:主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.一次函数y=kx+b的图象有四种情况:①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.本题中因为a的取值不明确,故应分两种情况讨论,找出符合任一条件的选项即可.当a>0时,直线经过一,三,四象限,选项A正确;当a<0时,直线经过一,二,四象限,A、B、C、D均不符合此条件.故选A.
【难度】一般
9.关于直线y=-2x,下列结论正确的是( )
A.图象必过点(1,2)
B.图象经过第一、三象限
C.y随x的增大而减小
D.y随x的增大而增大
【答案】C
【解析】
试题分析:凡是函数图象经过的点必能满足解析式,进而得到A的正误,根据正比例函数性质可判定B、D的正误;根据两函数图象平行则k值相等可判断出C的正误,进而可得答案.
A.∵(1,2)不能使y=-2x左右相等,因此图象不经过(1,2)点,故此选项错误;
B.∵k=-2<0,∴图象经过第二、四象限,故此选项错误;
C.∵k=-2<0,∴y随x的增大而减小,故此选项正确;
D.∵k=-2<0,∴y随x的增大而减小,故此选项错误;
故选:C.
【难度】一般
10.如图,过点Q(0,3.5)的一次函数的图象与正比例函数的图象相交于点P,能表示这个一次函数图象的方程是( )
A. B.
C. D.
【答案】D
【解析】
试题分析:设这个一次函数的解析式为.
∵这条直线经过点P(1,2)和点Q(0,3.5),∴,解得,故这个一次函数的解析式为,即:.故选D.
【难度】一般
二、填空题(每小题2分,共20分)
11.写出一个实数k的值,使得正比例函数y=的图象在二、四象限 .
【答案】-1(答案不唯一)
【解析】
试题分析:当k<0时,正比例函数经过二、四象限;当k>0时,正比例函数经过一、三象限.(答案不唯一)
【难度】容易
12.某市地面气温是10,如果每升高1km,气温下降3,则气温y()与高度h(km)之间的函数关系式为________.
【答案】y=10-3h
【解析】
试题分析:气温=地面温度-降低的温度,把相关数值代入即可求解.解:高度为h,那么温度将降低3h,∴y=10-3h.
【难度】较易
13.如图,两直线交点B的坐标可以看作二元一次方程组 的解.
【答案】
【解析】因为函数图象交点坐标为两函数解析式组成的方程组的解.因此本题应该先用待定系数法求出两条直线的解析式,联立两直线解析式所组成的方程组即为所求的方程组.
解;设另一函数解析式为:y=kx+b,
∵图象经过(0,3)(1,2),
∴,
解得:,
∴函数解析式为:y=﹣x+3,
∴两直线交点B的坐标可以看作二元一次方程组的解,
故答案为:.
【难度】一般
14.已知一次函数y=kx+b的图象如图所示,当x<﹣1时,y的取值范围是 .
【答案】y<﹣6
【解析】根据一次函数过(2,0),(0,﹣4)求出k的值,得到一次函数解析式,然后用y表示x,再解关于x的不等式即可.
解:一次函数y=kx+b的图象与y轴交于点(0,﹣4),
∴b=﹣4,与x轴点(2,0),
∴0=2k﹣4,
∴k=2,
∴y=kx+b=2x﹣4,
∴x=(y+4)÷2<﹣1,
∴y<﹣6.
故答案为:y<﹣6.
【难度】一般
15.甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶 千米.
【答案】
【解析】∵据函数图形知:甲用了30分钟行驶了12千米,乙用(18-6)分钟行驶了12千米,
∴甲每分钟行驶12÷30=千米,
乙每分钟行驶12÷12=1千米,
∴每分钟乙比甲多行驶1-=千米.
【难度】一般
16.已知一次函数与两个坐标轴围成的三角形面积为4,则________.
【答案】
【解析】直线与轴的交点坐标是,与轴的交点坐标是(0,),
根据三角形的面积是,得到,即,解得.
【难度】一般
17.点P(3,)、Q(,)在一次函数的图象上,则的大小关系是 .
【答案】a
试题分析:根据一次函数的性质可知,随着x值的增大,y值在减小,因为3>,所以a
18.下表给出的是关于某个一次函数的自变量x及其对应的函数值y的若干信息.请你根据表格中的相关数据计算:m+2n= .
【答案】6
【解析】
试题分析:本题考查待定系数法求函数解析式的知识,比较简单,注意掌握待定系数法的运用.设y=kx+b,将(-1,m)、(1,2)、(2,n)代入即可得出答案.
解:设一次函数解析式为:y=kx+b,则可得:-k+b=m①;k+b=2②;2k+b=n③;m+2n=①+2×③=3k+3b=3×2=6.故答案为:6.
【难度】一般
19.如图,直线y=﹣x+b与直线y=2x﹣3相交于点P(m,1),则不等式﹣x+b>2x﹣3的解集为________.
【答案】x<2
【解析】首先根据直线y=2x﹣3经过点P确定m=2,然后根据图象可知两直线交点P的坐标,根据图象可以看出当x<2时,一次函数y=2x﹣3的图象在y=﹣x+b的下方,即可得出答案.
解:∵点P(m,1)在直线y=2x﹣3上,
∴1=2x﹣3
∴m=2
当x<2时,一次函数y=2x﹣3的图象在y=﹣x+b的下方,
即﹣x+b>2x﹣3的解集为:x<2,
故答案为:x<2.
【难度】一般
20.已知关于x的函数同时满足下列三个条件:
①函数的图象不经过第二象限;
②当时,对应的函数值;
③当时,函数值y随x的增大而增大.
你认为符合要求的函数的解析式可以是:________(写出一个即可).
【答案】y=x-2
【解析】
试题分析:根据题目提供的条件①可以大体上确定函数图象的位置,再根据另外两个条件确定函数的解析式即可.
解:设函数的解析式为y=kx+b,
∵函数的图象不经过第二象限,∴b<0,
∵当x<2时,对应的函数值y<0,
∴其解析式可以为y=kx-2,
∵当x<2时,函数值y随x的增大而增大,∴k>0,
所以其解析式可以为y=x-2等,答案不唯一.
故答案为:y=x-2(答案不唯一)
【难度】较难
三、解答题(每小题10分,共70分)
21.已知一次函数y=kx+3的图象经过点(1,4)求这个一次函数的解析式,并求关于x的不等式kx+3≤6的解集.
【答案】y=x+3;x≤3
【解析】
试题分析:将点(1,4)代入函数解析式求出k的值,得出函数解析式;根据不等式的性质求出不等式的解.
试题解析:将点(1,4)代入得:k+3=4 解得:k=1
∴一次函数的解析式为y=x+3
根据k的值可得:不等式为x+3≤6 解得:x≤3.
【难度】较易
22.已知一次函数y=mx+m-2与y=2x-3的图象的交点A在y轴上,它们与x轴的交点分别为点B,点C.
(1)求m的值及△ABC的面积;
(2)求一次函数y=mx+m-2的图象上到x轴的距离等于2的点的坐标.
【答案】
(1)m=-1;;
(2)(-5,2)、(-1,-2).
【解析】
分析:(1)先根据坐标轴上点的坐标特征求出直线y=2x-3与坐标的两交点A(0,-3),C(,0),再把A(0,-3)代入y=mx+m-2得m=-1,然后确定B点坐标;利用三角形面积公式求△ABC的面积;
(2)把纵坐标为2或-2代入y=-x-1分别求出对应的横坐标即可.
解:(1)把x=0代入y=2x-3得y=-3,
所以A点坐标为(0,-3),
把y=0代入y=2x-3得2x-3=0,解得x=,
所以C点坐标为(,0),
把A(0,-3)代入y=mx+m-2得m-2=-3,
解得m=-1;
所以直线AB的解析式为y=-x-3,
把y=0代入y=-x-3得-x-3=0,解得x=-3,
所以B点坐标为(-3,0),
所以△ABC的面积=×3×(+3)=;
(2)把y=2代入y=-x-3得-x-3=2,解得x=-5;
把y=-2代入y=-x-3得-x-3=-2,解得x=-1,
所以一次函数y=mx+m-2的图象上到x轴的距离等于2的点的坐标为(-5,2)、(-1,-2).
【难度】一般
23.如图,直线l1:y=3x+1与直线l2:y=mx+n相交于点P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组,请你直接写出它的解;
(3)直线l3:y=nx+m是否也经过点P?请说明理由.
【答案】b=4;
(2)方程组的解为;
(3)直线l3经过点P,理由如下:
把P(1,4)代入直线l2:y=mx+n得m+n=4,
当x=1时,y=nx+m=m+n=4,
所以直线l3经过点P.
【解析】(1)直接把P点坐标代入y=3x+1即求出b的值;
(2)根据两直线相交的问题求解;
(3)先把P(1,4)代入y=mx+n得m+n=4,而当x=1时,y=nx+m=m+n=4,根据一次函数图象上点的坐标特征即可判断直线l3经过点P.
解:(1)把P(1,b)代入y=3x+1得b=3+1=4;
(2)方程组的解为;
(3)直线l3经过点P,理由如下:
把P(1,4)代入直线l2:y=mx+n得m+n=4,
当x=1时,y=nx+m=m+n=4,
所以直线l3经过点P.
【难度】一般
24.小丽一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干h后,途中在加油站加油若干L.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
(1)小汽车行驶________h后加油, 中途加油__________L;
(2)求加油前油箱余油量Q与行驶时间t的函数关系式;
(3)如果加油站距景点200km,车速为80km/h,要到达目的地,油箱中的油是否够用?请说明理由.
【答案】(1)行驶3h后加油,中途加油24L;
(2)Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
【解析】
试题分析:(1)观察图中数据可知,行驶3小时后油箱剩油6L,加油加至30L;
(2)先根据图中数据把每小时用油量求出来,即:(36-6)÷3=10L,再写出函数关系式;
(3)先要求出从加油站到景点需行几小时,然后再求需用多少油,便知是否够用.
试题解析:(1)从图中可知汽车行驶3h后加油,中途加油24L;
(2)根据分析可知Q=-10t+36(0≤t≤3);
(3)油箱中的油是够用的.
∵200÷80=2.5(小时),需用油10×2.5=25L<30L,
∴油箱中的油是够用的.
【难度】一般
25.某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
A地 B地 C地
运费(元/件) 20 10 15
(1)设运往A地的水仙花x(件),总运费为y(元),试写出y与x的函数关系式;
(2)若总运费不超过12000元,最多可运往A地的水仙花多少件?
【答案】(1)y=25x+8000;(2)160件
【解析】(1)根据总运费=运往A地的费用+运往B地的费用+运往C地的费用,由条件就可以列出解析式;
(2)根据(1)的解析式建立不等式就可以求出结论.
解:(1)由运往A地的水仙花x(件),则运往C地3x件,运往B地(800-4x)件,由题意得
y=20x+10(800-4x)+45x,
y=25x+8000
(2)∵y≤12000,
∴25x+8000≤12000,
解得:x≤160
∴总运费不超过12000元,最多可运往A地的水仙花160件.
【难度】一般
26.某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
甲(kg) 乙(kg) 件数(件)
A 5x x
B 4(40-x) 40-x
(2)安排生产A、B两种产品的件数有几种方案?试说明理由;
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
【答案】(1)
甲(kg) 乙(kg) 件数(件)
A 8x 5x x
B 4(40-x) 9(40-x) 40-x
(2)共有三种方案:
方案一:A产品23件,B产品17件,
方案二:A产品24件,B产品16件,
方案三:A产品25件,B产品15件;
(3)y=-200x+44000 39400元
【解析】(1)根据总件数=单件需要的原料×件数列式即可;
(2)根据两种产品所需要的甲、乙两种原料列出不等式组,然后求解即可;
(3)根据总利润等于两种产品的利润之和列式整理,然后根据一次函数的增减性求出最大利润即可.
解:(1)表格分别填入:A甲种原料8x,B乙种原料9(40-x);
(2)根据题意得,
由①得,x≤25,
由②得,x≥22.5,
∴不等式组的解集是22.5≤x≤25,
∵x是正整数,
∴x=23、24、25,
共有三种方案:
方案一:A产品23件,B产品17件,
方案二:A产品24件,B产品16件,
方案三:A产品25件,B产品15件;
(3)y=900x+1100(40-x)=-200x+44000,
∵-200<0,
∴y随x的增大而减小,
∴x=23时,y有最大值,
y最大=-200×23+44000=39400元.
【难度】一般
27.如图,在平面直角坐标系中,点A,B在第一象限,AB∥x轴,AB=2,点Q(6,0),根据图象回答:
(1)点B的坐标是 ;
(2)分别求出OA,BC所在直线的解析式;
(3)P是一动点,在折线OABC上沿O→A→B→C运动,不与O、C重合,点P(x,y),△OPQ的面积为S,求S与x的函数关系式,并指出自变量x的取值范围;
(4)在给出的坐标系中画出S随x变化的函数图象.
【答案】(1)(4,4),
(2)直线OA的解析式为y=2x;
直线BC的解析式是y=﹣x+8;
(3)分三种情况:
①当点P在OA上运动时,如图1,则PE=y=2x,
S=(0<x≤2)
②当点P在AB上运动时,如图2,则PE=4,
S=(2≤x≤4)
③当点P在BC上运动时,如图3,则PE=y=﹣x+8,
S=(4≤x<8);
(4)如图:
【解析】(1)根据图象即可得出B的坐标;
(2)设OA的解析式为y=kx,把A(2,4)代入求出k即可;设BC的解析式为y=mx+b,把B(4,4),C(8,0)代入得出方程组,求出m b即可;
(3)过P作PE⊥OC于E,分三种情况:①当点P在OA上运动时,则PE=y=2x,②当点P在AB上运动时,则PE=4③当点P在BC上运动时,则PE=y=﹣x+8,根据三角形的面积公式求出即可;
(4)根据三个函数式在平面直角坐标系中画出即可.
解:(1)点B的坐标是(4,4),
故答案为:(4,4);
(2)设OA的解析式为y=kx,
把A(2,4)代入得:2k=4,
解得:k=2
∴直线OA的解析式为y=2x;
设BC的解析式为y=mx+b,
把B(4,4),C(8,0)代入得:,
解得:m=﹣1,b=8,
直线BC的解析式是y=﹣x+8;
(3)过P作PE⊥OC于E,
∵点Q(6,0),
∴OQ=6,
分三种情况:
①当点P在OA上运动时,如图1,则PE=y=2x,
S=(0<x≤2)
②当点P在AB上运动时,如图2,则PE=4,
S=(2≤x≤4)
③当点P在BC上运动时,如图3,则PE=y=﹣x+8,
S=(4≤x<8);
(4)如图:
【难度】困难
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
