4.5 增长速度的比较 教案
文档属性
| 名称 | 4.5 增长速度的比较 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 182.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 17:56:17 | ||
图片预览


文档简介
4.5 增长速度的比较 教案
教学课时:第1课时
教学目标:
1、通过实例理解如何用函数的平均变化率比较函数值变化的快慢,了解函数平均变化率与连接区间端点的直线的斜率的关系;
2、会简单比较指数增长、线性增长、对数增长的增长速度大小;
3、了解指数增长、线性增长、对数增长等数学模型在生活中的应用,提升数学运算和数学建模等核心素养。
教学重点:
用平均变化率理解函数的增长速度。
教学难点:
比较指数增长、线性增长、对数增长的增长速度。
教学过程:
一、情境与问题
有一套房子,价格为200万元,假设房价每年上涨10%,某人每年固定能攒下40万元,如果他想买这套房子,在不贷款、收入不增加的前提下,这个人需要多少年才能攒够钱买这套房子?
A.5年 B.7年 C.8年 D.9年 E.永远也买不起
问题1:凭直觉,你认为上述问题的答案是什么?为什么?
预设答案:选E,因为房价的增长速度比攒钱的增长速度快。
问题2:房价的增长速度一直都比攒钱的增长速度快吗?怎么刻画它们的增长速度呢?
预设答案:不一定,经过1年,房价增长了20万元,攒钱增长了40万元,这个房价的增长速度就没有攒钱的增长速度快.我们可以用函数的平均变化率来刻画,也就是看相同时间内这两个函数值的增加量的大小。
师:我们先研究几个基本初等函数的变化情况。
【设计意图】
从实际问题和生活经验感受房价的增长速度与攒钱的速度的快慢,引入刻画函数变化快慢的量——函数的平均变化率,后面再从数学角度建立函数模型,将问题转化为研究两个函数的增长速度,回扣情境,解决问题。
二、基本初等函数的增长速度
问题3:一般地,函数f(x)在区间上的平均变化率怎么表示?
预设答案:
老师:为了简便计算,我们常常可以令
例1. 已知函数,分别计算这三个函数在区间上的平均变化率。
解:
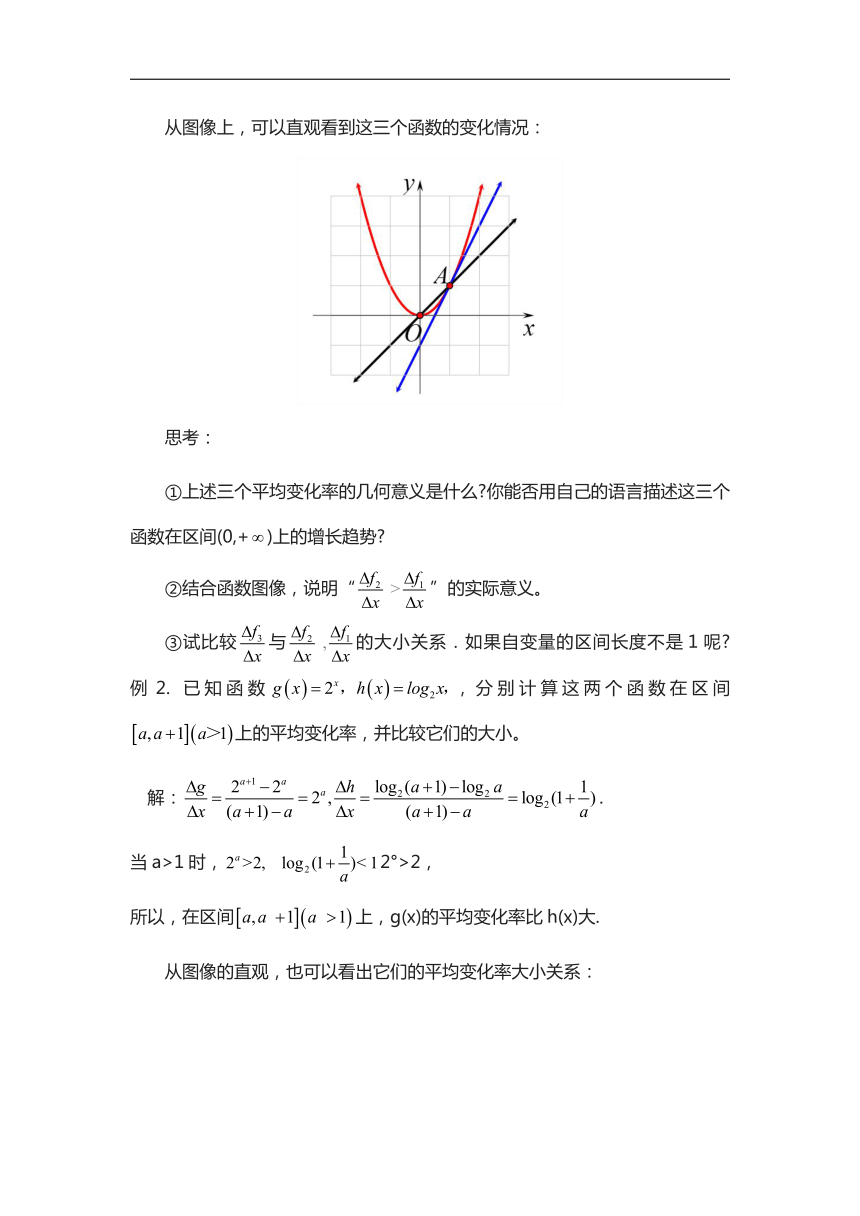
从图像上,可以直观看到这三个函数的变化情况:
思考:
①上述三个平均变化率的几何意义是什么 你能否用自己的语言描述这三个函数在区间(0,+)上的增长趋势
②结合函数图像,说明“”的实际意义。
③试比较与的大小关系.如果自变量的区间长度不是1呢 例2. 已知函数,分别计算这两个函数在区间上的平均变化率,并比较它们的大小。
解:.
当a>1时,2°>2,
所以,在区间上,g(x)的平均变化率比h(x)大.
从图像的直观,也可以看出它们的平均变化率大小关系:
思考:
①当0<a<1时,g(x)的平均变化率还一定比h(x)大吗?
②比较g(x)和h(x)与例1中三个函数的平均变化率的变化趋势,你能得到什么结论?
③能否举一些生活中指数增长、线性增长、对数增长的例子?
【设计意图】
从基本初等函数的平均变化率理解函数的增长速度,有利于本节课教学目标的达成,结合函数图象,有利于学生对几种不同类型函数的增长速度有一个直观的比较.同时,在具体推理演算过程中,培养学生的数学运算能力。
三、回扣情境与问题
问题4:我们再来研究本节课开始的问题:
设经过x(xN)年后,房价为h(x)万元,这个人攒下的钱共有r(x)万元,则这两个函数的解析式分别为: h(x)=200×1.1*,r(x)=40x,xN,在区间[a,a+1](aN)上,
令
即a≥8时,房价的增长速度比攒钱的增长速度快.﹒
我们也可以列表,直观地看一看这两个函数值(取整数,单位:万元)的变化情况:
x的值每增加1,r(x)的值稳定地增长40,而h(x)的值的增加量则逐渐变大,并且越来越快。经过8年后,h(x)的值的年增加量将接近40,以后则均大于40。在前8年里,攒钱的总数始终小于房价,所以,这个人永远也买不起房子。
当然,这只是一个理想化的数学问题.现实生活中,“房住不炒”,房价不可能呈现指数增长的态势增长,甚至还可能会出现环比下跌,况且人们还可以按揭贷款买房。
【设计意图】
回扣情境,建立数学模型,解决实际问题,让整节课从问题开始,又回到问题解决中去,在整个环节中,认识几种基本初等函数的增长速度的快慢,初步理解指数增长、线性增长的实际意义。
四、课堂练习
1.(课本第41页习题4-5A第1题)
求f(x)=5x+1在任意区间上的平均变化率,并说明自变量每增加1个单位时函数值的变化情况。
参考答案:平均变化率为5,自变量每增加1个单位时,函数值将增加5个单位.
2.(课本第41页习题4-5B第1题)
已知函数f(x)的定义域为R,分别判断下列条件下f(x)的单调性:
(1)f(x)在任意区间内的平均变化率均为正数;
(2)f(x)在任意区间内的平均变化率均比g(x)=2在同一区间内的平均变化率小。
参考答案:(1)单调递增;(2)单调递减。
3.(课本第41页习题4-5B第3题)
已知函数f(x)在任意区间内的平均变化率均为5,说明当自变量减小3个单位时,函数值的变化情况。
参考答案:函数值将减小15个单位。
五、课堂小结
1. 函数的平均变化率刻画函数的增长速度的快慢;
2. 简单比较指数增长、线性增长、对数增长的增长速度。
六、布置作业
1. 阅读课本第40页拓展阅读“指数运算与生活哲学”,并举出一个生活中的指数增长的例子;
2. 课本第41页习题4-5A第2、3题;B第2、4题。
3. 学有余力的同学思考:课本第41页习题4-5C第1、2题。
教学课时:第1课时
教学目标:
1、通过实例理解如何用函数的平均变化率比较函数值变化的快慢,了解函数平均变化率与连接区间端点的直线的斜率的关系;
2、会简单比较指数增长、线性增长、对数增长的增长速度大小;
3、了解指数增长、线性增长、对数增长等数学模型在生活中的应用,提升数学运算和数学建模等核心素养。
教学重点:
用平均变化率理解函数的增长速度。
教学难点:
比较指数增长、线性增长、对数增长的增长速度。
教学过程:
一、情境与问题
有一套房子,价格为200万元,假设房价每年上涨10%,某人每年固定能攒下40万元,如果他想买这套房子,在不贷款、收入不增加的前提下,这个人需要多少年才能攒够钱买这套房子?
A.5年 B.7年 C.8年 D.9年 E.永远也买不起
问题1:凭直觉,你认为上述问题的答案是什么?为什么?
预设答案:选E,因为房价的增长速度比攒钱的增长速度快。
问题2:房价的增长速度一直都比攒钱的增长速度快吗?怎么刻画它们的增长速度呢?
预设答案:不一定,经过1年,房价增长了20万元,攒钱增长了40万元,这个房价的增长速度就没有攒钱的增长速度快.我们可以用函数的平均变化率来刻画,也就是看相同时间内这两个函数值的增加量的大小。
师:我们先研究几个基本初等函数的变化情况。
【设计意图】
从实际问题和生活经验感受房价的增长速度与攒钱的速度的快慢,引入刻画函数变化快慢的量——函数的平均变化率,后面再从数学角度建立函数模型,将问题转化为研究两个函数的增长速度,回扣情境,解决问题。
二、基本初等函数的增长速度
问题3:一般地,函数f(x)在区间上的平均变化率怎么表示?
预设答案:
老师:为了简便计算,我们常常可以令
例1. 已知函数,分别计算这三个函数在区间上的平均变化率。
解:
从图像上,可以直观看到这三个函数的变化情况:
思考:
①上述三个平均变化率的几何意义是什么 你能否用自己的语言描述这三个函数在区间(0,+)上的增长趋势
②结合函数图像,说明“”的实际意义。
③试比较与的大小关系.如果自变量的区间长度不是1呢 例2. 已知函数,分别计算这两个函数在区间上的平均变化率,并比较它们的大小。
解:.
当a>1时,2°>2,
所以,在区间上,g(x)的平均变化率比h(x)大.
从图像的直观,也可以看出它们的平均变化率大小关系:
思考:
①当0<a<1时,g(x)的平均变化率还一定比h(x)大吗?
②比较g(x)和h(x)与例1中三个函数的平均变化率的变化趋势,你能得到什么结论?
③能否举一些生活中指数增长、线性增长、对数增长的例子?
【设计意图】
从基本初等函数的平均变化率理解函数的增长速度,有利于本节课教学目标的达成,结合函数图象,有利于学生对几种不同类型函数的增长速度有一个直观的比较.同时,在具体推理演算过程中,培养学生的数学运算能力。
三、回扣情境与问题
问题4:我们再来研究本节课开始的问题:
设经过x(xN)年后,房价为h(x)万元,这个人攒下的钱共有r(x)万元,则这两个函数的解析式分别为: h(x)=200×1.1*,r(x)=40x,xN,在区间[a,a+1](aN)上,
令
即a≥8时,房价的增长速度比攒钱的增长速度快.﹒
我们也可以列表,直观地看一看这两个函数值(取整数,单位:万元)的变化情况:
x的值每增加1,r(x)的值稳定地增长40,而h(x)的值的增加量则逐渐变大,并且越来越快。经过8年后,h(x)的值的年增加量将接近40,以后则均大于40。在前8年里,攒钱的总数始终小于房价,所以,这个人永远也买不起房子。
当然,这只是一个理想化的数学问题.现实生活中,“房住不炒”,房价不可能呈现指数增长的态势增长,甚至还可能会出现环比下跌,况且人们还可以按揭贷款买房。
【设计意图】
回扣情境,建立数学模型,解决实际问题,让整节课从问题开始,又回到问题解决中去,在整个环节中,认识几种基本初等函数的增长速度的快慢,初步理解指数增长、线性增长的实际意义。
四、课堂练习
1.(课本第41页习题4-5A第1题)
求f(x)=5x+1在任意区间上的平均变化率,并说明自变量每增加1个单位时函数值的变化情况。
参考答案:平均变化率为5,自变量每增加1个单位时,函数值将增加5个单位.
2.(课本第41页习题4-5B第1题)
已知函数f(x)的定义域为R,分别判断下列条件下f(x)的单调性:
(1)f(x)在任意区间内的平均变化率均为正数;
(2)f(x)在任意区间内的平均变化率均比g(x)=2在同一区间内的平均变化率小。
参考答案:(1)单调递增;(2)单调递减。
3.(课本第41页习题4-5B第3题)
已知函数f(x)在任意区间内的平均变化率均为5,说明当自变量减小3个单位时,函数值的变化情况。
参考答案:函数值将减小15个单位。
五、课堂小结
1. 函数的平均变化率刻画函数的增长速度的快慢;
2. 简单比较指数增长、线性增长、对数增长的增长速度。
六、布置作业
1. 阅读课本第40页拓展阅读“指数运算与生活哲学”,并举出一个生活中的指数增长的例子;
2. 课本第41页习题4-5A第2、3题;B第2、4题。
3. 学有余力的同学思考:课本第41页习题4-5C第1、2题。
