人教版八年级数学上册12.2三角形全等的判定(1-4)提升练习 (含答案)
文档属性
| 名称 | 人教版八年级数学上册12.2三角形全等的判定(1-4)提升练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 295.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 09:07:47 | ||
图片预览


文档简介
浙教版-8年级-上册-数学-第1章《三角形的初步知识》
1.5三角形全等的判定
【知识点-部分】
一、全等三角形判定1——“边边边”
1、三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
二、全等三角形判定2——“边角边”
1、两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
2、有两边和其中一边的对角对应相等,两个三角形不一定全等.
三、全等三角形判定3——“角边角”
1、两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
四、全等三角形判定4——“角角边”
1、两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
2、由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论。
【典型例题-精选部分】
1、在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.
(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.
(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.
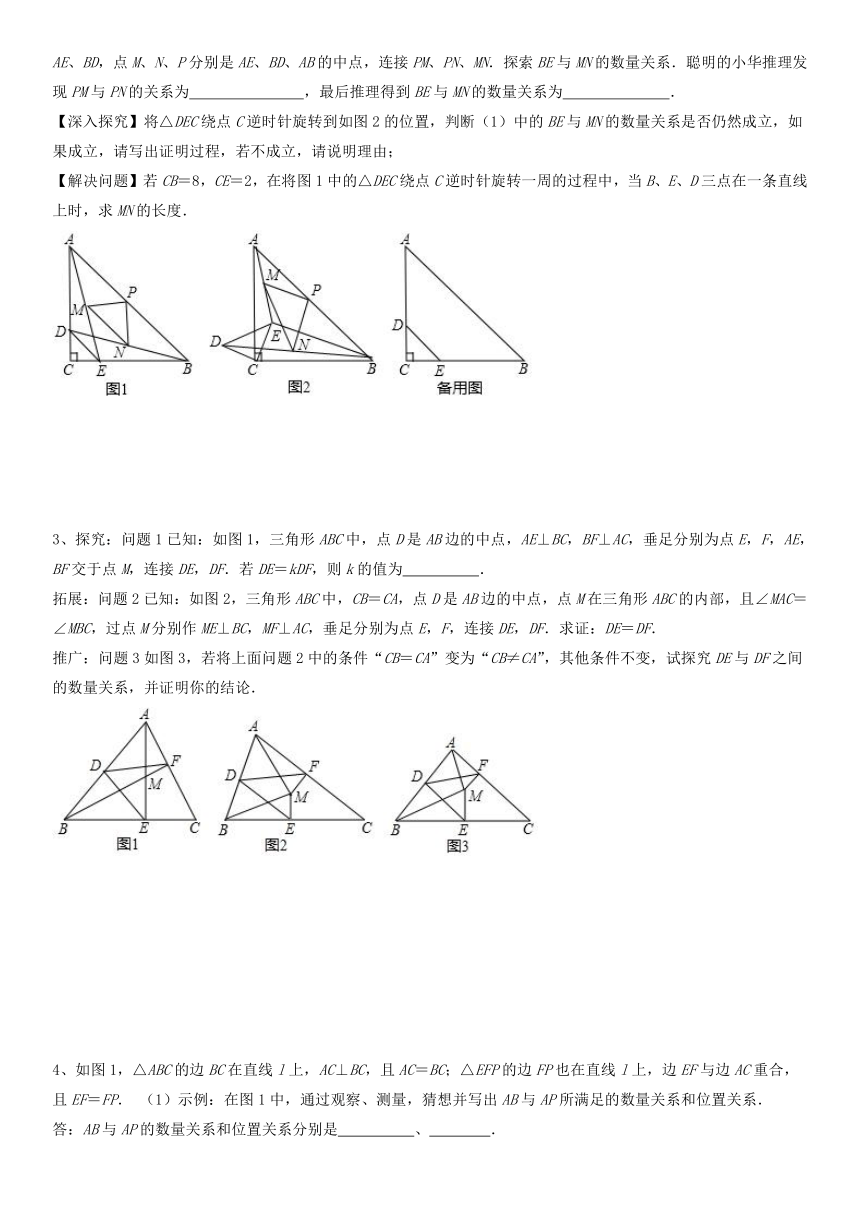
2、【问题探索】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在AC、BC边上,DC=EC,连接DE、AE、BD,点M、N、P分别是AE、BD、AB的中点,连接PM、PN、MN.探索BE与MN的数量关系.聪明的小华推理发现PM与PN的关系为 ,最后推理得到BE与MN的数量关系为 .
【深入探究】将△DEC绕点C逆时针旋转到如图2的位置,判断(1)中的BE与MN的数量关系是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
【解决问题】若CB=8,CE=2,在将图1中的△DEC绕点C逆时针旋转一周的过程中,当B、E、D三点在一条直线上时,求MN的长度.
3、探究:问题1已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展:问题2已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广:问题3如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
4、如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,
且EF=FP. (1)示例:在图1中,通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系.
答:AB与AP的数量关系和位置关系分别是 、 .
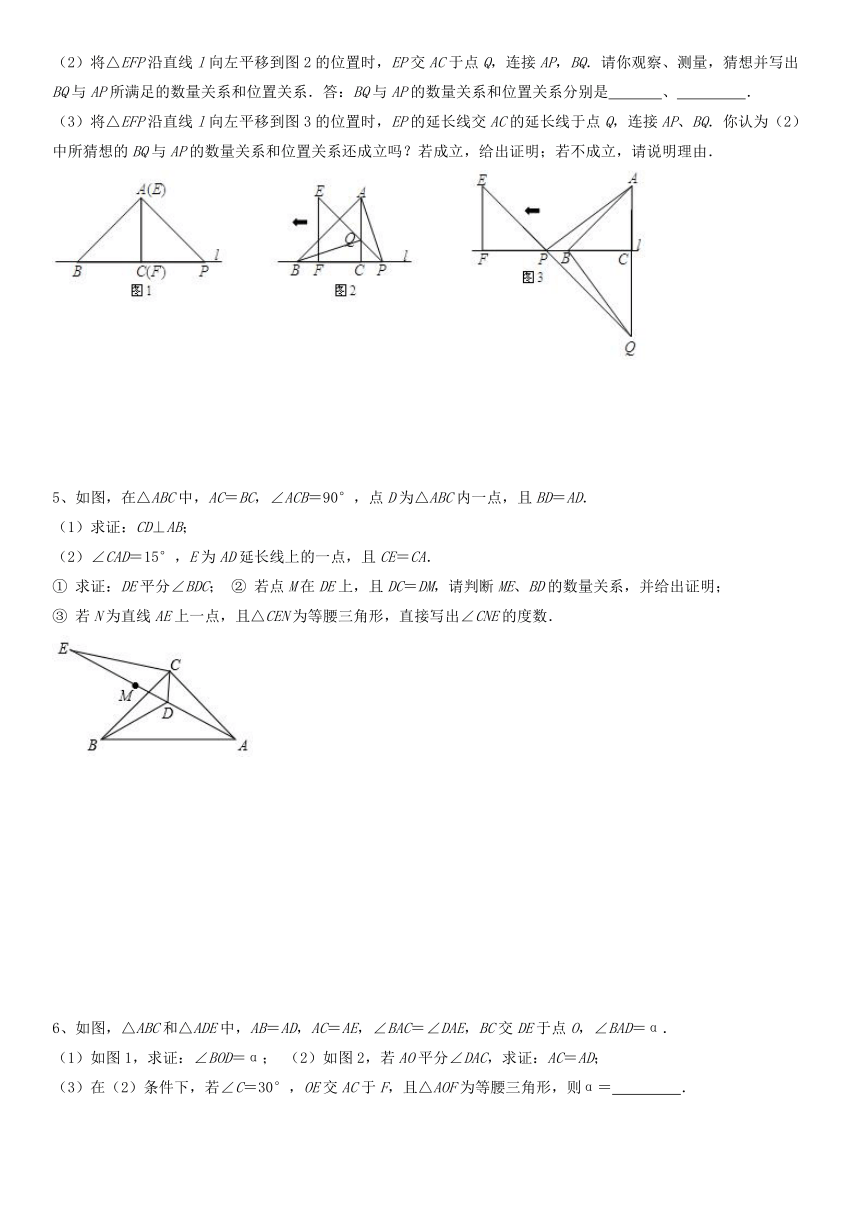
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.请你观察、测量,猜想并写出BQ与AP所满足的数量关系和位置关系.答:BQ与AP的数量关系和位置关系分别是 、 .
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
5、如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
① 求证:DE平分∠BDC; ② 若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③ 若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
6、如图,△ABC和△ADE中,AB=AD,AC=AE,∠BAC=∠DAE,BC交DE于点O,∠BAD=α.
(1)如图1,求证:∠BOD=α; (2)如图2,若AO平分∠DAC,求证:AC=AD;
(3)在(2)条件下,若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则α= .
7、已知:在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.
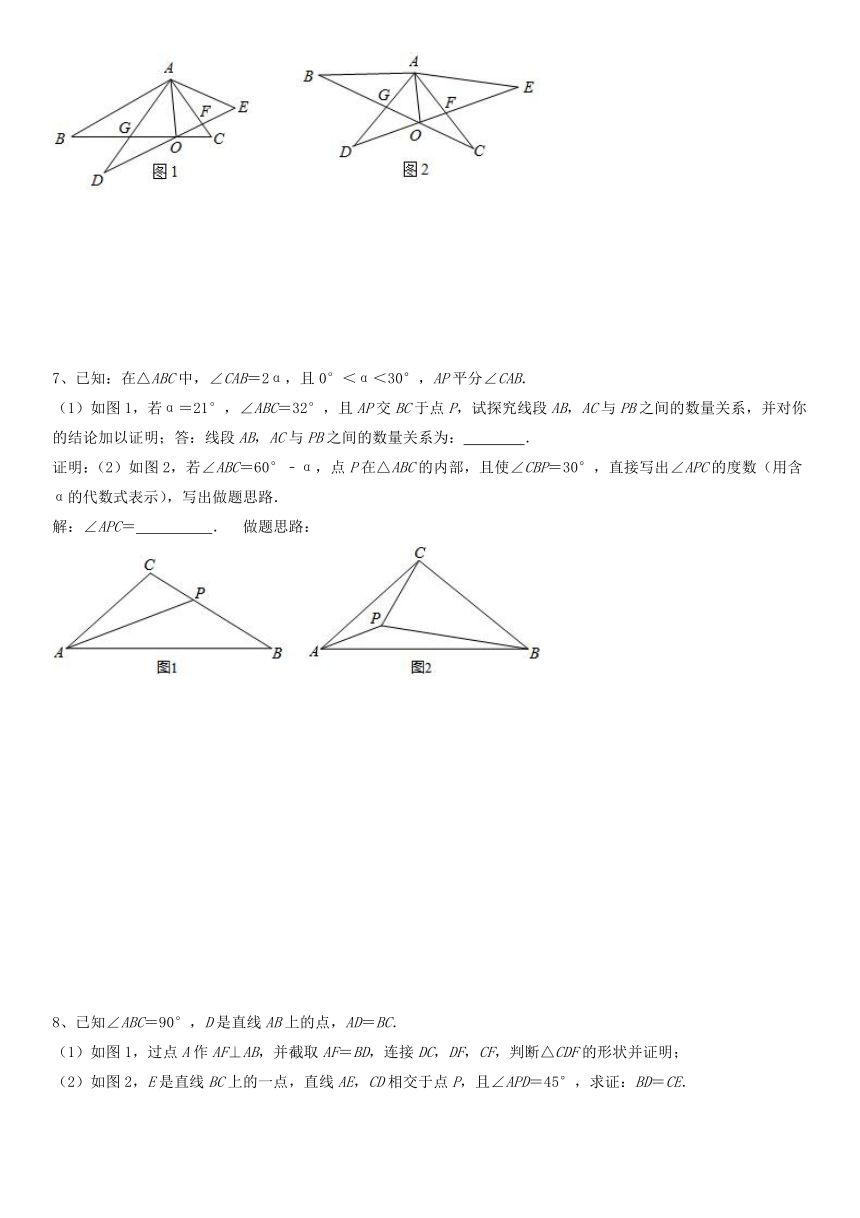
(1)如图1,若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明;答:线段AB,AC与PB之间的数量关系为: .
证明:(2)如图2,若∠ABC=60°﹣α,点P在△ABC的内部,且使∠CBP=30°,直接写出∠APC的度数(用含α的代数式表示),写出做题思路.
解:∠APC= . 做题思路:
8、已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.
9、如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB,点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.
(1)若∠AEF=20°,∠ADE=50°,BC=2,求AB的长度; (2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明你的结论.
10、(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.
【参考答案】
1、在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.
(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.
(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.
【解答】证明:(1)如图,在BC上截取BM=BD,连接FM,∵∠A=60,∴∠BFC=90°+60°÷2=120°,
∴∠BFD=60°,∵BE平分∠ABC,∴∠1=∠2,在△BFD和△BFM中,,∴△BFD≌△BFM(SAS),
∴∠BFM=∠BFD=60°,DF=MF,∴∠CFM=120°﹣60°=60°,∵∠CFE=∠BFD=60°,∴∠CFM=∠CFE,
∵CD平分∠ACB,∴∠3=∠4,又CF=CF,在△ECF和△MCF中,,∴△ECF≌△MCF(ASA),
∴EF=MF,∴DF=EF;
(2)∵BE⊥AC,CD⊥AB,∴∠BDF=∠CDA=90°,∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,
∴∠1=∠3,∵BD=CD,在△BDF和△CDA中,,∴△BDF≌△CDA(ASA),∴DF=DA,
∵∠ADF=90°,∴∠6=45°,∵∠G=∠6,∴∠5=45°∴∠G=∠5,∴GD=DA,∴GD=DF.
2、【问题探索】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在AC、BC边上,DC=EC,连接DE、AE、BD,点M、N、P分别是AE、BD、AB的中点,连接PM、PN、MN.探索BE与MN的数量关系.聪明的小华推理发现PM与PN的关系为 ,最后推理得到BE与MN的数量关系为 .
【深入探究】将△DEC绕点C逆时针旋转到如图2的位置,判断(1)中的BE与MN的数量关系是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
【解决问题】若CB=8,CE=2,在将图1中的△DEC绕点C逆时针旋转一周的过程中,当B、E、D三点在一条直线上时,求MN的长度.
【解答】解:(1)如图1中,∵AM=ME,AP=PB,∴PM∥BE,PM=BE,∵BN=DN,AP=PB,
∴PN∥AD,PN=AD,∵AC=BC,CD=CE,∴AD=BE,∴PM=PN,∵∠ACB=90°,∴AC⊥BC,
∵PM∥BC,PN∥AC,∴PM⊥PN,∴△PMN的等腰直角三角形,∴MN=PM,∴MN= BE,∴BE=MN,
故答案为PM=PN,PM⊥PN;BE=MN;
(2)如图2中,结论仍然成立.
理由:连接AD、延长BE交AD于点H.∵△ABC和△CDE是等腰直角三角形,
∴CD=CE,CA=CB,∠ACB=∠DCE=90°,∵∠ACB﹣∠ACE=∠DCE﹣∠ACE,∴∠ACD=∠ECB,∴△ECB≌△DCA,
∴BE=AD,∠DAC=∠EBC,∵∠AHB=180°﹣(∠HAB+∠ABH)=180°﹣(45°+∠HAC+∠ABH)
=∠180°﹣(45°+∠HBC+∠ABH)=180°﹣90°=90°,∴BH⊥AD,∵M、N、P分别为AE、BD、AB的中点,
∴PM∥BE,PM=BE,PN∥AD,PN=AD,∴PM=PN,∠MPN=90°,∴BE=2PM=2×MN=MN.
(3)① 如图3中,作CG⊥BD于G,则CG=GE=DG=,
当D、E、B共线时,在Rt△BCG中,BG===,
∴BE=BG﹣GE=﹣,∴MN=BE=﹣1.
② 如图4中,作CG⊥BD于G,则CG=GE=DG=,当D、E、B共线时,在Rt△BCG中,BG=,
∴BE=BG+GE=+,∴MN=BE=+1.故答案为 ﹣1或 +1.
3、探究:问题1已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展:问题2已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广:问题3如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
【解答】解:(1)∵AE⊥BC,BF⊥AC,∴△AEB和△AFB都是直角三角形,∵D是AB的中点
∴DE和DF分别为Rt△AEB和Rt△AFB的斜边中线,∴DE=AB,DF=AB(直角三角形斜边中线等于斜边的一半)
∴DE=DF,∵DE=kDF,∴k=1;
(2)∵CB=CA,∴∠CBA=∠CAB,∵∠MAC=∠MBE,∴∠CBA﹣∠MBC=∠CAB﹣∠MAC,即∠ABM=∠BAM
∴AM=BM,∵ME⊥BC,MF⊥AC,∴∠MEB=∠MFA=90,又∵∠MBE=∠MAF,∴△MEB≌△MFA(AAS)
∴BE=AF,∵D是AB的中点,即BD=AD,又∵∠DBE=∠DAF,∴△DBE≌△DAF(SAS),∴DE=DF;
(3)DE=DF。如图1,作AM的中点G,BM的中点H,∵点 D是 边 AB的 中点,∴DG∥BM,DG=BM
同理可得:DH∥AM,DH=AM,∵ME⊥BC于E,H 是BM的中点,∴在Rt△BEM中,HE=BM=BH
∴∠HBE=∠HEB,∠MHE=∠HBE+∠HEB=2∠MBC,又∵DG=BM,HE=BM,∴DG=HE
同理可得:DH=FG,∠MGF=2∠MAC,∵DG∥BM,DH∥GM,∴四边形DHMG是平行四边形,∴∠DGM=∠DHM
∵∠MGF=2∠MAC,∠MHE=2∠MBC,又∵∠MBC=∠MAC,∴∠MGF=∠MHE,∴∠DGM+∠MGF=∠DHM+∠MHE
∴∠DGF=∠DHE,在△DHE与△FGD中,,∴△DHE≌△FGD(SAS),∴DE=DF.
4、如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,
且EF=FP. (1)示例:在图1中,通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系.
答:AB与AP的数量关系和位置关系分别是 、 .
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.请你观察、测量,猜想并写出BQ与AP所满足的数量关系和位置关系.答:BQ与AP的数量关系和位置关系分别是 、 .
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
【解答】解:(1)AB=AP,AB⊥AP; (2)BQ=AP,BQ⊥AP;
(3)成立.证明:如图,∵∠EPF=45°,∴∠CPQ=45°.∵AC⊥BC,∴∠CQP=∠CPQ,CQ=CP.
在Rt△BCQ和Rt△ACP中,∴Rt△BCQ≌Rt△ACP(SAS)∴BQ=AP;延长QB交AP于点N,
∴∠PBN=∠CBQ.∵Rt△BCQ≌Rt△ACP,∴∠BQC=∠APC.在Rt△BCQ中,∠BQC+∠CBQ=90°,
∴∠APC+∠PBN=90°.∴∠PNB=90°.∴QB⊥AP.
5、如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
① 求证:DE平分∠BDC; ② 若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③ 若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
【解答】证明:(1)∵CB=CA,DB=DA,∴CD垂直平分线段AB,∴CD⊥AB.
(2)① 证明:∵AC=BC,∴∠CBA=∠CAB,又∵∠ACB=90°,∴∠CBA=∠CAB=45°,
又∵∠CAD=∠CBD=15°,∴∠DBA=∠DAB=30°,∴∠BDE=30°+30°=60°,
∵AC=BC,∠CAD=∠CBD=15°,BD=AD,在△ADC和△BDC中,,∴△ADC≌△BDC(SAS),
∴∠ACD=∠BCD=45°,∴∠CDE=60°,∵∠CDE=∠BDE=60°,∴DE平分∠BDC;
② 解:结论:ME=BD,
理由:连接MC,∵DC=DM,∠CDE=60°,∴△MCD为等边三角形,∴CM=CD,∵EC=CA,∠EMC=120°,
∴∠ECM=∠BCD=45°在△BDC和△EMC中,,∴△BDC≌△EMC(SAS),∴ME=BD.
③ 当EN=EC时,∠ENC=7.5°或82.5°;当EN=CN时,∠ENC=150°;当CE=CN时,∠CNE=15°,
所以∠CNE的度数为7.5°、15°、82.5°、150°.
6、如图,△ABC和△ADE中,AB=AD,AC=AE,∠BAC=∠DAE,BC交DE于点O,∠BAD=α.
(1)如图1,求证:∠BOD=α; (2)如图2,若AO平分∠DAC,求证:AC=AD;
(3)在(2)条件下,若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则α= .
【解答】证明:(1)设AD交OB于K.在△ABC和△ADE中,∴△ABC≌△ADE(SAS),
∴∠B=∠D,∵∠AKB=∠DKO,∴∠BOD=∠BAD=α
(2)过A作AM⊥BC于M,作AN⊥DE于N∵△ABC≌△ADE,∴S△ABC=S△ADE,∴,
∵BC=DE,∴AM=AN∴AO平分∠BOE,∵AO平分∠DAC,∴∠DAO=∠CAO,∴∠BAO=∠EAO
在△ABO和△AEO中,,∴△ABO≌△AEO(ASA)∴AB=AE,∵AB=AD,AC=AE,∴AC=AD,
(3)由(2)可知∠AOB=∠AOF,∴∠AOF≠∠OAF(否则CA∥CB),∴只有AO=AF或OA=OF,
① 当AO=AF时,∠AOF=∠AFO=∠AOB=α+30°,∴∠AOB+∠AOF+∠FOC=180°,
∴2(α+30)+α=180°,∴α=40°.
② 当OA=OF时,∠OAF=∠OFA=α+30°,∴∠AOB=∠AOF=180°﹣2(α+30°),
∴2[180°﹣2(α+30)]+α=180°,∴α=20°,综上所述,α=40°或20°
7、已知:在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.
(1)如图1,若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明;答:线段AB,AC与PB之间的数量关系为: .
证明:(2)如图2,若∠ABC=60°﹣α,点P在△ABC的内部,且使∠CBP=30°,直接写出∠APC的度数(用含α的代数式表示),写出做题思路.
解:∠APC= . 做题思路:
【解答】解:(1)AB﹣AC=PB,
证明:在AB上截取AD,使AD=AC.连PD,∵AP平分∠CAB,∴∠CAP=∠BAP,
在△ACP和△ADP中,,∴△ACP≌△ADP(SAS),∴∠C=∠ADP.
∵△ABC中,∠CAB=42°,∠ABC=32°,∴∠C=180°﹣∠CAB﹣∠ABC=180°﹣42°﹣32°=106°.
∴∠ADP=106°.∴∠BDP=180°﹣∠ADP=180°﹣106°=74°,∠BPD=∠ADP﹣∠ABC=106°﹣32°=74°.
∴∠BDP=∠BPD.∴PB=DB,∴AB﹣AC=AB﹣AD=DB=PB;
(2)延长AC至M,使AM=AB,连接PM,BM,∵AP平分∠CAB,∠CAB=2α,∴∠CAP=∠BAP=×2α=α.
在△AMP和△ABP中,,∴△AMP≌△ABP(SAS)∴PM=PB,∠ABP=∠AMP.
∵∠ABC=60°﹣α,∠CBP=30°,∴∠ABP=(60°﹣α)﹣30°=30°﹣α.∴∠AMP=∠ABP=30°﹣α.
△AMB中,AM=AB,∴∠AMB=∠ABM=(180°﹣∠MAB)÷2=(180°﹣2)÷2=90°﹣α.
∴∠PMB=∠AMB﹣∠AMP=(90°﹣α)﹣(30°﹣α)=60°.∴△PMB为等边三角形.
∵∠CBM=∠ABM﹣∠ABC=(90°﹣α)﹣(60°﹣α)=30°,∴∠CBM=∠CBP.
∴BC平分∠PBM.∴BC垂直平分PM.∴CP=CM.∴∠CPM=∠CMP=30°﹣α.
∴∠ACP=∠CPM+∠CMP=(30°﹣α)+(30°﹣α)=60°﹣2α.
∴△ACP中,∠APC=180°﹣∠PAM﹣∠ACP=180°﹣α﹣(60°﹣2α)=120°+α.
故答案为:(1)AB﹣AC=PB;(2)120°+α.
8、已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.
【解答】解:(1)∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,在△FAD与△DBC中,,
∴△FAD≌△DBC(SAS);∴FD=DC,∴△CDF是等腰三角形,∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,∴△CDF是等腰直角三角形.
(2)如图2,作AF⊥AB于A,使AF=BD,连接DF,CF,∴∠FAD=90°.∵∠ABC=90°,
∴∠FAD=∠DBC=90°.在△FAD和△DBC中,,∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD.∵∠BDC+∠BCD=90°,∴∠ADF+∠BDC=90°,∴∠FDC=90°,∴∠FCD=45°.
∵∠APD=45°,∴∠FCD=∠APD,∴CF∥AE.∵∠FAD=90°,∠ABC=90,∴∠FAD=∠ABC,
∴AF∥BC.∴四边形AECF是平行四边形,∴AF=CE,∴CE=BD.
9、如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB,点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.
(1)若∠AEF=20°,∠ADE=50°,BC=2,求AB的长度; (2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明你的结论.
【解答】解:(1)在等腰直角三角形DEF中,∠DEF=90°,∵∠1=20°,∴∠2=∠DEF﹣∠1=70°,
∵∠EDA+∠2+∠3=180°,∴∠3=60°,∵EA⊥AB,∴∠EAB=90°,
∵∠3+∠EAB+∠A=180°,∴∠4=30°,∵∠C=90°,∴AB=2BC=4;
(2)如图1,过D作DM⊥AE于M,在△DEM中,∠2+∠5=90°,∵∠2+∠1=90°,∴∠1=∠5,∵DE=FE,
在△DEM与△EFA中,,∴△DEM≌△EFA,∴AF=EM,∵∠4+∠B=90°,
∵∠3+∠EAB+∠4=180°,∴∠3+∠4=90°,∴∠3=∠B,在△DAM与△ABC中,,
∴△DAM≌△ABC,∴BC=AM,∴AE=EM+AM=AF+BC;
(3)如图2,过D作DM⊥AE交AE的延长线于M,∵∠C=90°,∴∠1+∠B=90°,
∵∠2+∠MAB+∠1=180°,∠MAB=90°,∴∠2+∠1=90°,∠2=∠B,在△ADM与△BAC中,,
∴△ADM≌△BAC,∴BC=AM,∵EF=DE,∠DEF=90°,∵∠3+∠DEF+∠4=180°,∴∠3+∠4=90°,
∵∠3+∠5=90°,∴∠4=∠5,在△MED与△AFE中,,∴△MED≌△AFE,
∴ME=AF,∴AE+AF=AE+ME=AM=BC,即AE+AF=BC.
10、(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.
【解答】解:(1)∵BD⊥l,CE⊥l,∴∠BDA=∠AEC=90°又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD,在△ABD和△CAE中,,
∴△ABD≌△CAE(AAS)∴BD=AE,AD=CE,∵DE=AD+AE,∴DE=CE+BD;
(2)成立
∵∠BDA=∠AEC=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠CAE=∠ABD,
在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴BD+CE=AE+AD=DE;
(3)由(2)知,△ADB≌△CAE,∴BD=EA,∠DBA=∠CAE,∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE,∵BF=AF
在△DBF和△EAF中,,∴△DBF≌△EAF(SAS),∴DF=EF。
1.5三角形全等的判定
【知识点-部分】
一、全等三角形判定1——“边边边”
1、三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).
二、全等三角形判定2——“边角边”
1、两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).
2、有两边和其中一边的对角对应相等,两个三角形不一定全等.
三、全等三角形判定3——“角边角”
1、两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。
四、全等三角形判定4——“角角边”
1、两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)
2、由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论。
【典型例题-精选部分】
1、在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.
(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.
(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.
2、【问题探索】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在AC、BC边上,DC=EC,连接DE、AE、BD,点M、N、P分别是AE、BD、AB的中点,连接PM、PN、MN.探索BE与MN的数量关系.聪明的小华推理发现PM与PN的关系为 ,最后推理得到BE与MN的数量关系为 .
【深入探究】将△DEC绕点C逆时针旋转到如图2的位置,判断(1)中的BE与MN的数量关系是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
【解决问题】若CB=8,CE=2,在将图1中的△DEC绕点C逆时针旋转一周的过程中,当B、E、D三点在一条直线上时,求MN的长度.
3、探究:问题1已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展:问题2已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广:问题3如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
4、如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,
且EF=FP. (1)示例:在图1中,通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系.
答:AB与AP的数量关系和位置关系分别是 、 .
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.请你观察、测量,猜想并写出BQ与AP所满足的数量关系和位置关系.答:BQ与AP的数量关系和位置关系分别是 、 .
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
5、如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
① 求证:DE平分∠BDC; ② 若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③ 若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
6、如图,△ABC和△ADE中,AB=AD,AC=AE,∠BAC=∠DAE,BC交DE于点O,∠BAD=α.
(1)如图1,求证:∠BOD=α; (2)如图2,若AO平分∠DAC,求证:AC=AD;
(3)在(2)条件下,若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则α= .
7、已知:在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.
(1)如图1,若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明;答:线段AB,AC与PB之间的数量关系为: .
证明:(2)如图2,若∠ABC=60°﹣α,点P在△ABC的内部,且使∠CBP=30°,直接写出∠APC的度数(用含α的代数式表示),写出做题思路.
解:∠APC= . 做题思路:
8、已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.
9、如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB,点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.
(1)若∠AEF=20°,∠ADE=50°,BC=2,求AB的长度; (2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明你的结论.
10、(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.
【参考答案】
1、在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.
(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.
(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.
【解答】证明:(1)如图,在BC上截取BM=BD,连接FM,∵∠A=60,∴∠BFC=90°+60°÷2=120°,
∴∠BFD=60°,∵BE平分∠ABC,∴∠1=∠2,在△BFD和△BFM中,,∴△BFD≌△BFM(SAS),
∴∠BFM=∠BFD=60°,DF=MF,∴∠CFM=120°﹣60°=60°,∵∠CFE=∠BFD=60°,∴∠CFM=∠CFE,
∵CD平分∠ACB,∴∠3=∠4,又CF=CF,在△ECF和△MCF中,,∴△ECF≌△MCF(ASA),
∴EF=MF,∴DF=EF;
(2)∵BE⊥AC,CD⊥AB,∴∠BDF=∠CDA=90°,∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,
∴∠1=∠3,∵BD=CD,在△BDF和△CDA中,,∴△BDF≌△CDA(ASA),∴DF=DA,
∵∠ADF=90°,∴∠6=45°,∵∠G=∠6,∴∠5=45°∴∠G=∠5,∴GD=DA,∴GD=DF.
2、【问题探索】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在AC、BC边上,DC=EC,连接DE、AE、BD,点M、N、P分别是AE、BD、AB的中点,连接PM、PN、MN.探索BE与MN的数量关系.聪明的小华推理发现PM与PN的关系为 ,最后推理得到BE与MN的数量关系为 .
【深入探究】将△DEC绕点C逆时针旋转到如图2的位置,判断(1)中的BE与MN的数量关系是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
【解决问题】若CB=8,CE=2,在将图1中的△DEC绕点C逆时针旋转一周的过程中,当B、E、D三点在一条直线上时,求MN的长度.
【解答】解:(1)如图1中,∵AM=ME,AP=PB,∴PM∥BE,PM=BE,∵BN=DN,AP=PB,
∴PN∥AD,PN=AD,∵AC=BC,CD=CE,∴AD=BE,∴PM=PN,∵∠ACB=90°,∴AC⊥BC,
∵PM∥BC,PN∥AC,∴PM⊥PN,∴△PMN的等腰直角三角形,∴MN=PM,∴MN= BE,∴BE=MN,
故答案为PM=PN,PM⊥PN;BE=MN;
(2)如图2中,结论仍然成立.
理由:连接AD、延长BE交AD于点H.∵△ABC和△CDE是等腰直角三角形,
∴CD=CE,CA=CB,∠ACB=∠DCE=90°,∵∠ACB﹣∠ACE=∠DCE﹣∠ACE,∴∠ACD=∠ECB,∴△ECB≌△DCA,
∴BE=AD,∠DAC=∠EBC,∵∠AHB=180°﹣(∠HAB+∠ABH)=180°﹣(45°+∠HAC+∠ABH)
=∠180°﹣(45°+∠HBC+∠ABH)=180°﹣90°=90°,∴BH⊥AD,∵M、N、P分别为AE、BD、AB的中点,
∴PM∥BE,PM=BE,PN∥AD,PN=AD,∴PM=PN,∠MPN=90°,∴BE=2PM=2×MN=MN.
(3)① 如图3中,作CG⊥BD于G,则CG=GE=DG=,
当D、E、B共线时,在Rt△BCG中,BG===,
∴BE=BG﹣GE=﹣,∴MN=BE=﹣1.
② 如图4中,作CG⊥BD于G,则CG=GE=DG=,当D、E、B共线时,在Rt△BCG中,BG=,
∴BE=BG+GE=+,∴MN=BE=+1.故答案为 ﹣1或 +1.
3、探究:问题1已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展:问题2已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广:问题3如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
【解答】解:(1)∵AE⊥BC,BF⊥AC,∴△AEB和△AFB都是直角三角形,∵D是AB的中点
∴DE和DF分别为Rt△AEB和Rt△AFB的斜边中线,∴DE=AB,DF=AB(直角三角形斜边中线等于斜边的一半)
∴DE=DF,∵DE=kDF,∴k=1;
(2)∵CB=CA,∴∠CBA=∠CAB,∵∠MAC=∠MBE,∴∠CBA﹣∠MBC=∠CAB﹣∠MAC,即∠ABM=∠BAM
∴AM=BM,∵ME⊥BC,MF⊥AC,∴∠MEB=∠MFA=90,又∵∠MBE=∠MAF,∴△MEB≌△MFA(AAS)
∴BE=AF,∵D是AB的中点,即BD=AD,又∵∠DBE=∠DAF,∴△DBE≌△DAF(SAS),∴DE=DF;
(3)DE=DF。如图1,作AM的中点G,BM的中点H,∵点 D是 边 AB的 中点,∴DG∥BM,DG=BM
同理可得:DH∥AM,DH=AM,∵ME⊥BC于E,H 是BM的中点,∴在Rt△BEM中,HE=BM=BH
∴∠HBE=∠HEB,∠MHE=∠HBE+∠HEB=2∠MBC,又∵DG=BM,HE=BM,∴DG=HE
同理可得:DH=FG,∠MGF=2∠MAC,∵DG∥BM,DH∥GM,∴四边形DHMG是平行四边形,∴∠DGM=∠DHM
∵∠MGF=2∠MAC,∠MHE=2∠MBC,又∵∠MBC=∠MAC,∴∠MGF=∠MHE,∴∠DGM+∠MGF=∠DHM+∠MHE
∴∠DGF=∠DHE,在△DHE与△FGD中,,∴△DHE≌△FGD(SAS),∴DE=DF.
4、如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,
且EF=FP. (1)示例:在图1中,通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系.
答:AB与AP的数量关系和位置关系分别是 、 .
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.请你观察、测量,猜想并写出BQ与AP所满足的数量关系和位置关系.答:BQ与AP的数量关系和位置关系分别是 、 .
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
【解答】解:(1)AB=AP,AB⊥AP; (2)BQ=AP,BQ⊥AP;
(3)成立.证明:如图,∵∠EPF=45°,∴∠CPQ=45°.∵AC⊥BC,∴∠CQP=∠CPQ,CQ=CP.
在Rt△BCQ和Rt△ACP中,∴Rt△BCQ≌Rt△ACP(SAS)∴BQ=AP;延长QB交AP于点N,
∴∠PBN=∠CBQ.∵Rt△BCQ≌Rt△ACP,∴∠BQC=∠APC.在Rt△BCQ中,∠BQC+∠CBQ=90°,
∴∠APC+∠PBN=90°.∴∠PNB=90°.∴QB⊥AP.
5、如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
① 求证:DE平分∠BDC; ② 若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③ 若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
【解答】证明:(1)∵CB=CA,DB=DA,∴CD垂直平分线段AB,∴CD⊥AB.
(2)① 证明:∵AC=BC,∴∠CBA=∠CAB,又∵∠ACB=90°,∴∠CBA=∠CAB=45°,
又∵∠CAD=∠CBD=15°,∴∠DBA=∠DAB=30°,∴∠BDE=30°+30°=60°,
∵AC=BC,∠CAD=∠CBD=15°,BD=AD,在△ADC和△BDC中,,∴△ADC≌△BDC(SAS),
∴∠ACD=∠BCD=45°,∴∠CDE=60°,∵∠CDE=∠BDE=60°,∴DE平分∠BDC;
② 解:结论:ME=BD,
理由:连接MC,∵DC=DM,∠CDE=60°,∴△MCD为等边三角形,∴CM=CD,∵EC=CA,∠EMC=120°,
∴∠ECM=∠BCD=45°在△BDC和△EMC中,,∴△BDC≌△EMC(SAS),∴ME=BD.
③ 当EN=EC时,∠ENC=7.5°或82.5°;当EN=CN时,∠ENC=150°;当CE=CN时,∠CNE=15°,
所以∠CNE的度数为7.5°、15°、82.5°、150°.
6、如图,△ABC和△ADE中,AB=AD,AC=AE,∠BAC=∠DAE,BC交DE于点O,∠BAD=α.
(1)如图1,求证:∠BOD=α; (2)如图2,若AO平分∠DAC,求证:AC=AD;
(3)在(2)条件下,若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则α= .
【解答】证明:(1)设AD交OB于K.在△ABC和△ADE中,∴△ABC≌△ADE(SAS),
∴∠B=∠D,∵∠AKB=∠DKO,∴∠BOD=∠BAD=α
(2)过A作AM⊥BC于M,作AN⊥DE于N∵△ABC≌△ADE,∴S△ABC=S△ADE,∴,
∵BC=DE,∴AM=AN∴AO平分∠BOE,∵AO平分∠DAC,∴∠DAO=∠CAO,∴∠BAO=∠EAO
在△ABO和△AEO中,,∴△ABO≌△AEO(ASA)∴AB=AE,∵AB=AD,AC=AE,∴AC=AD,
(3)由(2)可知∠AOB=∠AOF,∴∠AOF≠∠OAF(否则CA∥CB),∴只有AO=AF或OA=OF,
① 当AO=AF时,∠AOF=∠AFO=∠AOB=α+30°,∴∠AOB+∠AOF+∠FOC=180°,
∴2(α+30)+α=180°,∴α=40°.
② 当OA=OF时,∠OAF=∠OFA=α+30°,∴∠AOB=∠AOF=180°﹣2(α+30°),
∴2[180°﹣2(α+30)]+α=180°,∴α=20°,综上所述,α=40°或20°
7、已知:在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.
(1)如图1,若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明;答:线段AB,AC与PB之间的数量关系为: .
证明:(2)如图2,若∠ABC=60°﹣α,点P在△ABC的内部,且使∠CBP=30°,直接写出∠APC的度数(用含α的代数式表示),写出做题思路.
解:∠APC= . 做题思路:
【解答】解:(1)AB﹣AC=PB,
证明:在AB上截取AD,使AD=AC.连PD,∵AP平分∠CAB,∴∠CAP=∠BAP,
在△ACP和△ADP中,,∴△ACP≌△ADP(SAS),∴∠C=∠ADP.
∵△ABC中,∠CAB=42°,∠ABC=32°,∴∠C=180°﹣∠CAB﹣∠ABC=180°﹣42°﹣32°=106°.
∴∠ADP=106°.∴∠BDP=180°﹣∠ADP=180°﹣106°=74°,∠BPD=∠ADP﹣∠ABC=106°﹣32°=74°.
∴∠BDP=∠BPD.∴PB=DB,∴AB﹣AC=AB﹣AD=DB=PB;
(2)延长AC至M,使AM=AB,连接PM,BM,∵AP平分∠CAB,∠CAB=2α,∴∠CAP=∠BAP=×2α=α.
在△AMP和△ABP中,,∴△AMP≌△ABP(SAS)∴PM=PB,∠ABP=∠AMP.
∵∠ABC=60°﹣α,∠CBP=30°,∴∠ABP=(60°﹣α)﹣30°=30°﹣α.∴∠AMP=∠ABP=30°﹣α.
△AMB中,AM=AB,∴∠AMB=∠ABM=(180°﹣∠MAB)÷2=(180°﹣2)÷2=90°﹣α.
∴∠PMB=∠AMB﹣∠AMP=(90°﹣α)﹣(30°﹣α)=60°.∴△PMB为等边三角形.
∵∠CBM=∠ABM﹣∠ABC=(90°﹣α)﹣(60°﹣α)=30°,∴∠CBM=∠CBP.
∴BC平分∠PBM.∴BC垂直平分PM.∴CP=CM.∴∠CPM=∠CMP=30°﹣α.
∴∠ACP=∠CPM+∠CMP=(30°﹣α)+(30°﹣α)=60°﹣2α.
∴△ACP中,∠APC=180°﹣∠PAM﹣∠ACP=180°﹣α﹣(60°﹣2α)=120°+α.
故答案为:(1)AB﹣AC=PB;(2)120°+α.
8、已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上的一点,直线AE,CD相交于点P,且∠APD=45°,求证:BD=CE.
【解答】解:(1)∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,在△FAD与△DBC中,,
∴△FAD≌△DBC(SAS);∴FD=DC,∴△CDF是等腰三角形,∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,∴△CDF是等腰直角三角形.
(2)如图2,作AF⊥AB于A,使AF=BD,连接DF,CF,∴∠FAD=90°.∵∠ABC=90°,
∴∠FAD=∠DBC=90°.在△FAD和△DBC中,,∴△FAD≌△DBC(SAS),
∴DF=DC,∠ADF=∠BCD.∵∠BDC+∠BCD=90°,∴∠ADF+∠BDC=90°,∴∠FDC=90°,∴∠FCD=45°.
∵∠APD=45°,∴∠FCD=∠APD,∴CF∥AE.∵∠FAD=90°,∠ABC=90,∴∠FAD=∠ABC,
∴AF∥BC.∴四边形AECF是平行四边形,∴AF=CE,∴CE=BD.
9、如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB,点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.
(1)若∠AEF=20°,∠ADE=50°,BC=2,求AB的长度; (2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明你的结论.
【解答】解:(1)在等腰直角三角形DEF中,∠DEF=90°,∵∠1=20°,∴∠2=∠DEF﹣∠1=70°,
∵∠EDA+∠2+∠3=180°,∴∠3=60°,∵EA⊥AB,∴∠EAB=90°,
∵∠3+∠EAB+∠A=180°,∴∠4=30°,∵∠C=90°,∴AB=2BC=4;
(2)如图1,过D作DM⊥AE于M,在△DEM中,∠2+∠5=90°,∵∠2+∠1=90°,∴∠1=∠5,∵DE=FE,
在△DEM与△EFA中,,∴△DEM≌△EFA,∴AF=EM,∵∠4+∠B=90°,
∵∠3+∠EAB+∠4=180°,∴∠3+∠4=90°,∴∠3=∠B,在△DAM与△ABC中,,
∴△DAM≌△ABC,∴BC=AM,∴AE=EM+AM=AF+BC;
(3)如图2,过D作DM⊥AE交AE的延长线于M,∵∠C=90°,∴∠1+∠B=90°,
∵∠2+∠MAB+∠1=180°,∠MAB=90°,∴∠2+∠1=90°,∠2=∠B,在△ADM与△BAC中,,
∴△ADM≌△BAC,∴BC=AM,∵EF=DE,∠DEF=90°,∵∠3+∠DEF+∠4=180°,∴∠3+∠4=90°,
∵∠3+∠5=90°,∴∠4=∠5,在△MED与△AFE中,,∴△MED≌△AFE,
∴ME=AF,∴AE+AF=AE+ME=AM=BC,即AE+AF=BC.
10、(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.
【解答】解:(1)∵BD⊥l,CE⊥l,∴∠BDA=∠AEC=90°又∵∠BAC=90°,
∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD,在△ABD和△CAE中,,
∴△ABD≌△CAE(AAS)∴BD=AE,AD=CE,∵DE=AD+AE,∴DE=CE+BD;
(2)成立
∵∠BDA=∠AEC=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠CAE=∠ABD,
在△ADB和△CEA中,,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴BD+CE=AE+AD=DE;
(3)由(2)知,△ADB≌△CAE,∴BD=EA,∠DBA=∠CAE,∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE,∵BF=AF
在△DBF和△EAF中,,∴△DBF≌△EAF(SAS),∴DF=EF。
