河南省北大公学禹州国际学校2022-2023学年高二上学期9月开学考试数学试题(Word版含答案)
文档属性
| 名称 | 河南省北大公学禹州国际学校2022-2023学年高二上学期9月开学考试数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 448.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 18:08:14 | ||
图片预览


文档简介
北大公学禹州国际学校2022-2023学年高二上学期9月开学考试
数学试题
一、单选题
1. 在三棱锥中,,,,是边长为的等边三角形,点E为棱的中点,则三棱锥的体积为( )
A. B. C. D.
2. 如图,平面平面是等边三角形,四边形是矩形,且,E是的中点,F是上一点,当时,( )
A. 3 B. C. D. 2
3. 在下列条件中,一定能使空间中的四点共面的是( )
A. B.
C. D.
4. 如图,在大小为45°的二面角A EF D中,四边形ABFE,CDEF都是边长为1的正方形,则B,D两点间的距离是( )
A B.
C. 1 D.
5. 在中,角,,对边分别为,,,若,,则面积的最大值为( )
A. 1 B. C. 2 D.
6. 已知的内角所对的边分别为满足且,则( )
A. B. C. D.
7. 已知P为空间中任意一点,A、B、C、D四点满足任意三点均不共线,但四点共面,且,则实数x的值为( )
A. B. C. D.
8. 锐角中,若,则的取值范围是( )
A. B. C. D.
二、填空题
9. 已知空间向量,,,若,,共面,则______.
10. 在四面体ABCD中,,,,且,则几何体ABCD的外接球的体积为______.
11. 在三棱锥中,侧棱、、两两垂直,、、的面积分别为、、,则三棱锥的外接球的体积为__________.
12. 已知空间向量,,且与垂直,则等于 ___.
13. 已知点,,,若,,三点共线,则______.
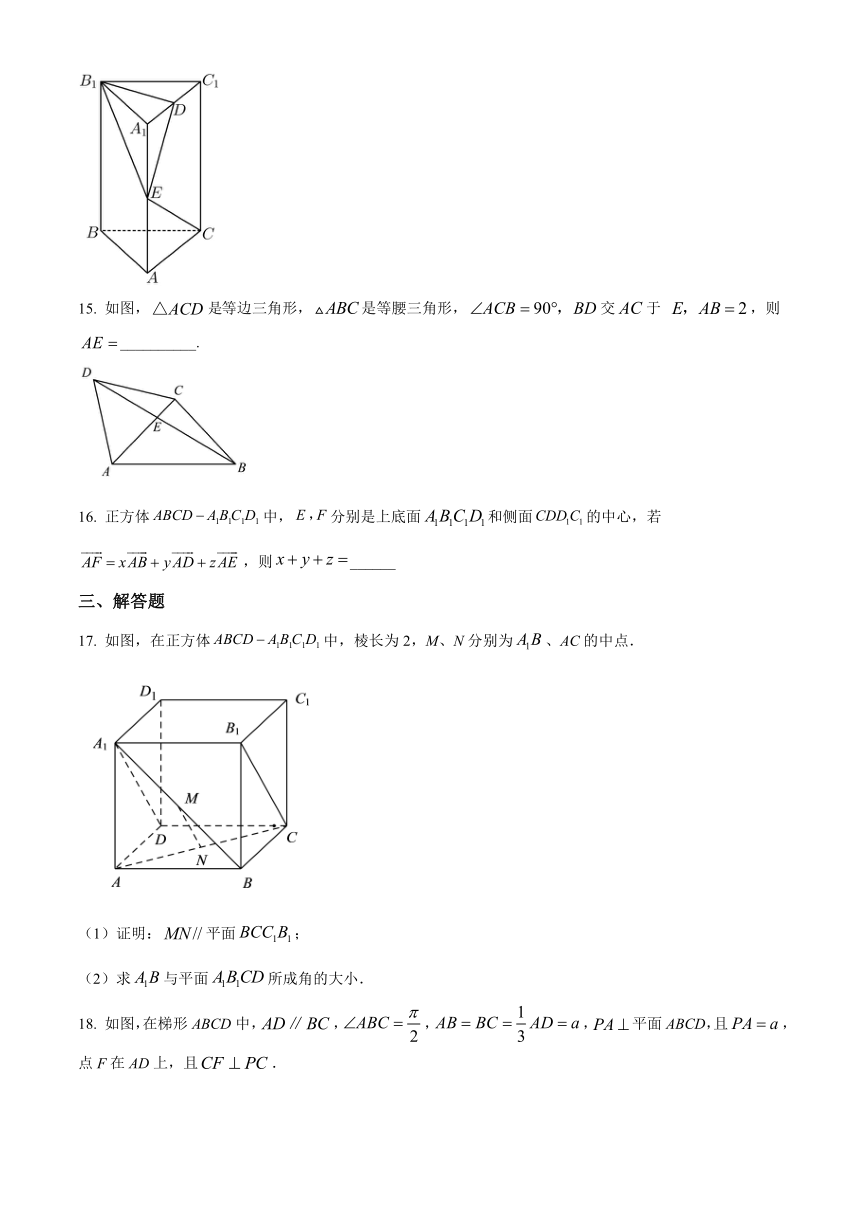
14. 如图所示,在直三棱柱中,底面是以ABC为直角的等腰三角形,,,是的中点,点在棱上,要使平面,则___________.
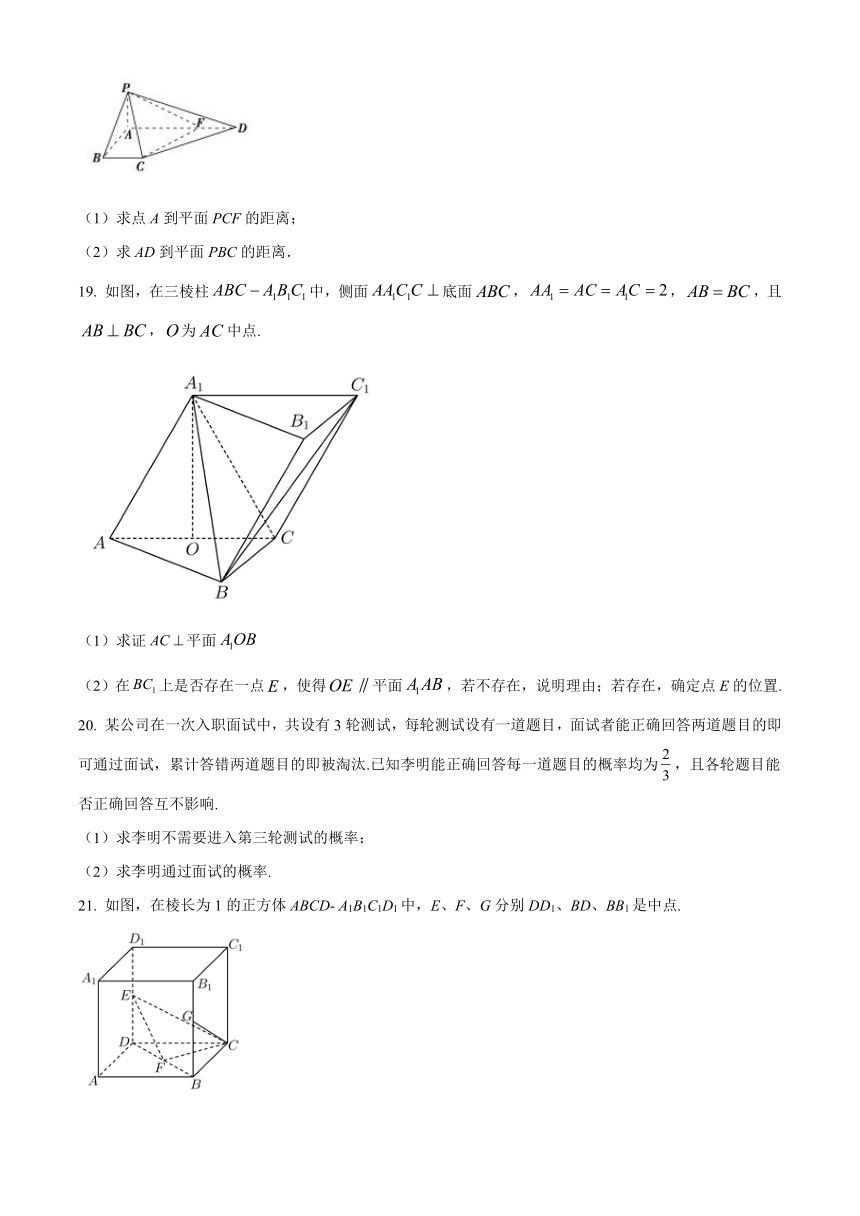
15. 如图,等边三角形,是等腰三角形,交于 ,则__________.
16. 正方体中,分别是上底面和侧面的中心,若,则______
三、解答题
17. 如图,在正方体中,棱长为2,M、N分别为、AC的中点.
(1)证明:平面;
(2)求与平面所成角的大小.
18. 如图,在梯形ABCD中,,,,平面ABCD,且,点F在AD上,且.
(1)求点A到平面PCF的距离;
(2)求AD到平面PBC的距离.
19. 如图,在三棱柱中,侧面底面,,,且,为中点.
(1)求证平面
(2)在上是否存在一点,使得平面,若不存在,说明理由;若存在,确定点E的位置.
20. 某公司在一次入职面试中,共设有3轮测试,每轮测试设有一道题目,面试者能正确回答两道题目的即可通过面试,累计答错两道题目的即被淘汰.已知李明能正确回答每一道题目的概率均为,且各轮题目能否正确回答互不影响.
(1)求李明不需要进入第三轮测试的概率;
(2)求李明通过面试的概率.
21. 如图,在棱长为1的正方体ABCD- A1B1C1D1中,E、F、G分别DD1、BD、BB1是中点.
(1)证明:EFCF;
(2)求EF与CG所成角的余弦值;
(3)求CE长.
22. 已知的三个内角A,B,C的对边分别为a,b,c,且
(1)若,判断的形状并说明理由;
(2)若是锐角三角形,求的取值范围.
23. 如图,已知长方形中,,,M为DC的中点.将沿折起,使得平面⊥平面.
(1)求证:;
(2)若点是线段上的一动点,问点在何位置时,二面角的余弦值为.
北大公学禹州国际学校2022-2023学年高二上学期9月开学考试
数学试题答案
一、单选题
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】C
【4题答案】
【答案】D
【5题答案】
【答案】B
【6题答案】
【答案】D
【7题答案】
【答案】A
【8题答案】
【答案】B
二、填空题
【9题答案】
【答案】3
【10题答案】
【答案】
【11题答案】
【答案】.
【12题答案】
【答案】
【13题答案】
【答案】
【14题答案】
【答案】a或2a
【15题答案】
【答案】##
【16题答案】
【答案】
三、解答题
【17题答案】
【答案】(1)证明略
(2)30°
【18题答案】
【答案】(1);
(2).
【19题答案】
【答案】(1)证明略
(2)存在,E为线段BC1中点
【20题答案】
【答案】(1)
(2)
【21题答案】
【答案】(1)证明略;
(2);
(3).
【22题答案】
【答案】(1)等边三角形,理由略;
(2)
【23题答案】
【答案】(1)略;(2)为中点.
数学试题
一、单选题
1. 在三棱锥中,,,,是边长为的等边三角形,点E为棱的中点,则三棱锥的体积为( )
A. B. C. D.
2. 如图,平面平面是等边三角形,四边形是矩形,且,E是的中点,F是上一点,当时,( )
A. 3 B. C. D. 2
3. 在下列条件中,一定能使空间中的四点共面的是( )
A. B.
C. D.
4. 如图,在大小为45°的二面角A EF D中,四边形ABFE,CDEF都是边长为1的正方形,则B,D两点间的距离是( )
A B.
C. 1 D.
5. 在中,角,,对边分别为,,,若,,则面积的最大值为( )
A. 1 B. C. 2 D.
6. 已知的内角所对的边分别为满足且,则( )
A. B. C. D.
7. 已知P为空间中任意一点,A、B、C、D四点满足任意三点均不共线,但四点共面,且,则实数x的值为( )
A. B. C. D.
8. 锐角中,若,则的取值范围是( )
A. B. C. D.
二、填空题
9. 已知空间向量,,,若,,共面,则______.
10. 在四面体ABCD中,,,,且,则几何体ABCD的外接球的体积为______.
11. 在三棱锥中,侧棱、、两两垂直,、、的面积分别为、、,则三棱锥的外接球的体积为__________.
12. 已知空间向量,,且与垂直,则等于 ___.
13. 已知点,,,若,,三点共线,则______.
14. 如图所示,在直三棱柱中,底面是以ABC为直角的等腰三角形,,,是的中点,点在棱上,要使平面,则___________.
15. 如图,等边三角形,是等腰三角形,交于 ,则__________.
16. 正方体中,分别是上底面和侧面的中心,若,则______
三、解答题
17. 如图,在正方体中,棱长为2,M、N分别为、AC的中点.
(1)证明:平面;
(2)求与平面所成角的大小.
18. 如图,在梯形ABCD中,,,,平面ABCD,且,点F在AD上,且.
(1)求点A到平面PCF的距离;
(2)求AD到平面PBC的距离.
19. 如图,在三棱柱中,侧面底面,,,且,为中点.
(1)求证平面
(2)在上是否存在一点,使得平面,若不存在,说明理由;若存在,确定点E的位置.
20. 某公司在一次入职面试中,共设有3轮测试,每轮测试设有一道题目,面试者能正确回答两道题目的即可通过面试,累计答错两道题目的即被淘汰.已知李明能正确回答每一道题目的概率均为,且各轮题目能否正确回答互不影响.
(1)求李明不需要进入第三轮测试的概率;
(2)求李明通过面试的概率.
21. 如图,在棱长为1的正方体ABCD- A1B1C1D1中,E、F、G分别DD1、BD、BB1是中点.
(1)证明:EFCF;
(2)求EF与CG所成角的余弦值;
(3)求CE长.
22. 已知的三个内角A,B,C的对边分别为a,b,c,且
(1)若,判断的形状并说明理由;
(2)若是锐角三角形,求的取值范围.
23. 如图,已知长方形中,,,M为DC的中点.将沿折起,使得平面⊥平面.
(1)求证:;
(2)若点是线段上的一动点,问点在何位置时,二面角的余弦值为.
北大公学禹州国际学校2022-2023学年高二上学期9月开学考试
数学试题答案
一、单选题
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】C
【4题答案】
【答案】D
【5题答案】
【答案】B
【6题答案】
【答案】D
【7题答案】
【答案】A
【8题答案】
【答案】B
二、填空题
【9题答案】
【答案】3
【10题答案】
【答案】
【11题答案】
【答案】.
【12题答案】
【答案】
【13题答案】
【答案】
【14题答案】
【答案】a或2a
【15题答案】
【答案】##
【16题答案】
【答案】
三、解答题
【17题答案】
【答案】(1)证明略
(2)30°
【18题答案】
【答案】(1);
(2).
【19题答案】
【答案】(1)证明略
(2)存在,E为线段BC1中点
【20题答案】
【答案】(1)
(2)
【21题答案】
【答案】(1)证明略;
(2);
(3).
【22题答案】
【答案】(1)等边三角形,理由略;
(2)
【23题答案】
【答案】(1)略;(2)为中点.
同课章节目录
