2022年秋青岛版数学七年级上册 第四章 数据的收集整理与描述 复习与测试(含解析)
文档属性
| 名称 | 2022年秋青岛版数学七年级上册 第四章 数据的收集整理与描述 复习与测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 11:40:17 | ||
图片预览


文档简介
第四章 复习与测试
一、单选题
1.小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
A.各项消费金额占消费总金额的百分比
B.各项消费的金额
C.消费的总金额
D.各项消费金额的增减变化情况
2.以下调查中,是用普查方式收集数据的为( )
①为了了解全校学生对任课教师的数学意见,学校向全校学生进行问卷调查;
②为了了解初中生上网情况,某市团委对所初中学校的部分学生进行调查;
③某班学生拟组织一次春游活动,为了确定春游的地点,向全班同学进行调查;
④为了了解全班同学的作业完成情况,对学号为奇数的学生进行调查.
A.①③ B.①② C.②④ D.②③
3.把过期的药品随意丢弃,会造成对土壤和水体的污染,危害人们的健康.如何处理过期药品,有关机构随机对若干家庭进行调查,调查结果如图,其中对过期药品处理不正确的家庭达到( )
A. B. C. D.
4.某校九(1)班的全体同学最喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
A.从图中可以直接看出喜欢各种球类的具体人数
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系
5.某校七年级共320名学生参加数学测试,随机抽取50名学生的成绩进行统计,其中15名学生成绩达到优秀,估计该校七年级学生在这次数学测试中达到优秀的人数大约有( )
A.50人 B.64人 C.90人 D.96人
6.为了了解我市参加中考的39 000名学生的视力情况,抽查了2 000名学生的视力进行统计分析,下面四个判断中,正确的是( )
A.39 000名学生是总体
B.每名学生是总体的一个个体
C.2 000名学生的视力情况是总体的一个样本
D.上述调查是普查
7.宾馆有100间相同的客房,经过一段时间的经营,发现客房定价与客房的入住率之间有下表所示的关系,按照这个关系,要使客房的收入最高,每间客房的定价应为( )
每间房价(元)
入住率
A.300元 B.280元 C.260元 D.220元
二、填空题
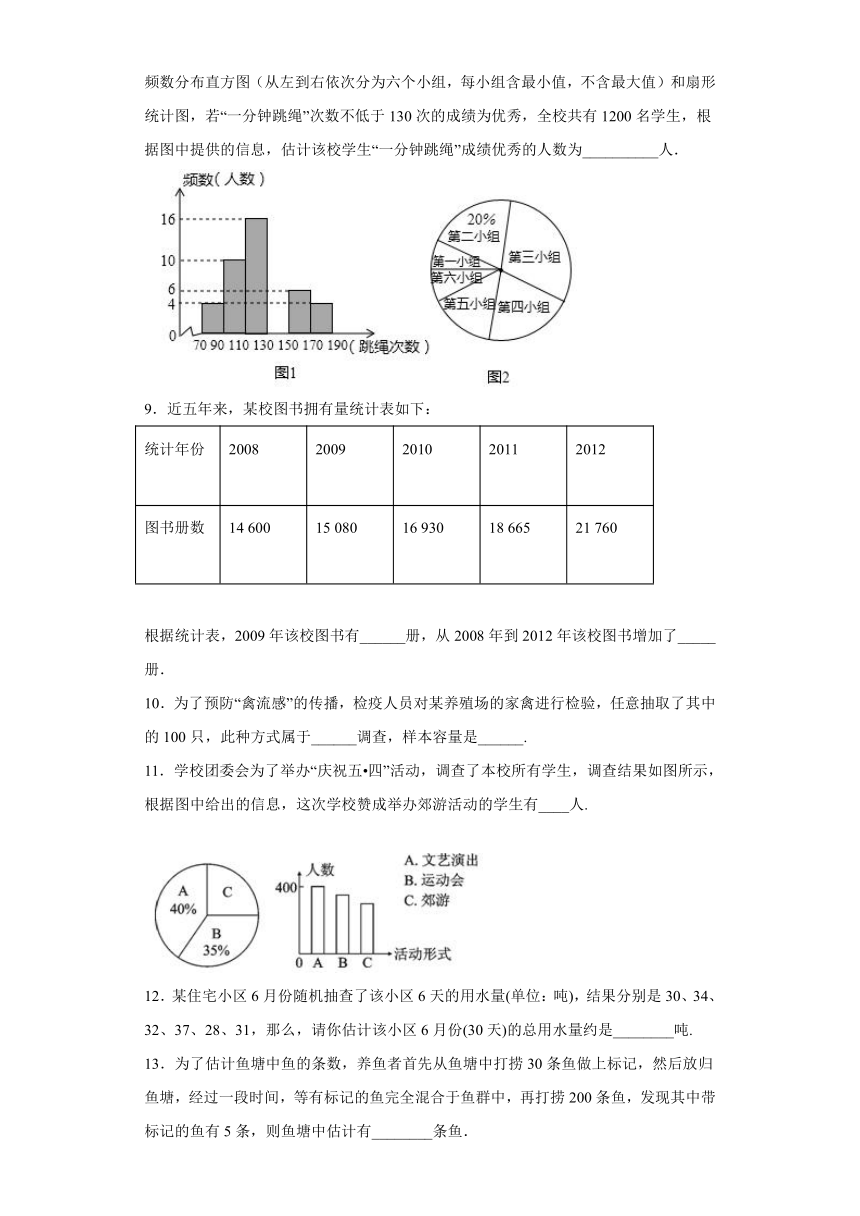
8.(2016福建省莆田市)在大课间活动中,同学们积极参加体育锻炼,小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,估计该校学生“一分钟跳绳”成绩优秀的人数为__________人.
9.近五年来,某校图书拥有量统计表如下:
统计年份 2008 2009 2010 2011 2012
图书册数 14 600 15 080 16 930 18 665 21 760
根据统计表,2009年该校图书有______册,从2008年到2012年该校图书增加了_____册.
10.为了预防“禽流感”的传播,检疫人员对某养殖场的家禽进行检验,任意抽取了其中的100只,此种方式属于______调查,样本容量是______.
11.学校团委会为了举办“庆祝五 四”活动,调查了本校所有学生,调查结果如图所示,根据图中给出的信息,这次学校赞成举办郊游活动的学生有____人.
12.某住宅小区6月份随机抽查了该小区6天的用水量(单位:吨),结果分别是30、34、32、37、28、31,那么,请你估计该小区6月份(30天)的总用水量约是________吨.
13.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有5条,则鱼塘中估计有________条鱼.
三、解答题
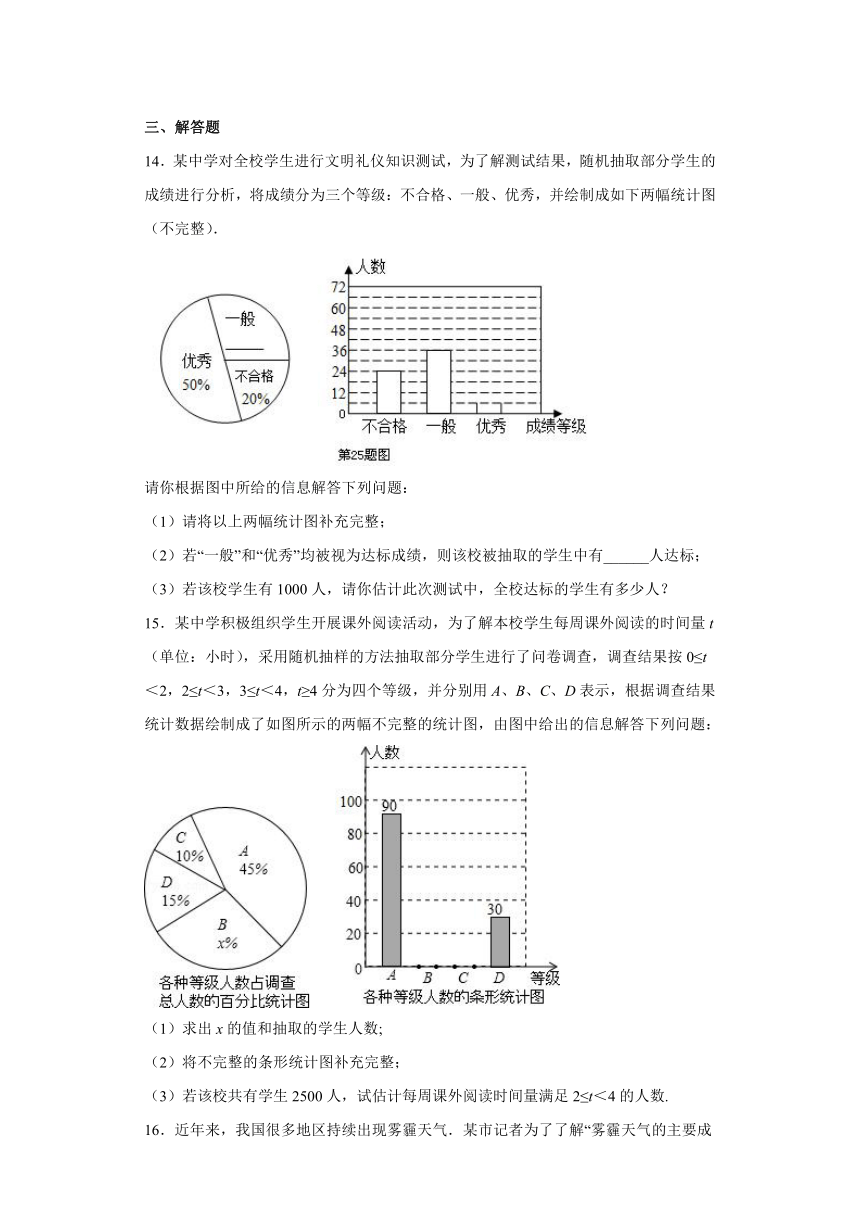
14.某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有______人达标;
(3)若该校学生有1000人,请你估计此次测试中,全校达标的学生有多少人?
15.某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
(1)求出x的值和抽取的学生人数;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数.
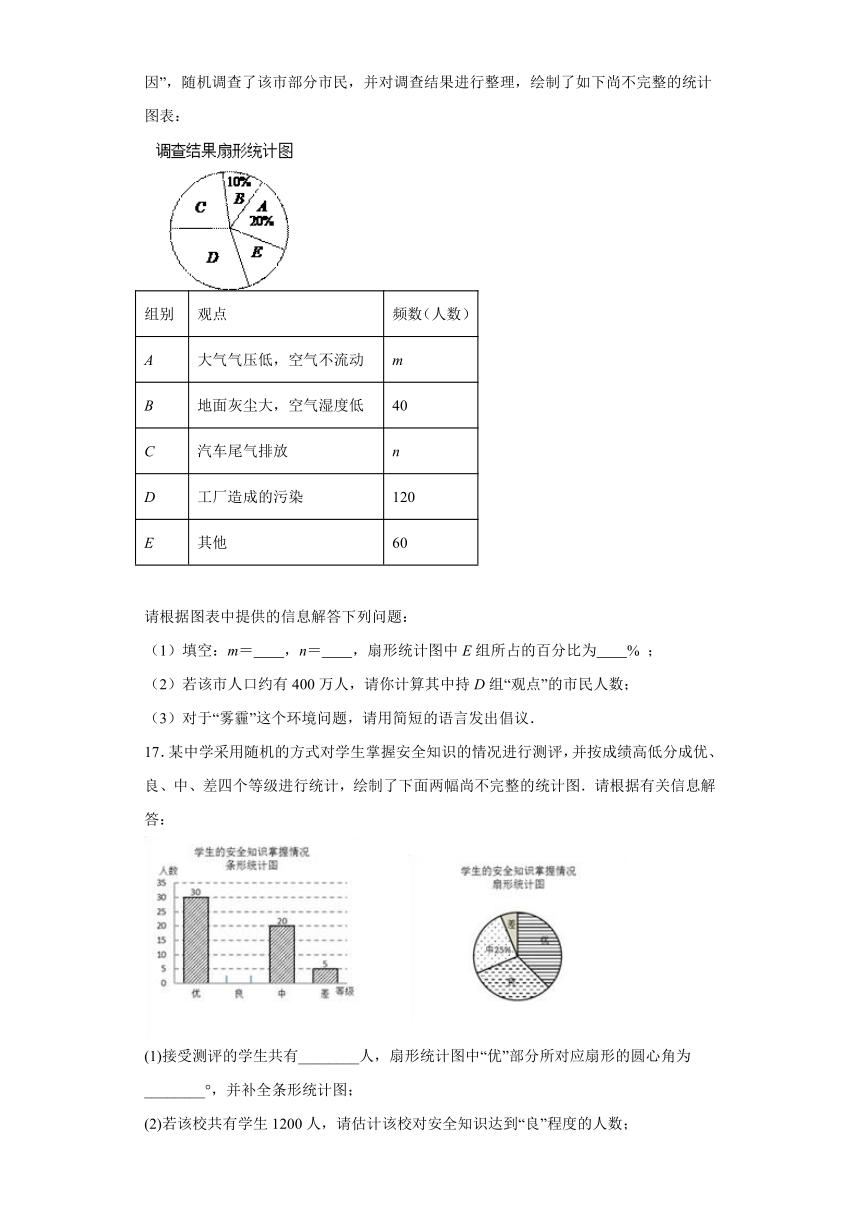
16.近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表:
组别 观点 频数(人数)
A 大气气压低,空气不流动 m
B 地面灰尘大,空气湿度低 40
C 汽车尾气排放 n
D 工厂造成的污染 120
E 其他 60
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 % ;
(2)若该市人口约有400万人,请你计算其中持D组“观点”的市民人数;
(3)对于“雾霾”这个环境问题,请用简短的语言发出倡议.
17.某中学采用随机的方式对学生掌握安全知识的情况进行测评,并按成绩高低分成优、良、中、差四个等级进行统计,绘制了下面两幅尚不完整的统计图.请根据有关信息解答:
(1)接受测评的学生共有________人,扇形统计图中“优”部分所对应扇形的圆心角为________°,并补全条形统计图;
(2)若该校共有学生1200人,请估计该校对安全知识达到“良”程度的人数;
(3)测评成绩前五名的学生恰好3个女生和2个男生,现从中随机抽取2人参加市安全知识竞赛,请用树状图或列表法求出抽到1个男生和1个女生的概率.
18.第三届世界互联网大会(3rd World Internet Conference),是由中华人民共和国倡导并举办的互联网盛会,于2016年11月16日至18日在浙江乌镇举办.某初中学校为了了解本校学生对本次互联网大会的关注程度(关注程度分为:A.特别关注;B.一般关注;C.偶尔关注;D.不关注),随机抽取了部分学生进行调查,并将结果绘制成频数折线统计图1和扇形统计图2(不完整)请根据图中信息回答问题.
(1)此次抽样调查中,共调查了多少名学生?
(2)求出图2中扇形B所对的圆心角度数,并将图1补充完整.
(3)在这次调查中,九(1)班共有甲、乙、丙、丁四人“特别关注”本届互联网大会,现准备从四人中随机抽取两人进行交流,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
19.某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数 质量等级 天数(天)
0﹣50 优 m
51﹣100 良 44
101﹣150 轻度污染 n
151﹣200 中度污染 4
201﹣300 重度污染 2
300以上 严重污染 2
(1 )统计表中m= ,n= .扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天?
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议.
20.为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.
(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
参考答案:
1.A【分析】读懂题意,从题意中得到必要的信息是解决问题的关键.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.因此,
【详解】解:从图中可以看出各项消费金额占消费总金额的百分比.
故选A.
2.A【分析】根据抽样调查和全面调查的特点依次分析各项即可判断.
【详解】①为了了解全校学生对任课教师的意见,学校向全校学生进行问卷调查,属于全面调查;
②为了了解初中生上网情况,某市团委对10所初中的部分学生进行调查,属于抽样调查;
③某班学生拟组织一次春游活动,为了确定春游的地点,向同学进行调查,属于全面调查;
④了解全班同学的作业完成情况,对学号为奇数的学生进行调查,属于抽样调查;
故选A.
【点睛】本题考查了抽样调查和全面调查. 抓住普查的特点是解题的关键.
3.D【详解】由图可知,只有封存家中等待处理的属于正确的处理方法,所以对过期药品处理不正确的家庭达到1-22%=78%,故选D.
4.D【分析】利用扇形统计图的特点,可以得到各类所占的比例,但总数不确定,不能确定每类的具体人数.
【详解】解:因为扇形统计图直接反映部分占总体的百分比大小,不能反映具体数量的多少和变化情况,所以A、B、C都错误.
故答案为:D
【点睛】考点:扇形统计图.
5.D【详解】随机抽取了50名学生的成绩进行统计,共有15名学生成绩达到优秀,
∴样本优秀率为:15÷50=30%,
又∵某校七年级共320名学生参加数学测试,
∴该校七年级学生在这次数学测试中达到优秀的人数为:320×30%=96人.
故选D.
6.C【详解】根据题意:A.39 000名学生的视力情况是总体,故本选项错误;
B.每名学生的视力情况是总体的一个个体,故本选项错误;
C.2 000名学生的视力情况是总体的一个样本,故本选项正确;
D.上述调查是抽样调查,故本选项错误.故选C.
7.C【详解】当每间客房的定价为300元时,客房的收入为100×65%×300=19500(元);
当每间客房的定价为280元时,客房的收入为100×75%×280=21000(元);
当每间客房的定价为260元时,客房的收入为100×85%×260=22100(元);
当每间客房的定价为220元时,客房的收入为100×95%×220=20900(元).
所以当每间客房的定价为260元时,客房的收入最高.故选C.
8.480.【详解】试题分析:总人数是:10÷20%=50(人),第四小组的人数是:50﹣4﹣10﹣16﹣6﹣4=10,所以该校九年级女生“一分钟跳绳”成绩为优秀的人数是:×1200=480,故答案为480.
考点:频数(率)分布直方图;用样本估计总体;扇形统计图.
9.15080,7160.【详解】2009年该校图书有15080册,从2008年到2012年该校图书增加了21760-14600=7160(册).
10. 抽样 100【详解】任意抽取了其中的100只,此种方式属于抽样调查,样本容量是100.
11.250【分析】由扇形统计图可知,赞成举办郊游的学生占1-40%-35%=25%,根据赞成举办文艺演出的人数与对应的百分比可求出总人数,由此即可解决.
【详解】400÷40%=1000(人),
1000×(1-40%-35%)=1000×25%=250(人),
故答案为250.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
12.960【详解】试题分析:要估计该小区6月份(30天)的总用水量,就要算出这六天的平均用水量,这个平均数可用样本平均数来代替,即求出6天用水的平均数即可.
解:(30+34+…+31)÷6=32,
∴估计该小区6月份(30天)的总用水量约是32×30=960吨.
故答案为960.
考点:算术平均数;用样本估计总体.
13.1200【详解】试题分析:先打捞200条鱼,发现其中带标记的鱼有5条,求出有标记的鱼占的百分比,再根据共有30条鱼做上标记,即可得出答案.
解:∵打捞200条鱼,发现其中带标记的鱼有5条,
∴有标记的鱼占×100%=2.5%,
∵共有30条鱼做上标记,
∴鱼塘中估计有30÷2.5%=1200(条).
故答案为1200.
考点:用样本估计总体.
14.详见解析.【详解】解:(1)成绩一般的学生占的百分比为1-20%-50%=30%
测试的学生总人数为24÷20%=120
成绩优秀的人数为120×50%=60
所补充图形如下所示:
(2)该校被抽取的学生中达标的人数为36+60=96.
(3)1200×(50%+30%)=960(人)
答:估计全校达标的学生有960人.
15.(1)30;200人;(2)作图见解析;(3)1000人.【详解】试题分析:(1)根据所有等级的百分比的和为1,则可计算出x的值;由条形图可知A等级有90人,由扇形图可知对应的百分比为45%,那么抽查的学生总数=A等级的人数÷对应的百分比,计算即可求解;
(2)再求出B级与C级的人数,即可作图;
(3)利用每周课外阅读时间量满足2≤t<4的人数=该校总人数×B级的与C级百分比的和计算即可.
试题解析:(1)∵x%+15%+10%+45%=1,
∴x=30;
调查的总人数=90÷45%=200(人)
(2)B等级人数=200×30%=60(人);C等级人数=200×10%=20(人),
(3)2500×(10%+30%)=1000(人),
所以估计每周课外阅读时间量满足2≤t<4的人数为1000人
【点睛】本题主要考查了条形统计图,扇形统计图及用样本估计总体.解题的关键是读懂统计图,能从条形统计图,扇形统计图中得到准确的信息.
16.(1)80, 100,15; (2)120万人;(3)答案见解析【详解】试题分析:(1)根据B组频数及其所占百分比求得样本容量,再根据频数=总数×频率及各组频数之和等于总数,解答即可;
(2)用总人数乘以样本中D观点所占百分比即可得;
(3)根据各种观点所占百分比,有针对的提出合理的改善意见即可;
试题解析:
(1)根据题意,本次调查的总人数为40÷10%=400(人),
∴m=400×20%=80,n=400-(80+40+120+60)=100,
则扇形统计图中E组所占的百分比为
(2)400×=120(万),
答:其中持D组“观点”的市民人数约为120万人;
(3)根据所抽取样本中持C、D两种观点的人数占总人数的比例较大,
所以倡议今后的环境改善中严格控制工厂的污染排放,同时市民多乘坐公共汽车,
减少私家车出行的次数.
17.(1)80,135°,条形统计图见解析;(2)825人;(3)图表见解析,(抽到1男1女). 【详解】试题分析:(1)、根据“中”的人数和百分比得出总人数,然后求出优所占的百分比,得出圆心角的度数;(2)、根据题意得出“良”和“优”两种所占的百分比,从而得出全校的总数;(3)、根据题意利用列表法或者树状图法画出所有可能出现的情况,然后根据概率的计算法则求出概率.
试题解析:(1)80,135°; 条形统计图如图所示
(2)该校对安全知识达到“良”程度的人数:(人)
(3)解法一:列表如下:
所有等可能的结果为20种,其中抽到一男一女的为12种,
所以(抽到1男1女).
女1 女2 女3 男1 男2
女1 --- 女2女1 女3女1 男1女1 男2女1
女2 女1女2 --- 女3女2 男1女2 男2女2
女3 女1女3 女2女3 --- 男1女3 男2女3
男1 女1男1 女2男1 女3男1 --- 男2男1
男2 女1男2 女2男2 女3男2 男1男2 ---
解法二:画树状图如下:
所有等可能的结果为20种,其中抽到一男一女的为12种,
所以(抽到1男1女).
18.(1)250; (2)108 图1补充见解析;(3)列表或树状图见解析,P(抽取甲乙)=.【详解】试题分析:(1)根据题意,用偶尔关注的人数除以偶尔关注的比例即可求解;
(2)由扇形统计图即可求出扇形B所对的圆心角度数,然后再计算A、B的人数,补全图形即可;
(3)列表或画树状图得出所有等可能的情况数,找出恰好是甲与乙的情况,即可确定出所求概率.
试题解析:(1)100÷40%=250
∴共调查了250名学生.
(2)1-20%-10%-40%=30%
360°×30%=108°
∴扇形B所对的圆心角度数是108
250×10%=25;
250×30%=75
补图如下:
(3)列表如下(或树状图):
共有12种等可能的结果数,其中含甲和乙的结果数为2,
所以九(1)班抽取的两人恰好是甲和乙的概率.
P(抽取甲乙)==.
19.(1)20,8,55;(2)答案见解析;292天;(3)答案见解析【分析】(1)由A占25%,即可求得m的值,继而求得n的值,然后求得空气质量等级为“良”的天数占的百分比;(2)首先由(1)补全统计图,然后利用样本估计总体的知识求解即可求得答案;(3)提出合理建议,比如不燃放烟花爆竹或少燃放烟花爆竹等.
【详解】解:(1)∵m=80×25%=20,n=80﹣20﹣44﹣4﹣2﹣2=8,
∴空气质量等级为“良”的天数占:×100%=55%.
故答案为20,8,55;
(2)估计该市城区全年空气质量等级为“优”和“良”的天数共:365×(25%+55%)=292(天),
答:估计该市城区全年空气质量等级为“优”和“良”的天数共292天;
补全统计图:
(3)建议不要燃放烟花爆竹.
20.(1)、48;(2)、90°;(3)、300.【详解】(1)因为12+16+6+10+4=48
所以在这次调查中,一共抽查了48名学生.
(2)由条形图可求出参加“音乐活动”项目的人数所占抽查总人数的百分比为.
所以参加“音乐活动”项目对扇形的圆心角的度数为360.
(3)2 400×=300(人).
答:该校参加“美术活动”项目的人数约为300人.
一、单选题
1.小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
A.各项消费金额占消费总金额的百分比
B.各项消费的金额
C.消费的总金额
D.各项消费金额的增减变化情况
2.以下调查中,是用普查方式收集数据的为( )
①为了了解全校学生对任课教师的数学意见,学校向全校学生进行问卷调查;
②为了了解初中生上网情况,某市团委对所初中学校的部分学生进行调查;
③某班学生拟组织一次春游活动,为了确定春游的地点,向全班同学进行调查;
④为了了解全班同学的作业完成情况,对学号为奇数的学生进行调查.
A.①③ B.①② C.②④ D.②③
3.把过期的药品随意丢弃,会造成对土壤和水体的污染,危害人们的健康.如何处理过期药品,有关机构随机对若干家庭进行调查,调查结果如图,其中对过期药品处理不正确的家庭达到( )
A. B. C. D.
4.某校九(1)班的全体同学最喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
A.从图中可以直接看出喜欢各种球类的具体人数
B.从图中可以直接看出全班的总人数
C.从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况
D.从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系
5.某校七年级共320名学生参加数学测试,随机抽取50名学生的成绩进行统计,其中15名学生成绩达到优秀,估计该校七年级学生在这次数学测试中达到优秀的人数大约有( )
A.50人 B.64人 C.90人 D.96人
6.为了了解我市参加中考的39 000名学生的视力情况,抽查了2 000名学生的视力进行统计分析,下面四个判断中,正确的是( )
A.39 000名学生是总体
B.每名学生是总体的一个个体
C.2 000名学生的视力情况是总体的一个样本
D.上述调查是普查
7.宾馆有100间相同的客房,经过一段时间的经营,发现客房定价与客房的入住率之间有下表所示的关系,按照这个关系,要使客房的收入最高,每间客房的定价应为( )
每间房价(元)
入住率
A.300元 B.280元 C.260元 D.220元
二、填空题
8.(2016福建省莆田市)在大课间活动中,同学们积极参加体育锻炼,小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,估计该校学生“一分钟跳绳”成绩优秀的人数为__________人.
9.近五年来,某校图书拥有量统计表如下:
统计年份 2008 2009 2010 2011 2012
图书册数 14 600 15 080 16 930 18 665 21 760
根据统计表,2009年该校图书有______册,从2008年到2012年该校图书增加了_____册.
10.为了预防“禽流感”的传播,检疫人员对某养殖场的家禽进行检验,任意抽取了其中的100只,此种方式属于______调查,样本容量是______.
11.学校团委会为了举办“庆祝五 四”活动,调查了本校所有学生,调查结果如图所示,根据图中给出的信息,这次学校赞成举办郊游活动的学生有____人.
12.某住宅小区6月份随机抽查了该小区6天的用水量(单位:吨),结果分别是30、34、32、37、28、31,那么,请你估计该小区6月份(30天)的总用水量约是________吨.
13.为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放归鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞200条鱼,发现其中带标记的鱼有5条,则鱼塘中估计有________条鱼.
三、解答题
14.某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有______人达标;
(3)若该校学生有1000人,请你估计此次测试中,全校达标的学生有多少人?
15.某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
(1)求出x的值和抽取的学生人数;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数.
16.近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表:
组别 观点 频数(人数)
A 大气气压低,空气不流动 m
B 地面灰尘大,空气湿度低 40
C 汽车尾气排放 n
D 工厂造成的污染 120
E 其他 60
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为 % ;
(2)若该市人口约有400万人,请你计算其中持D组“观点”的市民人数;
(3)对于“雾霾”这个环境问题,请用简短的语言发出倡议.
17.某中学采用随机的方式对学生掌握安全知识的情况进行测评,并按成绩高低分成优、良、中、差四个等级进行统计,绘制了下面两幅尚不完整的统计图.请根据有关信息解答:
(1)接受测评的学生共有________人,扇形统计图中“优”部分所对应扇形的圆心角为________°,并补全条形统计图;
(2)若该校共有学生1200人,请估计该校对安全知识达到“良”程度的人数;
(3)测评成绩前五名的学生恰好3个女生和2个男生,现从中随机抽取2人参加市安全知识竞赛,请用树状图或列表法求出抽到1个男生和1个女生的概率.
18.第三届世界互联网大会(3rd World Internet Conference),是由中华人民共和国倡导并举办的互联网盛会,于2016年11月16日至18日在浙江乌镇举办.某初中学校为了了解本校学生对本次互联网大会的关注程度(关注程度分为:A.特别关注;B.一般关注;C.偶尔关注;D.不关注),随机抽取了部分学生进行调查,并将结果绘制成频数折线统计图1和扇形统计图2(不完整)请根据图中信息回答问题.
(1)此次抽样调查中,共调查了多少名学生?
(2)求出图2中扇形B所对的圆心角度数,并将图1补充完整.
(3)在这次调查中,九(1)班共有甲、乙、丙、丁四人“特别关注”本届互联网大会,现准备从四人中随机抽取两人进行交流,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
19.某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数 质量等级 天数(天)
0﹣50 优 m
51﹣100 良 44
101﹣150 轻度污染 n
151﹣200 中度污染 4
201﹣300 重度污染 2
300以上 严重污染 2
(1 )统计表中m= ,n= .扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天?
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议.
20.为了解某学校学生的个性特长发展情况,在全校范围内随机抽查了部分学生参加音乐、体育、美术、书法等活动项目(每人只限一项)的情况.并将所得数据进行了统计,结果如图所示.
(1)求在这次调查中,一共抽查了多少名学生;
(2)求出扇形统计图中参加“音乐”活动项目所对扇形的圆心角的度数;
(3)若该校有2400名学生,请估计该校参加“美术”活动项目的人数
参考答案:
1.A【分析】读懂题意,从题意中得到必要的信息是解决问题的关键.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.因此,
【详解】解:从图中可以看出各项消费金额占消费总金额的百分比.
故选A.
2.A【分析】根据抽样调查和全面调查的特点依次分析各项即可判断.
【详解】①为了了解全校学生对任课教师的意见,学校向全校学生进行问卷调查,属于全面调查;
②为了了解初中生上网情况,某市团委对10所初中的部分学生进行调查,属于抽样调查;
③某班学生拟组织一次春游活动,为了确定春游的地点,向同学进行调查,属于全面调查;
④了解全班同学的作业完成情况,对学号为奇数的学生进行调查,属于抽样调查;
故选A.
【点睛】本题考查了抽样调查和全面调查. 抓住普查的特点是解题的关键.
3.D【详解】由图可知,只有封存家中等待处理的属于正确的处理方法,所以对过期药品处理不正确的家庭达到1-22%=78%,故选D.
4.D【分析】利用扇形统计图的特点,可以得到各类所占的比例,但总数不确定,不能确定每类的具体人数.
【详解】解:因为扇形统计图直接反映部分占总体的百分比大小,不能反映具体数量的多少和变化情况,所以A、B、C都错误.
故答案为:D
【点睛】考点:扇形统计图.
5.D【详解】随机抽取了50名学生的成绩进行统计,共有15名学生成绩达到优秀,
∴样本优秀率为:15÷50=30%,
又∵某校七年级共320名学生参加数学测试,
∴该校七年级学生在这次数学测试中达到优秀的人数为:320×30%=96人.
故选D.
6.C【详解】根据题意:A.39 000名学生的视力情况是总体,故本选项错误;
B.每名学生的视力情况是总体的一个个体,故本选项错误;
C.2 000名学生的视力情况是总体的一个样本,故本选项正确;
D.上述调查是抽样调查,故本选项错误.故选C.
7.C【详解】当每间客房的定价为300元时,客房的收入为100×65%×300=19500(元);
当每间客房的定价为280元时,客房的收入为100×75%×280=21000(元);
当每间客房的定价为260元时,客房的收入为100×85%×260=22100(元);
当每间客房的定价为220元时,客房的收入为100×95%×220=20900(元).
所以当每间客房的定价为260元时,客房的收入最高.故选C.
8.480.【详解】试题分析:总人数是:10÷20%=50(人),第四小组的人数是:50﹣4﹣10﹣16﹣6﹣4=10,所以该校九年级女生“一分钟跳绳”成绩为优秀的人数是:×1200=480,故答案为480.
考点:频数(率)分布直方图;用样本估计总体;扇形统计图.
9.15080,7160.【详解】2009年该校图书有15080册,从2008年到2012年该校图书增加了21760-14600=7160(册).
10. 抽样 100【详解】任意抽取了其中的100只,此种方式属于抽样调查,样本容量是100.
11.250【分析】由扇形统计图可知,赞成举办郊游的学生占1-40%-35%=25%,根据赞成举办文艺演出的人数与对应的百分比可求出总人数,由此即可解决.
【详解】400÷40%=1000(人),
1000×(1-40%-35%)=1000×25%=250(人),
故答案为250.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
12.960【详解】试题分析:要估计该小区6月份(30天)的总用水量,就要算出这六天的平均用水量,这个平均数可用样本平均数来代替,即求出6天用水的平均数即可.
解:(30+34+…+31)÷6=32,
∴估计该小区6月份(30天)的总用水量约是32×30=960吨.
故答案为960.
考点:算术平均数;用样本估计总体.
13.1200【详解】试题分析:先打捞200条鱼,发现其中带标记的鱼有5条,求出有标记的鱼占的百分比,再根据共有30条鱼做上标记,即可得出答案.
解:∵打捞200条鱼,发现其中带标记的鱼有5条,
∴有标记的鱼占×100%=2.5%,
∵共有30条鱼做上标记,
∴鱼塘中估计有30÷2.5%=1200(条).
故答案为1200.
考点:用样本估计总体.
14.详见解析.【详解】解:(1)成绩一般的学生占的百分比为1-20%-50%=30%
测试的学生总人数为24÷20%=120
成绩优秀的人数为120×50%=60
所补充图形如下所示:
(2)该校被抽取的学生中达标的人数为36+60=96.
(3)1200×(50%+30%)=960(人)
答:估计全校达标的学生有960人.
15.(1)30;200人;(2)作图见解析;(3)1000人.【详解】试题分析:(1)根据所有等级的百分比的和为1,则可计算出x的值;由条形图可知A等级有90人,由扇形图可知对应的百分比为45%,那么抽查的学生总数=A等级的人数÷对应的百分比,计算即可求解;
(2)再求出B级与C级的人数,即可作图;
(3)利用每周课外阅读时间量满足2≤t<4的人数=该校总人数×B级的与C级百分比的和计算即可.
试题解析:(1)∵x%+15%+10%+45%=1,
∴x=30;
调查的总人数=90÷45%=200(人)
(2)B等级人数=200×30%=60(人);C等级人数=200×10%=20(人),
(3)2500×(10%+30%)=1000(人),
所以估计每周课外阅读时间量满足2≤t<4的人数为1000人
【点睛】本题主要考查了条形统计图,扇形统计图及用样本估计总体.解题的关键是读懂统计图,能从条形统计图,扇形统计图中得到准确的信息.
16.(1)80, 100,15; (2)120万人;(3)答案见解析【详解】试题分析:(1)根据B组频数及其所占百分比求得样本容量,再根据频数=总数×频率及各组频数之和等于总数,解答即可;
(2)用总人数乘以样本中D观点所占百分比即可得;
(3)根据各种观点所占百分比,有针对的提出合理的改善意见即可;
试题解析:
(1)根据题意,本次调查的总人数为40÷10%=400(人),
∴m=400×20%=80,n=400-(80+40+120+60)=100,
则扇形统计图中E组所占的百分比为
(2)400×=120(万),
答:其中持D组“观点”的市民人数约为120万人;
(3)根据所抽取样本中持C、D两种观点的人数占总人数的比例较大,
所以倡议今后的环境改善中严格控制工厂的污染排放,同时市民多乘坐公共汽车,
减少私家车出行的次数.
17.(1)80,135°,条形统计图见解析;(2)825人;(3)图表见解析,(抽到1男1女). 【详解】试题分析:(1)、根据“中”的人数和百分比得出总人数,然后求出优所占的百分比,得出圆心角的度数;(2)、根据题意得出“良”和“优”两种所占的百分比,从而得出全校的总数;(3)、根据题意利用列表法或者树状图法画出所有可能出现的情况,然后根据概率的计算法则求出概率.
试题解析:(1)80,135°; 条形统计图如图所示
(2)该校对安全知识达到“良”程度的人数:(人)
(3)解法一:列表如下:
所有等可能的结果为20种,其中抽到一男一女的为12种,
所以(抽到1男1女).
女1 女2 女3 男1 男2
女1 --- 女2女1 女3女1 男1女1 男2女1
女2 女1女2 --- 女3女2 男1女2 男2女2
女3 女1女3 女2女3 --- 男1女3 男2女3
男1 女1男1 女2男1 女3男1 --- 男2男1
男2 女1男2 女2男2 女3男2 男1男2 ---
解法二:画树状图如下:
所有等可能的结果为20种,其中抽到一男一女的为12种,
所以(抽到1男1女).
18.(1)250; (2)108 图1补充见解析;(3)列表或树状图见解析,P(抽取甲乙)=.【详解】试题分析:(1)根据题意,用偶尔关注的人数除以偶尔关注的比例即可求解;
(2)由扇形统计图即可求出扇形B所对的圆心角度数,然后再计算A、B的人数,补全图形即可;
(3)列表或画树状图得出所有等可能的情况数,找出恰好是甲与乙的情况,即可确定出所求概率.
试题解析:(1)100÷40%=250
∴共调查了250名学生.
(2)1-20%-10%-40%=30%
360°×30%=108°
∴扇形B所对的圆心角度数是108
250×10%=25;
250×30%=75
补图如下:
(3)列表如下(或树状图):
共有12种等可能的结果数,其中含甲和乙的结果数为2,
所以九(1)班抽取的两人恰好是甲和乙的概率.
P(抽取甲乙)==.
19.(1)20,8,55;(2)答案见解析;292天;(3)答案见解析【分析】(1)由A占25%,即可求得m的值,继而求得n的值,然后求得空气质量等级为“良”的天数占的百分比;(2)首先由(1)补全统计图,然后利用样本估计总体的知识求解即可求得答案;(3)提出合理建议,比如不燃放烟花爆竹或少燃放烟花爆竹等.
【详解】解:(1)∵m=80×25%=20,n=80﹣20﹣44﹣4﹣2﹣2=8,
∴空气质量等级为“良”的天数占:×100%=55%.
故答案为20,8,55;
(2)估计该市城区全年空气质量等级为“优”和“良”的天数共:365×(25%+55%)=292(天),
答:估计该市城区全年空气质量等级为“优”和“良”的天数共292天;
补全统计图:
(3)建议不要燃放烟花爆竹.
20.(1)、48;(2)、90°;(3)、300.【详解】(1)因为12+16+6+10+4=48
所以在这次调查中,一共抽查了48名学生.
(2)由条形图可求出参加“音乐活动”项目的人数所占抽查总人数的百分比为.
所以参加“音乐活动”项目对扇形的圆心角的度数为360.
(3)2 400×=300(人).
答:该校参加“美术活动”项目的人数约为300人.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
