2022年秋数学青岛版七年级上册 第四章数据的收集整理与描述 复习与测试(含解析)
文档属性
| 名称 | 2022年秋数学青岛版七年级上册 第四章数据的收集整理与描述 复习与测试(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 318.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览



文档简介
第四章 复习与测试
一、单选题
1.一名同学调查了全班名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
最喜欢的节目类别 划记 人数 百分数(%)
相声 正
小品 正正正一
歌曲 正正
舞蹈 正一
其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )A.相声 B.小品 C.歌曲 D.舞蹈
2.如图,一个正在绘制的扇形统计图,整个圆表示某班参加体育活动的总人数,那么表示参加实心球训练的人数占总人数的的扇形是( )
A. B. C. D.
3.要了解一批电视机的使用寿命,从中任意抽取台电视机进行试验,在这个问题中,40是( )
A.个体 B.总体 C.样本容量 D.总体的一个样本
4.我市某中学为了了解年度下学期七年级数学学科期中考试分数段成绩的分布情况,从全校七年级名学生中抽取了名学生的期中数学成绩进行调查,在这次调查中,样本是( )
A.名学生 B.名学生的期中数学成绩
C.名学生 D.名学生的期中数学成绩
5.某市有5500名学生参加考试,为了了解考试情况,从中抽取1000名学生的成绩进行统计分析,在这个问题中,有下列三种说法:①1000名考生是总体的一个样本;②5500名考生是总体;③样本容量是1000.其中正确的说法有( )
A.0种 B.1种 C.2种 D.3种
6.老师对某班全体学生在电脑培训前后进行了一次水平测试,考分以同一标准划分为“不合格”、“合格”、“优秀”三个等级,成绩见下表.下列说法错误的是( )
A.培训前“不合格”的学生占80%
B.培训前成绩“合格”的学生是“优秀”学生的4倍
C.培训后80%的学生成绩达到了“合格”以上
D.培训后优秀率提高了30%
7.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( )
A.2013年昆明市九年级学生是总体 B.每一名九年级学生是个体
C.1000名九年级学生是总体的一个样本 D.样本容量是1000
8.(2016山东省泰安市)某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
9.(2016山东省泰安市)某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
10.某校公布了该校反映各年级学生体育达标情况的两张统计图(如图),该校七、八、九三个年级共有学生800人.甲、乙、丙三个同学看了这两张统计图后,甲说:“七年级的体育达标率最高.”乙说:“八年级共有学生264人.”丙说:“九年级的体育达标率最高.”甲、乙、丙三个同学中,说法正确的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.甲、乙和丙
二、填空题
11.妈妈做了一份美味可口的菜品,为了了解菜品的咸淡是否适合,于是妈妈取了一点品尝,这应该属于___________(填普查或抽样调查)
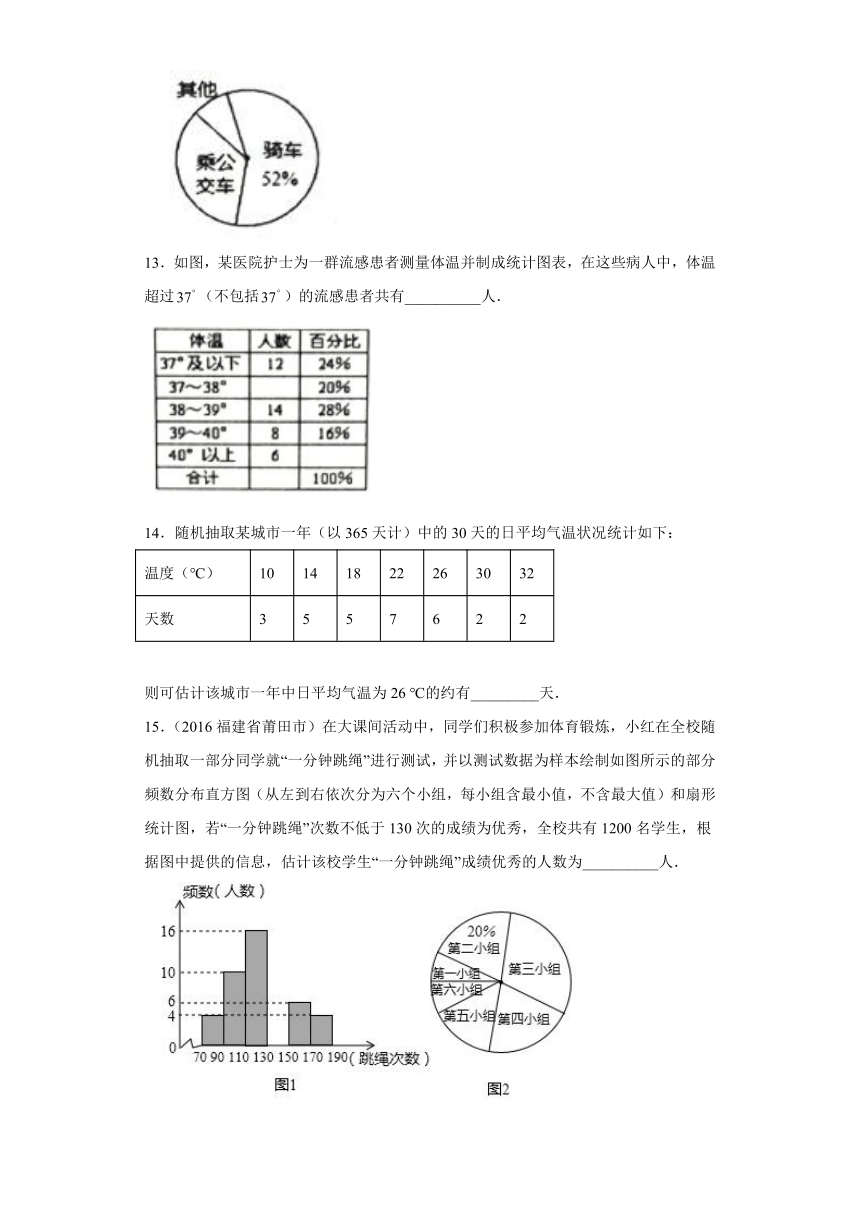
12.某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有人,乘坐公交车上学学生对应的扇形所占的圆心角的度数,则乘公交车上学的学生人数为__________.
13.如图,某医院护士为一群流感患者测量体温并制成统计图表,在这些病人中,体温超过(不包括)的流感患者共有__________人.
14.随机抽取某城市一年(以365天计)中的30天的日平均气温状况统计如下:
温度(℃) 10 14 18 22 26 30 32
天数 3 5 5 7 6 2 2
则可估计该城市一年中日平均气温为26 ℃的约有_________天.
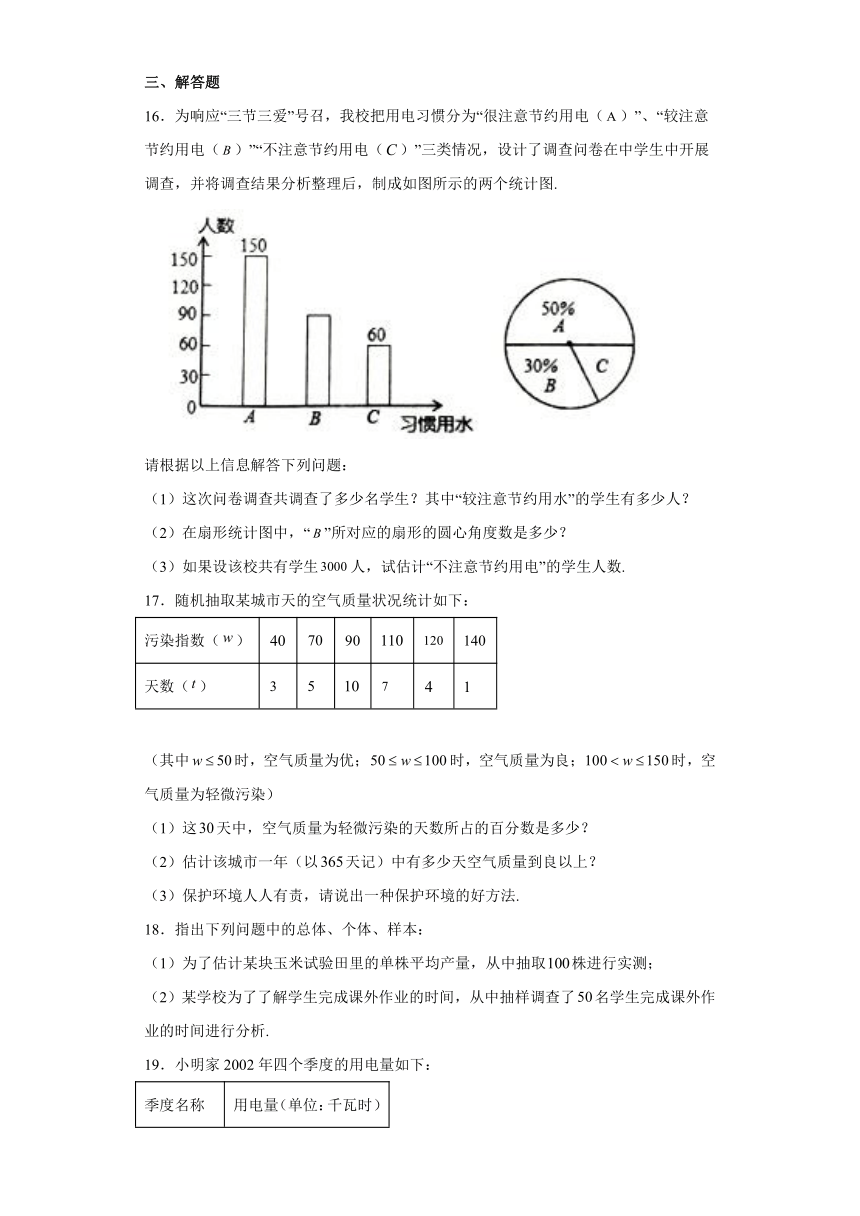
15.(2016福建省莆田市)在大课间活动中,同学们积极参加体育锻炼,小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,估计该校学生“一分钟跳绳”成绩优秀的人数为__________人.
三、解答题
16.为响应“三节三爱”号召,我校把用电习惯分为“很注意节约用电()”、“较注意节约用电()”“不注意节约用电()”三类情况,设计了调查问卷在中学生中开展调查,并将调查结果分析整理后,制成如图所示的两个统计图.
请根据以上信息解答下列问题:
(1)这次问卷调查共调查了多少名学生?其中“较注意节约用水”的学生有多少人?
(2)在扇形统计图中,“”所对应的扇形的圆心角度数是多少?
(3)如果设该校共有学生人,试估计“不注意节约用电”的学生人数.
17.随机抽取某城市天的空气质量状况统计如下:
污染指数()
天数()
(其中时,空气质量为优;时,空气质量为良;时,空气质量为轻微污染)
(1)这天中,空气质量为轻微污染的天数所占的百分数是多少?
(2)估计该城市一年(以天记)中有多少天空气质量到良以上?
(3)保护环境人人有责,请说出一种保护环境的好方法.
18.指出下列问题中的总体、个体、样本:
(1)为了估计某块玉米试验田里的单株平均产量,从中抽取株进行实测;
(2)某学校为了了解学生完成课外作业的时间,从中抽样调查了名学生完成课外作业的时间进行分析.
19.小明家2002年四个季度的用电量如下:
季度名称 用电量(单位:千瓦时)
第一季度 250
第二季度 150
第三季度 400
第四季度 200
其中各种电器用电量如下表:
各种电器 用电量(单位:千瓦时)
空调 250
冰箱 400
照明 100
彩电 150
其他 100
小明根据上面的数据制成下面的统计图.
根据以上三幅统计图回答:
(1)从哪幅统计图中可以看出各个季度用电量变化情况?
(2)从哪幅统计图中可以看出冰箱用电量超过总用电量的?
(3)从哪幅统计图中可以清楚地看出空调的用电量?
20.果园里有果树200棵,从中随机抽取5棵,每棵果树的产量如下(单位:kg):98,102,97,103,105,这5棵果树的平均产量为________kg,估计这200棵果树的总产量为________kg.
参考答案:
1.D【分析】此题只需根据划记的人数除以总人数,正确计算百分比,即可进行分析判断.
【详解】由统计表可得:
A. 相声划记应为5人,则百分数应为 ×100%=10%,故错误;
B. 小品划记应为16人,则百分数应为×100%=32%,故错误;
C. 歌曲划记为应10人,则百分数则百分数应为×100%=20%,故错误;
D. 舞蹈的划记为6人是正确的,百分数为×100%=12%,百分数也正确,故正确.
故选D.
【点睛】本题主要考查了统计表,较为简单.
2.D【分析】首先根据扇形G的圆心角为90°可得参加此训练的人数占总数的25%,再根据35%>25%,可得扇形的面积一定比G大,根据图可选出答案.
【详解】∵扇形G的圆心角为90°,
∴表示参加此训练的人数占总数的:90°÷360°×100%=25%,
∵35%>25%,
∴扇形的面积一定比G大,
∴表示参加实心球训练的人数占总人数的35%的扇形是H,
故选D.
【点睛】本题主要考查了扇形统计图.
3.C【分析】首先找出考查的对象是电视机的使用寿命,从中任意抽取40台电视机,40是指抽取的样本的个数,即样本容量.
【详解】本题中任意抽取的40台电视机是样本,对于其中的40,只是样本中个体的数目,所以是样本容量.故选C.
【点睛】本题主要考查了样本容量的概念,注意样本和样本容量的区别.
4.D【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,据此即可判断.
【详解】在这次调查中,样本是:200名学生的期末数学成绩;
故选D.
【点睛】本题主要考查了样本的概念,牢牢掌握样本的概念是解答本题的关键.
5.B【分析】根据总体:我们把所要考察的对象的全体叫做总体;个体:把组成总体的每一个考察对象叫做个体;样本:从总体中取出的一部分个体叫做这个总体的一个样本;样本容量:一个样本包括的个体数量叫做样本容量分别进行分析即可.
【详解】解:抽取的1000名学生的成绩是一个样本,故①错误;
5500名考生的考试成绩是总体,故②错误;
因为从中抽取1000名学生的成绩,所以样本容量是1000,故③正确.
故选B.
【点睛】此题主要考查了总体、个体、样本、样本容量,关键是掌握各个量的定义.
6.D【分析】此题只需根据统计表分别计算要求的数据,即可进行正确判断.
【详解】解:A、 =80%,故正确;
B、“优秀”学生为2人,所以培训前成绩“合格”的学生是“优秀”学生的4倍,故正确;
C、×100%=80%,故正确;
D、培训后优秀率:×100%=30%,培训前优秀率:×100%=4%,30%-4%=26%,所以培训后优秀率提高了26%,故错误.
故选D.
【点睛】本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
7.D【分析】根据总体、个体、样本、样本容量的概念结合选项选出正确答案即可.
【详解】A、2013年昆明市九年级学生的数学成绩是总体,原说法错误,故本选项不符合题意;
B、每一名九年级学生的数学成绩是个体,原说法错误,故本选项不符合题意;
C、1000名九年级学生的数学成绩是总体的一个样本,原说法错误,故本选项不符合题意;
D、样本容量是1000,该说法正确,故本选项符合题意.
故选:D.
8.D【分析】通过计算得出选项A、B、C正确,选项D错误,即可得出结论.
【详解】解:被调查的学生人数为60÷15%=400(人),∴选项A正确;
扇形统计图中D的圆心角为×360°=90°,∵×360°=36°,
360°(17.5%+15%+12.5%)=162°,
∴扇形统计图中E的圆心角=360°﹣162°﹣90°﹣36°=72°,
∴选项B正确;
∵400×=80(人),400×17.5%=70(人),∴选项C正确;
∵12.5%>10%, ∴喜欢选修课A的人数最少,∴选项D错误;
9.D【分析】通过计算得出选项A、B、C正确,选项D错误,即可得出结论.
【详解】解:被调查的学生人数为60÷15%=400(人),∴选项A正确;
扇形统计图中D的圆心角为×360°=90°,∵×360°=36°,
360°(17.5%+15%+12.5%)=162°,
∴扇形统计图中E的圆心角=360°﹣162°﹣90°﹣36°=72°,
∴选项B正确;
∵400×=80(人),400×17.5%=70(人),∴选项C正确;
∵12.5%>10%, ∴喜欢选修课A的人数最少,∴选项D错误;
10.B【详解】试题分析:由扇形统计图可以看出:八年级共有学生800×33%=264人;
七年级的达标率为;
九年级的达标率为;
八年级的达标率为.
则九年级的达标率最高.则乙、丙的说法是正确的,
故选B.
考点:1.扇形统计图;2.条形统计图.
11.抽样调查【分析】根据普查和抽样调查的定义,显然此题属于抽样调查.
【详解】由于只是取了一点品尝,所以应该是抽样调查.
故答案为:抽样调查.
【点睛】此题考查抽样调查和全面调查,解题关键在于掌握选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查,事关重大的调查往往选用普查.
12.20人【分析】先根据骑自行车上学的学生有26人占52%,求出总人数,再根据乘车部分所对应的圆心角的度数即可求出答案;
【详解】根据题意得:
总人数是:26÷52%=50人,
所以乘车部分所对应的人数为:×50=20人;
故答案为20人.
【点睛】本题考查了扇形统计图,关键在于求出总人数.
13.【分析】由表中信息可得:根据37°及以下为12人,所占百分比为24%,可求出总人数为:12÷24%=50人;
则37~38°的人数为:50-12-14-8-6=10人;
所以在这些病人中,体温超过37°(不包括37°)的流感患者共有10+14+8+6=38人.
【详解】总人数12÷24%=50人,50×20%=10人,10+14+8+6=38人.
【点睛】本题主要考查了统计表.
14.73【分析】某城市30天的日平均气温中,26℃的有6天,即在样本中比例为 ,故该城市一年365天中日平均气温为26℃的天数即可解答.
【详解】解析: .
【点睛】此题考查用样本估计总体,解题关键在于得出26℃的有6天
15.480.【详解】试题分析:总人数是:10÷20%=50(人),第四小组的人数是:50﹣4﹣10﹣16﹣6﹣4=10,所以该校九年级女生“一分钟跳绳”成绩为优秀的人数是:×1200=480,故答案为480.
考点:频数(率)分布直方图;用样本估计总体;扇形统计图.
16.(1)名;90人(2);(3)人.【分析】(1)根据A组有150人,占总人数的50%,据此即可求得总人数,求出300-150-60的值,即可求出其中“较注意节约用水”的学生;(2)360°乘以B组所占的比例即可求得圆心角;
(3)用3000人乘以C组所占的比例即可求解.
【详解】(1)150÷50%=300(名),300 150 60=90(人),
答:这次调查问卷调查共调查了300名学生,其中“较注意节约用水”的学生有90人;
(2)360°× =108°.
答:在扇形统计图中,“B”所对应的扇形的圆心角度数是108°;
(3)3000× =600(人).
答:估计该校“不注意解决用水”的学生人数为600人.
【点睛】本题主要考查了条形统计图,用样本估计总体,扇形统计图的综合.
17.(1)40%;(2)219;(3)减少废气的排放.(答案不唯一)【分析】( 1 )从题表中可以看出空气质量为轻微污染的天数为7+4+1=12 ,故其所占的百分比为12÷30× 100%=40%.
( 2 )从题表中可以看出30天中有3+5+10=18天空气质量达到良以上,所以一年中约有
18 ÷30× 365=219(天)空气质量达到良以上.
( 3 ) 减少废气的排放.
【详解】(1)从表中可以看出空气质量为轻微污染的天数为天,故其占的百分数.
(2)空气质量达到良以上,从表中可以看出有天,所以天;
(3)减少废气的排放.
【点睛】本题是一道统计题,难点在于从统计表中获取数据进行解答.
18.(1)详见解析(2)详见解析【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】(1)总体是某块玉米实验田里的单株产量,个体是试验田里每株玉米的产量,样本是抽取的株玉米的单株产量.
(2)总体是某校学生完成课外作业的时间,个体是学校每名学生完成课外作业的时间,样本是抽样调查的名学生完成课外作业的时间.
【点睛】本题考查了总体、个体、样本、样本容量的概念.
19.(1)折线统计图;(2)扇形统计图;(3)条形统计图【分析】(1)折线统计图表示的是事物的变化情况;
(2)扇形统计图直接反映部分占总体的百分比大小;
(3)条形统计图能清楚地表示出每个项目的数据.
【详解】(1)从折线统计图可以看出各个季度用电量变化情况;
(2)冰箱用电量超过总用电量的,就是要知道部分占总体的百分比大小,可以从扇形统计图可以看出;
(3)空调的用电量就是要知道项目的数据,可以从条形统计图可以看出.
【点睛】此题考查扇形统计图,条形统计图,解题关键在于掌握统计图的的意义
20. 101; 20200【分析】根据求平均数的方法求解5棵树的平均数;然后乘以200,即为总重量.
【详解】解:5棵果树的平均产量=(98+102+97+103+105)5=101(千克);
估计这200棵果树的总产量为101200=20200(千克).
故答案为101;20200.
【点睛】本题考查了平均数的计算,学会用样本估计总体.
一、单选题
1.一名同学调查了全班名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
最喜欢的节目类别 划记 人数 百分数(%)
相声 正
小品 正正正一
歌曲 正正
舞蹈 正一
其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )A.相声 B.小品 C.歌曲 D.舞蹈
2.如图,一个正在绘制的扇形统计图,整个圆表示某班参加体育活动的总人数,那么表示参加实心球训练的人数占总人数的的扇形是( )
A. B. C. D.
3.要了解一批电视机的使用寿命,从中任意抽取台电视机进行试验,在这个问题中,40是( )
A.个体 B.总体 C.样本容量 D.总体的一个样本
4.我市某中学为了了解年度下学期七年级数学学科期中考试分数段成绩的分布情况,从全校七年级名学生中抽取了名学生的期中数学成绩进行调查,在这次调查中,样本是( )
A.名学生 B.名学生的期中数学成绩
C.名学生 D.名学生的期中数学成绩
5.某市有5500名学生参加考试,为了了解考试情况,从中抽取1000名学生的成绩进行统计分析,在这个问题中,有下列三种说法:①1000名考生是总体的一个样本;②5500名考生是总体;③样本容量是1000.其中正确的说法有( )
A.0种 B.1种 C.2种 D.3种
6.老师对某班全体学生在电脑培训前后进行了一次水平测试,考分以同一标准划分为“不合格”、“合格”、“优秀”三个等级,成绩见下表.下列说法错误的是( )
A.培训前“不合格”的学生占80%
B.培训前成绩“合格”的学生是“优秀”学生的4倍
C.培训后80%的学生成绩达到了“合格”以上
D.培训后优秀率提高了30%
7.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( )
A.2013年昆明市九年级学生是总体 B.每一名九年级学生是个体
C.1000名九年级学生是总体的一个样本 D.样本容量是1000
8.(2016山东省泰安市)某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
9.(2016山东省泰安市)某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E、F的人数分别为80,70
D.喜欢选修课C的人数最少
10.某校公布了该校反映各年级学生体育达标情况的两张统计图(如图),该校七、八、九三个年级共有学生800人.甲、乙、丙三个同学看了这两张统计图后,甲说:“七年级的体育达标率最高.”乙说:“八年级共有学生264人.”丙说:“九年级的体育达标率最高.”甲、乙、丙三个同学中,说法正确的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.甲、乙和丙
二、填空题
11.妈妈做了一份美味可口的菜品,为了了解菜品的咸淡是否适合,于是妈妈取了一点品尝,这应该属于___________(填普查或抽样调查)
12.某班主任把本班学生上学方式的调查结果绘制成如图所示的不完整的统计图,已知骑自行车上学的学生有人,乘坐公交车上学学生对应的扇形所占的圆心角的度数,则乘公交车上学的学生人数为__________.
13.如图,某医院护士为一群流感患者测量体温并制成统计图表,在这些病人中,体温超过(不包括)的流感患者共有__________人.
14.随机抽取某城市一年(以365天计)中的30天的日平均气温状况统计如下:
温度(℃) 10 14 18 22 26 30 32
天数 3 5 5 7 6 2 2
则可估计该城市一年中日平均气温为26 ℃的约有_________天.
15.(2016福建省莆田市)在大课间活动中,同学们积极参加体育锻炼,小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,估计该校学生“一分钟跳绳”成绩优秀的人数为__________人.
三、解答题
16.为响应“三节三爱”号召,我校把用电习惯分为“很注意节约用电()”、“较注意节约用电()”“不注意节约用电()”三类情况,设计了调查问卷在中学生中开展调查,并将调查结果分析整理后,制成如图所示的两个统计图.
请根据以上信息解答下列问题:
(1)这次问卷调查共调查了多少名学生?其中“较注意节约用水”的学生有多少人?
(2)在扇形统计图中,“”所对应的扇形的圆心角度数是多少?
(3)如果设该校共有学生人,试估计“不注意节约用电”的学生人数.
17.随机抽取某城市天的空气质量状况统计如下:
污染指数()
天数()
(其中时,空气质量为优;时,空气质量为良;时,空气质量为轻微污染)
(1)这天中,空气质量为轻微污染的天数所占的百分数是多少?
(2)估计该城市一年(以天记)中有多少天空气质量到良以上?
(3)保护环境人人有责,请说出一种保护环境的好方法.
18.指出下列问题中的总体、个体、样本:
(1)为了估计某块玉米试验田里的单株平均产量,从中抽取株进行实测;
(2)某学校为了了解学生完成课外作业的时间,从中抽样调查了名学生完成课外作业的时间进行分析.
19.小明家2002年四个季度的用电量如下:
季度名称 用电量(单位:千瓦时)
第一季度 250
第二季度 150
第三季度 400
第四季度 200
其中各种电器用电量如下表:
各种电器 用电量(单位:千瓦时)
空调 250
冰箱 400
照明 100
彩电 150
其他 100
小明根据上面的数据制成下面的统计图.
根据以上三幅统计图回答:
(1)从哪幅统计图中可以看出各个季度用电量变化情况?
(2)从哪幅统计图中可以看出冰箱用电量超过总用电量的?
(3)从哪幅统计图中可以清楚地看出空调的用电量?
20.果园里有果树200棵,从中随机抽取5棵,每棵果树的产量如下(单位:kg):98,102,97,103,105,这5棵果树的平均产量为________kg,估计这200棵果树的总产量为________kg.
参考答案:
1.D【分析】此题只需根据划记的人数除以总人数,正确计算百分比,即可进行分析判断.
【详解】由统计表可得:
A. 相声划记应为5人,则百分数应为 ×100%=10%,故错误;
B. 小品划记应为16人,则百分数应为×100%=32%,故错误;
C. 歌曲划记为应10人,则百分数则百分数应为×100%=20%,故错误;
D. 舞蹈的划记为6人是正确的,百分数为×100%=12%,百分数也正确,故正确.
故选D.
【点睛】本题主要考查了统计表,较为简单.
2.D【分析】首先根据扇形G的圆心角为90°可得参加此训练的人数占总数的25%,再根据35%>25%,可得扇形的面积一定比G大,根据图可选出答案.
【详解】∵扇形G的圆心角为90°,
∴表示参加此训练的人数占总数的:90°÷360°×100%=25%,
∵35%>25%,
∴扇形的面积一定比G大,
∴表示参加实心球训练的人数占总人数的35%的扇形是H,
故选D.
【点睛】本题主要考查了扇形统计图.
3.C【分析】首先找出考查的对象是电视机的使用寿命,从中任意抽取40台电视机,40是指抽取的样本的个数,即样本容量.
【详解】本题中任意抽取的40台电视机是样本,对于其中的40,只是样本中个体的数目,所以是样本容量.故选C.
【点睛】本题主要考查了样本容量的概念,注意样本和样本容量的区别.
4.D【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,据此即可判断.
【详解】在这次调查中,样本是:200名学生的期末数学成绩;
故选D.
【点睛】本题主要考查了样本的概念,牢牢掌握样本的概念是解答本题的关键.
5.B【分析】根据总体:我们把所要考察的对象的全体叫做总体;个体:把组成总体的每一个考察对象叫做个体;样本:从总体中取出的一部分个体叫做这个总体的一个样本;样本容量:一个样本包括的个体数量叫做样本容量分别进行分析即可.
【详解】解:抽取的1000名学生的成绩是一个样本,故①错误;
5500名考生的考试成绩是总体,故②错误;
因为从中抽取1000名学生的成绩,所以样本容量是1000,故③正确.
故选B.
【点睛】此题主要考查了总体、个体、样本、样本容量,关键是掌握各个量的定义.
6.D【分析】此题只需根据统计表分别计算要求的数据,即可进行正确判断.
【详解】解:A、 =80%,故正确;
B、“优秀”学生为2人,所以培训前成绩“合格”的学生是“优秀”学生的4倍,故正确;
C、×100%=80%,故正确;
D、培训后优秀率:×100%=30%,培训前优秀率:×100%=4%,30%-4%=26%,所以培训后优秀率提高了26%,故错误.
故选D.
【点睛】本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
7.D【分析】根据总体、个体、样本、样本容量的概念结合选项选出正确答案即可.
【详解】A、2013年昆明市九年级学生的数学成绩是总体,原说法错误,故本选项不符合题意;
B、每一名九年级学生的数学成绩是个体,原说法错误,故本选项不符合题意;
C、1000名九年级学生的数学成绩是总体的一个样本,原说法错误,故本选项不符合题意;
D、样本容量是1000,该说法正确,故本选项符合题意.
故选:D.
8.D【分析】通过计算得出选项A、B、C正确,选项D错误,即可得出结论.
【详解】解:被调查的学生人数为60÷15%=400(人),∴选项A正确;
扇形统计图中D的圆心角为×360°=90°,∵×360°=36°,
360°(17.5%+15%+12.5%)=162°,
∴扇形统计图中E的圆心角=360°﹣162°﹣90°﹣36°=72°,
∴选项B正确;
∵400×=80(人),400×17.5%=70(人),∴选项C正确;
∵12.5%>10%, ∴喜欢选修课A的人数最少,∴选项D错误;
9.D【分析】通过计算得出选项A、B、C正确,选项D错误,即可得出结论.
【详解】解:被调查的学生人数为60÷15%=400(人),∴选项A正确;
扇形统计图中D的圆心角为×360°=90°,∵×360°=36°,
360°(17.5%+15%+12.5%)=162°,
∴扇形统计图中E的圆心角=360°﹣162°﹣90°﹣36°=72°,
∴选项B正确;
∵400×=80(人),400×17.5%=70(人),∴选项C正确;
∵12.5%>10%, ∴喜欢选修课A的人数最少,∴选项D错误;
10.B【详解】试题分析:由扇形统计图可以看出:八年级共有学生800×33%=264人;
七年级的达标率为;
九年级的达标率为;
八年级的达标率为.
则九年级的达标率最高.则乙、丙的说法是正确的,
故选B.
考点:1.扇形统计图;2.条形统计图.
11.抽样调查【分析】根据普查和抽样调查的定义,显然此题属于抽样调查.
【详解】由于只是取了一点品尝,所以应该是抽样调查.
故答案为:抽样调查.
【点睛】此题考查抽样调查和全面调查,解题关键在于掌握选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查,事关重大的调查往往选用普查.
12.20人【分析】先根据骑自行车上学的学生有26人占52%,求出总人数,再根据乘车部分所对应的圆心角的度数即可求出答案;
【详解】根据题意得:
总人数是:26÷52%=50人,
所以乘车部分所对应的人数为:×50=20人;
故答案为20人.
【点睛】本题考查了扇形统计图,关键在于求出总人数.
13.【分析】由表中信息可得:根据37°及以下为12人,所占百分比为24%,可求出总人数为:12÷24%=50人;
则37~38°的人数为:50-12-14-8-6=10人;
所以在这些病人中,体温超过37°(不包括37°)的流感患者共有10+14+8+6=38人.
【详解】总人数12÷24%=50人,50×20%=10人,10+14+8+6=38人.
【点睛】本题主要考查了统计表.
14.73【分析】某城市30天的日平均气温中,26℃的有6天,即在样本中比例为 ,故该城市一年365天中日平均气温为26℃的天数即可解答.
【详解】解析: .
【点睛】此题考查用样本估计总体,解题关键在于得出26℃的有6天
15.480.【详解】试题分析:总人数是:10÷20%=50(人),第四小组的人数是:50﹣4﹣10﹣16﹣6﹣4=10,所以该校九年级女生“一分钟跳绳”成绩为优秀的人数是:×1200=480,故答案为480.
考点:频数(率)分布直方图;用样本估计总体;扇形统计图.
16.(1)名;90人(2);(3)人.【分析】(1)根据A组有150人,占总人数的50%,据此即可求得总人数,求出300-150-60的值,即可求出其中“较注意节约用水”的学生;(2)360°乘以B组所占的比例即可求得圆心角;
(3)用3000人乘以C组所占的比例即可求解.
【详解】(1)150÷50%=300(名),300 150 60=90(人),
答:这次调查问卷调查共调查了300名学生,其中“较注意节约用水”的学生有90人;
(2)360°× =108°.
答:在扇形统计图中,“B”所对应的扇形的圆心角度数是108°;
(3)3000× =600(人).
答:估计该校“不注意解决用水”的学生人数为600人.
【点睛】本题主要考查了条形统计图,用样本估计总体,扇形统计图的综合.
17.(1)40%;(2)219;(3)减少废气的排放.(答案不唯一)【分析】( 1 )从题表中可以看出空气质量为轻微污染的天数为7+4+1=12 ,故其所占的百分比为12÷30× 100%=40%.
( 2 )从题表中可以看出30天中有3+5+10=18天空气质量达到良以上,所以一年中约有
18 ÷30× 365=219(天)空气质量达到良以上.
( 3 ) 减少废气的排放.
【详解】(1)从表中可以看出空气质量为轻微污染的天数为天,故其占的百分数.
(2)空气质量达到良以上,从表中可以看出有天,所以天;
(3)减少废气的排放.
【点睛】本题是一道统计题,难点在于从统计表中获取数据进行解答.
18.(1)详见解析(2)详见解析【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【详解】(1)总体是某块玉米实验田里的单株产量,个体是试验田里每株玉米的产量,样本是抽取的株玉米的单株产量.
(2)总体是某校学生完成课外作业的时间,个体是学校每名学生完成课外作业的时间,样本是抽样调查的名学生完成课外作业的时间.
【点睛】本题考查了总体、个体、样本、样本容量的概念.
19.(1)折线统计图;(2)扇形统计图;(3)条形统计图【分析】(1)折线统计图表示的是事物的变化情况;
(2)扇形统计图直接反映部分占总体的百分比大小;
(3)条形统计图能清楚地表示出每个项目的数据.
【详解】(1)从折线统计图可以看出各个季度用电量变化情况;
(2)冰箱用电量超过总用电量的,就是要知道部分占总体的百分比大小,可以从扇形统计图可以看出;
(3)空调的用电量就是要知道项目的数据,可以从条形统计图可以看出.
【点睛】此题考查扇形统计图,条形统计图,解题关键在于掌握统计图的的意义
20. 101; 20200【分析】根据求平均数的方法求解5棵树的平均数;然后乘以200,即为总重量.
【详解】解:5棵果树的平均产量=(98+102+97+103+105)5=101(千克);
估计这200棵果树的总产量为101200=20200(千克).
故答案为101;20200.
【点睛】本题考查了平均数的计算,学会用样本估计总体.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
