【精选备课】2022年秋数学青岛版七年级上册 第五章 代数式与函数的初步认识 复习与测试(含解析)
文档属性
| 名称 | 【精选备课】2022年秋数学青岛版七年级上册 第五章 代数式与函数的初步认识 复习与测试(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 191.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 12:18:57 | ||
图片预览




文档简介
第五章 复习与测试
一、单选题
1.某商品进价为每件元,商店将价格提高作零售价销售,在销售旺季过后,商店又以折的价格开展促销活动,这时该商品每件的售价为( )
A.元 B.元 C.元 D.元
2.下列图表列出了一项实验的统计数据,表示将皮球从高d处落下时,弹跳高度b与下落高度d的关系:则能反映这种关系的式子是( )
d 50 80 100 150
b 25 40 50 75
A.b=d2 B.b=2d C.b= D.b=d-25
3.下表是某报纸公布的世界人口数据情况:表中的变量是( )
年份 1957 1974 1987 1999 2025 2050
人口/亿 30亿 40亿 50亿 60亿 80亿 90亿
A.仅有一个,是时间(年份) B.仅有一个,是人口数(亿)
C.有两个,是时间和人口数 D.一个也没有
4.给出下列关于变量x,y的关系式,其中y是x函数的是( )
①3x-2y=5;②y=:③2x-y2=10
A.①②③ B.①② C.①③ D.②③
5.若代数式4y2+6y+5的值是7,则代数式2y2+3y+7的值是( )
A.9 B.13 C.6 D.8
6.下列式子中代数式的个数为( )
①-2ab,②π,③s=(a+b)h,④x+3≥y,⑤a(b+c)=ab=ac,⑥1+2
A.2 B.3 C.4 D.5
7.油箱中有油,油从管道中匀速流出,流完.油箱中剩余油量Q与流出的时间t(min)间的函数关系式是( )
A. B. C. D.
8.当x=-3时,代数式的值为( )
A. B. C. D.
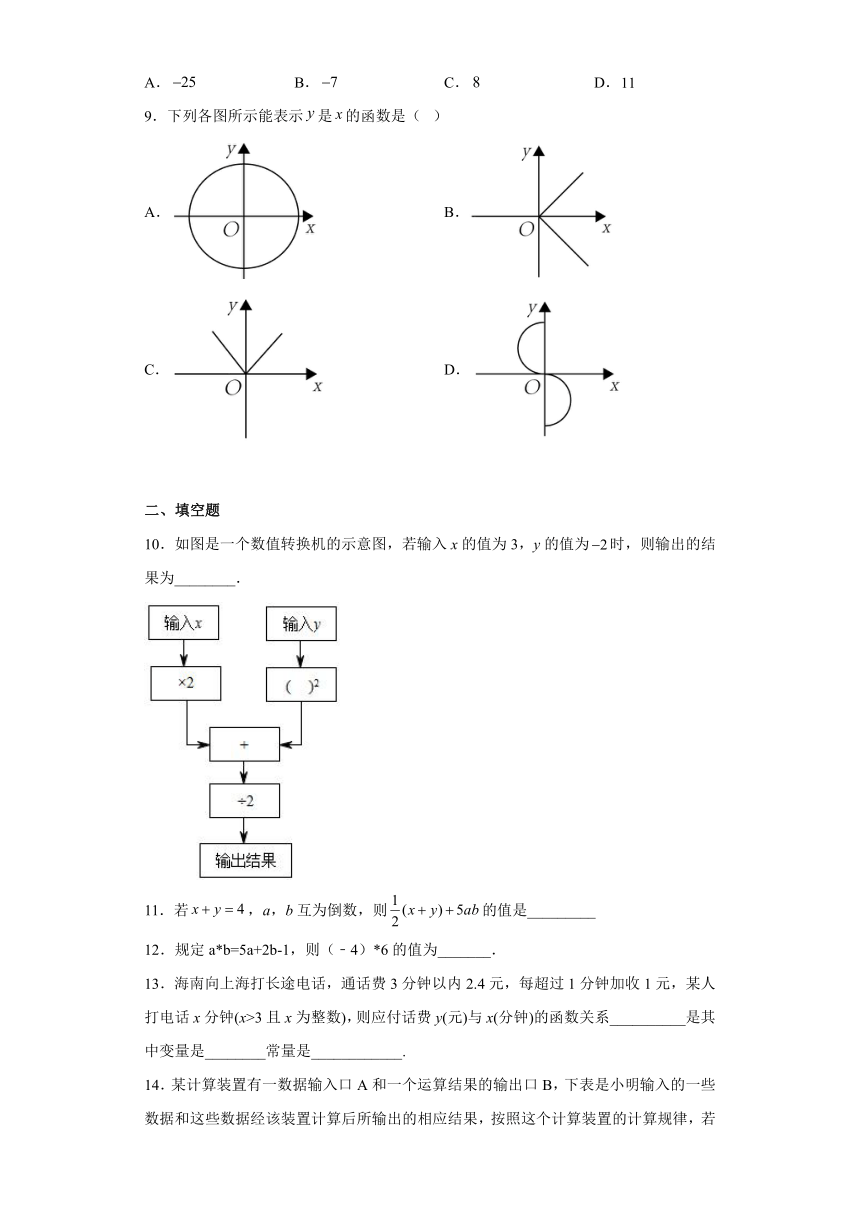
9.下列各图所示能表示是的函数是( )
A. B.
C. D.
二、填空题
10.如图是一个数值转换机的示意图,若输入x的值为3,y的值为时,则输出的结果为________.
11.若,a,b互为倒数,则的值是_________
12.规定a*b=5a+2b-1,则(﹣4)*6的值为_______.
13.海南向上海打长途电话,通话费3分钟以内2.4元,每超过1分钟加收1元,某人打电话x分钟(x>3且x为整数),则应付话费y(元)与x(分钟)的函数关系__________是其中变量是________常量是____________.
14.某计算装置有一数据输入口A和一个运算结果的输出口B,下表是小明输入的一些数据和这些数据经该装置计算后所输出的相应结果,按照这个计算装置的计算规律,若输入的数据是10.则输出的数是_______.
A 1 2 3 4 5 …
B 2 5 10 17 26 …
15.黑白两种颜色的正方形纸片,按如图所示的规律拼成若干个图案:
第4个图案中有白色纸片________块,第n个图案中有白色纸片________块.
16.当x=1时,代数式的值为2012,则当x=-1时,代数式 的值为_____.
三、解答题
17.现定义两种运算:,对于任意整数a,b有ab=a+b-1,ab=ab-1.例如:23=2+3-1,23=2×3-1求(68)(33)的值
18.当a=5,b=-2时,分别求代数式(a-b)2与a2-2ab+b2的值,然后请回答:
(1)这两个代数式的值有什么关系
(2)如果取另对a、b的值.上述结论还成立吗 请你验证.
19.开通了,中国联通公布了资费标准,其中包月186元时,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 1 2 3 4 5 …
电话费/元 0.36 0.72 1.08 1.44 1.80 …
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的关系式是什么?
(3)如果打电话超出分钟,需多付多少电话费?
(4)某次打电话的费用超出部分是元,那么小明的爸爸打电话超出几分钟?
20.如图,当x=5.5,y=4时,求阴影部分的周长和面积.
参考答案:
1.C【分析】根据题意列出等量关系,商品的售价=原售价的80%.直接列代数式求值即可.
【详解】依题意可得:
元.
故选:C.
【点睛】本题主要考查了列代数式问题,解决问题的关键是读懂题意,找到所求的量的等量关系.注意数字通常写在字母的前面.
2.C【分析】这是一个用图表表示的函数,可以看出d是b的2倍,即可得关系式.
【详解】解:由统计数据可知:d是b的2倍,
所以,d=2b,即b=.
故选C.
【点睛】本题考查根据实际问题列一次函数的关系式,解题的关键是读懂题意.
3.C【分析】根据事物的变化过程中发生变化的量是变量,数值不变的量是常量,可得答案.
【详解】解;观察表格,得
时间在变,人口数在变,故C正确.
故选C.
【点睛】本题考查常量与变量,解题的关键是能够了解常量与变量的定义.
4.B【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可确定函数的个数.
【详解】解:①3x-2y=5,②y=|x|,y是x的函数,③2x-y2=10不是函数,
故选B.
【点睛】本题考查函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
5.D【分析】根据已知求出2y2+3y=1,再代入求出即可.
【详解】解:根据题意得:4y2+6y+5=7,
4y2+6y=2,
2y2+3y=1,
所以2y2+3y+7=1+7=8.
故选D.
【点睛】本题考查求代数式的值,能够整体代入是解题的关键.
6.B【分析】代数式即用运算符号把数与字母连起来的式子,根据这一概念进行分析.
【详解】解:根据代数式的定义,可知①、②、⑥都是代数式.
故选B.
【点睛】本题考查代数式的概念.注意代数式中不含有关系符号,即不含有=、≠、<、>、≤、≥等符号.
7.C【分析】根据题意,首先列式(20÷100),计算出从管道中每分钟流出的油量;接下来根据油的流速和时间t的关系,可得到流出油量是0.2t;进而由“剩油量=存油量-流出油量”列出关系式,将得到的关系式与各个选项比较即可得到答案.
【详解】由已知得从管道中每分钟流出的油为20÷100=0.2(L)
所以油箱中剩余油量Q=20-0.2t,
所以油箱中剩余油量Q(L)与流出时间t(min)之间的函数关系式为Q=20-0.2t.
故选C.
【点睛】此题考查函数关系式,解题关键在于利用“剩油量=存油量-流出油量”列出关系式
8.D【分析】把x=-3代入代数式进行计算即可得解.
【详解】将代入代数式,得(-3) -3×(-3)-7=11
故选D
【点睛】此题考查代数式求值,解题关键在于把x=-3代入代数式
9.C【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此对各选项分析判断.
【详解】解:A、对于x的每一个取值,y有时有两个确定的值与之对应,所以y不是x的函数,故本选项错误;
B、对于x的每一个取值,y有时有两个确定的值与之对应,所以y不是x的函数,故本选项错误;
C、对于x的每一个取值,y只有唯一确定的值与之对应,所以y是x的函数,故本选项正确;
D、对于x的每一个取值,y有时有两个确定的值与之对应,所以y不是x的函数,故本选项错误.
故选:C.
【点睛】本题主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
10.5【分析】首先根据已知一个数值转换机的示意图,逐步列出代数式并化简,最后表示出输出的结果的代数式,然后代入求值.
【详解】解:根据已知一个数值转换机的示意图可得:
,,
,
把,代入得:
,
故答案为:5.
【点睛】此题考查了代数式求值问题的理解和掌握.根据示意图正确列出代数式是解题的关键.
11.7【分析】根据a,b互为倒数,可得ab=1;然后把,ab=1代入,计算即可.
【详解】解:∵a,b互为倒数,
∴ab=1,
又∵,
∴
=×4+5×1
=2+5
=7.
故答案为7.
【点睛】本题考查代数式求值、倒数的概念、整体代入的思想,解题的关键是要明确:互为倒数的两个数的乘积是1.
12.-9【分析】根据a*b=5a+2b-1,可以求得题目中所求式子的值,本题得以解决.
【详解】∵a*b=5a+2b-1,
∴(-4)*6
=5×(-4)+2×6-1
=(-20)+12-1
=-9,
故答案为-9.
【点睛】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
13. y=2.4+(x-3), 变量是x,y, 常量是2.4,3.【分析】根据题意首先可以得出只要通话时间不超过3分钟收费均为2.4元,超过3分钟后,每分钟加收1元,由此可列出一次函数关系式.然后根据常量变量的定义进行填空即可.
【详解】解:由题意得,通话时间不超过3分钟收费均为2.4元,超过3分钟后,每分钟加收1元,x>3且x为整数,
故可得函数关系式为:y=2.4+(x-3)(x>3且x为整数),
变量是x,y,;常量是2.4,3.
故答案为y=2.4+(x-3),变量是x,y,常量是2.4,3.
【点睛】本题考查函数关系式,掌握函数的表示方法以及常量变量的定义是解题的关键.
14.101【分析】根据题意和表格,得出A和B的关系式,当A=n时,B=n2+1,再把n=10代入即可求出输出的数.
【详解】解:根据题意和图表可知,
当A=1时,B=2=12+1,
当A=2时,B=5=22+1,
当A=3时,B=10=32+1,
…,
当A=n时,B=n2+1,
当A=10时,B=102+1=100+1=101,
则当输入的数是10时,输出的数是101.
故答案为101.
【点睛】本题考查数字的变化类,解题关键是从图表给出的数据找出A和B的关系式,当A=n时,B=n2+1.
15. 13 3n+1【分析】(1)先求出每一个图案的白色纸片的块数,找出规律,后一个图案比前一个图案的白色纸片多3块,然后写出第4个图案的表示纸片的块数;
(2)观察图形,后面的图案比前面的图案多3个白色纸片,然后写出第n个图案的白色纸片即可.
【详解】解:第1个图案有白色纸片有:4=3+1块,
第2个图案有白色纸片有:7=3×2+1块,
第3个图案有白色纸片有:10=3×3+1块,
(1)第4个图案有白色纸片有: 3×4+1=13块,
…
(2)第n个图案有白色纸片:3n+1块,
故答案为(1)13;(2)3n+1.
【点睛】本题是对图形变化规律的考查,观察出后面的图案比前面的图案多3个白色纸片是解题的关键.
16.-2010【分析】由当x=1时,代数式的值为2012,可得,把x=-1代入代数式整理后,再把代入计算即可.
【详解】因为当时,
,
所以,
所以当时,
.
【点睛】本题考查了求代数式的值,把所给字母代入代数式时,要补上必要的括号和运算符号,然后按照有理数的运算顺序计算即可,熟练掌握有理数的运算法则是解答本题的关键.在求代数式的值时,一般先化简,再把各字母的取值代入求值.有时题目并未给出各个字母的取值,而是给出一个或几个式子的值,这时可以把这一个或几个式子看作一个整体,将待求式化为含有这一个或几个式子的形式,再代入求值.运用整体代换,往往能使问题得到简化.
17.20.【分析】首先理解两种运算“”“”的规定,然后按照混合运算的顺序,有括号的先算括号里面的,本题先算68,33,再把它们的结果用“”计算.
【详解】解:∵68=6+8-1=13,
33=3×3-1=8,
∴(68)(33)=138=13+8-1=20.
故答案为20.
【点睛】本题考查定义新运算题型,关键是读懂题意,得出新运算的顺序.
18.(1)相等;(2)成立,例如取a=1,b=2.【分析】(1)把a=5,b=-2分别求代数式(a-b)2和a2-2ab+b2计算,根据代数式的值判断即可;
(2)取a=1,b=2计算得到两个代数式的值相等,可得上述结论还成立.
【详解】解:(1)当a=5,b=-2时,
(a-b)2=(5+2)2=49,
a2-2ab+b2=25+20+4=49;
∴这两个代数式的值相等;
(2)取a=1,b=2,则
(a-b)2=(1-2)2=1,
a2-2ab+b2=1-4+4=1,
∴上述结论还成立.
故答案为(1)相等;(2)成立,例如取a=1,b=2.
【点睛】本题考查代数式求值,属于探究型试题,弄清题意是解本题的关键.
19.(1)国内拨打时间与电话费之间的关系,打电话时间是自变量、电话费是因变量;(2)y=0.36x;(3)3.6元;(4)小明的爸爸打电话超出15分钟.【分析】(1)根据图表可以知道:电话费随时间的变化而变化,因而打电话时间是自变量、电话费是因变量;
(2)费用=单价×时间,即可写出解析式;
(3)把x=10代入解析式即可求得;
(4)在解析式中令y=5.4即可求得x的值.
【详解】解:(1)国内拨打时间与电话费之间的关系,打电话时间是自变量、电话费是因变量;
(2)由题意可得:y=0.36x;
(3)当x=10时,(元);即:需多付3.6元电话费.
(4)当时,(分钟).
答:小明的爸爸打电话超出15分钟.
【点睛】本题比较容易,考查求函数值.
(1)当已知函数解析式时,求函数值就是求代数式的值;
(2)函数值是唯一的,而对应的自变量可以是多个.
20.阴影部分的周长为46,阴影部分的面积为77.【分析】根据周长的定义列式,然后把x、y的值代入进行计算即可得解;
用长方形的面积减去缺口的面积,再把x、y的值代入进行计算即可得解.
【详解】阴影部分的周长为=2(2x+2y)+2y
∵x=5.5,y=4,
∴周长=4×5.5+6×4=22+24=46;
阴影部分的面积=2x 2y-y(2x-0.5x-x)=4xy-0.5xy=3.5xy,
∵x=5.5,y=4,
∴面积=3.5×5.5×4=77.
【点睛】本题考查了列代数式,代数式求值,主要利用了周长与面积的定义,仔细观察图形,得到面积的表示是解题的关键.
一、单选题
1.某商品进价为每件元,商店将价格提高作零售价销售,在销售旺季过后,商店又以折的价格开展促销活动,这时该商品每件的售价为( )
A.元 B.元 C.元 D.元
2.下列图表列出了一项实验的统计数据,表示将皮球从高d处落下时,弹跳高度b与下落高度d的关系:则能反映这种关系的式子是( )
d 50 80 100 150
b 25 40 50 75
A.b=d2 B.b=2d C.b= D.b=d-25
3.下表是某报纸公布的世界人口数据情况:表中的变量是( )
年份 1957 1974 1987 1999 2025 2050
人口/亿 30亿 40亿 50亿 60亿 80亿 90亿
A.仅有一个,是时间(年份) B.仅有一个,是人口数(亿)
C.有两个,是时间和人口数 D.一个也没有
4.给出下列关于变量x,y的关系式,其中y是x函数的是( )
①3x-2y=5;②y=:③2x-y2=10
A.①②③ B.①② C.①③ D.②③
5.若代数式4y2+6y+5的值是7,则代数式2y2+3y+7的值是( )
A.9 B.13 C.6 D.8
6.下列式子中代数式的个数为( )
①-2ab,②π,③s=(a+b)h,④x+3≥y,⑤a(b+c)=ab=ac,⑥1+2
A.2 B.3 C.4 D.5
7.油箱中有油,油从管道中匀速流出,流完.油箱中剩余油量Q与流出的时间t(min)间的函数关系式是( )
A. B. C. D.
8.当x=-3时,代数式的值为( )
A. B. C. D.
9.下列各图所示能表示是的函数是( )
A. B.
C. D.
二、填空题
10.如图是一个数值转换机的示意图,若输入x的值为3,y的值为时,则输出的结果为________.
11.若,a,b互为倒数,则的值是_________
12.规定a*b=5a+2b-1,则(﹣4)*6的值为_______.
13.海南向上海打长途电话,通话费3分钟以内2.4元,每超过1分钟加收1元,某人打电话x分钟(x>3且x为整数),则应付话费y(元)与x(分钟)的函数关系__________是其中变量是________常量是____________.
14.某计算装置有一数据输入口A和一个运算结果的输出口B,下表是小明输入的一些数据和这些数据经该装置计算后所输出的相应结果,按照这个计算装置的计算规律,若输入的数据是10.则输出的数是_______.
A 1 2 3 4 5 …
B 2 5 10 17 26 …
15.黑白两种颜色的正方形纸片,按如图所示的规律拼成若干个图案:
第4个图案中有白色纸片________块,第n个图案中有白色纸片________块.
16.当x=1时,代数式的值为2012,则当x=-1时,代数式 的值为_____.
三、解答题
17.现定义两种运算:,对于任意整数a,b有ab=a+b-1,ab=ab-1.例如:23=2+3-1,23=2×3-1求(68)(33)的值
18.当a=5,b=-2时,分别求代数式(a-b)2与a2-2ab+b2的值,然后请回答:
(1)这两个代数式的值有什么关系
(2)如果取另对a、b的值.上述结论还成立吗 请你验证.
19.开通了,中国联通公布了资费标准,其中包月186元时,超出部分国内拨打0.36元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 1 2 3 4 5 …
电话费/元 0.36 0.72 1.08 1.44 1.80 …
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的关系式是什么?
(3)如果打电话超出分钟,需多付多少电话费?
(4)某次打电话的费用超出部分是元,那么小明的爸爸打电话超出几分钟?
20.如图,当x=5.5,y=4时,求阴影部分的周长和面积.
参考答案:
1.C【分析】根据题意列出等量关系,商品的售价=原售价的80%.直接列代数式求值即可.
【详解】依题意可得:
元.
故选:C.
【点睛】本题主要考查了列代数式问题,解决问题的关键是读懂题意,找到所求的量的等量关系.注意数字通常写在字母的前面.
2.C【分析】这是一个用图表表示的函数,可以看出d是b的2倍,即可得关系式.
【详解】解:由统计数据可知:d是b的2倍,
所以,d=2b,即b=.
故选C.
【点睛】本题考查根据实际问题列一次函数的关系式,解题的关键是读懂题意.
3.C【分析】根据事物的变化过程中发生变化的量是变量,数值不变的量是常量,可得答案.
【详解】解;观察表格,得
时间在变,人口数在变,故C正确.
故选C.
【点睛】本题考查常量与变量,解题的关键是能够了解常量与变量的定义.
4.B【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此即可确定函数的个数.
【详解】解:①3x-2y=5,②y=|x|,y是x的函数,③2x-y2=10不是函数,
故选B.
【点睛】本题考查函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
5.D【分析】根据已知求出2y2+3y=1,再代入求出即可.
【详解】解:根据题意得:4y2+6y+5=7,
4y2+6y=2,
2y2+3y=1,
所以2y2+3y+7=1+7=8.
故选D.
【点睛】本题考查求代数式的值,能够整体代入是解题的关键.
6.B【分析】代数式即用运算符号把数与字母连起来的式子,根据这一概念进行分析.
【详解】解:根据代数式的定义,可知①、②、⑥都是代数式.
故选B.
【点睛】本题考查代数式的概念.注意代数式中不含有关系符号,即不含有=、≠、<、>、≤、≥等符号.
7.C【分析】根据题意,首先列式(20÷100),计算出从管道中每分钟流出的油量;接下来根据油的流速和时间t的关系,可得到流出油量是0.2t;进而由“剩油量=存油量-流出油量”列出关系式,将得到的关系式与各个选项比较即可得到答案.
【详解】由已知得从管道中每分钟流出的油为20÷100=0.2(L)
所以油箱中剩余油量Q=20-0.2t,
所以油箱中剩余油量Q(L)与流出时间t(min)之间的函数关系式为Q=20-0.2t.
故选C.
【点睛】此题考查函数关系式,解题关键在于利用“剩油量=存油量-流出油量”列出关系式
8.D【分析】把x=-3代入代数式进行计算即可得解.
【详解】将代入代数式,得(-3) -3×(-3)-7=11
故选D
【点睛】此题考查代数式求值,解题关键在于把x=-3代入代数式
9.C【分析】根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此对各选项分析判断.
【详解】解:A、对于x的每一个取值,y有时有两个确定的值与之对应,所以y不是x的函数,故本选项错误;
B、对于x的每一个取值,y有时有两个确定的值与之对应,所以y不是x的函数,故本选项错误;
C、对于x的每一个取值,y只有唯一确定的值与之对应,所以y是x的函数,故本选项正确;
D、对于x的每一个取值,y有时有两个确定的值与之对应,所以y不是x的函数,故本选项错误.
故选:C.
【点睛】本题主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
10.5【分析】首先根据已知一个数值转换机的示意图,逐步列出代数式并化简,最后表示出输出的结果的代数式,然后代入求值.
【详解】解:根据已知一个数值转换机的示意图可得:
,,
,
把,代入得:
,
故答案为:5.
【点睛】此题考查了代数式求值问题的理解和掌握.根据示意图正确列出代数式是解题的关键.
11.7【分析】根据a,b互为倒数,可得ab=1;然后把,ab=1代入,计算即可.
【详解】解:∵a,b互为倒数,
∴ab=1,
又∵,
∴
=×4+5×1
=2+5
=7.
故答案为7.
【点睛】本题考查代数式求值、倒数的概念、整体代入的思想,解题的关键是要明确:互为倒数的两个数的乘积是1.
12.-9【分析】根据a*b=5a+2b-1,可以求得题目中所求式子的值,本题得以解决.
【详解】∵a*b=5a+2b-1,
∴(-4)*6
=5×(-4)+2×6-1
=(-20)+12-1
=-9,
故答案为-9.
【点睛】本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.
13. y=2.4+(x-3), 变量是x,y, 常量是2.4,3.【分析】根据题意首先可以得出只要通话时间不超过3分钟收费均为2.4元,超过3分钟后,每分钟加收1元,由此可列出一次函数关系式.然后根据常量变量的定义进行填空即可.
【详解】解:由题意得,通话时间不超过3分钟收费均为2.4元,超过3分钟后,每分钟加收1元,x>3且x为整数,
故可得函数关系式为:y=2.4+(x-3)(x>3且x为整数),
变量是x,y,;常量是2.4,3.
故答案为y=2.4+(x-3),变量是x,y,常量是2.4,3.
【点睛】本题考查函数关系式,掌握函数的表示方法以及常量变量的定义是解题的关键.
14.101【分析】根据题意和表格,得出A和B的关系式,当A=n时,B=n2+1,再把n=10代入即可求出输出的数.
【详解】解:根据题意和图表可知,
当A=1时,B=2=12+1,
当A=2时,B=5=22+1,
当A=3时,B=10=32+1,
…,
当A=n时,B=n2+1,
当A=10时,B=102+1=100+1=101,
则当输入的数是10时,输出的数是101.
故答案为101.
【点睛】本题考查数字的变化类,解题关键是从图表给出的数据找出A和B的关系式,当A=n时,B=n2+1.
15. 13 3n+1【分析】(1)先求出每一个图案的白色纸片的块数,找出规律,后一个图案比前一个图案的白色纸片多3块,然后写出第4个图案的表示纸片的块数;
(2)观察图形,后面的图案比前面的图案多3个白色纸片,然后写出第n个图案的白色纸片即可.
【详解】解:第1个图案有白色纸片有:4=3+1块,
第2个图案有白色纸片有:7=3×2+1块,
第3个图案有白色纸片有:10=3×3+1块,
(1)第4个图案有白色纸片有: 3×4+1=13块,
…
(2)第n个图案有白色纸片:3n+1块,
故答案为(1)13;(2)3n+1.
【点睛】本题是对图形变化规律的考查,观察出后面的图案比前面的图案多3个白色纸片是解题的关键.
16.-2010【分析】由当x=1时,代数式的值为2012,可得,把x=-1代入代数式整理后,再把代入计算即可.
【详解】因为当时,
,
所以,
所以当时,
.
【点睛】本题考查了求代数式的值,把所给字母代入代数式时,要补上必要的括号和运算符号,然后按照有理数的运算顺序计算即可,熟练掌握有理数的运算法则是解答本题的关键.在求代数式的值时,一般先化简,再把各字母的取值代入求值.有时题目并未给出各个字母的取值,而是给出一个或几个式子的值,这时可以把这一个或几个式子看作一个整体,将待求式化为含有这一个或几个式子的形式,再代入求值.运用整体代换,往往能使问题得到简化.
17.20.【分析】首先理解两种运算“”“”的规定,然后按照混合运算的顺序,有括号的先算括号里面的,本题先算68,33,再把它们的结果用“”计算.
【详解】解:∵68=6+8-1=13,
33=3×3-1=8,
∴(68)(33)=138=13+8-1=20.
故答案为20.
【点睛】本题考查定义新运算题型,关键是读懂题意,得出新运算的顺序.
18.(1)相等;(2)成立,例如取a=1,b=2.【分析】(1)把a=5,b=-2分别求代数式(a-b)2和a2-2ab+b2计算,根据代数式的值判断即可;
(2)取a=1,b=2计算得到两个代数式的值相等,可得上述结论还成立.
【详解】解:(1)当a=5,b=-2时,
(a-b)2=(5+2)2=49,
a2-2ab+b2=25+20+4=49;
∴这两个代数式的值相等;
(2)取a=1,b=2,则
(a-b)2=(1-2)2=1,
a2-2ab+b2=1-4+4=1,
∴上述结论还成立.
故答案为(1)相等;(2)成立,例如取a=1,b=2.
【点睛】本题考查代数式求值,属于探究型试题,弄清题意是解本题的关键.
19.(1)国内拨打时间与电话费之间的关系,打电话时间是自变量、电话费是因变量;(2)y=0.36x;(3)3.6元;(4)小明的爸爸打电话超出15分钟.【分析】(1)根据图表可以知道:电话费随时间的变化而变化,因而打电话时间是自变量、电话费是因变量;
(2)费用=单价×时间,即可写出解析式;
(3)把x=10代入解析式即可求得;
(4)在解析式中令y=5.4即可求得x的值.
【详解】解:(1)国内拨打时间与电话费之间的关系,打电话时间是自变量、电话费是因变量;
(2)由题意可得:y=0.36x;
(3)当x=10时,(元);即:需多付3.6元电话费.
(4)当时,(分钟).
答:小明的爸爸打电话超出15分钟.
【点睛】本题比较容易,考查求函数值.
(1)当已知函数解析式时,求函数值就是求代数式的值;
(2)函数值是唯一的,而对应的自变量可以是多个.
20.阴影部分的周长为46,阴影部分的面积为77.【分析】根据周长的定义列式,然后把x、y的值代入进行计算即可得解;
用长方形的面积减去缺口的面积,再把x、y的值代入进行计算即可得解.
【详解】阴影部分的周长为=2(2x+2y)+2y
∵x=5.5,y=4,
∴周长=4×5.5+6×4=22+24=46;
阴影部分的面积=2x 2y-y(2x-0.5x-x)=4xy-0.5xy=3.5xy,
∵x=5.5,y=4,
∴面积=3.5×5.5×4=77.
【点睛】本题考查了列代数式,代数式求值,主要利用了周长与面积的定义,仔细观察图形,得到面积的表示是解题的关键.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
