2022—2023学年北师大版数学九年级上册1.1.1菱形的性质 课件(共14张PPT)
文档属性
| 名称 | 2022—2023学年北师大版数学九年级上册1.1.1菱形的性质 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 713.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 14:41:11 | ||
图片预览



文档简介
(共14张PPT)
第一章 特殊平行四边形
学练优九年级数学上(BS)
教学课件
1.1 菱形的性质
学习目标
1.了解菱形的概念及其与平行四边形的关系.
2.探索并证明菱形的性质定理.(重点)
3.应用菱形的性质定理解决相关计算或证明问题.(难点)
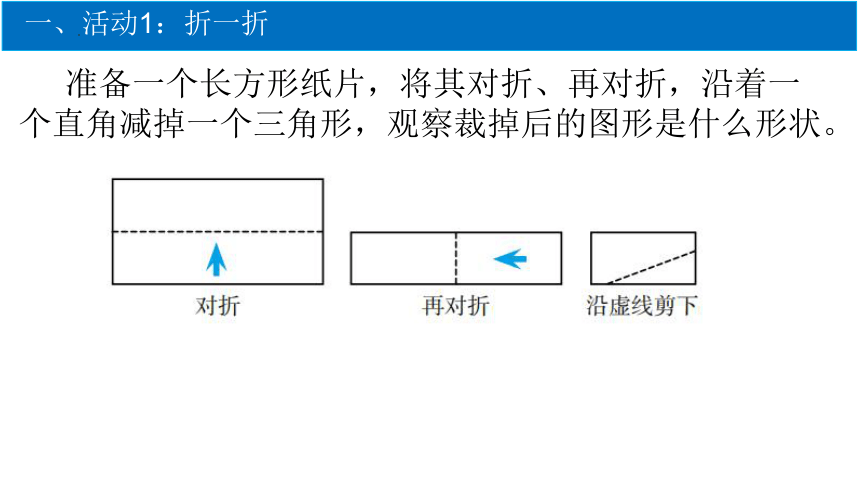
一、活动1:折一折
准备一个长方形纸片,将其对折、再对折,沿着一个直角减掉一个三角形,观察裁掉后的图形是什么形状。
定义:有一组邻边相等的平行四边形.
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
知识小结
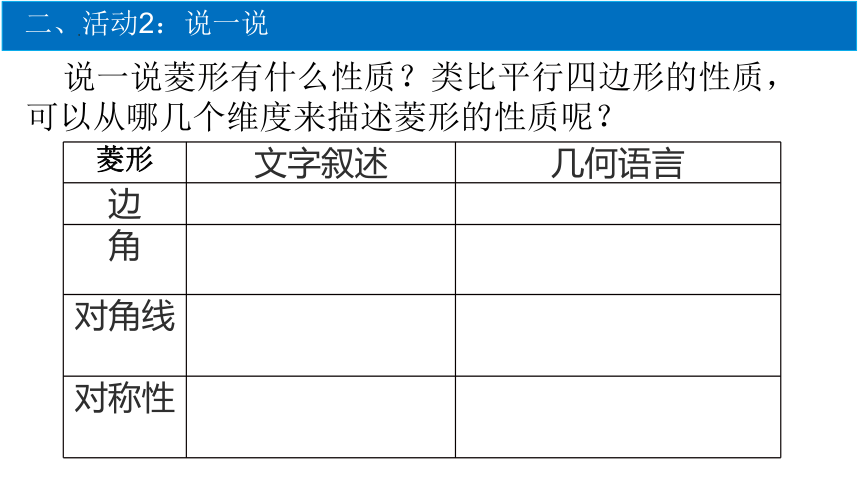
二、活动2:说一说
说一说菱形有什么性质?类比平行四边形的性质,可以从哪几个维度来描述菱形的性质呢?
菱形 文字叙述 几何语言
边
角
对角线
对称性
三、活动3:证一证
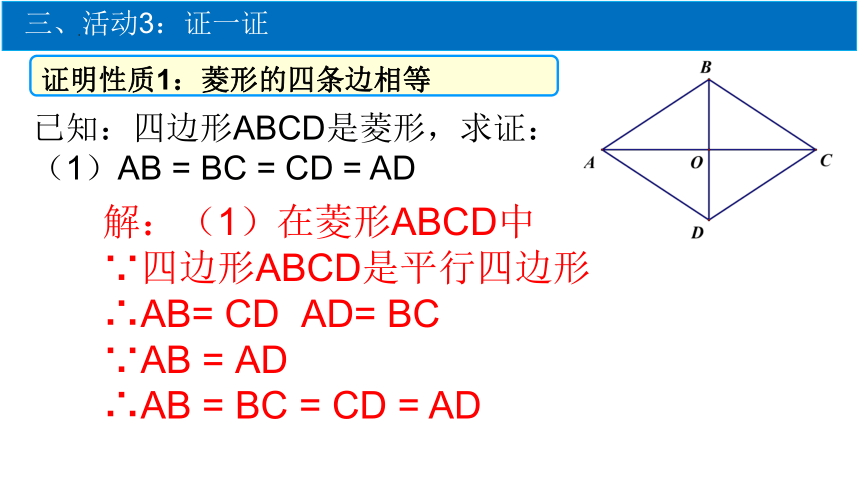
已知:四边形ABCD是菱形,求证:
(1)AB = BC = CD = AD
证明性质1:菱形的四条边相等
解:(1)在菱形ABCD中
∵四边形ABCD是平行四边形
∴AB= CD AD= BC
∵AB = AD
∴AB = BC = CD = AD
三、活动3:证一证
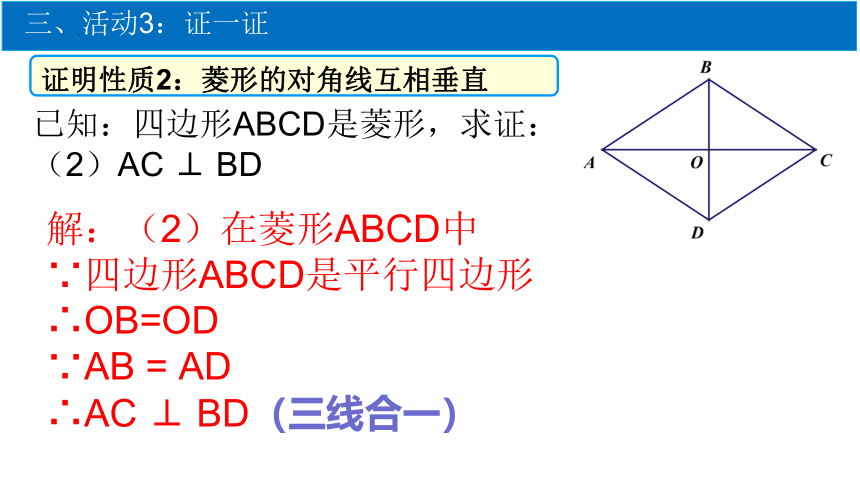
已知:四边形ABCD是菱形,求证:
(2)AC ⊥ BD
证明性质2:菱形的对角线互相垂直
解:(2)在菱形ABCD中
∵四边形ABCD是平行四边形
∴OB=OD
∵AB = AD
∴AC ⊥ BD(三线合一)
三、活动3:证一证
已知:四边形ABCD是菱形,求证:
(3)AC 平分 ∠BAD 和 ∠BCD
BD 平分 ∠ABC 和 ∠ADC
证明性质3:菱形的对角线平分内角
方法1:解:(3)在菱形ABCD中
∵四边形ABCD是平行四边形
∴OB=OD
∵AB = AD
∴AC 平分 ∠BAD (三线合一)
同理AC 平分∠BCD
BD 平分 ∠ABC 和 ∠ADC
方法2 :解:在菱形ABCD中
AB = AD CB=CD
∴在△BAC和△DAC
AB = AD
CB=CD
AC=AC
∴△BAC≌△DAC(SSS)
∴∠BAC=∠DAC
∴AC 平分 ∠BAD
四、活动4:用一用
1.如图,在菱形ABCD中,AC=8,BD=6,求菱形ABCD的周长和面积。
你还能利用其它方法求菱形的面积吗?
四、活动4:用一用
1.如图,在菱形ABCD中,AC=8,BD=6,求菱形ABCD的周长和面积。
四、活动4:用一用
2.在菱形 ABCD 中,∠ BAC=30°, BC=6。
求 :(1)∠ BCD 和∠ ABC 的度数。
(2)对角线 AC、BD 的长。
四、活动4:用一用
2.在菱形 ABCD 中,∠ BAC=30°, BC=6。
求 : (2)对角线 AC、BD 的长。
四、活动4:用一用
2.在菱形 ABCD 中,∠ BAC=30°, BC=6。
求 (3)菱形 ABCD 的面积。
(4)如图,若DH是AB 边上的高,
求 DH 的长。
五、课堂小结
本节课的主要内容是什么?
你有什么收获和困惑?
第一章 特殊平行四边形
学练优九年级数学上(BS)
教学课件
1.1 菱形的性质
学习目标
1.了解菱形的概念及其与平行四边形的关系.
2.探索并证明菱形的性质定理.(重点)
3.应用菱形的性质定理解决相关计算或证明问题.(难点)
一、活动1:折一折
准备一个长方形纸片,将其对折、再对折,沿着一个直角减掉一个三角形,观察裁掉后的图形是什么形状。
定义:有一组邻边相等的平行四边形.
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
知识小结
二、活动2:说一说
说一说菱形有什么性质?类比平行四边形的性质,可以从哪几个维度来描述菱形的性质呢?
菱形 文字叙述 几何语言
边
角
对角线
对称性
三、活动3:证一证
已知:四边形ABCD是菱形,求证:
(1)AB = BC = CD = AD
证明性质1:菱形的四条边相等
解:(1)在菱形ABCD中
∵四边形ABCD是平行四边形
∴AB= CD AD= BC
∵AB = AD
∴AB = BC = CD = AD
三、活动3:证一证
已知:四边形ABCD是菱形,求证:
(2)AC ⊥ BD
证明性质2:菱形的对角线互相垂直
解:(2)在菱形ABCD中
∵四边形ABCD是平行四边形
∴OB=OD
∵AB = AD
∴AC ⊥ BD(三线合一)
三、活动3:证一证
已知:四边形ABCD是菱形,求证:
(3)AC 平分 ∠BAD 和 ∠BCD
BD 平分 ∠ABC 和 ∠ADC
证明性质3:菱形的对角线平分内角
方法1:解:(3)在菱形ABCD中
∵四边形ABCD是平行四边形
∴OB=OD
∵AB = AD
∴AC 平分 ∠BAD (三线合一)
同理AC 平分∠BCD
BD 平分 ∠ABC 和 ∠ADC
方法2 :解:在菱形ABCD中
AB = AD CB=CD
∴在△BAC和△DAC
AB = AD
CB=CD
AC=AC
∴△BAC≌△DAC(SSS)
∴∠BAC=∠DAC
∴AC 平分 ∠BAD
四、活动4:用一用
1.如图,在菱形ABCD中,AC=8,BD=6,求菱形ABCD的周长和面积。
你还能利用其它方法求菱形的面积吗?
四、活动4:用一用
1.如图,在菱形ABCD中,AC=8,BD=6,求菱形ABCD的周长和面积。
四、活动4:用一用
2.在菱形 ABCD 中,∠ BAC=30°, BC=6。
求 :(1)∠ BCD 和∠ ABC 的度数。
(2)对角线 AC、BD 的长。
四、活动4:用一用
2.在菱形 ABCD 中,∠ BAC=30°, BC=6。
求 : (2)对角线 AC、BD 的长。
四、活动4:用一用
2.在菱形 ABCD 中,∠ BAC=30°, BC=6。
求 (3)菱形 ABCD 的面积。
(4)如图,若DH是AB 边上的高,
求 DH 的长。
五、课堂小结
本节课的主要内容是什么?
你有什么收获和困惑?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
