人教版数学八年级下册18.2.3正方形性质与判定 课件(共33张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.3正方形性质与判定 课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 14:43:13 | ||
图片预览










文档简介
(共33张PPT)
正方形
矩形
菱形
平行四边形
有一个角是直角
有一组邻边相等
回顾:特殊的平行四边形
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形叫正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形叫正方形
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形
有一个角是直角的菱形叫做正方形
有一组邻边相等的矩形叫正方形
正方形即是特殊的平行四边形又是特殊的矩形和菱形
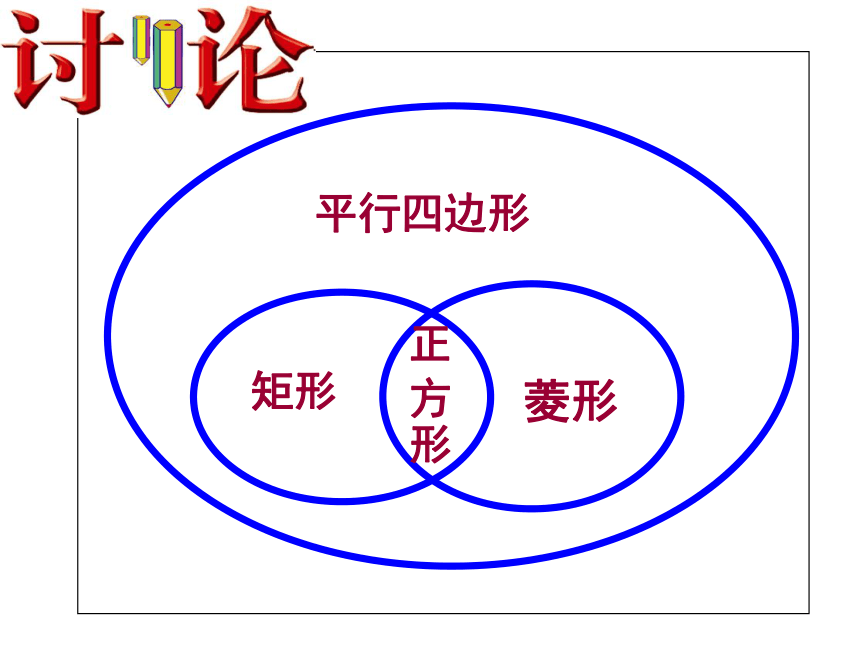
平行四边形,矩形,菱形,正方形的关系!
菱形
矩形
平行四边形
正
形
方
正方形具有平行四边形、矩形、菱形的所有性质
正方形有哪些性质?
正方形的性质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形
C
D
\
\
B
\
A
\
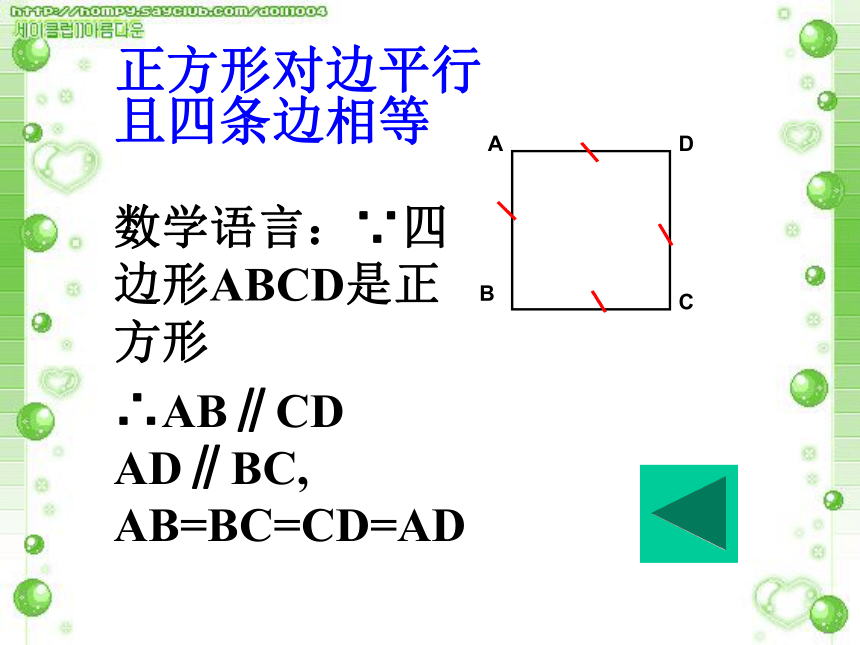
正方形对边平行且四条边相等
数学语言:∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
正方形四个角都是直角
数学语言:∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
A
B
C
D
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
1、正方形具有而菱形不一定具有的性质是( )
(A)四条边相等 (B)对角线互相垂直平分
(C)对角线平分一组对角 (D)对角线相等
2、正方形具有而矩形不一定具有的性质是( )
(A)四个角相等 (B)对角线互相垂直平分
(C)对角线相等 (D)对角互补
3、如图:正方形ABCD的周长为15cm,则矩形EFCG的周长
为 cm。
A
B
C
D
E
G
F
D
B
7.5
6.正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.
课堂练习
4.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.
5
30°
16cm
5.以正方形ABCD的边DC向外作等边△DCE,则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
M
A
B
C
D
E
F
O
分析
7. 已知:如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF。
求证:∠AFE=∠AEF。
A
B
C
D
E
F
如图,点E、F在正方形ABCD的边BC、CD上,BE=CF,探索图中AE与BF的关系。
A
B
C
D
E
F
G
你觉得什么样的四边形是正方形呢 ( 判断一个四边形是正方形有哪些方法?)
平行四边形
正方形
一组邻边相等
且一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
平行四边形
正方形
对角线垂直且相等
4、
矩形
6、
对角线垂直
正方形
正方形
菱形
对角线相等
5、
正方形的判定
1、有一组邻边相等,并且有一个角是直角的平行四边形是正方形。
2、一组邻边相等的矩形是正方形。
3、有一个角是直角的菱形是正方形。
4、对角线垂直且相等的平行四边形是正方形。
5、对角线相等的菱形是正方形。
6、对角线垂直的矩形是正方形。
总之,既是矩形又是菱形的四边形是正方形
√
√
√
×
判断题:
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等,且有一个角是直角的四边形
是正方形( )
√
1.不能判定四边形是正方形的是( )
A.对角线互相垂直且相等的四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分且相等的四边形
2、(绵阳)四边形ABCD的对角线相交于点O,能判定它是正方形的条件是( )
A.AB=BC=CD=DA
B.AO=CO,BO=DO,AC⊥BD
C.AC=BD,AC⊥BD且AC、BD互相平分 D.AB=BC,CD=DA
A
C
3.已知四边形ABCD是菱形,则只须补充条件: (用字母表示)就可以判定四边形ABCD是正方形.
4.已知四边形ABCD是矩形,则只须补充条件: (用字母表示)就可以判定四边形ABCD是正方形.
例1:如图,正方形ABCD中,E是对角线BD上一点,过点E作EF⊥ BC,EG⊥ CD,垂足为F、G 。求证:AE=FG。
A
C
B
D
F
G
E
例2.已知:如图,△ABC中.∠ABC=90°,BD是角平分
线,DE⊥AB,DF⊥BC,垂足分别是E、F.
F
A
B
C
D
E
求证:四边形DEBF是正方形.
证明:∵ DE⊥AB,DF⊥BC
∴∠BED=∠BFD=∠ABC=900,
∴四边形DEBF是矩形,
∵ BD平分∠ABC,且 DF⊥BC , DE⊥AB,
∴ DE= DF,
∴四边形DEBF是正方形.
(有一组邻边相等的矩形是正方形)
例3:在正方形ABCD中,点A`,B`,C`,D`分别是AB,BC,CD,DA的中点,四边形A`B`C`D`是正方形吗?为什么?
A
B
C
D
D`
C`
B`
A`
变式训练:正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?
D`
C`
B`
A`
D
C
B
A
变式练习:正方形ABCD中,对角线AC和BD交于点O,点A`,B`,C`,D`分别是AO,BO,CO,DO的中点,判断四边形A`B`C`D`的形状。说明原因
A
B
C
D
D`
C`
B`
A`
O
变式练习:正方形ABCD中,对角线AC和BD交于点O,点A`,B`,C`,D`分别在AC、BD上,且AA`=BB`=CC`=DD`.
判断四边形A`B`C`D`的形状
A
B
D
D`
C`
B`
A`
O
C
例3:(淄博)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
例4、如图,△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3) 当点O运动到何处时,四边形AECF是有可能是正方形?并证明你的结论.
边 角 对 角 线 对 称 性
平 行
四边形
矩 形
菱 形
正方形
几种特殊四边形的性质
对边平行
且相等
对边平行 且相等
对边平行
四边相等
对角相等
邻角互补
四个角
都是直角
对角相等
邻角互补
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
是轴对称图形
对边平行四边相等
四个角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
是轴对称图形
是轴对称图形
不是轴对称图形
正方形
矩形
菱形
平行四边形
有一个角是直角
有一组邻边相等
回顾:特殊的平行四边形
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形叫正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形叫正方形
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形
有一个角是直角的菱形叫做正方形
有一组邻边相等的矩形叫正方形
正方形即是特殊的平行四边形又是特殊的矩形和菱形
平行四边形,矩形,菱形,正方形的关系!
菱形
矩形
平行四边形
正
形
方
正方形具有平行四边形、矩形、菱形的所有性质
正方形有哪些性质?
正方形的性质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形
C
D
\
\
B
\
A
\
正方形对边平行且四条边相等
数学语言:∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
正方形四个角都是直角
数学语言:∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
A
B
C
D
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
1、正方形具有而菱形不一定具有的性质是( )
(A)四条边相等 (B)对角线互相垂直平分
(C)对角线平分一组对角 (D)对角线相等
2、正方形具有而矩形不一定具有的性质是( )
(A)四个角相等 (B)对角线互相垂直平分
(C)对角线相等 (D)对角互补
3、如图:正方形ABCD的周长为15cm,则矩形EFCG的周长
为 cm。
A
B
C
D
E
G
F
D
B
7.5
6.正方形ABCD中,M为AD中点,ME⊥BD于E,MF⊥AC于F,若ME+MF =8cm,则AC=________.
课堂练习
4.已知正方形ABCD中,AC=10,P是AB上一点,PE⊥AC于E,PF⊥BD于F,则PE+PF=______________.
5
30°
16cm
5.以正方形ABCD的边DC向外作等边△DCE,则∠AEB=_____.
P
A
B
C
D
E
F
O
E
A
B
C
D
M
A
B
C
D
E
F
O
分析
7. 已知:如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF。
求证:∠AFE=∠AEF。
A
B
C
D
E
F
如图,点E、F在正方形ABCD的边BC、CD上,BE=CF,探索图中AE与BF的关系。
A
B
C
D
E
F
G
你觉得什么样的四边形是正方形呢 ( 判断一个四边形是正方形有哪些方法?)
平行四边形
正方形
一组邻边相等
且一内角是直角
1、
正方形
菱形
2、
一内角是直角
矩形
3、
一组邻边相等
正方形
平行四边形
正方形
对角线垂直且相等
4、
矩形
6、
对角线垂直
正方形
正方形
菱形
对角线相等
5、
正方形的判定
1、有一组邻边相等,并且有一个角是直角的平行四边形是正方形。
2、一组邻边相等的矩形是正方形。
3、有一个角是直角的菱形是正方形。
4、对角线垂直且相等的平行四边形是正方形。
5、对角线相等的菱形是正方形。
6、对角线垂直的矩形是正方形。
总之,既是矩形又是菱形的四边形是正方形
√
√
√
×
判断题:
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )
(2)对角线互相垂直且相等的四边形是正方形( )
(3)如果一个菱形的对角线相等,那么它一定
是正方形 ( )
(4)如果一个矩形的对角线互相垂直,那么它
一定是正方形 ( )
(5)四条边相等,且有一个角是直角的四边形
是正方形( )
√
1.不能判定四边形是正方形的是( )
A.对角线互相垂直且相等的四边形
B.对角线互相垂直的矩形
C.对角线相等的菱形
D.对角线互相垂直平分且相等的四边形
2、(绵阳)四边形ABCD的对角线相交于点O,能判定它是正方形的条件是( )
A.AB=BC=CD=DA
B.AO=CO,BO=DO,AC⊥BD
C.AC=BD,AC⊥BD且AC、BD互相平分 D.AB=BC,CD=DA
A
C
3.已知四边形ABCD是菱形,则只须补充条件: (用字母表示)就可以判定四边形ABCD是正方形.
4.已知四边形ABCD是矩形,则只须补充条件: (用字母表示)就可以判定四边形ABCD是正方形.
例1:如图,正方形ABCD中,E是对角线BD上一点,过点E作EF⊥ BC,EG⊥ CD,垂足为F、G 。求证:AE=FG。
A
C
B
D
F
G
E
例2.已知:如图,△ABC中.∠ABC=90°,BD是角平分
线,DE⊥AB,DF⊥BC,垂足分别是E、F.
F
A
B
C
D
E
求证:四边形DEBF是正方形.
证明:∵ DE⊥AB,DF⊥BC
∴∠BED=∠BFD=∠ABC=900,
∴四边形DEBF是矩形,
∵ BD平分∠ABC,且 DF⊥BC , DE⊥AB,
∴ DE= DF,
∴四边形DEBF是正方形.
(有一组邻边相等的矩形是正方形)
例3:在正方形ABCD中,点A`,B`,C`,D`分别是AB,BC,CD,DA的中点,四边形A`B`C`D`是正方形吗?为什么?
A
B
C
D
D`
C`
B`
A`
变式训练:正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?
D`
C`
B`
A`
D
C
B
A
变式练习:正方形ABCD中,对角线AC和BD交于点O,点A`,B`,C`,D`分别是AO,BO,CO,DO的中点,判断四边形A`B`C`D`的形状。说明原因
A
B
C
D
D`
C`
B`
A`
O
变式练习:正方形ABCD中,对角线AC和BD交于点O,点A`,B`,C`,D`分别在AC、BD上,且AA`=BB`=CC`=DD`.
判断四边形A`B`C`D`的形状
A
B
D
D`
C`
B`
A`
O
C
例3:(淄博)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
例4、如图,△ABC中,点O是AC边上一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3) 当点O运动到何处时,四边形AECF是有可能是正方形?并证明你的结论.
边 角 对 角 线 对 称 性
平 行
四边形
矩 形
菱 形
正方形
几种特殊四边形的性质
对边平行
且相等
对边平行 且相等
对边平行
四边相等
对角相等
邻角互补
四个角
都是直角
对角相等
邻角互补
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
是轴对称图形
对边平行四边相等
四个角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
是轴对称图形
是轴对称图形
不是轴对称图形
