《数学广角搭配一》(课件)人教版二年级上册数学(共38张PPT)
文档属性
| 名称 | 《数学广角搭配一》(课件)人教版二年级上册数学(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 21:36:41 | ||
图片预览









文档简介
(共38张PPT)
第1课时 排列
8 数学广角——搭配(一)
游戏导入
提示一:老师的年龄是两位数。
游戏:猜年龄。
提示二:由数字1和3组成。
老师的年龄是:
31
探究点 简单的排列问题
探索新知
用1、2和3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
问题:谁能完整地说一说这道题的意思?
探索新知
用1、2和3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
按规律做就不乱了。
我有点儿乱,怎样才能做到不重不漏呢?
1
2
3
1
2
3
探索新知
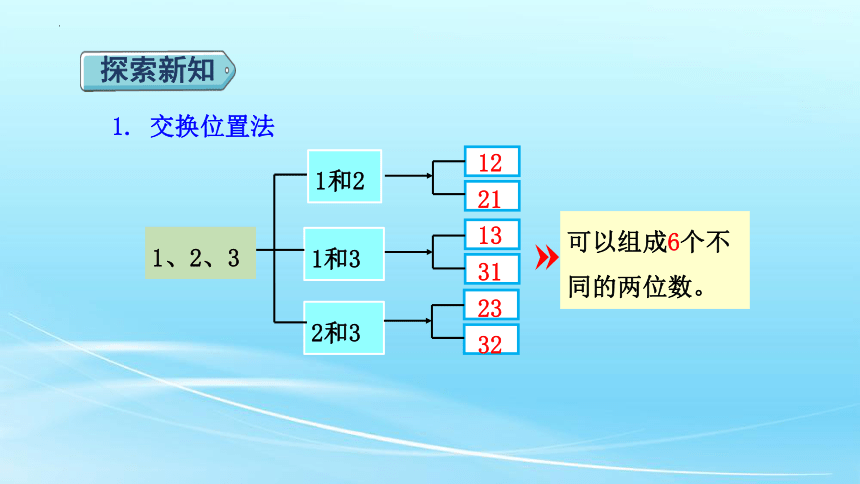
可以组成6个不同的两位数。
1、2、3
1和3
2和3
1和2
12
13
21
31
32
23
1. 交换位置法
探索新知
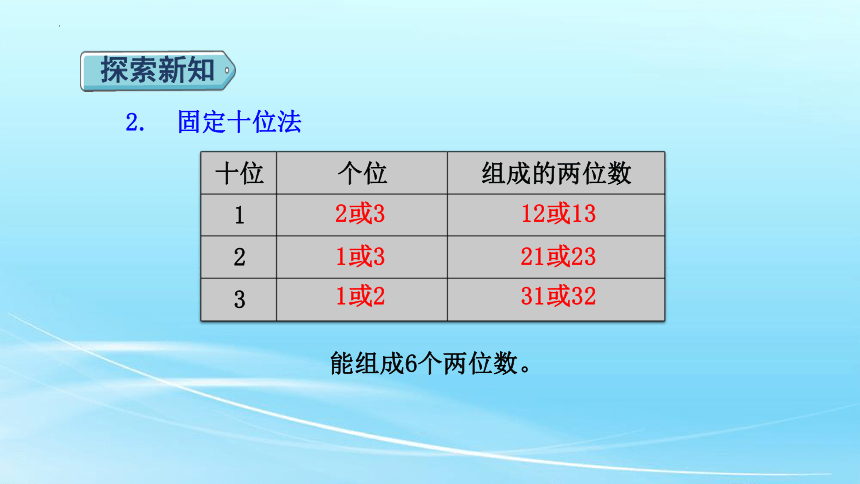
十位 个位 组成的两位数
1
2
3
2或3
1或3
1或2
12或13
21或23
31或32
能组成6个两位数。
2. 固定十位法
探索新知
归纳总结:
解决摆数的问题,关键做到不重复不遗漏,可以用列举的方法,先考虑高位,再考虑低位,有顺序地依次排列,一一列举出所有可能的数。
探索新知
小试牛刀
一共有6种涂色方法。
用 和 3种颜色中,选出两种颜色,给地图上的2个城区涂上不同的颜色,一共有多少种涂色方法?
当堂检测
夯实基础
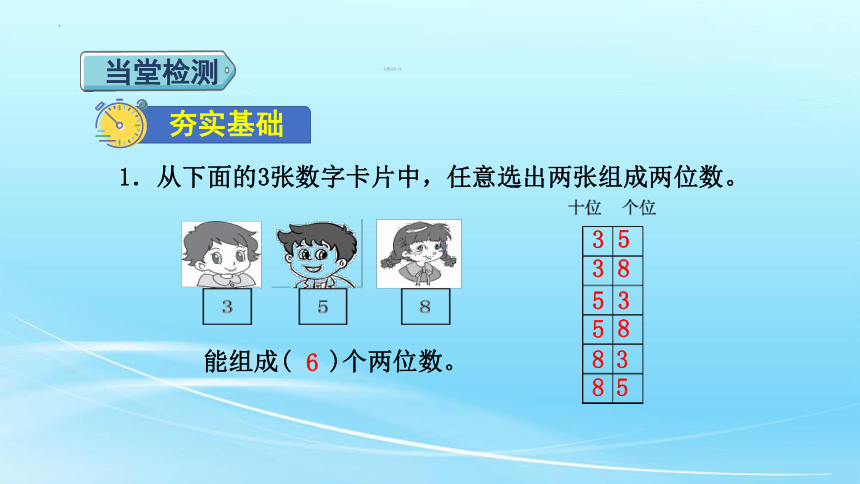
1.从下面的3张数字卡片中,任意选出两张组成两位数。
能组成( )个两位数。
6
3
5
3
8
5
3
5
8
8
3
8
5
当堂检测
2.从下面的4张数字卡片中,任意选出两张组成两位数。
能组成( )个两位数。分别是:_____________________________
_____________________________
16,17,12,61,67,62,
71,76,72,21,26,27
12
当堂检测
易错辨析
3.用下面的3张卡片组成两位数。
能组成( )个大于80的两位数,分别是:_____________________________________
86, 89, 96, 98
4
辨析:三张卡片能组成6个两位数,大于80 的有4个。
当堂检测
4.明明家的电话号码是63493 ,最后3个数是由2、3、4组成的,猜一猜,明明家的电话号码有多少种可能?请你列出后面的3个数 。
6种:
234
243
324
342
423
432
课堂总结
三个不同的数字组成没有重复数字的两位数时,让每个数字(0除外)先作十位数,然后其余两个数字依次和它组合。也可以将这三个数字搭配成3组,然后交换个位和十位上的数字进行组合。
简单的排列问题:
作 业 请完成教材练习二十四第1题、 第2题。
课后作业
知识点
与数字有关的排列问题
1.从这三张卡片中,任意选
出两张组成两位数。
首位确定
一共能组成( )个不同的两位数。
2 2 5 5 7 7
5 7 2 7 2 5
6
(部分答案不唯一)
2.梦梦和爸爸、妈妈一起外出游玩并拍照留念。他们一家站成一排拍照,一共有几种不同的排法?请按规律排一排。
提升点 1
运用首位确定法或交换位置法解决拍照的不同排法
一共有6种不同的排法,分别是爸爸、
妈妈、梦梦;爸爸、梦梦、妈妈;妈妈、爸爸、梦梦;妈妈、梦梦、爸爸;梦梦、爸爸、妈妈;梦梦、妈妈、爸爸。
3.(易错题)典典从下面三种玩具中选2 件,分别送给蓝蓝、同同各1 件,一共有多少种送法?
提升点 2
运用首位确定法或交换位置法解决送礼物的数学问题
一共有6种送法。
辨析:这是一个排列问题,先确定一种玩具送给蓝蓝,同同就有2种送法,三种玩具就有3个2种送法,即有6种送法。如下表:
蓝蓝 布娃娃 布娃娃 玩具车 玩具车 玩具熊 玩具熊
同同 玩具车 玩具熊 布娃娃 玩具熊 布娃娃 玩具车
第2课时 组合
8 数学广角——搭配(一)
复习导入
有3个数5、7、9,任意选取其中2个组成两位数,一共能组成几个?
5
7
5
9
7
5
7
9
9
5
9
7
一共能组成6个。
探究点 简单的组合问题
探索新知
从5、7、9这三个数中,任意选取其中2个求和,得数有几种可能?
探索新知
加数 加数 和
12
14
12
16
14
16
得数有12、14 、16三种可能。
5
5
7
7
9
9
7
9
5
9
5
7
两个数的和与顺序没有关系!
1.列表法
探索新知
5 7 9
12
16
14
得数有三种可能。
2.连线法
探索新知
用两个数字组数,只要把这两个数字调换位置,组成的两个数就不同。
两个数的和,无论两个数怎样调换位置,和都不变。
排列与事物的顺序有关,组合与事物的顺序无关。
组合与排列的区别是什么?
探索新知
归纳总结:
组合与排列不同,它与顺序无关,可利用列表法或连线法来解决组合的问题。
探索新知
小试牛刀
每两个人握1次手,3人一共握几次手?
3人一共握3次手。
当堂检测
夯实基础
1.
来自天津、北京、广州的三个人互通电话,每两个人通一次电话,一共要通( )次电话。写一写。(写序号)
3
①②, ①③, ②③
当堂检测
2.每两个小朋友握1次手,4个小朋友一共要握几次手?写一写。(写序号)
握6次手,分别是①②,①③,①④,②③,②④,③④。
当堂检测
3.任选两个球,一共有多少种不同的选法?
可以通过连线来解决。
一共有3种不同的选法。
当堂检测
易错辨析
4.下面有3本书,明明想买其中的两本,有多少种买法?
答:有3种买法。
辨析:混淆排列和组合。买的两本书没有顺序,是组合问题。
课堂总结
在解决组合问题时,只要按照一定的规律去思考,就可以不重复、不遗漏地把所有的可能找出来。与排列不同,组合与顺序没有关系。
简单的组合问题:
作 业 请完成教材练习二十四第3题、 第4题。
课后作业
乘数 乘数 积
知识点
与数字有关的组合问题
1.从 3 个数中任意选出2 个数求出积,得数有几种可能?
4 6 24
列表法:
4 8 32
6 8 48
得数有3种可能。
连线
(答案不唯一)
2.有几种不同的选法?(连一连)
有6种不同的选法。
提升点 1
用连线法解决组合中的“连线”问题
3.华华想买一本15 元的书,可以怎样付钱?照样子完成下表。
提升点 2
用列表法解决组合中的“付钱”问题
辨析:注意思考要有顺序。
10元/张 5元/张 1元/张
第一种 1 1
第二种 1 5
第三种 3
第四种 2 5
第1课时 排列
8 数学广角——搭配(一)
游戏导入
提示一:老师的年龄是两位数。
游戏:猜年龄。
提示二:由数字1和3组成。
老师的年龄是:
31
探究点 简单的排列问题
探索新知
用1、2和3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
问题:谁能完整地说一说这道题的意思?
探索新知
用1、2和3组成两位数,每个两位数的十位数和个位数不能一样,能组成几个两位数?
按规律做就不乱了。
我有点儿乱,怎样才能做到不重不漏呢?
1
2
3
1
2
3
探索新知
可以组成6个不同的两位数。
1、2、3
1和3
2和3
1和2
12
13
21
31
32
23
1. 交换位置法
探索新知
十位 个位 组成的两位数
1
2
3
2或3
1或3
1或2
12或13
21或23
31或32
能组成6个两位数。
2. 固定十位法
探索新知
归纳总结:
解决摆数的问题,关键做到不重复不遗漏,可以用列举的方法,先考虑高位,再考虑低位,有顺序地依次排列,一一列举出所有可能的数。
探索新知
小试牛刀
一共有6种涂色方法。
用 和 3种颜色中,选出两种颜色,给地图上的2个城区涂上不同的颜色,一共有多少种涂色方法?
当堂检测
夯实基础
1.从下面的3张数字卡片中,任意选出两张组成两位数。
能组成( )个两位数。
6
3
5
3
8
5
3
5
8
8
3
8
5
当堂检测
2.从下面的4张数字卡片中,任意选出两张组成两位数。
能组成( )个两位数。分别是:_____________________________
_____________________________
16,17,12,61,67,62,
71,76,72,21,26,27
12
当堂检测
易错辨析
3.用下面的3张卡片组成两位数。
能组成( )个大于80的两位数,分别是:_____________________________________
86, 89, 96, 98
4
辨析:三张卡片能组成6个两位数,大于80 的有4个。
当堂检测
4.明明家的电话号码是63493 ,最后3个数是由2、3、4组成的,猜一猜,明明家的电话号码有多少种可能?请你列出后面的3个数 。
6种:
234
243
324
342
423
432
课堂总结
三个不同的数字组成没有重复数字的两位数时,让每个数字(0除外)先作十位数,然后其余两个数字依次和它组合。也可以将这三个数字搭配成3组,然后交换个位和十位上的数字进行组合。
简单的排列问题:
作 业 请完成教材练习二十四第1题、 第2题。
课后作业
知识点
与数字有关的排列问题
1.从这三张卡片中,任意选
出两张组成两位数。
首位确定
一共能组成( )个不同的两位数。
2 2 5 5 7 7
5 7 2 7 2 5
6
(部分答案不唯一)
2.梦梦和爸爸、妈妈一起外出游玩并拍照留念。他们一家站成一排拍照,一共有几种不同的排法?请按规律排一排。
提升点 1
运用首位确定法或交换位置法解决拍照的不同排法
一共有6种不同的排法,分别是爸爸、
妈妈、梦梦;爸爸、梦梦、妈妈;妈妈、爸爸、梦梦;妈妈、梦梦、爸爸;梦梦、爸爸、妈妈;梦梦、妈妈、爸爸。
3.(易错题)典典从下面三种玩具中选2 件,分别送给蓝蓝、同同各1 件,一共有多少种送法?
提升点 2
运用首位确定法或交换位置法解决送礼物的数学问题
一共有6种送法。
辨析:这是一个排列问题,先确定一种玩具送给蓝蓝,同同就有2种送法,三种玩具就有3个2种送法,即有6种送法。如下表:
蓝蓝 布娃娃 布娃娃 玩具车 玩具车 玩具熊 玩具熊
同同 玩具车 玩具熊 布娃娃 玩具熊 布娃娃 玩具车
第2课时 组合
8 数学广角——搭配(一)
复习导入
有3个数5、7、9,任意选取其中2个组成两位数,一共能组成几个?
5
7
5
9
7
5
7
9
9
5
9
7
一共能组成6个。
探究点 简单的组合问题
探索新知
从5、7、9这三个数中,任意选取其中2个求和,得数有几种可能?
探索新知
加数 加数 和
12
14
12
16
14
16
得数有12、14 、16三种可能。
5
5
7
7
9
9
7
9
5
9
5
7
两个数的和与顺序没有关系!
1.列表法
探索新知
5 7 9
12
16
14
得数有三种可能。
2.连线法
探索新知
用两个数字组数,只要把这两个数字调换位置,组成的两个数就不同。
两个数的和,无论两个数怎样调换位置,和都不变。
排列与事物的顺序有关,组合与事物的顺序无关。
组合与排列的区别是什么?
探索新知
归纳总结:
组合与排列不同,它与顺序无关,可利用列表法或连线法来解决组合的问题。
探索新知
小试牛刀
每两个人握1次手,3人一共握几次手?
3人一共握3次手。
当堂检测
夯实基础
1.
来自天津、北京、广州的三个人互通电话,每两个人通一次电话,一共要通( )次电话。写一写。(写序号)
3
①②, ①③, ②③
当堂检测
2.每两个小朋友握1次手,4个小朋友一共要握几次手?写一写。(写序号)
握6次手,分别是①②,①③,①④,②③,②④,③④。
当堂检测
3.任选两个球,一共有多少种不同的选法?
可以通过连线来解决。
一共有3种不同的选法。
当堂检测
易错辨析
4.下面有3本书,明明想买其中的两本,有多少种买法?
答:有3种买法。
辨析:混淆排列和组合。买的两本书没有顺序,是组合问题。
课堂总结
在解决组合问题时,只要按照一定的规律去思考,就可以不重复、不遗漏地把所有的可能找出来。与排列不同,组合与顺序没有关系。
简单的组合问题:
作 业 请完成教材练习二十四第3题、 第4题。
课后作业
乘数 乘数 积
知识点
与数字有关的组合问题
1.从 3 个数中任意选出2 个数求出积,得数有几种可能?
4 6 24
列表法:
4 8 32
6 8 48
得数有3种可能。
连线
(答案不唯一)
2.有几种不同的选法?(连一连)
有6种不同的选法。
提升点 1
用连线法解决组合中的“连线”问题
3.华华想买一本15 元的书,可以怎样付钱?照样子完成下表。
提升点 2
用列表法解决组合中的“付钱”问题
辨析:注意思考要有顺序。
10元/张 5元/张 1元/张
第一种 1 1
第二种 1 5
第三种 3
第四种 2 5
