福建省福州市闽江学院附属中学2021-2022学年高三上学期开学考试数学试卷(含答案)
文档属性
| 名称 | 福建省福州市闽江学院附属中学2021-2022学年高三上学期开学考试数学试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 00:00:00 | ||
图片预览





文档简介
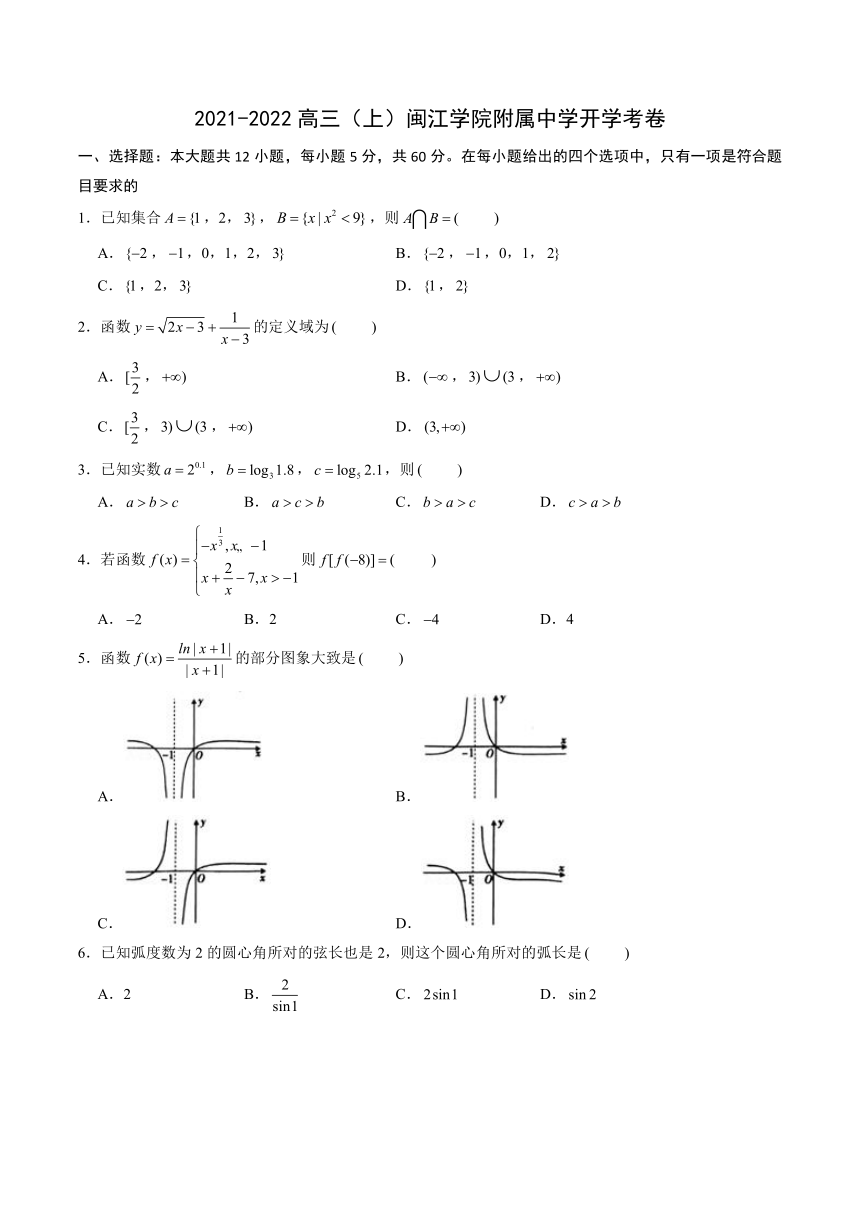
2021-2022高三(上)闽江学院附属中学开学考卷
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知集合,2,,,则
A.,,0,1,2, B.,,0,1,
C.,2, D.,
2.函数的定义域为
A., B.,,
C.,, D.
3.已知实数,,,则
A. B. C. D.
4.若函数则
A. B.2 C. D.4
5.函数的部分图象大致是
A. B.
C. D.
6.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是
A.2 B. C. D.
7.已知,则的值等于
A. B. C. D.
8.设函数是奇函数的导函数,.当时,,则使得成立的的取值范围是
A.,, B.,,
C.,, D.,,
9.下列函数中为奇函数的是
A. B.
C. D.
二.多选题(共3小题)
10.下列命题中是假命题的有
A.有四个实数解
B.设、、是实数,若二次方程无实根,则
C.若,则
D.若,则函数的最小值为2
11.已知函数,则下列结论正确的是
A.的图象关于直线对称
B.的图象关于点对称
C.在区间上单调递增
D.在区间上有两个零点
12.关于函数,下列叙述正确的是
A.是偶函数 B.在区间,单调递增
C.的最大值为2 D.在,有4个零点
三.填空题(共3小题)
13.求值:__________.
14.已知点在第三象限,则角的终边在第__________象限.
15.如图所示,是可导函数,直线是曲线在处的切线,若,则(1)__________.
16.已知偶函数在区间,上单调递增,且满足,给出下列判断:
①;②在,上是增函数;③的图象关与直线对称;④函数在处取得最小值;⑤函数没有最大值,其中判断正确的序号是__________.
四.解答题(共6小题)
17.已知集合,.
(1)若,求;
(2)若,,求的取值范围.
18.已知.
(Ⅰ)求的最小正周期及单调递减区间;
(Ⅱ)求函数在区间上的最大值和最小值.
19.的内角,,的对边分别为,,,已知.
(Ⅰ)求;
(Ⅱ)若,的中垂线交于点,求的长.
20.已知函数,,的部分图象如图所示.
(Ⅰ)求函数的解析式;
(Ⅱ)将函数的图象向左平移个单位后,再将得到的图象上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数的图象,求函数的单调递减区间.
21.已知函数,曲线在处的切线方程为.
(Ⅰ)求函数的解析式;
(Ⅱ)求的极值.
22.某市为提高市民的健康水平,拟在半径为200米的半圆形区域内修建一个健身广场,该健身广场(如图所示的阴影部分)分休闲健身和儿童活动两个功能区,图中矩形区域是休闲健身区,以为底边的等腰三角形区域是儿童活动区,,,三点在圆弧上,中点恰好为圆心.设,健身广场的面积为.
(1)求出关于的函数解析式;
(2)当角取何值时,健身广场的面积最大?
2021-2022高三(上)闽江学院附属中学开学考卷
参考答案与试题解析
一.选择题(共10小题)
1.已知集合,2,,,则
A.,,0,1,2, B.,,0,1,
C.,2, D.,
【解答】解:集合,2,,,
,.
故选:.
2.函数的定义域为
A., B.,,
C.,, D.
【解答】解:函数,
,
解得且;
函数的定义域为,,.
故选:.
3.已知实数,,,则
A. B. C. D.
【解答】解:因为,,
,
所以,
故选:.
4.若函数则
A. B.2 C. D.4
【解答】解:函数
,
(2).
故选:.
5.函数的部分图象大致是
A. B.
C. D.
【解答】解:函数的定义域为,
当时,,排除,
且函数关于对称,排除,
故选:.
6.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是
A.2 B. C. D.
【解答】解:如图:,过点0作,为垂足,并延长交于,
,,
中,,
从而弧长为,
故选:.
7.已知,则的值等于
A. B. C. D.
【解答】解:因为与互余,
所以,
故选:.
8.设函数是奇函数的导函数,.当时,,则使得成立的的取值范围是
A.,, B.,,
C.,, D.,,
【解答】解:由,可得,
令,则,
故在上单调递增,
因为,
所以,
又因为为奇函数,
所以为奇函数,
所以(1),且在区间上,单调递增,
所以使得,即成立的的取值范围是,,,
故选:..
二.多选题(共3小题)
9.下列函数中,奇函数有
A. B.
C. D.
【解答】解:显然ABD满足题意,
故选:BD.
10.下列命题中是假命题的有
A.有四个实数解
B.设、、是实数,若二次方程无实根,则
C.若,则
D.若,则函数的最小值为2
【解答】解:则或,故方程只有两个实数解,故是假命题;
设、、是实数,若二次方程无实根,则,则,则,可以推出,故是真命题;
若,则且,可推出,故是真命题;
若,则函数的最小值为,此时,故是假命题.
故选:.
11.已知函数,则下列结论正确的是
A.的图象关于直线对称
B.的图象关于点对称
C.在区间上单调递增
D.在区间上有两个零点
【解答】解:选项,,取到最大值,选项说法正确.
选项,的图象为向上平移1个单位,故对称中心的纵坐标为1,选项说法错误.
选项,当时,,又在上单调递增,所以单调递增,选项说法正确.
选项,令,得,即,故在区间上没有零点,选项说法错误.
故选:.
12.关于函数,下列叙述正确的是
A.是偶函数 B.在区间,单调递增
C.的最大值为2 D.在,有4个零点
【解答】解:,且的定义域为,
是偶函数,故选项正确,
当时,,在区间上单调递减,故选项错误,
函数是偶函数,
考虑的情况,即可求解,
当时,,
的最大值为2,故选项正确.
函数是偶函数,
只需考虑,上的零点个数,
当,时,
,故在,上有2个零点,分别为,,
在,有三个零点,分别为,,,故选项错误.
故选:.
三.填空题(共3小题)
13.求值: 0 .
【解答】解:根据题意,原式,
故答案为:0.
14.已知点在第三象限,则角的终边在第__________象限.
【解答】解:在第三象限,
,
由,得在第二、四象限,
由,得在第二、三象限
在第二象限.
15.如图所示,是可导函数,直线是曲线在处的切线,若,则(1) 1 .
【解答】解:直线是曲线在处的切线,
点为切点,故(1),(1),
解得,故(1),(1),
由可得,
(1)(1)(1),
故答案为:1.
16.已知偶函数在区间,上单调递增,且满足,给出下列判断:
①;②在,上是增函数;③的图象关与直线对称;④函数在处取得最小值;⑤函数没有最大值,其中判断正确的序号是 ①④ .
【解答】解:由得到,所以,所以函数的周期是4.
当时,(1)(1),所以(1),因为(5)(1),
(1)所以①正确;
因为在区间,上单调递增,,所以函数在区间,单调递减,所以②不正确;
因为是偶函数,所以对称轴为,所以③不正确.
因为偶函数在区间,上单调递增,,所以函数在区间,单调递减,,单调递增,所以在处取得最小值,故④正确;
显然函数的最大值为故⑤错误;
故答案为:①④.
四.解答题(共6小题)
17.已知集合,.
(1)若,求;
(2)若,,求的取值范围.
【解答】解:(1)由,解得,集合;
当时,可化为,即,
解得,集合,
;
(2),,.
,
,
.
18.已知.
(Ⅰ)求的最小正周期及单调递减区间;
(Ⅱ)求函数在区间上的最大值和最小值.
【解答】解:(Ⅰ).
故函数的最小值正周期为.
令:,
解得,
故函数的单调递减区间为:.
(Ⅱ)由于,
所以,
所以,
整理得:
即,,即当时,函数取得最小值为0,当时,函数取得最大值为3.
19.的内角,,的对边分别为,,,已知.
(Ⅰ)求;
(Ⅱ)若,的中垂线交于点,求的长.
【解答】(本题满分为12分)
解:(Ⅰ)在中,,
由正弦定理知,(2分)
,
,于是,即(4分)
.(6分)
(Ⅱ)由(Ⅰ)和余弦定理知,,
,(8分)
,(10分)
设的中垂线交于点,
在中,,
.(12分)
20.已知函数,,的部分图象如图所示.
(Ⅰ)求函数的解析式;
(Ⅱ)将函数的图象向左平移个单位后,再将得到的图象上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数的图象,求函数的单调递减区间.
【解答】解:(Ⅰ)由图象可知,,,
所以,则,
又,
又,
则,
所以;
(Ⅱ)由题意可得,函数,
故,
令,
解得,
所以函数的单调递减区间为.
21.已知函数,曲线在处的切线方程为.
(Ⅰ)求函数的解析式;
(Ⅱ)求的极值.
【分析】(Ⅰ)根据导数的几何意义,及切点在切线也在曲线上,解得,的值,进而得出解析式.
(Ⅱ)在(Ⅰ)的基础上求导数,先分析单调性,再求极值即可.
【解答】解:(Ⅰ),
则,
又因为曲线在处的切线方程为,
所以,
因为切点在切线上也在曲线上,
所以,所以,,
所以的解析式为.
(Ⅱ)定义域为,,
令,得或,
所以在,上,,单调递增,
在上,,单调递减,
所以,
.
22.某市为提高市民的健康水平,拟在半径为200米的半圆形区域内修建一个健身广场,该健身广场(如图所示的阴影部分)分休闲健身和儿童活动两个功能区,图中矩形区域是休闲健身区,以为底边的等腰三角形区域是儿童活动区,,,三点在圆弧上,中点恰好为圆心.设,健身广场的面积为.
(1)求出关于的函数解析式;
(2)当角取何值时,健身广场的面积最大?
【解答】解:(1)由已知得,,,
等腰三角形底边上的高为,
,
;
(2)设,
则
.
由,得,由,得,
在上单调递增,在,上单调递减,
时,.
.
即时,健身广场面积最大,最大值为.
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知集合,2,,,则
A.,,0,1,2, B.,,0,1,
C.,2, D.,
2.函数的定义域为
A., B.,,
C.,, D.
3.已知实数,,,则
A. B. C. D.
4.若函数则
A. B.2 C. D.4
5.函数的部分图象大致是
A. B.
C. D.
6.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是
A.2 B. C. D.
7.已知,则的值等于
A. B. C. D.
8.设函数是奇函数的导函数,.当时,,则使得成立的的取值范围是
A.,, B.,,
C.,, D.,,
9.下列函数中为奇函数的是
A. B.
C. D.
二.多选题(共3小题)
10.下列命题中是假命题的有
A.有四个实数解
B.设、、是实数,若二次方程无实根,则
C.若,则
D.若,则函数的最小值为2
11.已知函数,则下列结论正确的是
A.的图象关于直线对称
B.的图象关于点对称
C.在区间上单调递增
D.在区间上有两个零点
12.关于函数,下列叙述正确的是
A.是偶函数 B.在区间,单调递增
C.的最大值为2 D.在,有4个零点
三.填空题(共3小题)
13.求值:__________.
14.已知点在第三象限,则角的终边在第__________象限.
15.如图所示,是可导函数,直线是曲线在处的切线,若,则(1)__________.
16.已知偶函数在区间,上单调递增,且满足,给出下列判断:
①;②在,上是增函数;③的图象关与直线对称;④函数在处取得最小值;⑤函数没有最大值,其中判断正确的序号是__________.
四.解答题(共6小题)
17.已知集合,.
(1)若,求;
(2)若,,求的取值范围.
18.已知.
(Ⅰ)求的最小正周期及单调递减区间;
(Ⅱ)求函数在区间上的最大值和最小值.
19.的内角,,的对边分别为,,,已知.
(Ⅰ)求;
(Ⅱ)若,的中垂线交于点,求的长.
20.已知函数,,的部分图象如图所示.
(Ⅰ)求函数的解析式;
(Ⅱ)将函数的图象向左平移个单位后,再将得到的图象上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数的图象,求函数的单调递减区间.
21.已知函数,曲线在处的切线方程为.
(Ⅰ)求函数的解析式;
(Ⅱ)求的极值.
22.某市为提高市民的健康水平,拟在半径为200米的半圆形区域内修建一个健身广场,该健身广场(如图所示的阴影部分)分休闲健身和儿童活动两个功能区,图中矩形区域是休闲健身区,以为底边的等腰三角形区域是儿童活动区,,,三点在圆弧上,中点恰好为圆心.设,健身广场的面积为.
(1)求出关于的函数解析式;
(2)当角取何值时,健身广场的面积最大?
2021-2022高三(上)闽江学院附属中学开学考卷
参考答案与试题解析
一.选择题(共10小题)
1.已知集合,2,,,则
A.,,0,1,2, B.,,0,1,
C.,2, D.,
【解答】解:集合,2,,,
,.
故选:.
2.函数的定义域为
A., B.,,
C.,, D.
【解答】解:函数,
,
解得且;
函数的定义域为,,.
故选:.
3.已知实数,,,则
A. B. C. D.
【解答】解:因为,,
,
所以,
故选:.
4.若函数则
A. B.2 C. D.4
【解答】解:函数
,
(2).
故选:.
5.函数的部分图象大致是
A. B.
C. D.
【解答】解:函数的定义域为,
当时,,排除,
且函数关于对称,排除,
故选:.
6.已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是
A.2 B. C. D.
【解答】解:如图:,过点0作,为垂足,并延长交于,
,,
中,,
从而弧长为,
故选:.
7.已知,则的值等于
A. B. C. D.
【解答】解:因为与互余,
所以,
故选:.
8.设函数是奇函数的导函数,.当时,,则使得成立的的取值范围是
A.,, B.,,
C.,, D.,,
【解答】解:由,可得,
令,则,
故在上单调递增,
因为,
所以,
又因为为奇函数,
所以为奇函数,
所以(1),且在区间上,单调递增,
所以使得,即成立的的取值范围是,,,
故选:..
二.多选题(共3小题)
9.下列函数中,奇函数有
A. B.
C. D.
【解答】解:显然ABD满足题意,
故选:BD.
10.下列命题中是假命题的有
A.有四个实数解
B.设、、是实数,若二次方程无实根,则
C.若,则
D.若,则函数的最小值为2
【解答】解:则或,故方程只有两个实数解,故是假命题;
设、、是实数,若二次方程无实根,则,则,则,可以推出,故是真命题;
若,则且,可推出,故是真命题;
若,则函数的最小值为,此时,故是假命题.
故选:.
11.已知函数,则下列结论正确的是
A.的图象关于直线对称
B.的图象关于点对称
C.在区间上单调递增
D.在区间上有两个零点
【解答】解:选项,,取到最大值,选项说法正确.
选项,的图象为向上平移1个单位,故对称中心的纵坐标为1,选项说法错误.
选项,当时,,又在上单调递增,所以单调递增,选项说法正确.
选项,令,得,即,故在区间上没有零点,选项说法错误.
故选:.
12.关于函数,下列叙述正确的是
A.是偶函数 B.在区间,单调递增
C.的最大值为2 D.在,有4个零点
【解答】解:,且的定义域为,
是偶函数,故选项正确,
当时,,在区间上单调递减,故选项错误,
函数是偶函数,
考虑的情况,即可求解,
当时,,
的最大值为2,故选项正确.
函数是偶函数,
只需考虑,上的零点个数,
当,时,
,故在,上有2个零点,分别为,,
在,有三个零点,分别为,,,故选项错误.
故选:.
三.填空题(共3小题)
13.求值: 0 .
【解答】解:根据题意,原式,
故答案为:0.
14.已知点在第三象限,则角的终边在第__________象限.
【解答】解:在第三象限,
,
由,得在第二、四象限,
由,得在第二、三象限
在第二象限.
15.如图所示,是可导函数,直线是曲线在处的切线,若,则(1) 1 .
【解答】解:直线是曲线在处的切线,
点为切点,故(1),(1),
解得,故(1),(1),
由可得,
(1)(1)(1),
故答案为:1.
16.已知偶函数在区间,上单调递增,且满足,给出下列判断:
①;②在,上是增函数;③的图象关与直线对称;④函数在处取得最小值;⑤函数没有最大值,其中判断正确的序号是 ①④ .
【解答】解:由得到,所以,所以函数的周期是4.
当时,(1)(1),所以(1),因为(5)(1),
(1)所以①正确;
因为在区间,上单调递增,,所以函数在区间,单调递减,所以②不正确;
因为是偶函数,所以对称轴为,所以③不正确.
因为偶函数在区间,上单调递增,,所以函数在区间,单调递减,,单调递增,所以在处取得最小值,故④正确;
显然函数的最大值为故⑤错误;
故答案为:①④.
四.解答题(共6小题)
17.已知集合,.
(1)若,求;
(2)若,,求的取值范围.
【解答】解:(1)由,解得,集合;
当时,可化为,即,
解得,集合,
;
(2),,.
,
,
.
18.已知.
(Ⅰ)求的最小正周期及单调递减区间;
(Ⅱ)求函数在区间上的最大值和最小值.
【解答】解:(Ⅰ).
故函数的最小值正周期为.
令:,
解得,
故函数的单调递减区间为:.
(Ⅱ)由于,
所以,
所以,
整理得:
即,,即当时,函数取得最小值为0,当时,函数取得最大值为3.
19.的内角,,的对边分别为,,,已知.
(Ⅰ)求;
(Ⅱ)若,的中垂线交于点,求的长.
【解答】(本题满分为12分)
解:(Ⅰ)在中,,
由正弦定理知,(2分)
,
,于是,即(4分)
.(6分)
(Ⅱ)由(Ⅰ)和余弦定理知,,
,(8分)
,(10分)
设的中垂线交于点,
在中,,
.(12分)
20.已知函数,,的部分图象如图所示.
(Ⅰ)求函数的解析式;
(Ⅱ)将函数的图象向左平移个单位后,再将得到的图象上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数的图象,求函数的单调递减区间.
【解答】解:(Ⅰ)由图象可知,,,
所以,则,
又,
又,
则,
所以;
(Ⅱ)由题意可得,函数,
故,
令,
解得,
所以函数的单调递减区间为.
21.已知函数,曲线在处的切线方程为.
(Ⅰ)求函数的解析式;
(Ⅱ)求的极值.
【分析】(Ⅰ)根据导数的几何意义,及切点在切线也在曲线上,解得,的值,进而得出解析式.
(Ⅱ)在(Ⅰ)的基础上求导数,先分析单调性,再求极值即可.
【解答】解:(Ⅰ),
则,
又因为曲线在处的切线方程为,
所以,
因为切点在切线上也在曲线上,
所以,所以,,
所以的解析式为.
(Ⅱ)定义域为,,
令,得或,
所以在,上,,单调递增,
在上,,单调递减,
所以,
.
22.某市为提高市民的健康水平,拟在半径为200米的半圆形区域内修建一个健身广场,该健身广场(如图所示的阴影部分)分休闲健身和儿童活动两个功能区,图中矩形区域是休闲健身区,以为底边的等腰三角形区域是儿童活动区,,,三点在圆弧上,中点恰好为圆心.设,健身广场的面积为.
(1)求出关于的函数解析式;
(2)当角取何值时,健身广场的面积最大?
【解答】解:(1)由已知得,,,
等腰三角形底边上的高为,
,
;
(2)设,
则
.
由,得,由,得,
在上单调递增,在,上单调递减,
时,.
.
即时,健身广场面积最大,最大值为.
同课章节目录
