湖南省邵阳市第二高级中学校2022-2023学年高二上学期9月入学考试数学试题(PDF版含解析)
文档属性
| 名称 | 湖南省邵阳市第二高级中学校2022-2023学年高二上学期9月入学考试数学试题(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-22 22:05:03 | ||
图片预览



文档简介
2022-2023 学年度邵阳市第二中学高中数学试卷
高二一期入学试卷
考试分值:150 分;考试时间:120 分钟;命题人:
第 I卷(选择题)
一.选择题:本大题共 8 小题,每小题 5分,共 40 分,在每个小题给出的 4个选项中,只有
一项是符合题目要求的.
1.若集合M {x∣ x 4}, N {x∣3x 1},则M N ( )
1 A. x 0 x 2 B. x x 2 C. 1 x 3 x 16 D. x x 16
3 3
2.若复数 z满足 i z 3 4i ,则 z ( )
A.1 B.5 C.7 D.25
3.已知向量a (3, 4),b (1,0),c a tb,若 a,c b,c ,则 t ( )
A. 6 B. 5 C.5 D.6
4.已知正三棱锥P ABC的六条棱长均为 6,S是 ABC及其内部的点构成的集合.设
集合T Q S PQ 5 ,则 T表示的区域的面积为( )
3
A. B. C.2 D.3
4
5.如图,在棱长为 2 的正方体 ABCD A1B1C1D1 中,A1B1 的中点是 P,过点 A1作与截面
PBC1平行的截面,则该截面的面积为( )
A.2 2 B.2 3 C.2 6 D.4
6.在 ABC中, AC 3,BC 4, C 90 .P为 ABC所在平面内的动点,且 PC 1,
则PA PB的取值范围是( )
A.[ 5,3] B.[ 3,5] C.[ 6,4] D.[ 4,6]
1
7.一个电路如图所示,A,B,C,D,E,F 为 6 个开关,其闭合的概率为 ,且是相
2
互独立的,则灯亮的概率是( )
试卷第 1 页,共 5 页
1 55 1 1
A. B. C. D.
64 64 8 16
8.设函数 f x 的定义域为 R, f x 1 为奇函数, f x 2 为偶函数,当 x 1,2 时,
9
f (x) ax2 b.若 f 0 f 3 6,则 f ( )
2
9 3 7 5
A. B. C. D.
4 2 4 2
二、多选题(4 个小题每个题 5分共计 20 分,在每个小题给出的四个选项中,有多项符
合题目要求。全部选对得 5分,部分对的得 2分,有选错的得 0分。)
9.已知事件A , B,且P A 0.5,P B 0.2,则下列结论正确的是( )
A.如果B A,那么P A B 0.2,P AB 0.5
B.如果A 与 B互斥,那么P A B 0.7,P AB 0
C.如果A 与 B相互独立,那么P A B 0.7,P AB 0
D.如果A 与 B相互独立,那么 P AB 0.4 ,P AB 0.4
10.在 ABC中,角A , B,C所对的边分别为a,b,c,已知
b c : c a : a b 4 :5 : 6 ,则下列结论正确的是( )
A.sin A : sinB : sinC 7 :5 :3
B.CA AB 0
C.若 c 6 ,则 ABC的面积是 15
D.若b c 8,则 ABC 7 3外接圆半径是
3
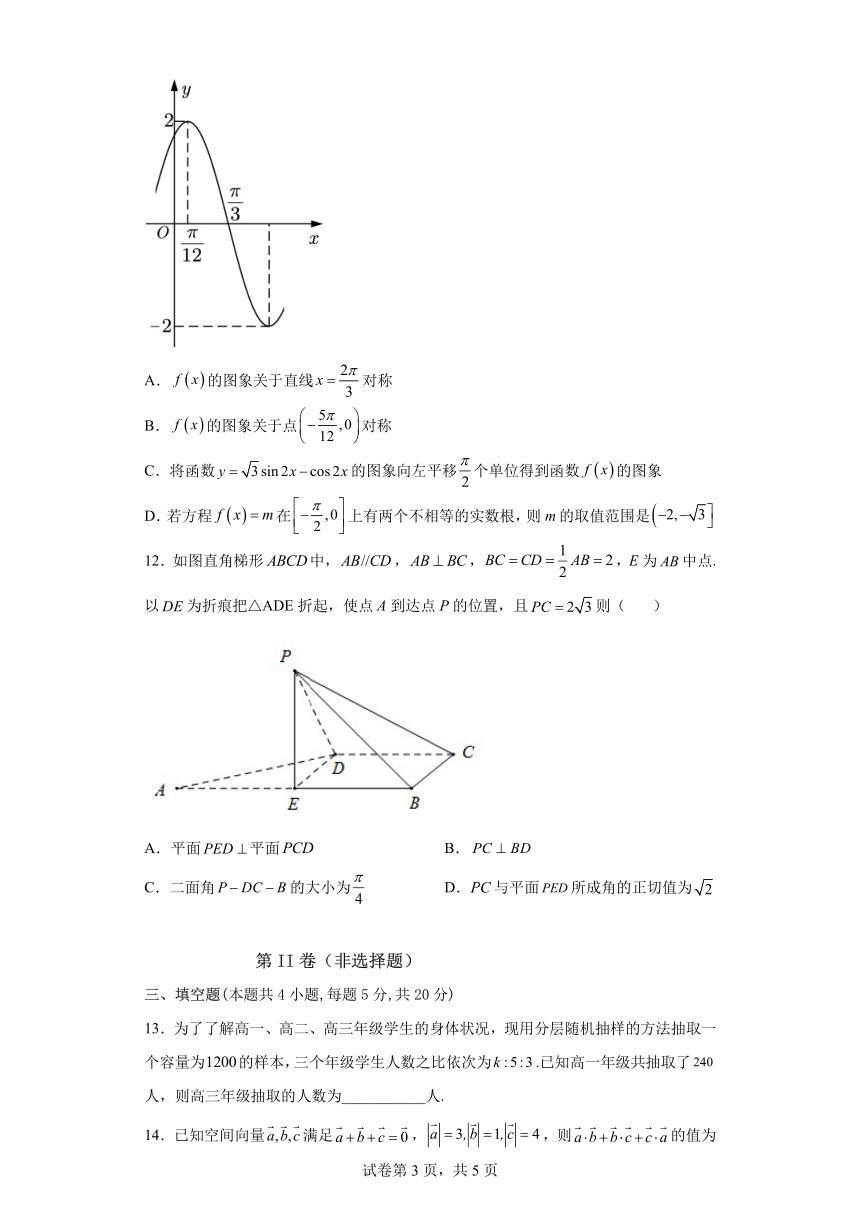
11.已知函数 f (x) Asin( x )
, A
0, 0, 部分图象如图所示,下列说法
2
不正确的是( )
试卷第 2 页,共 5 页
2 A. f x 的图象关于直线 x 对称
3
B. f x 5 的图象关于点 , 0 对称
12
C.将函数 y 3 sin 2x cos 2x的图象向左平移 个单位得到函数 f x 的图象
2
D.若方程 f x m 在 , 0 上有两个不相等的实数根,则 m的取值范围是 2, 3 2
1
12.如图直角梯形 ABCD中,AB//CD,AB BC,BC CD AB 2,E为 AB中点.
2
以DE 为折痕把△ADE 折起,使点 A到达点 P的位置,且PC 2 3 则( )
A.平面PED 平面PCD B.PC BD
C.二面角P DC B的大小为 D.PC与平面 PED所成角的正切值为 2
4
第 II 卷(非选择题)
三、填空题(本题共 4小题,每题 5分,共 20 分)
13.为了了解高一、高二、高三年级学生的身体状况,现用分层随机抽样的方法抽取一
个容量为1200的样本,三个年级学生人数之比依次为 k : 5 : 3 .已知高一年级共抽取了 240
人,则高三年级抽取的人数为___________人.
14.已知空间向量a,b,c满足a b c 0 , a 3, b 1, c 4,则a b b c c a的值为
试卷第 3 页,共 5 页
________.
15.已知三棱锥P ABC内接于半径为 5 的球, ACB 90 ,AC 7 ,BC = 15 ,则
三棱锥P ABC体积的最大值为________
16.设e1 ,e2 为单位向量,满足 | 2e1 e2 | 2 ,a e1 e2 ,b 3e1 e2 ,设a,b的夹角
为 ,则cos2 的最小值为_______.
四、(解答题共 70 分,解答题应写出文字说明,证明过程或演算步骤。)
17(10 分).已知向量a 3,2 ,b x , 1 .
(1)当 2a b b时,求 a 2b ;
(2)当 c 8, 1 ,a// b c ,求向量a与b的夹角 .
sin A sin B sinC sin B
18.(12 分)已知 ABC的内角 A,B,C满足 .
sinC sin B sinC sin A
(1)求角A ;
(2)若 ABC的外接圆半径为 1,求 ABC的面积S 的最大值.
19.(12 分)进行垃圾分类收集可以减少垃圾处理量和处理设备,降低处理成本,减少土
地资源的消耗,具有社会 经济 生态等多方面的效益,是关乎生态文明建设全局的大事.
为了普及垃圾分类知识,某学校举行了垃圾分类知识考试,试卷中只有两道题目,已知
甲同学答对每题的概率都为 p,乙同学答对每题的概率都为q p q ,且在考试中每人
1
各题答题结果互不影响.已知每题甲,乙同时答对的概率为 ,恰有一人答对的概率为
2
5
.
12
(1)求 p和q的值;
(2)试求两人共答对 3 道题的概率.
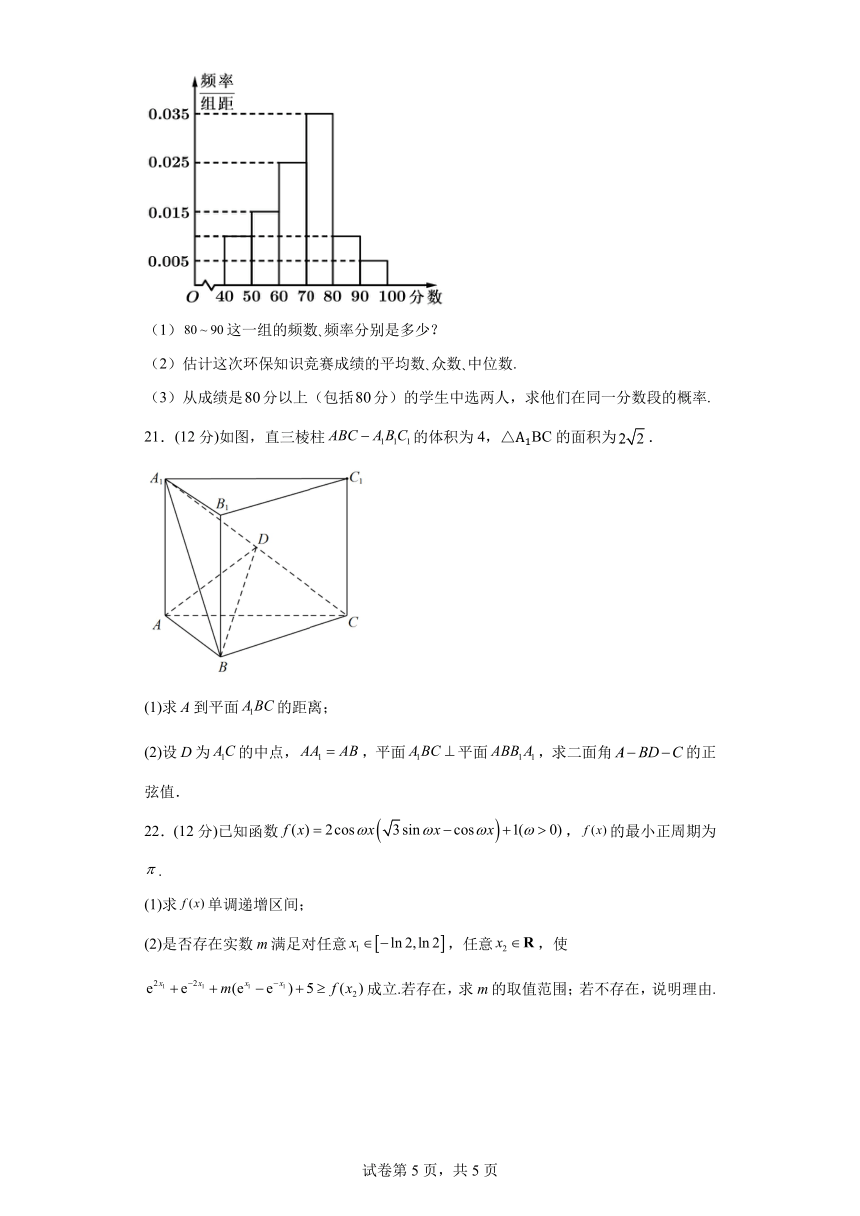
20.(12 分)如图,从参加环保知识竞赛的学生中抽出 40名,将其成绩(均.为.整.数.)整
理后画出的频率分布直方图如下:观察图形,回答下列问题:
试卷第 4 页,共 5 页
(1)80 ~ 90 这一组的频数 频率分别是多少?
(2)估计这次环保知识竞赛成绩的平均数 众数 中位数.
(3)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.
21.(12 分)如图,直三棱柱 ABC A1B1C1的体积为 4,△A BC 的面积为2 2 .
(1)求 A到平面 A1BC的距离;
(2)设 D为 A1C的中点,AA1 AB,平面 A1BC 平面 ABB1A1 ,求二面角 A BD C的正
弦值.
22.(12 分)已知函数 f (x) 2cos x 3 sin x cos x 1( 0) , f (x) 的最小正周期为
.
(1)求 f (x) 单调递增区间;
(2)是否存在实数 m满足对任意 x1 ln 2, ln 2 ,任意 x2 R,使
e2x1 e 2x1 m(ex1 e x1 ) 5 f (x2 ) 成立.若存在,求 m的取值范围;若不存在,说明理由.
试卷第 5 页,共 5 页
参考答案:
1.D
【分析】求出集合M ,N后可求M N .
1 1
【详解】M {x∣0 x 16},N {x∣x },故M N x x 16 ,
3 3
故选:D
2.B
【分析】利用复数四则运算,先求出 z,再计算复数的模.
3 4i 3 4i i
z 4 3i 2 2【详解】由题意有 ,故 | z | 4 3 5. i i i
故选:B.
3.C
4.B
【分析】求出以 P为球心,5 为半径的球与底面 ABC的截面圆的半径后可求区域的面积.
【详解】
设顶点 P在底面上的投影为O,连接BO,则O为三角形 ABC的中心,
2 3
且BO 6 2 3 ,故PO 36 12 2 6 .
3 2
因为PQ 5,故OQ 1,
故S 的轨迹为以O为圆心,1 为半径的圆,
答案第 1 页,共 15 页
3
2 36
而三角形 ABC内切圆的圆心为O,半径为 4 ,
3 1
3 6
故S 的轨迹圆在三角形 ABC内部,故其面积为
故选:B
5.C
【分析】在棱长为 2 的正方体 ABCD A1B1C1D1 中,A1B1 的中点是 P,过点 A1作与截面PBC1
平行的截面,则该截面是一个对角线分别为正方体体对角线和面对角线的菱形,进而得到答
案
【详解】在棱长为 2 的正方体 ABCD A1B1C1D1 中,A1B1 的中点是 P,过点 A1作与截面PBC1
平行的截面,则该截面是一个对角线分别为正方体体对角线和面对角线的菱形,如下图所示:
则EF 2 2 , A1C 2 3 , EF A1C
1
则截面的面积 S EF A1C 2 6 2
故选C
【点睛】本题主要考查的知识点是空间立体几何中截面的形状的判断,面面平行性质,四棱
柱的结构特征,解答本题的关键是画出截面,并分析其几何特征,属于中档题.
6.D
【分析】依题意建立平面直角坐标系,设P cosθ, sinθ ,表示出PA,PB,根据数量积的
坐标表示、辅助角公式及正弦函数的性质计算可得;
【详解】解:依题意如图建立平面直角坐标系,则C 0,0 , A 3,0 ,B 0,4 ,
答案第 2 页,共 15 页
因为PC 1,所以 P在以C为圆心,1为半径的圆上运动,
设P cosθ, sinθ , 0,2 ,
所以PA 3 cos , sin ,PB cos , 4 sin ,
所以PA PB cos 3 cos 4 sin sin
cos2 3cos 4sin sin2
1 3cos 4sin
41 5sin ,其中 sin 3 , cos ,
5 5
因为 1 sin 1,所以 4 1 5sin 6,即PA PB 4,6 ;
故选:D
7.B
【详解】设A 与 B中至少有一个不闭合的事件为T ,E与 F 至少有一个不闭合的事件为 R,则
1 1 3P T P R 1 ,所以灯亮的概率为P 1 P T P R
2 2 4
3 3 1 1 55P C P D 1 , 故选 B.
4 4 2 2 64
【方法点睛】本题主要考查独立事件、对立事件的概率公式,属于难题.解答这类综合性的
概率问题一定要把事件的独立性、互斥性与对立性结合起来,要会对一个复杂的随机事件进
答案第 3 页,共 15 页
行分析,也就是说能把一个复杂的事件分成若干个互斥事件的和,再把其中的每个事件拆成
若干个相互独立的事件的积,这种把复杂事件转化为简单事件,综合事件转化为单一事件的
思想方法在概率计算中特别重要.
8.D
【分析】通过 f x 1 是奇函数和 f x 2 是偶函数条件,可以确定出函数解析式
f x 2x2 2 ,进而利用定义或周期性结论,即可得到答案.
【详解】因为 f x 1 是奇函数,所以 f x 1 f x 1 ①;
因为 f x 2 是偶函数,所以 f x 2 f x 2 ②.
令 x 1,由①得: f 0 f 2 4a b ,由②得: f 3 f 1 a b,
因为 f 0 f 3 6,所以 4a b a b 6 a 2,
令 x 0,由①得: f 1 f 1 f 1 0 b 2,所以 f x 2x2 2 .
思路一:从定义入手.
9 5 5 1
f f 2 f 2 f
2
2 2 2
1 3 3 5
f f 1 f 1 f
2 2
2 2
5 1 1 3 f f 2
f 2 = f
2 2 2 2
9 3 5
所以 f f .
2 2 2
思路二:从周期性入手
由两个对称性可知,函数 f x 的周期T 4.
9 1 3 5
所以 f f f2
.
2 2 2
故选:D.
【点睛】在解决函数性质类问题的时候,我们通常可以借助一些二级结论,求出其周期性进
而达到简便计算的效果.
9.BD
【分析】A 选项在B A前提下,计算出P A B 0.5,P AB 0.2,即可判断;B 选项
在A 与 B互斥前提下,计算出P A B 0.7,P AB 0,即可判断;C、D 选项在A 与B
答案第 4 页,共 15 页
相互独立前提下,计算出P A B 0.7, P AB 0.1, P AB P A P B 0.4,
P AB P A P B 0.4,即可判断.
【详解】解:A 选项:如果 B A,那么P A B 0.5,P AB 0.2,故 A 选项错误;
B 选项:如果A 与 B互斥,那么P A B 0.7,P AB 0,故 B 选项正确;
C 选项:如果A 与 B相互独立,那么P A B 0.7,P AB 0.1,故 C 选项错误;
D 选项:如果A 与 B相互独立,那么P AB P A P B 0.4,P AB P A P B 0.4,
故 D 选项正确.
故选:BD.
【点睛】本题考查在包含关系,互斥关系,相互独立的前提下的和事件与积事件的概率,是
基础题.
10.AD
【分析】根据题意可设b c 4k,c a 5k,a b 6k,进而有a 3.5k,b 2.5k,c 1.5k,
利用正弦定理、平面向量的数量积和余弦定理、三角形面积公式化简计算依次判断选项即可.
【详解】依题意,设b c 4k,c a 5k,a b 6k,所以a 3.5k,b 2.5k,c 1.5k,
A:由正弦定理得:sin A : sinB : sinC a :b : c 7 :5 :3,故选项 A 正确;
b2 c2 a2 b2 c2 a2 2.52 1.52 3.52 15
B: AB AC bccos A bc k 2 k 2 0 ,
2bc 2 2 8
15
所以CA AB AC AB k 2 0,故选项 B 错误;
8
102 62 142 1
C:若 c 6 ,则k 4,所以a 14,b 10,所以cos A ,
2 10 6 2
3 1 1 3
所以sin A ,故 ABC的面积是: bc sin A 6 10 15 3,
2 2 2 2
故选项 C 错误;
5
2 32 72 1
D:若b c 8,则k 2,所以a 7,b 5,c 3,所以cos A ,
2 5 3 2
3 1 a 7 3
所以sin A ,则利用正弦定理得: ABC的外接圆半径是: ,
2 2 sin A 3
故选项 D 正确.
故选:AD
11.ABC
答案第 5 页,共 15 页
【分析】根据函数 f x Asin x 的部分图象求出函数解析式,然后根据正弦函数的性
质一一判断.
1 2
【详解】解:由函数的图象可得 A 2,由 ,求得 2.
4 3 12
再根据五点法作图可得2 2k ,又 ,求得 ,
3 2 3
∴ 函数 f x 2sin 2x ,
3
2 5
当 x 时, f x 2sin
3 3
2sin 3 ,不是最值,故 A 不成立;
3
5
当 x 时, f x 2sin 2,不等于零,故 B 不成立;
12 2
将函数 y 3 sin 2x cos 2x 2sin 2x 的图象向左平移 个单位得到函数
6 2
5
y sin 2
x
sin
2x
的图象,故 C 不成立;
2 6
6
2
当 x
,0 时,2x , , 2 3 3 3
∵
2
3
sin sin 3 3
,sin 1,
2 2
故方程 f x m在 ,0 上有两个不相等的实数根时,则m的取值范围是 2, 3 ,故 2
D 成立.
故选:ABC.
【点睛】本题考查三角函数的图象与性质,解答的关键是由函数 f x Asin x 的部分
图象求出函数解析式,属于基础题.
12.ABC
【解析】先证明 PE 平面DEBC,得 PE DC,再结合DC DE,即证DC 平面 PED,
所以平面PED 平面PCD,判断A正确;利用投影判断PC BD,判断B正确;先判断 PDE
即为二面角P DC B的平面角,再等腰直角三角形判断 PDE ,即 C 正确;先判断
4
CD
CPD为PC与平面 PED所成的角,再求正切 tan CPD ,即知 D 错误.
PD
【详解】由题易知EC 2 2 ,又PE 2, PC 2 3 ,
所以 PE2 EC2 PC2 ,所以PE EC,
答案第 6 页,共 15 页
又 PE ED,ED EC E,所以PE 平面DEBC,
所以PE DC,又DC DE,PE DE E,
所以DC 平面 PED,
又DC 平面PCD,所以平面PED 平面PCD,故 A 正确;
PC在平面EBCD内的射影为 EC,
又 EBCD为正方形,所以BD EC, PC BD,故 B 正确;
易知 PDE 即为二面角P DC B的平面角,
又 PE ED,PE ED,所以 PDE ,故 C 正确;
4
易知 CPD为PC与平面 PED所成的角,
又PD 2 2 ,CD 2,CD PD,
CD 2 2
所以 tan CPD ,故 D 错误.
PD 2 2 2
【点睛】求空间中直线与平面所成角的常见方法为:
(1)定义法:直接作平面的垂线,找到线面成角;
(2)等体积法:不作垂线,通过等体积法间接求点到面的距离,距离与斜线长的比值即线
面成角的正弦值;
(3)向量法:利用平面法向量与斜线方向向量所成的余弦值的绝对值,即是线面成角的正
弦值.本题使用了定义法.
13.360
【分析】根据高一年级学生所占的比例,求出 k,得到高三年级抽取的人数.
240 1 k 1
【详解】由已知高一年级抽取的比例为 ,所以 ,得k 2,
1200 5 k 5 3 5
3
故高三年级抽取的人数为1200 360 .
2 5 3
故答案为:360
14.-13
【分析】结合空间向量的数量积的定义以及运算律即可求出结果.
2 2 2 2
【详解】因为a b c 0 ,所以 a b c 0,则a b c 2 a b b c c a 0
32 12 42
因此a b b c c a 13
2
故答案为: 13
答案第 7 页,共 15 页
15 28 15.
3
【分析】要使三棱锥P ABC的体积最大,则平面PAB 平面 ABC,且 P在底面 ABC上的
射影为 AB中点O,利用已知条件求出三棱锥的高,再由棱锥体积公式求解即可.
【详解】解:如图,在三角形 ABC中,由 ACB 90 , AC 7 , BC = 15 ,
得 AB 49 15 8,
要使三棱锥P ABC的体积最大,则平面 PAB 平面 ABC,且 P在底面 ABC上的射影为 AB
中点O,
连接PO并延长,交三棱锥P ABC的外接球于D,则PD为球的直径,
设PO h,则 h(10 h) 4 4 16,解得h 2(舍 )或 h 8.
1 1 28 15三棱锥的体积的最大值为 7 15 8 .
3 2 3
28 15
故答案为: .
3
【点睛】本题考查三棱锥的体积的求法,考查空间想象能力与运算求解能力,属于中档题.
28
16.
29
ur ur 3
【分析】利用向量模的平方等于向量的平方化简条件得 e1 e2 ,再根据向量夹角公式求4
cos2 函数关系式,根据函数单调性求最值.
ur ur
【详解】Q| 2e1 e2 | 2 ,
ur ur
4 4e1 e2 1 2,
ur ur 3
e1 e2 , 4
r r ur ur ur ur
(a b)2 (4 4e e )2 4(1 e e )
cos2 r 2 r 2 ur ur
1 2 ur ur ur1 ur2
a b (2 2e1 e2 )(10 6e1 e2 ) 5 3e1 e2
答案第 8 页,共 15 页
4 2 4 2 28
(1 ur ur ) (1 )
3 5 3e1 e 3 32 5 29 . 3
4
28
故答案为: .
29
【点睛】本题考查利用模求向量数量积、利用向量数量积求向量夹角、利用函数单调性求最
值,考查综合分析求解能力,属中档题.
17.(1)5或13
(2)
4
【解析】(1)向量a 3,2 ,b x , 1 ,则2a b 6 x,5 ,a 2b 3 2x,0 .由 2a b b ,
可得 2a b b 0即 6 x,5 x, 1 0,即 x2 6x 5 0,解得 x 1或 x 5 ,当 x 1 ,则,则
a 2b 5,0 ,所以 a 2b 5,当 x 5,a 2b 13,0 , a 2b 13 ,综上
a 2b 5或13 .
(2)由 c ( 8, 1),b (x, 1) , a (3,2) ,则b c (x 8, 2)由 a / /(b c) ,可得
3 ( 2) 2 (x 8) 0 ,解得 x 5 ,所以 | a | 13,| b | 26 , a b 3 5 2 ( 1) 13 ,
a b 13 2cos 又 0,
,所以 .
| a | |b | 13 26 2 4
2
18.(1) A . (2) 3
3 4
【分析】(1)先设内角 A,B,C所对的边分别为a,b,c,由题意中条件,根据正弦定理得到
b2 c2 a2 bc,再由余弦定理,即可求出角A ;
(2)先由 ABC的外接圆半径为 1,结合正弦定理得到a 2sin A 3 ,再由余弦定理,结
合基本不等式,可得bc 1,从而可得三角形面积的最大值.
【详解】(1)设内角 A,B,C所对的边分别为a,b,c,
sin A sin B sinC sin B a b c b
由 可得 b2 c2 a2 bc,
sinC sin B sinC sin A c b c a
b2 c2 a2 bc 1
所以cos A ,
2bc 2bc 2
2
又因为0 A ,所以 A .
3
答案第 9 页,共 15 页
(2)因为 ABC的外接圆半径为 1,
a 2
所以有 = 2R = 2,即a 2sin A 2sin 3 ,
sin A 3
由余弦定理可得a2 b2 c2 2bccos A
即3 b 2 c 2 bc 2bc bc 3bc ,
1 1 3 3即bc 1,所以 S bc sin A 1 (当且仅当b c时取等号).
2 2 2 4
【点睛】本题主要考查解三角形,熟记正弦定理与余弦定理,以及基本不等式即可,属于常
考题型.
3 2 5
19.(1) p ,q ;(2) .
4 3 12
【解析】(1)由互斥事件和对立事件的概率公式列方程组可解得 p,q;
(2)分别求出两人答对 1 道的概率,答对两道题的概率,两人共答对 3 道题,则是一人答
对 2 道题另一人答对 1 道题,由互斥事件和独立事件概率公式可得结论.
【详解】解:(1)设 A {甲同学答对第一题},B {乙同学答对第一题},则P A p,
P B q .
设C {甲、乙二人均答对第一题},D = {甲、乙二人中恰有一人答对第一题},
则C AB,D AB AB .
由于二人答题互不影响,且每人各题答题结果互不影响,所以A 与 B相互独立,AB与 AB相
互互斥,所以P C P AB P A P B ,P D P AB AB
P AB P AB P A P B P A P B P A 1 P B 1 P A P B .
1
pq , 2
由题意可得
5p 1 q q 1 p ,
12
1 3 2
pq , p , p , 2 4 3
即 解得 或
17 2 3p q . q , q .
12 3 4
由于 p q
3 2
,所以 p ,q .
4 3
(2)设 Ai {甲同学答对了 i道题},Bi {乙同学答对了 i道题}, i 0,1,2.
1 3 3 1 3由题意得,P A1 ,P A
3 3 9
,
4 4 4 4 8 2 4 4 16
答案第 10 页,共 15 页
2 1 1 2 4 2 2 4P B1 ,P B . 3 3 3 3 9 2 3 3 9
设 E {甲乙二人共答对 3 道题},则E A1B2 A2B1 .
由于 Ai和Bi相互独立, A1B2 与 A2B1相互互斥,
所以P E P A1B2
3 4 9 4 5
P A2B1 P A1 P B2 P A2 P B1 . 8 9 16 9 12
5
所以,甲乙二人共答对 3 道题的概率为 .
12
【点睛】关键点点睛:本题考查互斥事件与独立事件的概率公式,解题关键是把所求概率事
件用互斥事件表示,然后求概率,如设 A {甲同学答对第一题},B {乙同学答对第一题},
设C {甲、乙二人均答对第一题},D = {甲、乙二人中恰有一人答对第一题},则C AB,
D AB AB.同样两人共答对 3 题分拆成甲答对 2 题乙答对 1 题与甲答对 1 题乙答对 2 题
两个互斥事件.
7
20.(1)4,0.1;(2)68.5,75,70 ;(3) .
15
【分析】(1)根据频率分步直方图的意义,计算可得 40~50、50~60、60~70、70~80、
90~100 这 5 组的频率,由频率的性质可得 80~90 这一组的频率,进而由频率、频数的关
系,计算可得答案;
(2)根据频率分步直方图中计算平均数、众数、中位数的方法,计算可得答案;
(3)记“取出的 2 人在同一分数段”为事件 E,计算可得 80~90 之间与 90~100 之间的人数,
并设为 a、b、c、d,和 A、B,列举可得从中取出 2 人的情况,可得其情况数目与取出的 2
人在同一分数段的情况数目,由等可能事件的概率公式,计算可得答案.
【详解】(1)根据题意,40 ~ 50的这一组的频率为0.01 10 0.1,
50 ~ 60的这一组的频率为0.015 10 0.15,
60 ~ 70 的这一组的频率为0.025 10 0.25,
70 ~ 80的这一组的频率为0.035 10 0.35,
90 ~ 100的这一组的频率为0.005 10 0.05,
则80 ~ 90 这一组的频率为1 0.1 0.15 0.25 0.35 0.05 0.1,
其频数为 40 0.1 4;
(2)这次竞赛的平均数为 45 0.1 55 0.15 65 0.25 75 0.35 85 0.1 95 0.05 68.5,
70 ~ 80一组的频率最大,人数最多,则众数为75,
答案第 11 页,共 15 页
70 分左右两侧的频率均为0.5,则中位数为70 ;
(3)记“取出的2 人在同一分数段”为事件E,
因为80 ~ 90 之间的人数为 40 0.1 4,设为a b c d ,
90 ~ 100之间有 40 0.05 2人,设为A B,
从这6人中选出2 人,有
a,b 、 a,c 、 a,d 、 a, A a,B 、 b,c 、 b,d 、
b, A 、 b,B 、 c,d 、 c, A c,B 、 d , A 、 d ,B 、
A,B ,共15个基本事件,
其中事件 E包括 a,b 、 a,c 、 a,d 、 b,c 、 b,d 、 c,d 、 A,B ,共 7 个基本事件,
则 P 7E .
15
21.(1) 2
(2) 3
2
【分析】(1)由等体积法运算即可得解;
(2)由面面垂直的性质及判定可得BC 平面 ABB1A1,建立空间直角坐标系,利用空间向
量法即可得解.
(1)
在直三棱柱 ABC A1B1C1中,设点 A到平面 A1BC的距离为 h,
1 2 2 1 1 4
则VA A BC S A BC h h VA ABC S A A V , 1 3 1 3 1 3 ABC 1 3 ABC A
1B1C1 3
解得h 2 ,
所以点 A到平面 A1BC的距离为 2 ;
(2)
取 A1B的中点 E,连接 AE,如图,因为 AA1 AB,所以 AE A1B ,
又平面 A1BC 平面 ABB1A1,平面 A1BC 平面 ABB1A1 A1B,
且 AE 平面 ABB1A1,所以 AE⊥平面 A1BC,
答案第 12 页,共 15 页
在直三棱柱 ABC A1B1C1中, BB1 平面 ABC,
由BC 平面 A1BC,BC 平面 ABC可得 AE BC, BB1 BC ,
又 AE,BB1 平面 ABB1A1且相交,所以BC 平面 ABB1A1 ,
所以BC,BA,BB1 两两垂直,以 B为原点,建立空间直角坐标系,如图,
由(1)得 AE 2 ,所以 AA1 AB 2, A1B 2 2 ,所以BC 2,
则 A 0, 2,0 , A1 0, 2, 2 ,B 0,0,0 ,C 2,0,0 ,所以 A1C的中点D 1,1,1 ,
则BD 1,1,1 ,BA 0,2,0 ,BC 2,0,0 ,
m BD x y z 0
设平面 ABD的一个法向量m x, y, z ,则 ,
m BA 2y 0
可取m 1,0, 1 ,
m BD a b c 0
设平面BDC的一个法向量n a,b,c ,则 ,
m BC 2a 0
r
可取n 0,1, 1 ,
m n 1 1
则 cos m,n ,
m n 2 2 2
2
1 3
所以二面角 A BD C的正弦值为 1 .
2 2
答案第 13 页,共 15 页
22.(1) k ,k , k Z 6 3
29 29
(2)存在, ,
6 6
【分析】(1)由二倍角和辅助角公式化简后,根据题意可求得解析式,然后利用正弦函数性
质可得单调增区间;
(2)将问题转化为e2x1 e 2x1 m(ex1 e x1 ) 5 f (x),然后令ex1max e x1 t ,将问题转化为
一元二次不等式恒成立问题,利用二次函数性质可解.
(1)
f x 3 sin 2 x 2cos2 x 1 3 sin 2 x cos 2 x 2sin 2 x 6
2
∵ f (x) 的最小正周期为 , 0,∴ ,∴ 1
2
∴ f (x) 的解析式为 f (x)
2sin 2x
6
由题意得:2k 2x 2k , k Z ∴ k - #x k + ,k Z
2 6 2 6 3
故函数 f (x) 2sin 2x 的单调递增区间为 k ,k , k Z. 6 6 3
(2)
由(1)可知 f (x) 2sin 2x , f (x2 )max 2
6
∴ 实数 m满足对任意 x1 ln 2, ln 2 ,
x R e2x1 e 2x1 m(ex1 e x任意 2 ,使得 1 ) 5 f (x2 ) 成立
即 e2x1 e 2x1 m(ex1 e x1 ) 5 2成立
令 y e2x1 e 2x1 m(ex1 e x1 ) 3,设ex1 e x 2x 2x1 t ,那么e 1 e 1 (ex1 e x1 )2 2 t 2 2
3 3
∵ x1 ln 2, ln 2 ,∴ t , , 2 2
3 3
可等价转化为: t2 mt 5 0 在 t
, 上恒成立
2 2
m 3 3
令 g(t) t2 mt 5,其对称轴 t ,∵ t , 上,
2 2 2
m 3 3 29 3m 29
∴ ①当 时,即m 3, g(t) g
min 0,解得3 m ; 2 2 2 4 2 6
答案第 14 页,共 15 页
3 m 3 m m2
②当 ,即 33 m 3 29 3m 29
③当
,即m 3时, g(t)min g 0,解得 m 3; 2 2 2 4 2 6
29 29
综上可得,存在 m,可知 m的取值范围是 , .
6 6
答案第 15 页,共 15 页
高二一期入学试卷
考试分值:150 分;考试时间:120 分钟;命题人:
第 I卷(选择题)
一.选择题:本大题共 8 小题,每小题 5分,共 40 分,在每个小题给出的 4个选项中,只有
一项是符合题目要求的.
1.若集合M {x∣ x 4}, N {x∣3x 1},则M N ( )
1 A. x 0 x 2 B. x x 2 C. 1 x 3 x 16 D. x x 16
3 3
2.若复数 z满足 i z 3 4i ,则 z ( )
A.1 B.5 C.7 D.25
3.已知向量a (3, 4),b (1,0),c a tb,若 a,c b,c ,则 t ( )
A. 6 B. 5 C.5 D.6
4.已知正三棱锥P ABC的六条棱长均为 6,S是 ABC及其内部的点构成的集合.设
集合T Q S PQ 5 ,则 T表示的区域的面积为( )
3
A. B. C.2 D.3
4
5.如图,在棱长为 2 的正方体 ABCD A1B1C1D1 中,A1B1 的中点是 P,过点 A1作与截面
PBC1平行的截面,则该截面的面积为( )
A.2 2 B.2 3 C.2 6 D.4
6.在 ABC中, AC 3,BC 4, C 90 .P为 ABC所在平面内的动点,且 PC 1,
则PA PB的取值范围是( )
A.[ 5,3] B.[ 3,5] C.[ 6,4] D.[ 4,6]
1
7.一个电路如图所示,A,B,C,D,E,F 为 6 个开关,其闭合的概率为 ,且是相
2
互独立的,则灯亮的概率是( )
试卷第 1 页,共 5 页
1 55 1 1
A. B. C. D.
64 64 8 16
8.设函数 f x 的定义域为 R, f x 1 为奇函数, f x 2 为偶函数,当 x 1,2 时,
9
f (x) ax2 b.若 f 0 f 3 6,则 f ( )
2
9 3 7 5
A. B. C. D.
4 2 4 2
二、多选题(4 个小题每个题 5分共计 20 分,在每个小题给出的四个选项中,有多项符
合题目要求。全部选对得 5分,部分对的得 2分,有选错的得 0分。)
9.已知事件A , B,且P A 0.5,P B 0.2,则下列结论正确的是( )
A.如果B A,那么P A B 0.2,P AB 0.5
B.如果A 与 B互斥,那么P A B 0.7,P AB 0
C.如果A 与 B相互独立,那么P A B 0.7,P AB 0
D.如果A 与 B相互独立,那么 P AB 0.4 ,P AB 0.4
10.在 ABC中,角A , B,C所对的边分别为a,b,c,已知
b c : c a : a b 4 :5 : 6 ,则下列结论正确的是( )
A.sin A : sinB : sinC 7 :5 :3
B.CA AB 0
C.若 c 6 ,则 ABC的面积是 15
D.若b c 8,则 ABC 7 3外接圆半径是
3
11.已知函数 f (x) Asin( x )
, A
0, 0, 部分图象如图所示,下列说法
2
不正确的是( )
试卷第 2 页,共 5 页
2 A. f x 的图象关于直线 x 对称
3
B. f x 5 的图象关于点 , 0 对称
12
C.将函数 y 3 sin 2x cos 2x的图象向左平移 个单位得到函数 f x 的图象
2
D.若方程 f x m 在 , 0 上有两个不相等的实数根,则 m的取值范围是 2, 3 2
1
12.如图直角梯形 ABCD中,AB//CD,AB BC,BC CD AB 2,E为 AB中点.
2
以DE 为折痕把△ADE 折起,使点 A到达点 P的位置,且PC 2 3 则( )
A.平面PED 平面PCD B.PC BD
C.二面角P DC B的大小为 D.PC与平面 PED所成角的正切值为 2
4
第 II 卷(非选择题)
三、填空题(本题共 4小题,每题 5分,共 20 分)
13.为了了解高一、高二、高三年级学生的身体状况,现用分层随机抽样的方法抽取一
个容量为1200的样本,三个年级学生人数之比依次为 k : 5 : 3 .已知高一年级共抽取了 240
人,则高三年级抽取的人数为___________人.
14.已知空间向量a,b,c满足a b c 0 , a 3, b 1, c 4,则a b b c c a的值为
试卷第 3 页,共 5 页
________.
15.已知三棱锥P ABC内接于半径为 5 的球, ACB 90 ,AC 7 ,BC = 15 ,则
三棱锥P ABC体积的最大值为________
16.设e1 ,e2 为单位向量,满足 | 2e1 e2 | 2 ,a e1 e2 ,b 3e1 e2 ,设a,b的夹角
为 ,则cos2 的最小值为_______.
四、(解答题共 70 分,解答题应写出文字说明,证明过程或演算步骤。)
17(10 分).已知向量a 3,2 ,b x , 1 .
(1)当 2a b b时,求 a 2b ;
(2)当 c 8, 1 ,a// b c ,求向量a与b的夹角 .
sin A sin B sinC sin B
18.(12 分)已知 ABC的内角 A,B,C满足 .
sinC sin B sinC sin A
(1)求角A ;
(2)若 ABC的外接圆半径为 1,求 ABC的面积S 的最大值.
19.(12 分)进行垃圾分类收集可以减少垃圾处理量和处理设备,降低处理成本,减少土
地资源的消耗,具有社会 经济 生态等多方面的效益,是关乎生态文明建设全局的大事.
为了普及垃圾分类知识,某学校举行了垃圾分类知识考试,试卷中只有两道题目,已知
甲同学答对每题的概率都为 p,乙同学答对每题的概率都为q p q ,且在考试中每人
1
各题答题结果互不影响.已知每题甲,乙同时答对的概率为 ,恰有一人答对的概率为
2
5
.
12
(1)求 p和q的值;
(2)试求两人共答对 3 道题的概率.
20.(12 分)如图,从参加环保知识竞赛的学生中抽出 40名,将其成绩(均.为.整.数.)整
理后画出的频率分布直方图如下:观察图形,回答下列问题:
试卷第 4 页,共 5 页
(1)80 ~ 90 这一组的频数 频率分别是多少?
(2)估计这次环保知识竞赛成绩的平均数 众数 中位数.
(3)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.
21.(12 分)如图,直三棱柱 ABC A1B1C1的体积为 4,△A BC 的面积为2 2 .
(1)求 A到平面 A1BC的距离;
(2)设 D为 A1C的中点,AA1 AB,平面 A1BC 平面 ABB1A1 ,求二面角 A BD C的正
弦值.
22.(12 分)已知函数 f (x) 2cos x 3 sin x cos x 1( 0) , f (x) 的最小正周期为
.
(1)求 f (x) 单调递增区间;
(2)是否存在实数 m满足对任意 x1 ln 2, ln 2 ,任意 x2 R,使
e2x1 e 2x1 m(ex1 e x1 ) 5 f (x2 ) 成立.若存在,求 m的取值范围;若不存在,说明理由.
试卷第 5 页,共 5 页
参考答案:
1.D
【分析】求出集合M ,N后可求M N .
1 1
【详解】M {x∣0 x 16},N {x∣x },故M N x x 16 ,
3 3
故选:D
2.B
【分析】利用复数四则运算,先求出 z,再计算复数的模.
3 4i 3 4i i
z 4 3i 2 2【详解】由题意有 ,故 | z | 4 3 5. i i i
故选:B.
3.C
4.B
【分析】求出以 P为球心,5 为半径的球与底面 ABC的截面圆的半径后可求区域的面积.
【详解】
设顶点 P在底面上的投影为O,连接BO,则O为三角形 ABC的中心,
2 3
且BO 6 2 3 ,故PO 36 12 2 6 .
3 2
因为PQ 5,故OQ 1,
故S 的轨迹为以O为圆心,1 为半径的圆,
答案第 1 页,共 15 页
3
2 36
而三角形 ABC内切圆的圆心为O,半径为 4 ,
3 1
3 6
故S 的轨迹圆在三角形 ABC内部,故其面积为
故选:B
5.C
【分析】在棱长为 2 的正方体 ABCD A1B1C1D1 中,A1B1 的中点是 P,过点 A1作与截面PBC1
平行的截面,则该截面是一个对角线分别为正方体体对角线和面对角线的菱形,进而得到答
案
【详解】在棱长为 2 的正方体 ABCD A1B1C1D1 中,A1B1 的中点是 P,过点 A1作与截面PBC1
平行的截面,则该截面是一个对角线分别为正方体体对角线和面对角线的菱形,如下图所示:
则EF 2 2 , A1C 2 3 , EF A1C
1
则截面的面积 S EF A1C 2 6 2
故选C
【点睛】本题主要考查的知识点是空间立体几何中截面的形状的判断,面面平行性质,四棱
柱的结构特征,解答本题的关键是画出截面,并分析其几何特征,属于中档题.
6.D
【分析】依题意建立平面直角坐标系,设P cosθ, sinθ ,表示出PA,PB,根据数量积的
坐标表示、辅助角公式及正弦函数的性质计算可得;
【详解】解:依题意如图建立平面直角坐标系,则C 0,0 , A 3,0 ,B 0,4 ,
答案第 2 页,共 15 页
因为PC 1,所以 P在以C为圆心,1为半径的圆上运动,
设P cosθ, sinθ , 0,2 ,
所以PA 3 cos , sin ,PB cos , 4 sin ,
所以PA PB cos 3 cos 4 sin sin
cos2 3cos 4sin sin2
1 3cos 4sin
41 5sin ,其中 sin 3 , cos ,
5 5
因为 1 sin 1,所以 4 1 5sin 6,即PA PB 4,6 ;
故选:D
7.B
【详解】设A 与 B中至少有一个不闭合的事件为T ,E与 F 至少有一个不闭合的事件为 R,则
1 1 3P T P R 1 ,所以灯亮的概率为P 1 P T P R
2 2 4
3 3 1 1 55P C P D 1 , 故选 B.
4 4 2 2 64
【方法点睛】本题主要考查独立事件、对立事件的概率公式,属于难题.解答这类综合性的
概率问题一定要把事件的独立性、互斥性与对立性结合起来,要会对一个复杂的随机事件进
答案第 3 页,共 15 页
行分析,也就是说能把一个复杂的事件分成若干个互斥事件的和,再把其中的每个事件拆成
若干个相互独立的事件的积,这种把复杂事件转化为简单事件,综合事件转化为单一事件的
思想方法在概率计算中特别重要.
8.D
【分析】通过 f x 1 是奇函数和 f x 2 是偶函数条件,可以确定出函数解析式
f x 2x2 2 ,进而利用定义或周期性结论,即可得到答案.
【详解】因为 f x 1 是奇函数,所以 f x 1 f x 1 ①;
因为 f x 2 是偶函数,所以 f x 2 f x 2 ②.
令 x 1,由①得: f 0 f 2 4a b ,由②得: f 3 f 1 a b,
因为 f 0 f 3 6,所以 4a b a b 6 a 2,
令 x 0,由①得: f 1 f 1 f 1 0 b 2,所以 f x 2x2 2 .
思路一:从定义入手.
9 5 5 1
f f 2 f 2 f
2
2 2 2
1 3 3 5
f f 1 f 1 f
2 2
2 2
5 1 1 3 f f 2
f 2 = f
2 2 2 2
9 3 5
所以 f f .
2 2 2
思路二:从周期性入手
由两个对称性可知,函数 f x 的周期T 4.
9 1 3 5
所以 f f f2
.
2 2 2
故选:D.
【点睛】在解决函数性质类问题的时候,我们通常可以借助一些二级结论,求出其周期性进
而达到简便计算的效果.
9.BD
【分析】A 选项在B A前提下,计算出P A B 0.5,P AB 0.2,即可判断;B 选项
在A 与 B互斥前提下,计算出P A B 0.7,P AB 0,即可判断;C、D 选项在A 与B
答案第 4 页,共 15 页
相互独立前提下,计算出P A B 0.7, P AB 0.1, P AB P A P B 0.4,
P AB P A P B 0.4,即可判断.
【详解】解:A 选项:如果 B A,那么P A B 0.5,P AB 0.2,故 A 选项错误;
B 选项:如果A 与 B互斥,那么P A B 0.7,P AB 0,故 B 选项正确;
C 选项:如果A 与 B相互独立,那么P A B 0.7,P AB 0.1,故 C 选项错误;
D 选项:如果A 与 B相互独立,那么P AB P A P B 0.4,P AB P A P B 0.4,
故 D 选项正确.
故选:BD.
【点睛】本题考查在包含关系,互斥关系,相互独立的前提下的和事件与积事件的概率,是
基础题.
10.AD
【分析】根据题意可设b c 4k,c a 5k,a b 6k,进而有a 3.5k,b 2.5k,c 1.5k,
利用正弦定理、平面向量的数量积和余弦定理、三角形面积公式化简计算依次判断选项即可.
【详解】依题意,设b c 4k,c a 5k,a b 6k,所以a 3.5k,b 2.5k,c 1.5k,
A:由正弦定理得:sin A : sinB : sinC a :b : c 7 :5 :3,故选项 A 正确;
b2 c2 a2 b2 c2 a2 2.52 1.52 3.52 15
B: AB AC bccos A bc k 2 k 2 0 ,
2bc 2 2 8
15
所以CA AB AC AB k 2 0,故选项 B 错误;
8
102 62 142 1
C:若 c 6 ,则k 4,所以a 14,b 10,所以cos A ,
2 10 6 2
3 1 1 3
所以sin A ,故 ABC的面积是: bc sin A 6 10 15 3,
2 2 2 2
故选项 C 错误;
5
2 32 72 1
D:若b c 8,则k 2,所以a 7,b 5,c 3,所以cos A ,
2 5 3 2
3 1 a 7 3
所以sin A ,则利用正弦定理得: ABC的外接圆半径是: ,
2 2 sin A 3
故选项 D 正确.
故选:AD
11.ABC
答案第 5 页,共 15 页
【分析】根据函数 f x Asin x 的部分图象求出函数解析式,然后根据正弦函数的性
质一一判断.
1 2
【详解】解:由函数的图象可得 A 2,由 ,求得 2.
4 3 12
再根据五点法作图可得2 2k ,又 ,求得 ,
3 2 3
∴ 函数 f x 2sin 2x ,
3
2 5
当 x 时, f x 2sin
3 3
2sin 3 ,不是最值,故 A 不成立;
3
5
当 x 时, f x 2sin 2,不等于零,故 B 不成立;
12 2
将函数 y 3 sin 2x cos 2x 2sin 2x 的图象向左平移 个单位得到函数
6 2
5
y sin 2
x
sin
2x
的图象,故 C 不成立;
2 6
6
2
当 x
,0 时,2x , , 2 3 3 3
∵
2
3
sin sin 3 3
,sin 1,
2 2
故方程 f x m在 ,0 上有两个不相等的实数根时,则m的取值范围是 2, 3 ,故 2
D 成立.
故选:ABC.
【点睛】本题考查三角函数的图象与性质,解答的关键是由函数 f x Asin x 的部分
图象求出函数解析式,属于基础题.
12.ABC
【解析】先证明 PE 平面DEBC,得 PE DC,再结合DC DE,即证DC 平面 PED,
所以平面PED 平面PCD,判断A正确;利用投影判断PC BD,判断B正确;先判断 PDE
即为二面角P DC B的平面角,再等腰直角三角形判断 PDE ,即 C 正确;先判断
4
CD
CPD为PC与平面 PED所成的角,再求正切 tan CPD ,即知 D 错误.
PD
【详解】由题易知EC 2 2 ,又PE 2, PC 2 3 ,
所以 PE2 EC2 PC2 ,所以PE EC,
答案第 6 页,共 15 页
又 PE ED,ED EC E,所以PE 平面DEBC,
所以PE DC,又DC DE,PE DE E,
所以DC 平面 PED,
又DC 平面PCD,所以平面PED 平面PCD,故 A 正确;
PC在平面EBCD内的射影为 EC,
又 EBCD为正方形,所以BD EC, PC BD,故 B 正确;
易知 PDE 即为二面角P DC B的平面角,
又 PE ED,PE ED,所以 PDE ,故 C 正确;
4
易知 CPD为PC与平面 PED所成的角,
又PD 2 2 ,CD 2,CD PD,
CD 2 2
所以 tan CPD ,故 D 错误.
PD 2 2 2
【点睛】求空间中直线与平面所成角的常见方法为:
(1)定义法:直接作平面的垂线,找到线面成角;
(2)等体积法:不作垂线,通过等体积法间接求点到面的距离,距离与斜线长的比值即线
面成角的正弦值;
(3)向量法:利用平面法向量与斜线方向向量所成的余弦值的绝对值,即是线面成角的正
弦值.本题使用了定义法.
13.360
【分析】根据高一年级学生所占的比例,求出 k,得到高三年级抽取的人数.
240 1 k 1
【详解】由已知高一年级抽取的比例为 ,所以 ,得k 2,
1200 5 k 5 3 5
3
故高三年级抽取的人数为1200 360 .
2 5 3
故答案为:360
14.-13
【分析】结合空间向量的数量积的定义以及运算律即可求出结果.
2 2 2 2
【详解】因为a b c 0 ,所以 a b c 0,则a b c 2 a b b c c a 0
32 12 42
因此a b b c c a 13
2
故答案为: 13
答案第 7 页,共 15 页
15 28 15.
3
【分析】要使三棱锥P ABC的体积最大,则平面PAB 平面 ABC,且 P在底面 ABC上的
射影为 AB中点O,利用已知条件求出三棱锥的高,再由棱锥体积公式求解即可.
【详解】解:如图,在三角形 ABC中,由 ACB 90 , AC 7 , BC = 15 ,
得 AB 49 15 8,
要使三棱锥P ABC的体积最大,则平面 PAB 平面 ABC,且 P在底面 ABC上的射影为 AB
中点O,
连接PO并延长,交三棱锥P ABC的外接球于D,则PD为球的直径,
设PO h,则 h(10 h) 4 4 16,解得h 2(舍 )或 h 8.
1 1 28 15三棱锥的体积的最大值为 7 15 8 .
3 2 3
28 15
故答案为: .
3
【点睛】本题考查三棱锥的体积的求法,考查空间想象能力与运算求解能力,属于中档题.
28
16.
29
ur ur 3
【分析】利用向量模的平方等于向量的平方化简条件得 e1 e2 ,再根据向量夹角公式求4
cos2 函数关系式,根据函数单调性求最值.
ur ur
【详解】Q| 2e1 e2 | 2 ,
ur ur
4 4e1 e2 1 2,
ur ur 3
e1 e2 , 4
r r ur ur ur ur
(a b)2 (4 4e e )2 4(1 e e )
cos2 r 2 r 2 ur ur
1 2 ur ur ur1 ur2
a b (2 2e1 e2 )(10 6e1 e2 ) 5 3e1 e2
答案第 8 页,共 15 页
4 2 4 2 28
(1 ur ur ) (1 )
3 5 3e1 e 3 32 5 29 . 3
4
28
故答案为: .
29
【点睛】本题考查利用模求向量数量积、利用向量数量积求向量夹角、利用函数单调性求最
值,考查综合分析求解能力,属中档题.
17.(1)5或13
(2)
4
【解析】(1)向量a 3,2 ,b x , 1 ,则2a b 6 x,5 ,a 2b 3 2x,0 .由 2a b b ,
可得 2a b b 0即 6 x,5 x, 1 0,即 x2 6x 5 0,解得 x 1或 x 5 ,当 x 1 ,则,则
a 2b 5,0 ,所以 a 2b 5,当 x 5,a 2b 13,0 , a 2b 13 ,综上
a 2b 5或13 .
(2)由 c ( 8, 1),b (x, 1) , a (3,2) ,则b c (x 8, 2)由 a / /(b c) ,可得
3 ( 2) 2 (x 8) 0 ,解得 x 5 ,所以 | a | 13,| b | 26 , a b 3 5 2 ( 1) 13 ,
a b 13 2cos 又 0,
,所以 .
| a | |b | 13 26 2 4
2
18.(1) A . (2) 3
3 4
【分析】(1)先设内角 A,B,C所对的边分别为a,b,c,由题意中条件,根据正弦定理得到
b2 c2 a2 bc,再由余弦定理,即可求出角A ;
(2)先由 ABC的外接圆半径为 1,结合正弦定理得到a 2sin A 3 ,再由余弦定理,结
合基本不等式,可得bc 1,从而可得三角形面积的最大值.
【详解】(1)设内角 A,B,C所对的边分别为a,b,c,
sin A sin B sinC sin B a b c b
由 可得 b2 c2 a2 bc,
sinC sin B sinC sin A c b c a
b2 c2 a2 bc 1
所以cos A ,
2bc 2bc 2
2
又因为0 A ,所以 A .
3
答案第 9 页,共 15 页
(2)因为 ABC的外接圆半径为 1,
a 2
所以有 = 2R = 2,即a 2sin A 2sin 3 ,
sin A 3
由余弦定理可得a2 b2 c2 2bccos A
即3 b 2 c 2 bc 2bc bc 3bc ,
1 1 3 3即bc 1,所以 S bc sin A 1 (当且仅当b c时取等号).
2 2 2 4
【点睛】本题主要考查解三角形,熟记正弦定理与余弦定理,以及基本不等式即可,属于常
考题型.
3 2 5
19.(1) p ,q ;(2) .
4 3 12
【解析】(1)由互斥事件和对立事件的概率公式列方程组可解得 p,q;
(2)分别求出两人答对 1 道的概率,答对两道题的概率,两人共答对 3 道题,则是一人答
对 2 道题另一人答对 1 道题,由互斥事件和独立事件概率公式可得结论.
【详解】解:(1)设 A {甲同学答对第一题},B {乙同学答对第一题},则P A p,
P B q .
设C {甲、乙二人均答对第一题},D = {甲、乙二人中恰有一人答对第一题},
则C AB,D AB AB .
由于二人答题互不影响,且每人各题答题结果互不影响,所以A 与 B相互独立,AB与 AB相
互互斥,所以P C P AB P A P B ,P D P AB AB
P AB P AB P A P B P A P B P A 1 P B 1 P A P B .
1
pq , 2
由题意可得
5p 1 q q 1 p ,
12
1 3 2
pq , p , p , 2 4 3
即 解得 或
17 2 3p q . q , q .
12 3 4
由于 p q
3 2
,所以 p ,q .
4 3
(2)设 Ai {甲同学答对了 i道题},Bi {乙同学答对了 i道题}, i 0,1,2.
1 3 3 1 3由题意得,P A1 ,P A
3 3 9
,
4 4 4 4 8 2 4 4 16
答案第 10 页,共 15 页
2 1 1 2 4 2 2 4P B1 ,P B . 3 3 3 3 9 2 3 3 9
设 E {甲乙二人共答对 3 道题},则E A1B2 A2B1 .
由于 Ai和Bi相互独立, A1B2 与 A2B1相互互斥,
所以P E P A1B2
3 4 9 4 5
P A2B1 P A1 P B2 P A2 P B1 . 8 9 16 9 12
5
所以,甲乙二人共答对 3 道题的概率为 .
12
【点睛】关键点点睛:本题考查互斥事件与独立事件的概率公式,解题关键是把所求概率事
件用互斥事件表示,然后求概率,如设 A {甲同学答对第一题},B {乙同学答对第一题},
设C {甲、乙二人均答对第一题},D = {甲、乙二人中恰有一人答对第一题},则C AB,
D AB AB.同样两人共答对 3 题分拆成甲答对 2 题乙答对 1 题与甲答对 1 题乙答对 2 题
两个互斥事件.
7
20.(1)4,0.1;(2)68.5,75,70 ;(3) .
15
【分析】(1)根据频率分步直方图的意义,计算可得 40~50、50~60、60~70、70~80、
90~100 这 5 组的频率,由频率的性质可得 80~90 这一组的频率,进而由频率、频数的关
系,计算可得答案;
(2)根据频率分步直方图中计算平均数、众数、中位数的方法,计算可得答案;
(3)记“取出的 2 人在同一分数段”为事件 E,计算可得 80~90 之间与 90~100 之间的人数,
并设为 a、b、c、d,和 A、B,列举可得从中取出 2 人的情况,可得其情况数目与取出的 2
人在同一分数段的情况数目,由等可能事件的概率公式,计算可得答案.
【详解】(1)根据题意,40 ~ 50的这一组的频率为0.01 10 0.1,
50 ~ 60的这一组的频率为0.015 10 0.15,
60 ~ 70 的这一组的频率为0.025 10 0.25,
70 ~ 80的这一组的频率为0.035 10 0.35,
90 ~ 100的这一组的频率为0.005 10 0.05,
则80 ~ 90 这一组的频率为1 0.1 0.15 0.25 0.35 0.05 0.1,
其频数为 40 0.1 4;
(2)这次竞赛的平均数为 45 0.1 55 0.15 65 0.25 75 0.35 85 0.1 95 0.05 68.5,
70 ~ 80一组的频率最大,人数最多,则众数为75,
答案第 11 页,共 15 页
70 分左右两侧的频率均为0.5,则中位数为70 ;
(3)记“取出的2 人在同一分数段”为事件E,
因为80 ~ 90 之间的人数为 40 0.1 4,设为a b c d ,
90 ~ 100之间有 40 0.05 2人,设为A B,
从这6人中选出2 人,有
a,b 、 a,c 、 a,d 、 a, A a,B 、 b,c 、 b,d 、
b, A 、 b,B 、 c,d 、 c, A c,B 、 d , A 、 d ,B 、
A,B ,共15个基本事件,
其中事件 E包括 a,b 、 a,c 、 a,d 、 b,c 、 b,d 、 c,d 、 A,B ,共 7 个基本事件,
则 P 7E .
15
21.(1) 2
(2) 3
2
【分析】(1)由等体积法运算即可得解;
(2)由面面垂直的性质及判定可得BC 平面 ABB1A1,建立空间直角坐标系,利用空间向
量法即可得解.
(1)
在直三棱柱 ABC A1B1C1中,设点 A到平面 A1BC的距离为 h,
1 2 2 1 1 4
则VA A BC S A BC h h VA ABC S A A V , 1 3 1 3 1 3 ABC 1 3 ABC A
1B1C1 3
解得h 2 ,
所以点 A到平面 A1BC的距离为 2 ;
(2)
取 A1B的中点 E,连接 AE,如图,因为 AA1 AB,所以 AE A1B ,
又平面 A1BC 平面 ABB1A1,平面 A1BC 平面 ABB1A1 A1B,
且 AE 平面 ABB1A1,所以 AE⊥平面 A1BC,
答案第 12 页,共 15 页
在直三棱柱 ABC A1B1C1中, BB1 平面 ABC,
由BC 平面 A1BC,BC 平面 ABC可得 AE BC, BB1 BC ,
又 AE,BB1 平面 ABB1A1且相交,所以BC 平面 ABB1A1 ,
所以BC,BA,BB1 两两垂直,以 B为原点,建立空间直角坐标系,如图,
由(1)得 AE 2 ,所以 AA1 AB 2, A1B 2 2 ,所以BC 2,
则 A 0, 2,0 , A1 0, 2, 2 ,B 0,0,0 ,C 2,0,0 ,所以 A1C的中点D 1,1,1 ,
则BD 1,1,1 ,BA 0,2,0 ,BC 2,0,0 ,
m BD x y z 0
设平面 ABD的一个法向量m x, y, z ,则 ,
m BA 2y 0
可取m 1,0, 1 ,
m BD a b c 0
设平面BDC的一个法向量n a,b,c ,则 ,
m BC 2a 0
r
可取n 0,1, 1 ,
m n 1 1
则 cos m,n ,
m n 2 2 2
2
1 3
所以二面角 A BD C的正弦值为 1 .
2 2
答案第 13 页,共 15 页
22.(1) k ,k , k Z 6 3
29 29
(2)存在, ,
6 6
【分析】(1)由二倍角和辅助角公式化简后,根据题意可求得解析式,然后利用正弦函数性
质可得单调增区间;
(2)将问题转化为e2x1 e 2x1 m(ex1 e x1 ) 5 f (x),然后令ex1max e x1 t ,将问题转化为
一元二次不等式恒成立问题,利用二次函数性质可解.
(1)
f x 3 sin 2 x 2cos2 x 1 3 sin 2 x cos 2 x 2sin 2 x 6
2
∵ f (x) 的最小正周期为 , 0,∴ ,∴ 1
2
∴ f (x) 的解析式为 f (x)
2sin 2x
6
由题意得:2k 2x 2k , k Z ∴ k - #x k + ,k Z
2 6 2 6 3
故函数 f (x) 2sin 2x 的单调递增区间为 k ,k , k Z. 6 6 3
(2)
由(1)可知 f (x) 2sin 2x , f (x2 )max 2
6
∴ 实数 m满足对任意 x1 ln 2, ln 2 ,
x R e2x1 e 2x1 m(ex1 e x任意 2 ,使得 1 ) 5 f (x2 ) 成立
即 e2x1 e 2x1 m(ex1 e x1 ) 5 2成立
令 y e2x1 e 2x1 m(ex1 e x1 ) 3,设ex1 e x 2x 2x1 t ,那么e 1 e 1 (ex1 e x1 )2 2 t 2 2
3 3
∵ x1 ln 2, ln 2 ,∴ t , , 2 2
3 3
可等价转化为: t2 mt 5 0 在 t
, 上恒成立
2 2
m 3 3
令 g(t) t2 mt 5,其对称轴 t ,∵ t , 上,
2 2 2
m 3 3 29 3m 29
∴ ①当 时,即m 3, g(t) g
min 0,解得3 m ; 2 2 2 4 2 6
答案第 14 页,共 15 页
3 m 3 m m2
②当 ,即 3
③当
,即m 3时, g(t)min g 0,解得 m 3; 2 2 2 4 2 6
29 29
综上可得,存在 m,可知 m的取值范围是 , .
6 6
答案第 15 页,共 15 页
同课章节目录
