2022-2023学年九年级人教版数学上册22.3.2 销售、投球、喷水问题 课时练习(含解析)
文档属性
| 名称 | 2022-2023学年九年级人教版数学上册22.3.2 销售、投球、喷水问题 课时练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 00:00:00 | ||
图片预览



文档简介
22.3.2 销售、投球、喷水问题(附解析)
一、单选题(共10个小题)
1.某商品现在的售价为每件35元,每天可卖出50件.市场调查反映:如果调整价格,每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,求最大销售额是( )
A.2500元 B.2000元 C.1800元 D.2200元
2.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
3.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是y=-2x2+60x+800,则利润获得最多为( )
A.15元 B.400元 C.800元 D.1250元
4.向上发射一枚炮弹,经秒后的高度为公尺,且时间秒与高度公尺的关系为、为常数,且若此炮弹在第秒与第秒时的高度相等,则下列哪一个时间的高度是最高的?( )
A.第秒 B.第秒 C.第秒 D.第秒
5.从地面竖直向上抛出一小球,小球的高度h(米)与运动时间t(秒)之间的关系式是h=30t﹣5t2(0≤t≤6),则小球最高时,运动的时间是( )
A.1秒 B.2秒 C.3秒 D.4秒
6.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=﹣(x﹣2)2+6,则水柱的最大高度是( )
A.2 B.4 C.6 D.2+
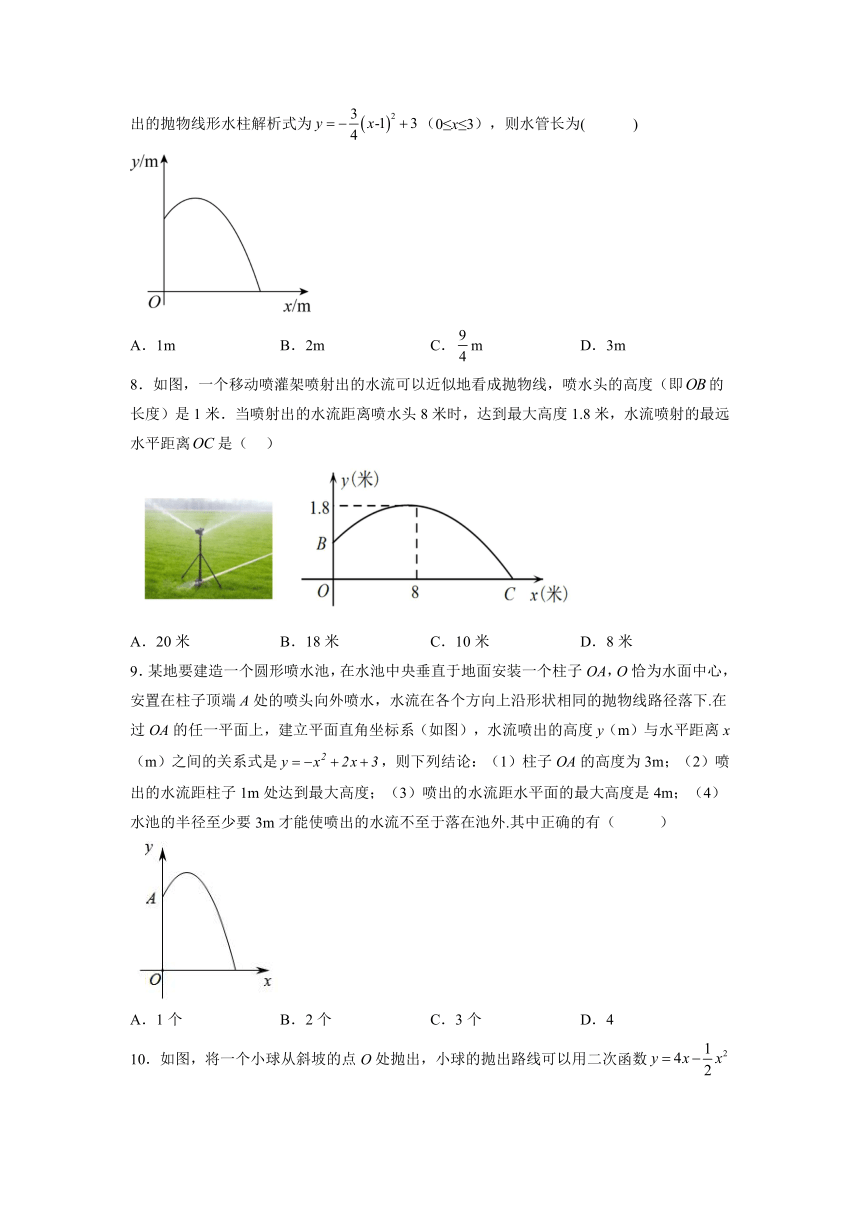
7.在某圆形喷水池的池中心竖直安装一根水管,在水管的顶端安一个喷水头,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,建立如图所示的平面直角坐标系,若喷出的抛物线形水柱解析式为(0≤x≤3),则水管长为( )
A.1m B.2m C.m D.3m
8.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
9.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有( )
A.1个 B.2个 C.3个 D.4
10.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数刻画,斜坡可以用一次函数刻画.下列结论错误的是( )
A.小球落地点距O点水平距离为7米
B.小球距O点水平距离超过4米呈下降趋势
C.当小球抛出高度达到7.5m时,小球距O点水平距离为3m
D.小球距斜坡的最大铅直高度为
二、填空题(共10个小题)
11.某商品的销售利润y与销售单价x的关系为y=+2650,则当x=_______元时,y有最_______值,这个值为______元.
12.某果园有100棵苹果树,平均每棵树可结660个苹果,根据经验估计,在这个果园里每多种一棵树,平均每棵树就会少结6个苹果,则果园里增__________棵苹果树,所结苹果的总数最多.
13.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤24,且x为整数)出售,可卖出(30﹣x)件.若利润为y,则y关于x的解析式___________________,若利润最大,则最大利润为______元.
14.如图,若被击打的小球飞行高度(单位:m)与飞行时间t(单位:s)之间具有的关系为,则小球从飞出到落地所用的时间为______s.
15.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为___________s时,小球达到最高点.
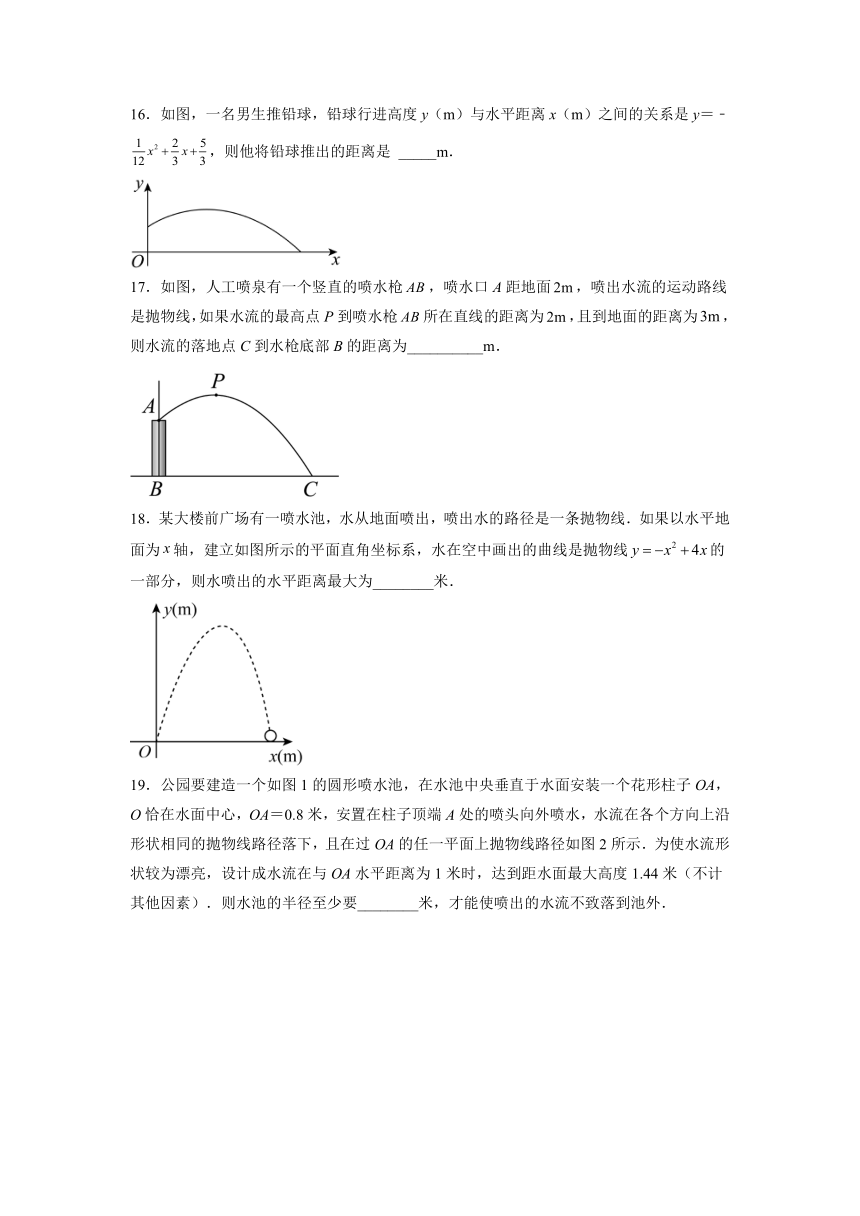
16.如图,一名男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=﹣,则他将铅球推出的距离是 _____m.
17.如图,人工喷泉有一个竖直的喷水枪,喷水口A距地面,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪所在直线的距离为,且到地面的距离为,则水流的落地点C到水枪底部B的距离为__________m.
18.某大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为轴,建立如图所示的平面直角坐标系,水在空中画出的曲线是抛物线的一部分,则水喷出的水平距离最大为________米.
19.公园要建造一个如图1的圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,OA=0.8米,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上抛物线路径如图2所示.为使水流形状较为漂亮,设计成水流在与OA水平距离为1米时,达到距水面最大高度1.44米(不计其他因素).则水池的半径至少要________米,才能使喷出的水流不致落到池外.
20.某游乐园有一圆形喷水池(如图),中心立柱AM上有一喷水头A,其喷出的水柱距池中心3米处达到最高,最远落点到中心M的距离为9米,距立柱4米处地面上有一射灯C,现将喷水头A向上移动1.5米至点B(其余条件均不变),若此时水柱最高处D与A,C在同一直线上,则水柱最远落点到中心M的距离增加了___________米.
三、解答题(共3个小题)
21.某市城建公司新建了一个购物中心,共有商铺30间,据调查分析,当每间的年租金为10万元时,可全部租出,若每间的年租金每增加1万元,则少租出商铺2间,为提供优质服务,城建公司引入物业公司代为管理,租出的商铺每间每年需向物业公司缴纳物业费1万元,未租出的商铺不需要向物业公司缴纳物业费.
(1)当每间商铺的年租金定为多少万元时,该公司的年收益最大,最大收益为多少?
(2)当每间商铺的年租金满足什么条件时,该公司的年收益不低于280万元?
22.掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为,当水平距离为3m时,实心球行进至最高点3m处.
(1)求y关于x的函数表达式;
(2)根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
23.如图1,灌溉车沿着平行于绿化带底部边线的方向行驶,为绿化带浇水.喷水口离地竖直高度为(单位:).如图2,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形,其水平宽度,竖直高度为的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点离喷水口的水平距离为,高出喷水口,灌溉车到的距离为(单位:).
(1)若,;
①求上边缘抛物线的函数解析式,并求喷出水的最大射程;
②求下边缘抛物线与轴的正半轴交点的坐标;
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求的取值范围;
(2)若.要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出的最小值.
22.3.2 销售、投球、喷水问题解析
1.
【答案】C
【详解】解:设每件商品降价x元,每天的销售额为y元.
依题意有:
y=(35﹣x)(50+2x)
=﹣2x2+20x+1750
=﹣2(x﹣5)2+1800,
∵﹣2<0,
∴当x=5时,y最大,最大值为1800,
∴最大销售额为1800元.
故选:C.
2.
【答案】C
【详解】解:设总利润为y元,
∵第档次产品比最低档次产品提高了个档次,
∴每天利润为,
∴当时,产品利润最大,每天获利864元,
故选C.
3.
【答案】D
【详解】解:y=-2x2+60x+800=-2(x-15)2+1250
∵-2<0
故当x=15时,y有最大值,最大值为1250
即利润获得最多为1250元
故选:D.
4.
【答案】B
【详解】解:此炮弹在第秒与第秒时的高度相等,
抛物线的对称轴是:,
炮弹所在高度最高时:
时间是第8.5秒,
最接近,
故选B.
5.
【答案】C
【详解】解:h=30t﹣5t2=﹣5(t﹣3)2+45,
∵﹣5<0,0≤t≤6,
∴当t=3时,h有最大值,最大值为45,
∴小球运动3秒时,小球最高,
故选:C.
6.
【答案】C
【详解】解:∵抛物线形水柱,其解析式为y=﹣(x﹣2)2+6,
∵a=-1<0
∴当x=2时,水柱的最大高度是:6.
故选C.
7.
【答案】C
【详解】解:函数解析式
令,则
则水管的长度为
故选:C.
8.
【答案】A
【详解】解:∵喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,
设抛物线解析式为,将点代入,得
解得
∴抛物线解析式为
令,解得(负值舍去)
即,
故选:A
9.
【答案】D
【详解】解:当x=0时,y=3,故柱子OA的高度为3m;(1)正确;
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点是(1,4),
故喷出的水流距柱子1m处达到最大高度,喷出的水流距水平面的最大高度是4米;故(2)(3)正确;
解方程-x2+2x+3=0,
得x1=-1,x2=3,
故水池的半径至少要3米,才能使喷出的水流不至于落在水池外,(4)正确.
故选D.
10.
【答案】C
【详解】解:联立两函数解析式,得
,解得:或,
则小球落地点距O点水平距离为7米,
故A选项不符合题意;
∵,
则抛物线的对称轴为x=4,
∵<0,
∴当x>4时,y随x的增大而减小,
即小球距O点水平距离超过4米呈下降趋势,
故B选项不符合题意;
当y=7.5时,7.5=4x-x2,
整理得x2-8x+15=0,
解得,x1=3,x2=5,
∴当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m或5m,故此选项符合题意;
如图,设抛物线上一点A(x, 4x-x2),过点A作AB⊥x轴于C,交直线y=x于B,
∴B(x,),
∴AB=4x-x2-=-x2x=-(x-)2+,
∵<0,
∴当x=时,AB有最大值,最大值=,
即小球距斜坡的最大铅直高度为,
故D选项不符合题意.
故选:C.
11.
【答案】 50 大 2650
【详解】解:∵<0,
∴抛物线开口向下,
∵销售利润y与销售单价x的关系为y=﹣+2650,
∴当单价定价为每件50元时,可获得最大利润2650元.
故答案为:50,大,2650.
12.
【答案】5
【详解】解:设果园里增x棵苹果树,所结苹果的总数为y,
根据题意得y=(100+x)(660﹣6x)
=﹣6x2+60x+66000
=﹣6(x﹣5)2+66150,
∵a=﹣6,
∴当x=5时,y有最大值66150,
即果园里增5棵苹果树,所结苹果的总数最多.
故答案为5.
13.
【答案】 y=﹣(x﹣25)2+25 24
【详解】解:设最大利润为元,
则,
∵20≤x≤24,
当时,二次函数有最大值24,
故答案是:;24.
14.
【答案】5
【详解】解:由题意可知,当时,,
整理得,解得或,
小球飞出时间为s,落地时间为s,
小球从飞出到落地所用的时间为s,
故答案为:.
15.
【答案】2
【详解】根据题意,有,
当时,有最大值.
故答案为:2.
16.
【答案】10
【详解】解:当y=0时,-=0,
解之得x1=10,x2=-2(不合题意,舍去),
所以推铅球的距离是10米.
故答案为10
17.
【答案】
【详解】解:如图,以所在直线为轴、所在直线为轴建立直角坐标系,
由题意知,抛物线的顶点的坐标为、点,
设抛物线的解析式为,
将点代入,得:,
解得:,
则抛物线的解析式为:,
当时,有,
解得:(舍或,
m,
答:水流的落地点到水枪底部的距离为.
故答案为:.
18.
【答案】4
【详解】解:∵喷出水的路径是抛物线,
∴水喷出的最大水平距离为抛物线顶点横坐标的2倍.
∵,
∴顶点坐标为(2,4).
∴水喷出的最大水平距离为:(千米).
故答案为:4.
19.
【答案】2.5
【详解】根据题意可得抛物线的顶点坐标为,且图象过点,
,
,
,则,
当时,,即,
解得,(舍去),故水池半径至少为2.5米.
故答案为:2.5.
20.
【答案】
【详解】解:如图,以地面为x轴,中心立柱为y轴建立平面直角坐标系.
根据题意可知水柱可以看成抛物线(只考虑第一象限).
由题意可知C点坐标为(-4,0).
∵喷水头A喷出的水柱距池中心3米处达到最高,
故该抛物线的对称轴为.
∴设该抛物线解析式为,
又∵水柱最远落点到中心M的距离为9米,
∴该抛物线又经过点(9,0).
∴,即,
∴该抛物线解析式为.
当x=0时,
故点A坐标为(0,-27a).
由题意可知将喷水头A向上移动1.5米至点B,即将抛物线向上平移1.5.
∴平移后的抛物线为.
∴点D坐标为(3,).
设经过点A、C的直线解析式为,
∴,解得.
即经过点A、C的直线解析式为.
又∵该直线经过点D.
∴.
解得:.
故平移后的抛物线解析式为,
整理得:.
当时,即,
解得:(舍).
∴移动后最远落点到中心M的距离为米,
∴移动后水柱最远落点到中心M的距离增加了(米).
故答案为:.
21.
【答案】(1)当每间商铺的年租金定为13万元时,该公司的年收益最大,最大收益为288万元
(2)当每间商铺的年租金定在11到15万元时(含11万和15万),该公司的年收益不低于280万元.
【详解】(1)解:(1)设每间商铺的年租金定比10万增加x万元时,该公司的年收益为 万元,
根据题意得,出租的商铺数量为,且,
∴,
∵,
∴
∵﹣2<0,抛物线的开口向下,
∴当x=3时,y有最大值,最大值为288,此时,年租金为13万元,
答:当每间商铺的年租金定为13万元时,该公司的年收益最大,最大收益为288万元;
(2)由(1)得,
当时,,
∴,
∴,
由于抛物线开口向下,
∴当时,,
∴当每间商铺的年租金定在11到15万元时(含11万和15万),该公司的年收益不低于280万元.
22.
【答案】(1)y关于x的函数表达式为;
(2)该女生在此项考试中是得满分,理由见解析.
【详解】(1)解∶∵当水平距离为3m时,实心球行进至最高点3m处,
∴设,
∵经过点(0, ),
∴
解得∶
∴,
∴y关于x的函数表达式为;
(2)解:该女生在此项考试中是得满分,理由如下∶
∵对于二次函数,当y=0时,有
∴,
解得∶, (舍去),
∵>6.70,
∴该女生在此项考试中是得满分.
23.
【答案】(1)①,;②;③;(2)
【详解】(1)(1)①如图1,由题意得是上边缘抛物线的顶点,
设.
又∵抛物线经过点,
∴,
∴.
∴上边缘抛物线的函数解析式为.
当时,,
∴,(舍去).
∴喷出水的最大射程为.
图1
②∵对称轴为直线,
∴点的对称点的坐标为.
∴下边缘抛物线是由上边缘抛物线向左平移得到的,
即点是由点向左平移得到,则点的坐标为.
③如图2,先看上边缘抛物线,
∵,
∴点的纵坐标为0.5.
抛物线恰好经过点时,
.
解得,
∵,
∴.
当时,随着的增大而减小,
∴当时,要使,
则.
∵当时,随的增大而增大,且时,,
∴当时,要使,则.
∵,灌溉车喷出的水要浇灌到整个绿化带,
∴的最大值为.
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是,
∴的最小值为2.
综上所述,的取值范围是.
(2)的最小值为.
由题意得是上边缘抛物线的顶点,
∴设上边缘抛物线解析式为.
∵上边缘抛物线过出水口(0,h)
∴
解得
∴上边缘抛物线解析式为
∵对称轴为直线,
∴点的对称点的坐标为.
∴下边缘抛物线是由上边缘抛物线向左平移得到的,
∴下边缘抛物线解析式为.
当喷水口高度最低,且恰好能浇灌到整个绿化带时,点,恰好分别在两条抛物线上,
∵DE=3
∴设点,,,
∵D在下边缘抛物线上,
∴
∵EF=1
∴
∴,
解得,
代入,得.
所以的最小值为.
一、单选题(共10个小题)
1.某商品现在的售价为每件35元,每天可卖出50件.市场调查反映:如果调整价格,每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,求最大销售额是( )
A.2500元 B.2000元 C.1800元 D.2200元
2.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量増加),那么等于( )
A. B. C. D.
3.某商场降价销售一批名牌衬衫,已知所获利润y(元)与降价x(元)之间的关系是y=-2x2+60x+800,则利润获得最多为( )
A.15元 B.400元 C.800元 D.1250元
4.向上发射一枚炮弹,经秒后的高度为公尺,且时间秒与高度公尺的关系为、为常数,且若此炮弹在第秒与第秒时的高度相等,则下列哪一个时间的高度是最高的?( )
A.第秒 B.第秒 C.第秒 D.第秒
5.从地面竖直向上抛出一小球,小球的高度h(米)与运动时间t(秒)之间的关系式是h=30t﹣5t2(0≤t≤6),则小球最高时,运动的时间是( )
A.1秒 B.2秒 C.3秒 D.4秒
6.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=﹣(x﹣2)2+6,则水柱的最大高度是( )
A.2 B.4 C.6 D.2+
7.在某圆形喷水池的池中心竖直安装一根水管,在水管的顶端安一个喷水头,以水管与地面交点为原点,原点与水柱落地处所在直线为x轴,建立如图所示的平面直角坐标系,若喷出的抛物线形水柱解析式为(0≤x≤3),则水管长为( )
A.1m B.2m C.m D.3m
8.如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,水流喷射的最远水平距离是( )
A.20米 B.18米 C.10米 D.8米
9.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有( )
A.1个 B.2个 C.3个 D.4
10.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数刻画,斜坡可以用一次函数刻画.下列结论错误的是( )
A.小球落地点距O点水平距离为7米
B.小球距O点水平距离超过4米呈下降趋势
C.当小球抛出高度达到7.5m时,小球距O点水平距离为3m
D.小球距斜坡的最大铅直高度为
二、填空题(共10个小题)
11.某商品的销售利润y与销售单价x的关系为y=+2650,则当x=_______元时,y有最_______值,这个值为______元.
12.某果园有100棵苹果树,平均每棵树可结660个苹果,根据经验估计,在这个果园里每多种一棵树,平均每棵树就会少结6个苹果,则果园里增__________棵苹果树,所结苹果的总数最多.
13.某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤24,且x为整数)出售,可卖出(30﹣x)件.若利润为y,则y关于x的解析式___________________,若利润最大,则最大利润为______元.
14.如图,若被击打的小球飞行高度(单位:m)与飞行时间t(单位:s)之间具有的关系为,则小球从飞出到落地所用的时间为______s.
15.根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是,当飞行时间t为___________s时,小球达到最高点.
16.如图,一名男生推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=﹣,则他将铅球推出的距离是 _____m.
17.如图,人工喷泉有一个竖直的喷水枪,喷水口A距地面,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪所在直线的距离为,且到地面的距离为,则水流的落地点C到水枪底部B的距离为__________m.
18.某大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.如果以水平地面为轴,建立如图所示的平面直角坐标系,水在空中画出的曲线是抛物线的一部分,则水喷出的水平距离最大为________米.
19.公园要建造一个如图1的圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,OA=0.8米,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上抛物线路径如图2所示.为使水流形状较为漂亮,设计成水流在与OA水平距离为1米时,达到距水面最大高度1.44米(不计其他因素).则水池的半径至少要________米,才能使喷出的水流不致落到池外.
20.某游乐园有一圆形喷水池(如图),中心立柱AM上有一喷水头A,其喷出的水柱距池中心3米处达到最高,最远落点到中心M的距离为9米,距立柱4米处地面上有一射灯C,现将喷水头A向上移动1.5米至点B(其余条件均不变),若此时水柱最高处D与A,C在同一直线上,则水柱最远落点到中心M的距离增加了___________米.
三、解答题(共3个小题)
21.某市城建公司新建了一个购物中心,共有商铺30间,据调查分析,当每间的年租金为10万元时,可全部租出,若每间的年租金每增加1万元,则少租出商铺2间,为提供优质服务,城建公司引入物业公司代为管理,租出的商铺每间每年需向物业公司缴纳物业费1万元,未租出的商铺不需要向物业公司缴纳物业费.
(1)当每间商铺的年租金定为多少万元时,该公司的年收益最大,最大收益为多少?
(2)当每间商铺的年租金满足什么条件时,该公司的年收益不低于280万元?
22.掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为,当水平距离为3m时,实心球行进至最高点3m处.
(1)求y关于x的函数表达式;
(2)根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
23.如图1,灌溉车沿着平行于绿化带底部边线的方向行驶,为绿化带浇水.喷水口离地竖直高度为(单位:).如图2,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形,其水平宽度,竖直高度为的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点离喷水口的水平距离为,高出喷水口,灌溉车到的距离为(单位:).
(1)若,;
①求上边缘抛物线的函数解析式,并求喷出水的最大射程;
②求下边缘抛物线与轴的正半轴交点的坐标;
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求的取值范围;
(2)若.要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出的最小值.
22.3.2 销售、投球、喷水问题解析
1.
【答案】C
【详解】解:设每件商品降价x元,每天的销售额为y元.
依题意有:
y=(35﹣x)(50+2x)
=﹣2x2+20x+1750
=﹣2(x﹣5)2+1800,
∵﹣2<0,
∴当x=5时,y最大,最大值为1800,
∴最大销售额为1800元.
故选:C.
2.
【答案】C
【详解】解:设总利润为y元,
∵第档次产品比最低档次产品提高了个档次,
∴每天利润为,
∴当时,产品利润最大,每天获利864元,
故选C.
3.
【答案】D
【详解】解:y=-2x2+60x+800=-2(x-15)2+1250
∵-2<0
故当x=15时,y有最大值,最大值为1250
即利润获得最多为1250元
故选:D.
4.
【答案】B
【详解】解:此炮弹在第秒与第秒时的高度相等,
抛物线的对称轴是:,
炮弹所在高度最高时:
时间是第8.5秒,
最接近,
故选B.
5.
【答案】C
【详解】解:h=30t﹣5t2=﹣5(t﹣3)2+45,
∵﹣5<0,0≤t≤6,
∴当t=3时,h有最大值,最大值为45,
∴小球运动3秒时,小球最高,
故选:C.
6.
【答案】C
【详解】解:∵抛物线形水柱,其解析式为y=﹣(x﹣2)2+6,
∵a=-1<0
∴当x=2时,水柱的最大高度是:6.
故选C.
7.
【答案】C
【详解】解:函数解析式
令,则
则水管的长度为
故选:C.
8.
【答案】A
【详解】解:∵喷水头的高度(即的长度)是1米.当喷射出的水流距离喷水头8米时,达到最大高度1.8米,
设抛物线解析式为,将点代入,得
解得
∴抛物线解析式为
令,解得(负值舍去)
即,
故选:A
9.
【答案】D
【详解】解:当x=0时,y=3,故柱子OA的高度为3m;(1)正确;
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点是(1,4),
故喷出的水流距柱子1m处达到最大高度,喷出的水流距水平面的最大高度是4米;故(2)(3)正确;
解方程-x2+2x+3=0,
得x1=-1,x2=3,
故水池的半径至少要3米,才能使喷出的水流不至于落在水池外,(4)正确.
故选D.
10.
【答案】C
【详解】解:联立两函数解析式,得
,解得:或,
则小球落地点距O点水平距离为7米,
故A选项不符合题意;
∵,
则抛物线的对称轴为x=4,
∵<0,
∴当x>4时,y随x的增大而减小,
即小球距O点水平距离超过4米呈下降趋势,
故B选项不符合题意;
当y=7.5时,7.5=4x-x2,
整理得x2-8x+15=0,
解得,x1=3,x2=5,
∴当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m或5m,故此选项符合题意;
如图,设抛物线上一点A(x, 4x-x2),过点A作AB⊥x轴于C,交直线y=x于B,
∴B(x,),
∴AB=4x-x2-=-x2x=-(x-)2+,
∵<0,
∴当x=时,AB有最大值,最大值=,
即小球距斜坡的最大铅直高度为,
故D选项不符合题意.
故选:C.
11.
【答案】 50 大 2650
【详解】解:∵<0,
∴抛物线开口向下,
∵销售利润y与销售单价x的关系为y=﹣+2650,
∴当单价定价为每件50元时,可获得最大利润2650元.
故答案为:50,大,2650.
12.
【答案】5
【详解】解:设果园里增x棵苹果树,所结苹果的总数为y,
根据题意得y=(100+x)(660﹣6x)
=﹣6x2+60x+66000
=﹣6(x﹣5)2+66150,
∵a=﹣6,
∴当x=5时,y有最大值66150,
即果园里增5棵苹果树,所结苹果的总数最多.
故答案为5.
13.
【答案】 y=﹣(x﹣25)2+25 24
【详解】解:设最大利润为元,
则,
∵20≤x≤24,
当时,二次函数有最大值24,
故答案是:;24.
14.
【答案】5
【详解】解:由题意可知,当时,,
整理得,解得或,
小球飞出时间为s,落地时间为s,
小球从飞出到落地所用的时间为s,
故答案为:.
15.
【答案】2
【详解】根据题意,有,
当时,有最大值.
故答案为:2.
16.
【答案】10
【详解】解:当y=0时,-=0,
解之得x1=10,x2=-2(不合题意,舍去),
所以推铅球的距离是10米.
故答案为10
17.
【答案】
【详解】解:如图,以所在直线为轴、所在直线为轴建立直角坐标系,
由题意知,抛物线的顶点的坐标为、点,
设抛物线的解析式为,
将点代入,得:,
解得:,
则抛物线的解析式为:,
当时,有,
解得:(舍或,
m,
答:水流的落地点到水枪底部的距离为.
故答案为:.
18.
【答案】4
【详解】解:∵喷出水的路径是抛物线,
∴水喷出的最大水平距离为抛物线顶点横坐标的2倍.
∵,
∴顶点坐标为(2,4).
∴水喷出的最大水平距离为:(千米).
故答案为:4.
19.
【答案】2.5
【详解】根据题意可得抛物线的顶点坐标为,且图象过点,
,
,
,则,
当时,,即,
解得,(舍去),故水池半径至少为2.5米.
故答案为:2.5.
20.
【答案】
【详解】解:如图,以地面为x轴,中心立柱为y轴建立平面直角坐标系.
根据题意可知水柱可以看成抛物线(只考虑第一象限).
由题意可知C点坐标为(-4,0).
∵喷水头A喷出的水柱距池中心3米处达到最高,
故该抛物线的对称轴为.
∴设该抛物线解析式为,
又∵水柱最远落点到中心M的距离为9米,
∴该抛物线又经过点(9,0).
∴,即,
∴该抛物线解析式为.
当x=0时,
故点A坐标为(0,-27a).
由题意可知将喷水头A向上移动1.5米至点B,即将抛物线向上平移1.5.
∴平移后的抛物线为.
∴点D坐标为(3,).
设经过点A、C的直线解析式为,
∴,解得.
即经过点A、C的直线解析式为.
又∵该直线经过点D.
∴.
解得:.
故平移后的抛物线解析式为,
整理得:.
当时,即,
解得:(舍).
∴移动后最远落点到中心M的距离为米,
∴移动后水柱最远落点到中心M的距离增加了(米).
故答案为:.
21.
【答案】(1)当每间商铺的年租金定为13万元时,该公司的年收益最大,最大收益为288万元
(2)当每间商铺的年租金定在11到15万元时(含11万和15万),该公司的年收益不低于280万元.
【详解】(1)解:(1)设每间商铺的年租金定比10万增加x万元时,该公司的年收益为 万元,
根据题意得,出租的商铺数量为,且,
∴,
∵,
∴
∵﹣2<0,抛物线的开口向下,
∴当x=3时,y有最大值,最大值为288,此时,年租金为13万元,
答:当每间商铺的年租金定为13万元时,该公司的年收益最大,最大收益为288万元;
(2)由(1)得,
当时,,
∴,
∴,
由于抛物线开口向下,
∴当时,,
∴当每间商铺的年租金定在11到15万元时(含11万和15万),该公司的年收益不低于280万元.
22.
【答案】(1)y关于x的函数表达式为;
(2)该女生在此项考试中是得满分,理由见解析.
【详解】(1)解∶∵当水平距离为3m时,实心球行进至最高点3m处,
∴设,
∵经过点(0, ),
∴
解得∶
∴,
∴y关于x的函数表达式为;
(2)解:该女生在此项考试中是得满分,理由如下∶
∵对于二次函数,当y=0时,有
∴,
解得∶, (舍去),
∵>6.70,
∴该女生在此项考试中是得满分.
23.
【答案】(1)①,;②;③;(2)
【详解】(1)(1)①如图1,由题意得是上边缘抛物线的顶点,
设.
又∵抛物线经过点,
∴,
∴.
∴上边缘抛物线的函数解析式为.
当时,,
∴,(舍去).
∴喷出水的最大射程为.
图1
②∵对称轴为直线,
∴点的对称点的坐标为.
∴下边缘抛物线是由上边缘抛物线向左平移得到的,
即点是由点向左平移得到,则点的坐标为.
③如图2,先看上边缘抛物线,
∵,
∴点的纵坐标为0.5.
抛物线恰好经过点时,
.
解得,
∵,
∴.
当时,随着的增大而减小,
∴当时,要使,
则.
∵当时,随的增大而增大,且时,,
∴当时,要使,则.
∵,灌溉车喷出的水要浇灌到整个绿化带,
∴的最大值为.
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是,
∴的最小值为2.
综上所述,的取值范围是.
(2)的最小值为.
由题意得是上边缘抛物线的顶点,
∴设上边缘抛物线解析式为.
∵上边缘抛物线过出水口(0,h)
∴
解得
∴上边缘抛物线解析式为
∵对称轴为直线,
∴点的对称点的坐标为.
∴下边缘抛物线是由上边缘抛物线向左平移得到的,
∴下边缘抛物线解析式为.
当喷水口高度最低,且恰好能浇灌到整个绿化带时,点,恰好分别在两条抛物线上,
∵DE=3
∴设点,,,
∵D在下边缘抛物线上,
∴
∵EF=1
∴
∴,
解得,
代入,得.
所以的最小值为.
同课章节目录
