12.1全等三角形课件
图片预览





文档简介
课件20张PPT。 全等三角形12.1 学习目标:
1、理解全等形、全等三角形的概念;
2、能识别全等三角形的对应顶点、对应边、对应角;
3、掌握并能运用全等三角形的性质。自学 提示 内容:课本第31页----第32页
时间:3分钟
要求:1、圈画出全等形、全等三角形的定义;
2、找出全等三角形的表示方法;
3、了解全等三角形的性质及应用。
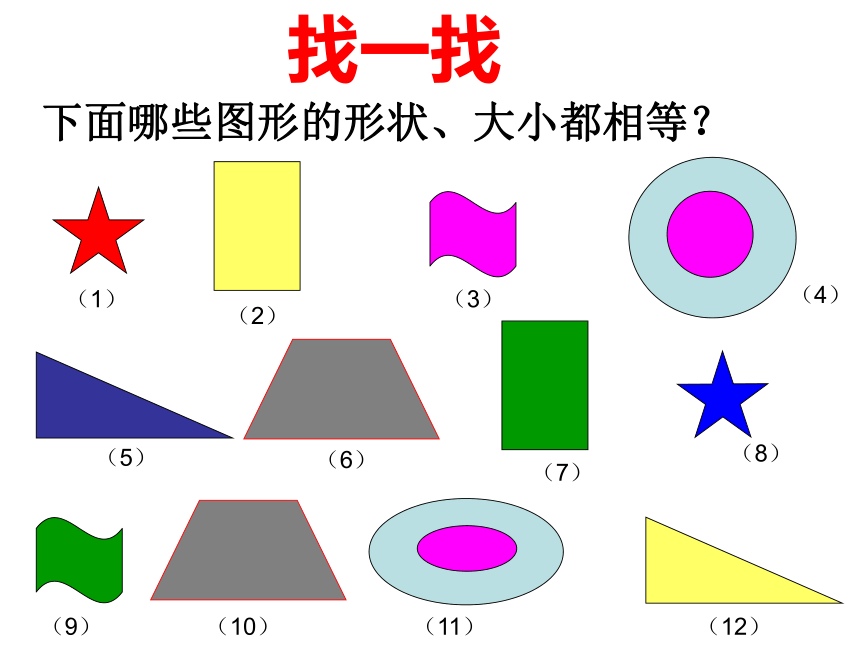
形式: 自己独立学习下面哪些图形的形状、大小都相等? 找一找(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12) 举出现实生活中能够完全重合的图形的例子。说一说
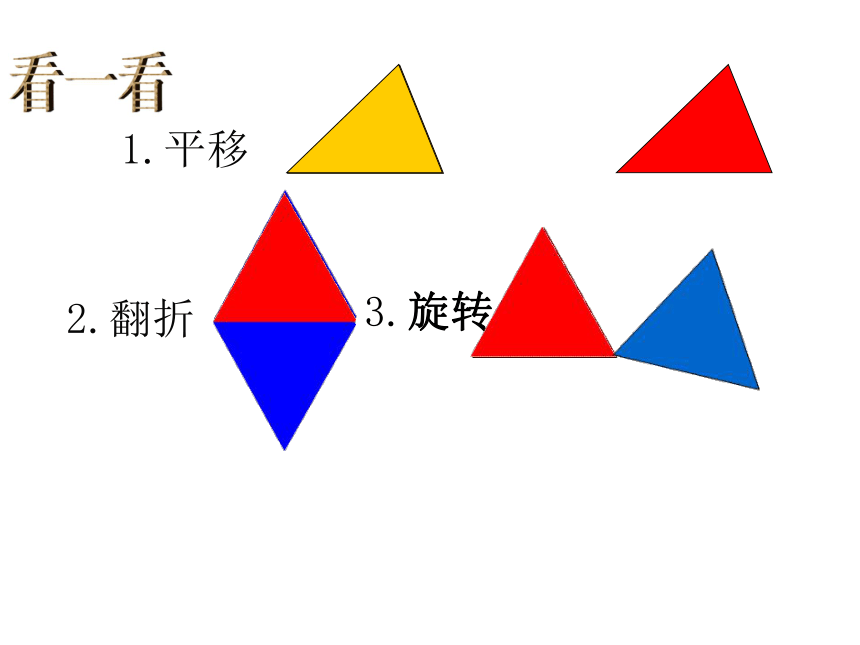
全等形:能够完全重合的两个图形叫做全等形。 将一块三角板按在纸板上,画下图形,照样裁下纸板。裁下的纸板和样板的形状、大小是否 完 全 一样?能完全重合吗? 全等三角形:能够完全重合的两个三角形。 1.平移2.翻折看一看3.旋转 一个图形经过平移,翻折,旋转后,位置变化了,但___和___都没有改变,即平移,翻折,旋转前后的图形__。形状大小全等根据刚才你看到的图形的变化回答:互相重合的边叫做对应边。互相重合的顶点叫做对应顶点。互相重合的角叫做对应角。AB与DEBC与EFAC与DF∠A与∠D∠B与∠E∠C与∠F “全等”用符号“≌ ”,表示图中的△ABC和△DEF全等, 全等三角形的表示方法记作△ABC≌ △DEF,读作△ABC全等于△DEF注意记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。 如图:△ABC≌ △DEF,这两个三角形的对应边有什么关系?对应角呢?思 考:如图:∵△ABC≌△DEF∴A B=D E,A C=D F,B C=E F(对应边相等)全等三角形的性质: 全等三角形的对应边相等;
全等三角形的对应角相等.∠A=∠D,∠B=∠E,∠C=∠F( 对应角相等) 几何语言
例1:如图,?ACO绕O旋转1800,得到?BOD.O则:
?ACO ?BOD
OA OB,
OC= ,
∠A= ,
∠D= ,
∠AOC与 是对应角
全等三角形性质的应用 例2:如图,△ABC≌△AEC,∠B=30°,∠ACB=85°.求出△AEC各内角的度数.全等三角形性质的应用解:∵△ABC≌△AEC∴∠E =∠B=30°,∠ACE =∠ACB=85° 在△AEC 中
∠EAC = 180°─ 85°─ 30°= 65°答:△AEC的内角的度数分别为65°、30°、85°
通过本节课的学习,你有什么收获? 全等三角形全等形的定义:能够完全重合的两个图形叫做全等形.定义:能够完全重合的两个三角形叫做全等三角形.表示方法:△ABC≌△DEF
(对应点要写在对应的位置上).性质:对应边相等,对应角相等.会用全等三角形的性质解决简单的问题.畅所欲言
一、选择题如图:△ABC≌ △BAD,如果AB=5cm, BD=4cm,AD=6cm,那么BC的长是( )
(A)6cm (B)5cm
(C)4cm ( D)无法确定
在上题中, ∠CAB的对应角是( )
(A)∠DAB (B) ∠ DBA
(C) ∠ DBC (D) ∠ CAD课堂检测课堂检测二、如图:△ABC ≌ △ADE,
若AB=3cm, AC=5cm , ∠ B=50°,∠BAC=85°,
求AD,AE的长度及∠E的度数三、如图△ABC ≌ △DEF,边AB和DE在同一条直线上,试说明图中有哪些线段平行,并说明理由。CDABEF1.必做题:教科书习题12.1 复习巩固第1、2题 、
综合运用第3题
2.选做题:教科书习题12.1拓广探索第5题课后作业,巩固提高
1、理解全等形、全等三角形的概念;
2、能识别全等三角形的对应顶点、对应边、对应角;
3、掌握并能运用全等三角形的性质。自学 提示 内容:课本第31页----第32页
时间:3分钟
要求:1、圈画出全等形、全等三角形的定义;
2、找出全等三角形的表示方法;
3、了解全等三角形的性质及应用。
形式: 自己独立学习下面哪些图形的形状、大小都相等? 找一找(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12) 举出现实生活中能够完全重合的图形的例子。说一说
全等形:能够完全重合的两个图形叫做全等形。 将一块三角板按在纸板上,画下图形,照样裁下纸板。裁下的纸板和样板的形状、大小是否 完 全 一样?能完全重合吗? 全等三角形:能够完全重合的两个三角形。 1.平移2.翻折看一看3.旋转 一个图形经过平移,翻折,旋转后,位置变化了,但___和___都没有改变,即平移,翻折,旋转前后的图形__。形状大小全等根据刚才你看到的图形的变化回答:互相重合的边叫做对应边。互相重合的顶点叫做对应顶点。互相重合的角叫做对应角。AB与DEBC与EFAC与DF∠A与∠D∠B与∠E∠C与∠F “全等”用符号“≌ ”,表示图中的△ABC和△DEF全等, 全等三角形的表示方法记作△ABC≌ △DEF,读作△ABC全等于△DEF注意记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。 如图:△ABC≌ △DEF,这两个三角形的对应边有什么关系?对应角呢?思 考:如图:∵△ABC≌△DEF∴A B=D E,A C=D F,B C=E F(对应边相等)全等三角形的性质: 全等三角形的对应边相等;
全等三角形的对应角相等.∠A=∠D,∠B=∠E,∠C=∠F( 对应角相等) 几何语言
例1:如图,?ACO绕O旋转1800,得到?BOD.O则:
?ACO ?BOD
OA OB,
OC= ,
∠A= ,
∠D= ,
∠AOC与 是对应角
全等三角形性质的应用 例2:如图,△ABC≌△AEC,∠B=30°,∠ACB=85°.求出△AEC各内角的度数.全等三角形性质的应用解:∵△ABC≌△AEC∴∠E =∠B=30°,∠ACE =∠ACB=85° 在△AEC 中
∠EAC = 180°─ 85°─ 30°= 65°答:△AEC的内角的度数分别为65°、30°、85°
通过本节课的学习,你有什么收获? 全等三角形全等形的定义:能够完全重合的两个图形叫做全等形.定义:能够完全重合的两个三角形叫做全等三角形.表示方法:△ABC≌△DEF
(对应点要写在对应的位置上).性质:对应边相等,对应角相等.会用全等三角形的性质解决简单的问题.畅所欲言
一、选择题如图:△ABC≌ △BAD,如果AB=5cm, BD=4cm,AD=6cm,那么BC的长是( )
(A)6cm (B)5cm
(C)4cm ( D)无法确定
在上题中, ∠CAB的对应角是( )
(A)∠DAB (B) ∠ DBA
(C) ∠ DBC (D) ∠ CAD课堂检测课堂检测二、如图:△ABC ≌ △ADE,
若AB=3cm, AC=5cm , ∠ B=50°,∠BAC=85°,
求AD,AE的长度及∠E的度数三、如图△ABC ≌ △DEF,边AB和DE在同一条直线上,试说明图中有哪些线段平行,并说明理由。CDABEF1.必做题:教科书习题12.1 复习巩固第1、2题 、
综合运用第3题
2.选做题:教科书习题12.1拓广探索第5题课后作业,巩固提高
