11.1.2三角形的有关线段课件
文档属性
| 名称 | 11.1.2三角形的有关线段课件 |  | |
| 格式 | zip | ||
| 文件大小 | 484.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-10-23 11:22:40 | ||
图片预览




文档简介
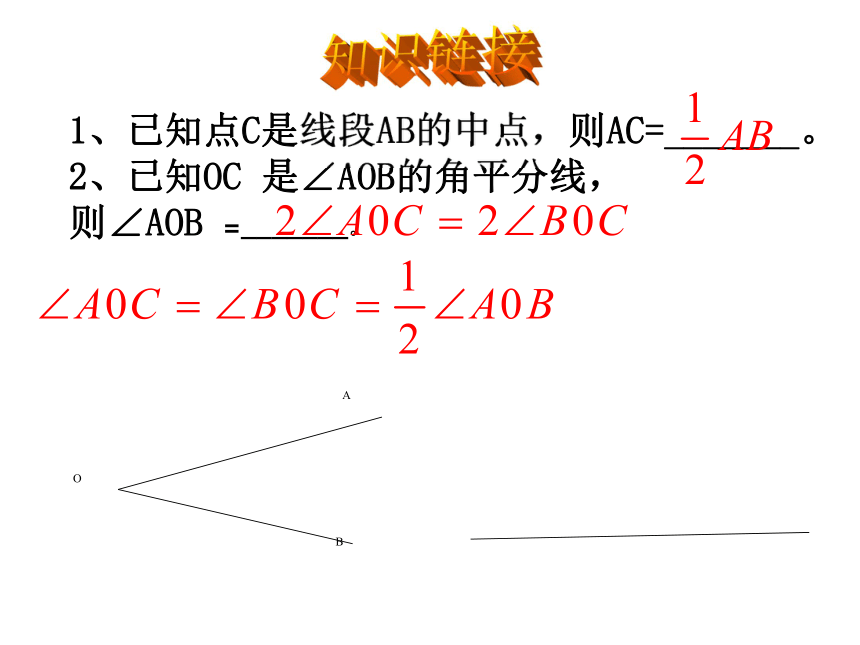
课件42张PPT。11.1.2 三角形的高、中线与角平分线1、已知点C是线段AB的中点,则AC=_______。
2、已知OC 是∠AOB的角平分线,zxxk
则∠AOB =_______。知识链接
你还记得 “过一点画已知
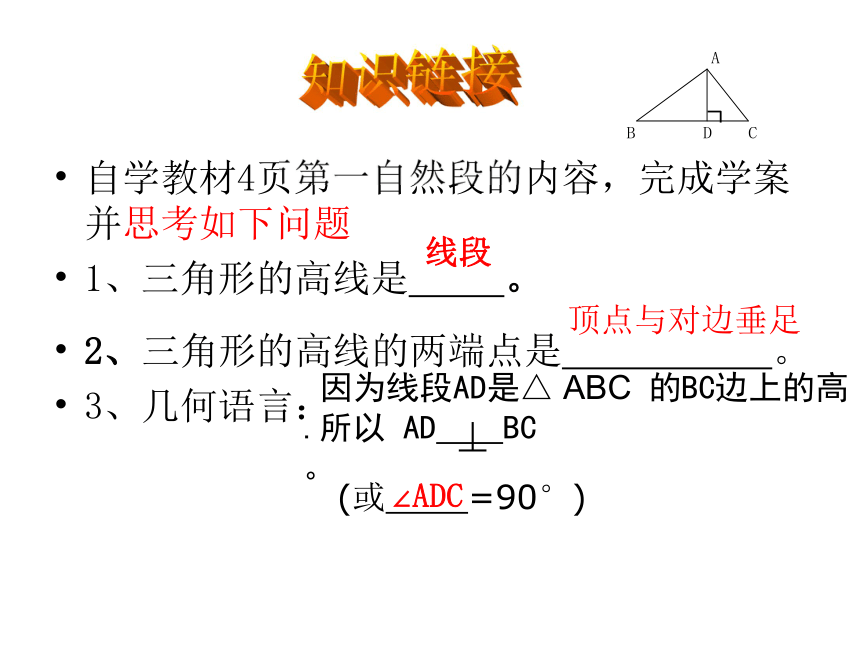
直线的垂线” 吗?自学教材4页第一自然段的内容,完成学案并思考如下问题
1、三角形的高线是 。Z.xxk
2、三角形的高线的两端点是 。
3、几何语言:知识链接
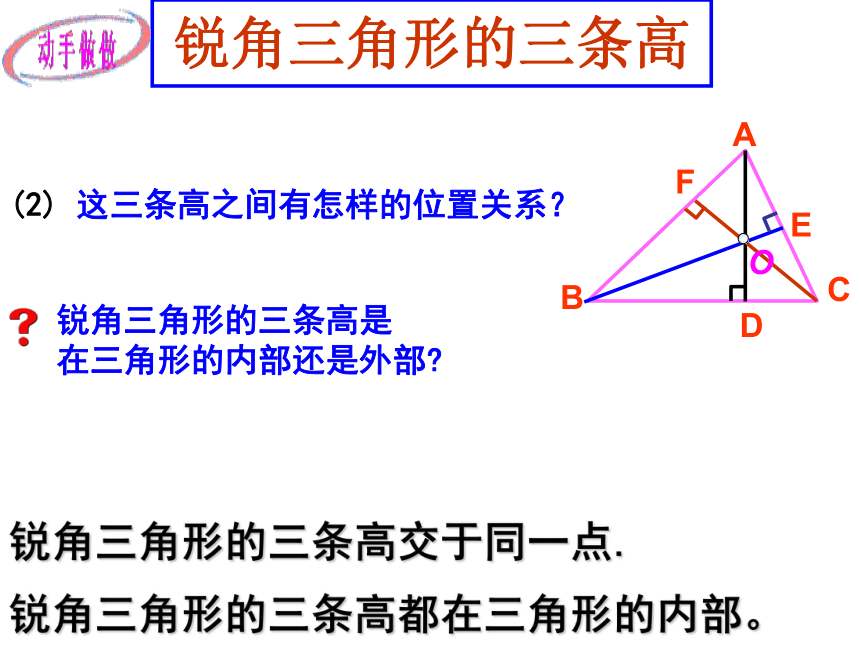
因为线段AD是△ ABC 的BC边上的高.所以 AD BC 。线段顶点与对边垂足(或 =90°) ∠ADC 锐角三角形的三条高(2) 这三条高之间有怎样的位置关系?锐角三角形的三条高是
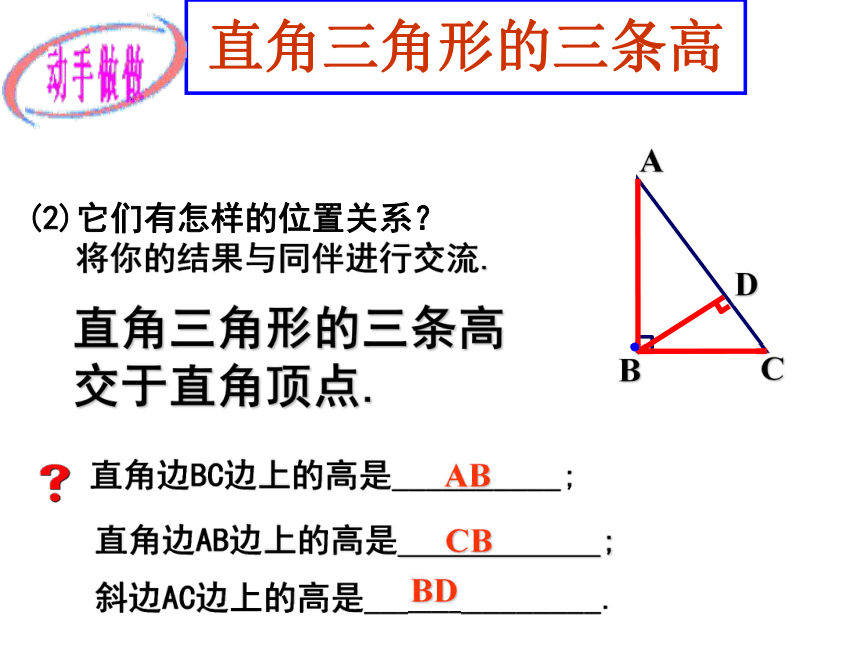
在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部。直角三角形的三条高 将你的结果与同伴进行交流.ABC直角边BC边上的高是__________; AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?D斜边AC边上的高是______________. BD●直角三角形的三条高
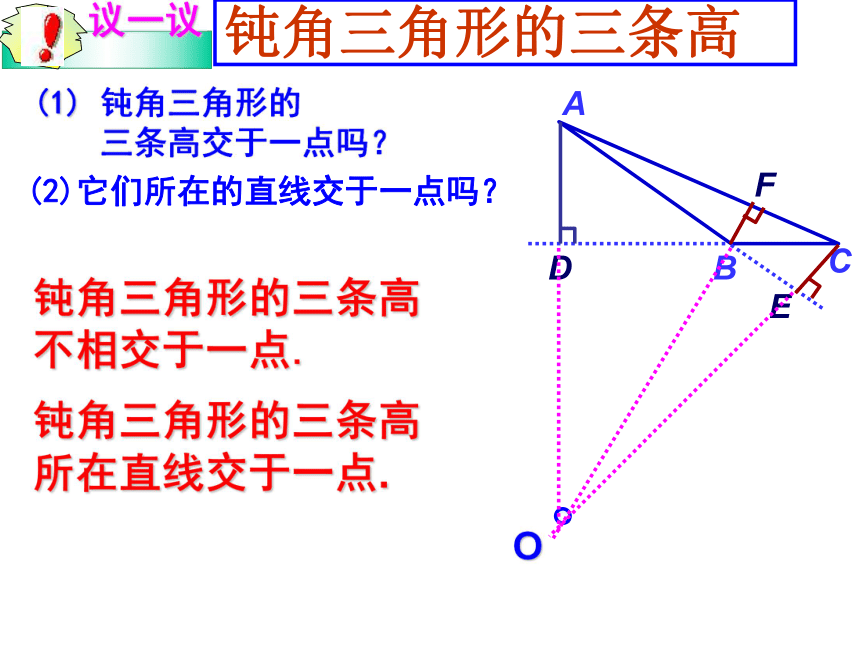
交于直角顶点.钝角三角形的三条高(1) 钝角三角形的
三条高交于一点吗?(2)它们所在的直线交于一点吗?O钝角三角形的三条高
不相交于一点.钝角三角形的三条高
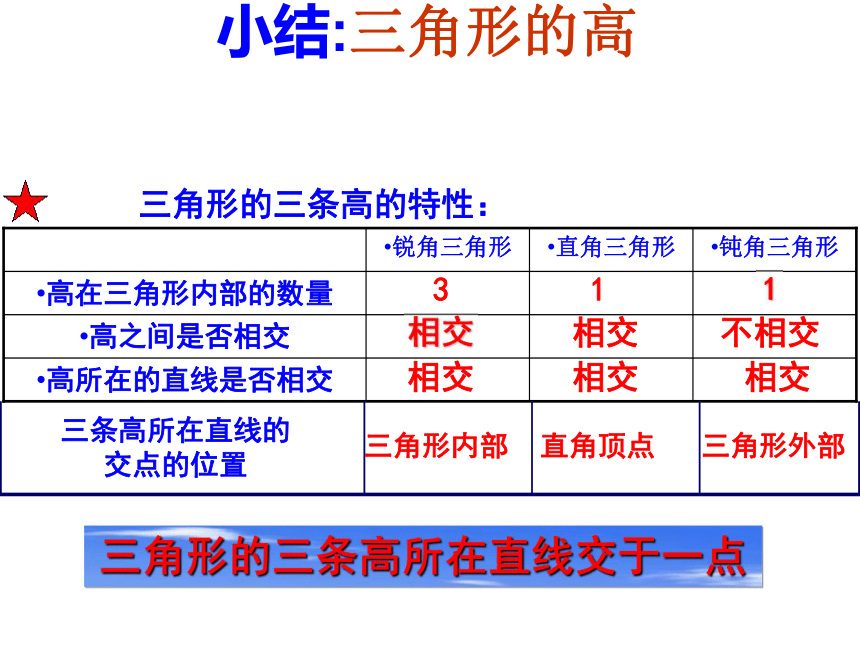
所在直线交于一点.小结:三角形的高311相交相交不相交相交相交相交三角形的三条高所在直线交于一点三角形内部直角顶点三角形外部自学课本4页剩下部分到5页的内容完成学案并思考如下问题
1、三角形的中线是 。
2、三角形的中线的两端点是 。
3、几何语言:
4、锐角三角形、钝角三角形和直角三角形有几条中线?
知识链接
因为线段AD是△ ABC BC边上的中线.所以 。线段顶点与对边中点=导学案
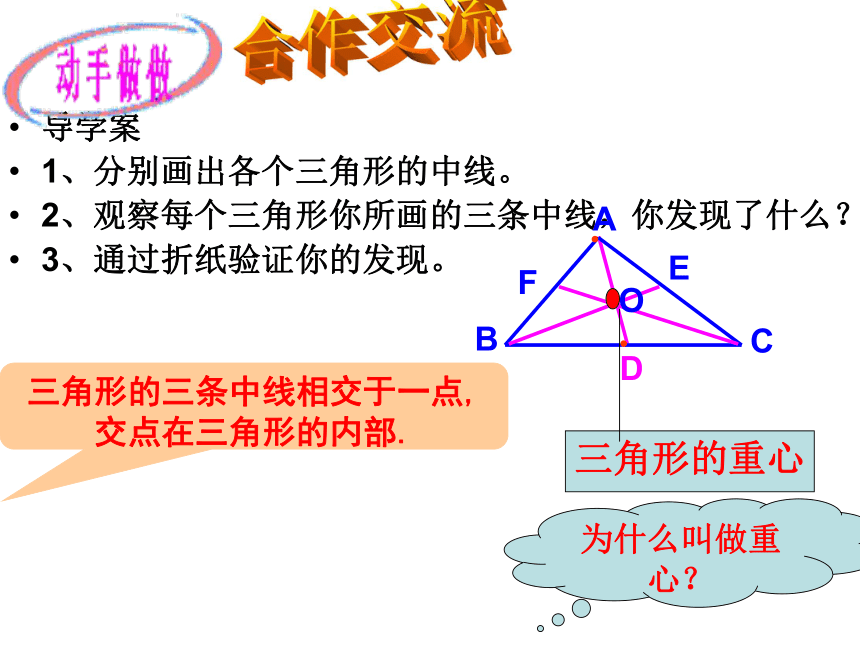
1、分别画出各个三角形的中线。
2、观察每个三角形你所画的三条中线,你发现了什么?
3、通过折纸验证你的发现。Zx.xk
D●●三角形的三条中线相交于一点,交点在三角形的内部.EFO合作交流三角形的重心为什么叫做重心?1、三角形的角平分线是 。
2、三角形的角平分线的两端点是 。
3、几何语言:
4、锐角三角形、钝角三角形和直角三角形有几条角平分线?
因为线段AD是△ ABC BC边上的角平分线.所以 。线段顶点与对边中点猜测在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。三角形的三条角平分线相交于一点,交点在三角形的内部思考:高和中线还可以说成边的高线和中线(如AD是BC边的高)但三角形的角平分线是不可以说成某个角的角平分线(如AD是△ABC的角平分线但不是∠BAC的角平分线)你知道为什么吗?今天所研究的都是线段三角形的角平分线是一条线段 , 角的平分线是一条射线.三角形的一个角的平分线叫做三角形的角平分线.( )
判断×动手完成学案上合作交流的部分课堂练习2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形BD课本5页2题 投影展示在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.ADBC比一比如图AD 是△ABC中BC上的中线,则S△ABD S△ACD =拓展训练三角形的中线将三角形分成面积相等的两个三角形当堂检测2、如图,CA⊥DA于A,C在BD的延长线上,则正确的是( )
A、CA是BC边上的高 B、CA是AB边上的高
C、CA是AD边上的高 D、BA是AC边上的高
3、如图,AD、AE分别是△ABC的中线和高,BC=6cm,AE=4cm,△ABC的面为 ,△ABD的面积为 , △ADC的面积为 ,
C1266三角形的稳定性课本7页练习 用三根木棒钉一个三角形,你会发现再也无法改变这个
三角形的形状和大小,也就是说,如果一个三角形的
三条边固定了,那么三角形的形状和大小就完全确定了.
在数学上把三角形的这个性质叫做三角形的稳定性.三角形的稳定性在生活中有广泛的应用 ,你能举出一些例子吗?练一练1、下列图形中具有稳定性的是( )(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形C2、要使下列木架不稳定各至少需要多少根木棍?3、下列图中具有稳定性有( )A 1个 B 2个 C 3个 D 4个C已知一个等腰三角形的周长为20cm,其中一边长为4cm,求另外两边的长?解:当4cm为底边,设腰长为x cm,则4+2x=20,解得 x=8 (这样的三角形存在吗?)当4cm为腰,设底边长为x cm,则 2×4+x=20,解得 x=12 (这样的三角形存在吗?)因为 4+4<12,所以腰为4不可能。
综上所述 ,另外两边的长为8cm、8cm。新知应用现在有长度为3cm、5cm的两根小木棒,请你选择第三根木棒使他们能摆成三角形,你选择的木棒是多长?你知道第三根木棒的选择有什么要求吗?解:设第三根木棒的长度为a cm 则有
5-3即 2则化简|a+b–c|的结果是_________a+b–c当堂检测1、 已知等腰三角的两边分别是4厘米和7厘米,则此
三角形的周长是( )
A、15厘米 B、18厘米
C、15厘米或18厘米 D、无法确定
2、已知四组线段的长度分别如下,以各组线段为边能
构成三角形的是( )
A、1㎝,2㎝,4㎝ B、8㎝,6㎝,4㎝
C、12㎝,5㎝,6㎝ D、2㎝,3㎝,6㎝
3、 已知等腰三角形的两边长分别为3和6,则周长为( )
A、9 B、12 C、15 D、12或15
选做、长为10,7,5,3的四根木条,选其中三根组
成三角形,有几种选法?写出全部情况 CBC别忘了作业一、作业本:课本8页习题11.1的4、8题。
选作:课本9页9题二、导学案完善与预习
【知识链接】1、如图,AB∥ED,
则图中相等的角有 ;
2、如图,E 是BA延长线上一点,AD∥BC,则图中相等的角有 .∠ACD=∠D,∠BCE=∠E∠EAD=∠B,∠CAD=∠CE.D.证法一证法二 则 C E∥B A ﹙内错角相等,两直线平行﹚
∴ ∠D C E =∠B ﹙两直线平行,同位角相等﹚
∵ ∠B C A +∠A C E +∠E C D =180°﹙平角定义﹚ zxxk
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚已知:△A B C.
求证:∠A +∠B +∠C=180°证明:延长B C至D ,过点C作CE∥ABA.B.学案上课堂练习1(比一比谁做得又对又快)1、在△ABC中,若∠A=80°, ∠C=20°,则∠B= 。
2、在△ABC中,若∠A=80° ,∠B= ∠C,
则∠B= 。80°50°例 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线。求∠ADB的度数合作交流能动手的自己独立完成,不能完成的可参照下边的提示做 z.xxk1、把已知的度数在图上标示一下
2、看所求的角在哪个三角形中,在这个三角形中另外两个角知道了吗?
课堂训练:课本13页1、2题,选作,已知等腰三角形的一个角分别为50°则另外两个角的度数为 。 50°、 80°或 65°、6 5°除学案外,完成课本8、9页的题 1、从A处观测C处的仰角∠CAB =30°,从B处观测C处时仰角∠CB D=45°,从C处观测A、B两处时的视角∠ACB 是多少度?练 习 2、如图,一种滑翔伞的形
状是左右对称的四边形ABCD,
其中∠A =150°, ∠B = ∠D= 40°, 求∠C的度数.选作、证明:四边形的内角和
为360o.别忘了作业一、作业本:课本28页习题复习题的6题。二、导学案完善与预习:(自主学习与知识链接部分)
三、纠错:已批改过的导学案的纠错
∴ ∠1 =∠B ﹙两直线平行,内错角相等﹚
∠2 =∠C
∠1 +∠2 +∠3 =180°﹙平角定义﹚
∴ ∠B +∠C +∠B AC= 180° ﹙ 等量代换﹚已知:△A B C.
求证:∠A +∠B +∠C=180°证明:过点A作 ∥ ,A知识链接123自学检测 zxxk1、如何证明“直角三角形的两锐角互余”已知:在直角三角形ABC中, ∠C =90°。
求证: ∠A+ ∠B =90°证明:在△ABC中,
∵∠A+ ∠B +∠C =180°,而∠C =90°
∴ ∠A+ ∠B = 180° -90°= 90°你能用符号记一下吗?Rt △ABC1、在Rt△ABC中, ∠C=90°,∠A=50°,∠B= 。2、下列说法正确的有 :①直角三角形中的两个角互余;②直角三角形中的两个角互补;③直角三角形中的两个锐角互余;④直角三角形中的两个锐角的和是90°.50°③ ④归纳自学内容,你知道了什么?【合作交流】例 如图,∠C=∠D =90°,AD,BC相交于点E, ∠CAE 与∠DBE有什么关系?为什么?会做的同学整理思路准备给同学讲;不会做的同学看老师下面的提示① ∠CAE与∠DBE在同一个三角形中吗?
② ∠CAE在哪个三角形中,它可以表示为
∠DBE在哪个三角形中,它可以表示为思考:如果是直角三角形则两锐角互余,反之,如果在一个三角形中两角互余,则这个三角形是直角三角形吗? Z.xxk已知:在三角形ABC中,∠ A+ ∠B=90°。
求证: ∠C =90°证明:在△ABC中,
∵∠A+ ∠B +∠C =180°,
而∠A+ ∠B =90°
∴ ∠C =90°【课堂练习】1、课本14页1题,
变式你还能说一下∠A与∠BCD的关系吗?
选作请你找出图中所有的互余的角并写下来解:∠B=∠ACD。理由:
在Rt △ABC中, ∠ACB =90°
∴ ∠B= 90°— ∠A
∵CD⊥AB
∴ △ACD是直角三角形
∴∠ACD= 90°— ∠A
∴ ∠B=∠ACD
课本14页2题【拓展训练】例1: 如图,C岛在A岛的北偏东 方向,B岛在A岛的北偏东 方向,C岛在B岛的北偏西 方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?会做的同学整理思路
准备给同学讲;
不会做的同学看老师
下面的提示在图上把已知角的度数标识小结
把条件集中在一个三角形中,有时需要研究几个三角形
注意和平行线的性质结合使用来求角的度数 zx.xk别忘了作业一、作业本:课本28页习题复习题的6题。二、导学案完善与预习:(自主学习与知识链接部分)
三、纠错:已批改过的导学案的纠错
2、已知OC 是∠AOB的角平分线,zxxk
则∠AOB =_______。知识链接
你还记得 “过一点画已知
直线的垂线” 吗?自学教材4页第一自然段的内容,完成学案并思考如下问题
1、三角形的高线是 。Z.xxk
2、三角形的高线的两端点是 。
3、几何语言:知识链接
因为线段AD是△ ABC 的BC边上的高.所以 AD BC 。线段顶点与对边垂足(或 =90°) ∠ADC 锐角三角形的三条高(2) 这三条高之间有怎样的位置关系?锐角三角形的三条高是
在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部。直角三角形的三条高 将你的结果与同伴进行交流.ABC直角边BC边上的高是__________; AB直角边AB边上的高是 ;CB(2)它们有怎样的位置关系?D斜边AC边上的高是______________. BD●直角三角形的三条高
交于直角顶点.钝角三角形的三条高(1) 钝角三角形的
三条高交于一点吗?(2)它们所在的直线交于一点吗?O钝角三角形的三条高
不相交于一点.钝角三角形的三条高
所在直线交于一点.小结:三角形的高311相交相交不相交相交相交相交三角形的三条高所在直线交于一点三角形内部直角顶点三角形外部自学课本4页剩下部分到5页的内容完成学案并思考如下问题
1、三角形的中线是 。
2、三角形的中线的两端点是 。
3、几何语言:
4、锐角三角形、钝角三角形和直角三角形有几条中线?
知识链接
因为线段AD是△ ABC BC边上的中线.所以 。线段顶点与对边中点=导学案
1、分别画出各个三角形的中线。
2、观察每个三角形你所画的三条中线,你发现了什么?
3、通过折纸验证你的发现。Zx.xk
D●●三角形的三条中线相交于一点,交点在三角形的内部.EFO合作交流三角形的重心为什么叫做重心?1、三角形的角平分线是 。
2、三角形的角平分线的两端点是 。
3、几何语言:
4、锐角三角形、钝角三角形和直角三角形有几条角平分线?
因为线段AD是△ ABC BC边上的角平分线.所以 。线段顶点与对边中点猜测在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。三角形的三条角平分线相交于一点,交点在三角形的内部思考:高和中线还可以说成边的高线和中线(如AD是BC边的高)但三角形的角平分线是不可以说成某个角的角平分线(如AD是△ABC的角平分线但不是∠BAC的角平分线)你知道为什么吗?今天所研究的都是线段三角形的角平分线是一条线段 , 角的平分线是一条射线.三角形的一个角的平分线叫做三角形的角平分线.( )
判断×动手完成学案上合作交流的部分课堂练习2.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形BD课本5页2题 投影展示在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.ADBC比一比如图AD 是△ABC中BC上的中线,则S△ABD S△ACD =拓展训练三角形的中线将三角形分成面积相等的两个三角形当堂检测2、如图,CA⊥DA于A,C在BD的延长线上,则正确的是( )
A、CA是BC边上的高 B、CA是AB边上的高
C、CA是AD边上的高 D、BA是AC边上的高
3、如图,AD、AE分别是△ABC的中线和高,BC=6cm,AE=4cm,△ABC的面为 ,△ABD的面积为 , △ADC的面积为 ,
C1266三角形的稳定性课本7页练习 用三根木棒钉一个三角形,你会发现再也无法改变这个
三角形的形状和大小,也就是说,如果一个三角形的
三条边固定了,那么三角形的形状和大小就完全确定了.
在数学上把三角形的这个性质叫做三角形的稳定性.三角形的稳定性在生活中有广泛的应用 ,你能举出一些例子吗?练一练1、下列图形中具有稳定性的是( )(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形C2、要使下列木架不稳定各至少需要多少根木棍?3、下列图中具有稳定性有( )A 1个 B 2个 C 3个 D 4个C已知一个等腰三角形的周长为20cm,其中一边长为4cm,求另外两边的长?解:当4cm为底边,设腰长为x cm,则4+2x=20,解得 x=8 (这样的三角形存在吗?)当4cm为腰,设底边长为x cm,则 2×4+x=20,解得 x=12 (这样的三角形存在吗?)因为 4+4<12,所以腰为4不可能。
综上所述 ,另外两边的长为8cm、8cm。新知应用现在有长度为3cm、5cm的两根小木棒,请你选择第三根木棒使他们能摆成三角形,你选择的木棒是多长?你知道第三根木棒的选择有什么要求吗?解:设第三根木棒的长度为a cm 则有
5-3
三角形的周长是( )
A、15厘米 B、18厘米
C、15厘米或18厘米 D、无法确定
2、已知四组线段的长度分别如下,以各组线段为边能
构成三角形的是( )
A、1㎝,2㎝,4㎝ B、8㎝,6㎝,4㎝
C、12㎝,5㎝,6㎝ D、2㎝,3㎝,6㎝
3、 已知等腰三角形的两边长分别为3和6,则周长为( )
A、9 B、12 C、15 D、12或15
选做、长为10,7,5,3的四根木条,选其中三根组
成三角形,有几种选法?写出全部情况 CBC别忘了作业一、作业本:课本8页习题11.1的4、8题。
选作:课本9页9题二、导学案完善与预习
【知识链接】1、如图,AB∥ED,
则图中相等的角有 ;
2、如图,E 是BA延长线上一点,AD∥BC,则图中相等的角有 .∠ACD=∠D,∠BCE=∠E∠EAD=∠B,∠CAD=∠CE.D.证法一证法二 则 C E∥B A ﹙内错角相等,两直线平行﹚
∴ ∠D C E =∠B ﹙两直线平行,同位角相等﹚
∵ ∠B C A +∠A C E +∠E C D =180°﹙平角定义﹚ zxxk
∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚已知:△A B C.
求证:∠A +∠B +∠C=180°证明:延长B C至D ,过点C作CE∥ABA.B.学案上课堂练习1(比一比谁做得又对又快)1、在△ABC中,若∠A=80°, ∠C=20°,则∠B= 。
2、在△ABC中,若∠A=80° ,∠B= ∠C,
则∠B= 。80°50°例 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线。求∠ADB的度数合作交流能动手的自己独立完成,不能完成的可参照下边的提示做 z.xxk1、把已知的度数在图上标示一下
2、看所求的角在哪个三角形中,在这个三角形中另外两个角知道了吗?
课堂训练:课本13页1、2题,选作,已知等腰三角形的一个角分别为50°则另外两个角的度数为 。 50°、 80°或 65°、6 5°除学案外,完成课本8、9页的题 1、从A处观测C处的仰角∠CAB =30°,从B处观测C处时仰角∠CB D=45°,从C处观测A、B两处时的视角∠ACB 是多少度?练 习 2、如图,一种滑翔伞的形
状是左右对称的四边形ABCD,
其中∠A =150°, ∠B = ∠D= 40°, 求∠C的度数.选作、证明:四边形的内角和
为360o.别忘了作业一、作业本:课本28页习题复习题的6题。二、导学案完善与预习:(自主学习与知识链接部分)
三、纠错:已批改过的导学案的纠错
∴ ∠1 =∠B ﹙两直线平行,内错角相等﹚
∠2 =∠C
∠1 +∠2 +∠3 =180°﹙平角定义﹚
∴ ∠B +∠C +∠B AC= 180° ﹙ 等量代换﹚已知:△A B C.
求证:∠A +∠B +∠C=180°证明:过点A作 ∥ ,A知识链接123自学检测 zxxk1、如何证明“直角三角形的两锐角互余”已知:在直角三角形ABC中, ∠C =90°。
求证: ∠A+ ∠B =90°证明:在△ABC中,
∵∠A+ ∠B +∠C =180°,而∠C =90°
∴ ∠A+ ∠B = 180° -90°= 90°你能用符号记一下吗?Rt △ABC1、在Rt△ABC中, ∠C=90°,∠A=50°,∠B= 。2、下列说法正确的有 :①直角三角形中的两个角互余;②直角三角形中的两个角互补;③直角三角形中的两个锐角互余;④直角三角形中的两个锐角的和是90°.50°③ ④归纳自学内容,你知道了什么?【合作交流】例 如图,∠C=∠D =90°,AD,BC相交于点E, ∠CAE 与∠DBE有什么关系?为什么?会做的同学整理思路准备给同学讲;不会做的同学看老师下面的提示① ∠CAE与∠DBE在同一个三角形中吗?
② ∠CAE在哪个三角形中,它可以表示为
∠DBE在哪个三角形中,它可以表示为思考:如果是直角三角形则两锐角互余,反之,如果在一个三角形中两角互余,则这个三角形是直角三角形吗? Z.xxk已知:在三角形ABC中,∠ A+ ∠B=90°。
求证: ∠C =90°证明:在△ABC中,
∵∠A+ ∠B +∠C =180°,
而∠A+ ∠B =90°
∴ ∠C =90°【课堂练习】1、课本14页1题,
变式你还能说一下∠A与∠BCD的关系吗?
选作请你找出图中所有的互余的角并写下来解:∠B=∠ACD。理由:
在Rt △ABC中, ∠ACB =90°
∴ ∠B= 90°— ∠A
∵CD⊥AB
∴ △ACD是直角三角形
∴∠ACD= 90°— ∠A
∴ ∠B=∠ACD
课本14页2题【拓展训练】例1: 如图,C岛在A岛的北偏东 方向,B岛在A岛的北偏东 方向,C岛在B岛的北偏西 方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?会做的同学整理思路
准备给同学讲;
不会做的同学看老师
下面的提示在图上把已知角的度数标识小结
把条件集中在一个三角形中,有时需要研究几个三角形
注意和平行线的性质结合使用来求角的度数 zx.xk别忘了作业一、作业本:课本28页习题复习题的6题。二、导学案完善与预习:(自主学习与知识链接部分)
三、纠错:已批改过的导学案的纠错
