人教版九年级下册27.1图形的相似课件(共25张PPT)
文档属性
| 名称 | 人教版九年级下册27.1图形的相似课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 244.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-23 15:28:54 | ||
图片预览






文档简介
(共25张PPT)
1、 叫做相似图形。
形状相同的图形
即两个图形只是形状相同、与大小无关。
∽
相似于
3、相似图形与全等图形有哪些区别与联系?
相似图形只要求形状相同,与大小无关;
全等图形必须是形状相同,大小相同。
所以:相似图形不一定是全等,全等图形一定是相似。
知识回顾:
2、两个相似的图形用 数学符号表示,读作 。
两个全等三角形对应边相等,对应角相等,那么两个相似的多边形之间有什么关系呢?相似多边形有什么主要特征呢?
大胆猜想:
如果两个图形相似,它们的对应边、对应角可能存在怎样的关系?
问题情境:
问题1:
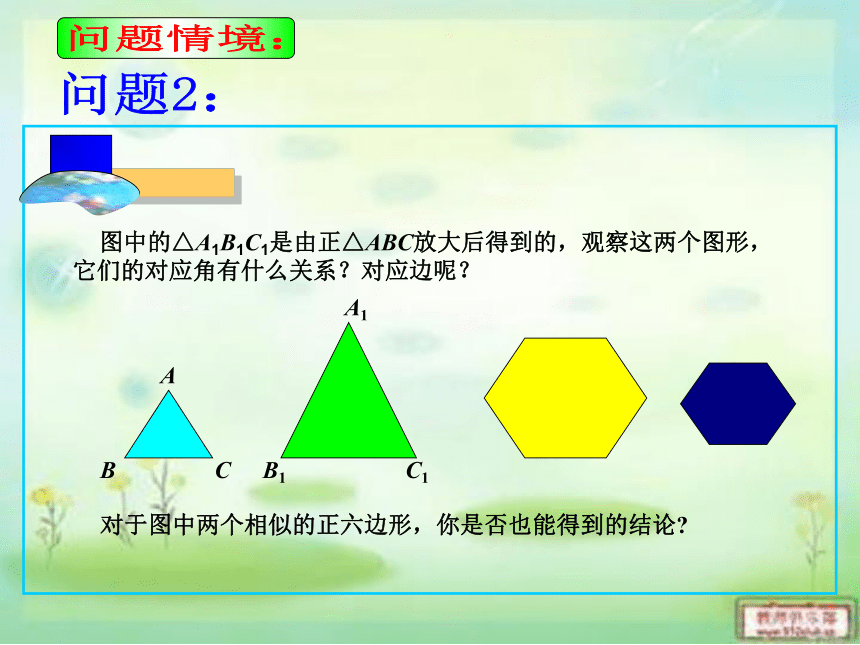
图中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
对于图中两个相似的正六边形,你是否也能得到的结论
C
A
B
C1
A1
B1
问题情境:
问题2:
对比图中的△A1B1C1和△ABC,由于正三角形的每个角都等于60 ° ,可得
∠A=∠A1,∠B=∠B1,∠C=∠C1
由△ABC和△A1B1C1都是正三角形可得:
AB=BC=AC, A1B1=B1C1=A1C1
这说明:正三角形都是相似的,它们的对应角
相等,对应边的比相等.
相似的正多边形对应角相等,对应边的比相等.
这个结论对于一般的相似多边形是否成立呢?
图中的两个相似的正六边形,也有类似的结论.
对于四条线段a、b、c、d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc)我们就说这四条是成比例线段,简称比例线段.
27.1 图形的相似(二)
义务教育课程标准实验教科书
九年级 下册
学 习 目 标
3、会根据相似多边形的特征识别两个多边
形是否相似,并会运用其性质进行相关的计算。
1、了解成比例线段的概念,会确定线段
的比;
2、知道相似多边形的主要特征,即:相
似多边形的对应角相等,对应边的比相等 ;
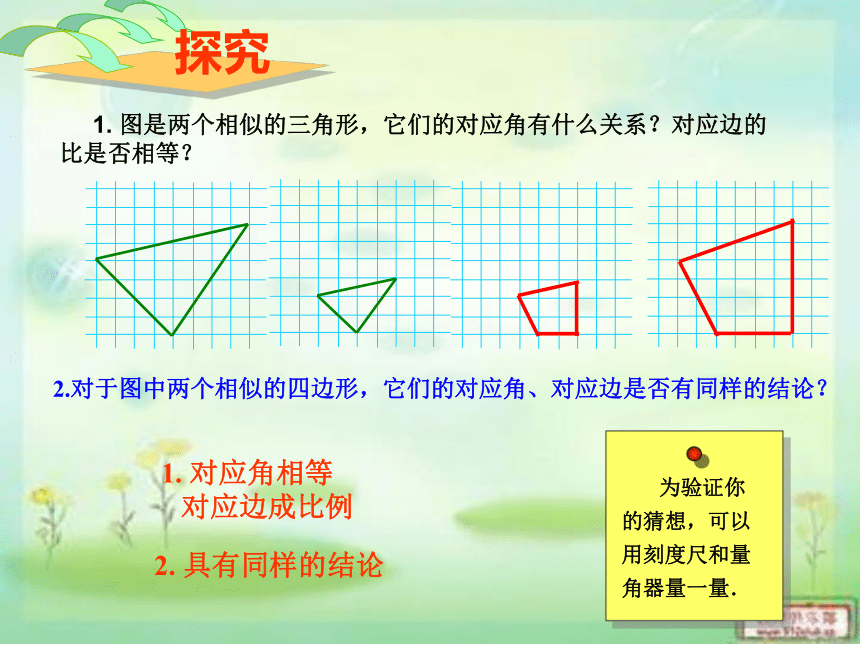
1. 图是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?
探究
2.对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?
为验证你的猜想,可以用刻度尺和量角器量一量.
1. 对应角相等
对应边成比例
2. 具有同样的结论
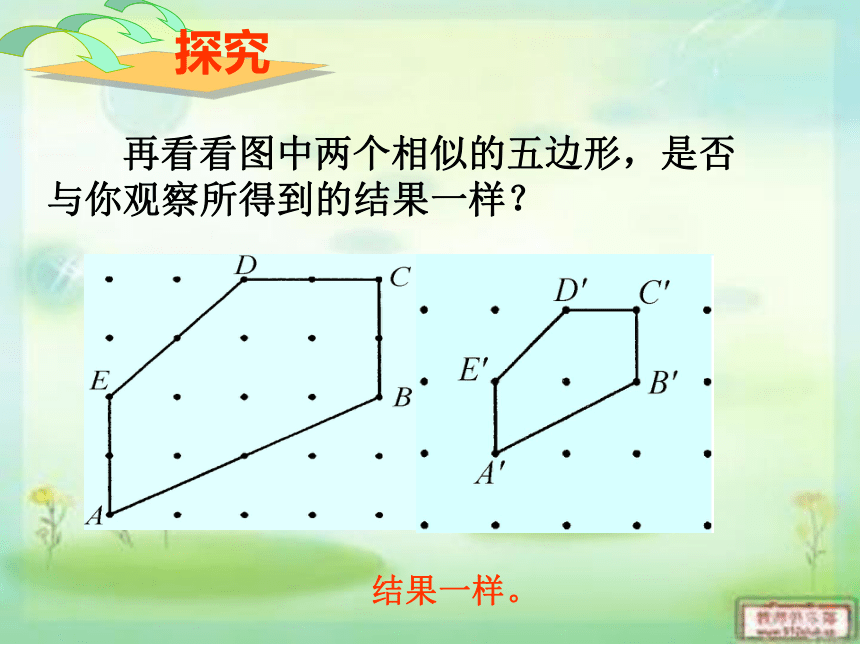
再看看图中两个相似的五边形,是否
与你观察所得到的结果一样?
探究
结果一样。
相似多边形性质:
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.
相似比: 我们把相似多边形对应边的比称为相似比.
相似多边形的判定方法:
相似比为1时,相似的两个图形有什么关系?
两图形全等
结论:
相似多边形对应角相等,对应边的比相等。
下图是两个等边三角形,找出图形中的
成比例线段,并用比例式表示.
两个任意三角形是相似图形吗?
两个任意等腰三角形呢?
想一想:
不一定是相似图形。如果有对应角相等,对应边成比例,就是相似图形。
也不一定相似。两个等腰三角形如果有一组对应角相等,两组对应边成比例,这两个等腰三角形就是相似三角形。
例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得:
解得 x=28(cm)
∠α=∠C=83°,∠A=∠E=118°
在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°.
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
1. 在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离
设两地的实际距离为x
x = 300000000
x = 3000千米
答: 甲,乙两地的实际距离为30000千米。
解:
课 堂 练 习
根据比例尺
2. 如图所示的两个三角形一定相似吗?为什么?
5
5
10
不 一 定 相 似。
10
课 堂 练 习
3. 如图所示的两个五边形相似,求未知边a、b、
c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示: 可知两图形的相似比为:
∴
b = 4.5
a = 3
c = 4
d = 6
课 堂 练 习
4、判断:
1、所有的等腰三角形都相似( )
2、所有的等边三角形都相似( )
3、所有直角三角形都相似( )
4、所有的等腰直角三角形都相似( )
×
√
×
√
课 堂 练 习
5、如图,DE∥BC,求
△ADE与△ABC相似吗?为什么
相似。
因为对应角相等,对应边的比也相等。
课 堂 练 习
6、 如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
易错题
∴不相似。
课 堂 练 习
7、如下图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形。
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
动动手
课 堂 练 习
成比例线段的概念及线段的比。
课堂小结
相似多边形
特征
识别
对应角相等
对应边的比相等
本节课,我们学习了哪些知识?
你还有哪些困惑?
相似多边形性质。
相似多边形的判定方法。
运用其性质进行相关的计算。
相似多边形的特征和识别:
1、如图,△ABC与△DEF相似,求未知边x,y的长度。
达标测试
2、已知:ΔABC ∽ ΔADE,其中∠ADE= ∠B,写出对应边的比例式。
A
D
E
C
B
3、在如图所示的相似四边形中, 求未知边x、 y的长度和角度a的大小。
(30′)
(30′)
(40′)
1、如图,△ABC与△DEF相似,求未知边x,y的长度。
解得:x=6
y=3.5
达标测试答案
解:∵ △ABC与△DEF相似,它们的对应边成比例,对应角相等,所以
3、 在如图所示的相似四边形中, 求未知边x、
y的长度和角度a的大小.
解:由于两个四边形相似,它们的对应边成比例,对应角相等,所以
解得 x=31.5,y=27
a =360°-(77°+83°+117°)=83°
达标测试答案
预 习 作 业
1、自学课本第40——42页的课
文内 容。
2、完成第54页习题27.2 1、4、
5题。
3、完成练习册第 页 题。
谢谢合作!
1、 叫做相似图形。
形状相同的图形
即两个图形只是形状相同、与大小无关。
∽
相似于
3、相似图形与全等图形有哪些区别与联系?
相似图形只要求形状相同,与大小无关;
全等图形必须是形状相同,大小相同。
所以:相似图形不一定是全等,全等图形一定是相似。
知识回顾:
2、两个相似的图形用 数学符号表示,读作 。
两个全等三角形对应边相等,对应角相等,那么两个相似的多边形之间有什么关系呢?相似多边形有什么主要特征呢?
大胆猜想:
如果两个图形相似,它们的对应边、对应角可能存在怎样的关系?
问题情境:
问题1:
图中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
对于图中两个相似的正六边形,你是否也能得到的结论
C
A
B
C1
A1
B1
问题情境:
问题2:
对比图中的△A1B1C1和△ABC,由于正三角形的每个角都等于60 ° ,可得
∠A=∠A1,∠B=∠B1,∠C=∠C1
由△ABC和△A1B1C1都是正三角形可得:
AB=BC=AC, A1B1=B1C1=A1C1
这说明:正三角形都是相似的,它们的对应角
相等,对应边的比相等.
相似的正多边形对应角相等,对应边的比相等.
这个结论对于一般的相似多边形是否成立呢?
图中的两个相似的正六边形,也有类似的结论.
对于四条线段a、b、c、d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如 (即ad=bc)我们就说这四条是成比例线段,简称比例线段.
27.1 图形的相似(二)
义务教育课程标准实验教科书
九年级 下册
学 习 目 标
3、会根据相似多边形的特征识别两个多边
形是否相似,并会运用其性质进行相关的计算。
1、了解成比例线段的概念,会确定线段
的比;
2、知道相似多边形的主要特征,即:相
似多边形的对应角相等,对应边的比相等 ;
1. 图是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?
探究
2.对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?
为验证你的猜想,可以用刻度尺和量角器量一量.
1. 对应角相等
对应边成比例
2. 具有同样的结论
再看看图中两个相似的五边形,是否
与你观察所得到的结果一样?
探究
结果一样。
相似多边形性质:
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似.
相似比: 我们把相似多边形对应边的比称为相似比.
相似多边形的判定方法:
相似比为1时,相似的两个图形有什么关系?
两图形全等
结论:
相似多边形对应角相等,对应边的比相等。
下图是两个等边三角形,找出图形中的
成比例线段,并用比例式表示.
两个任意三角形是相似图形吗?
两个任意等腰三角形呢?
想一想:
不一定是相似图形。如果有对应角相等,对应边成比例,就是相似图形。
也不一定相似。两个等腰三角形如果有一组对应角相等,两组对应边成比例,这两个等腰三角形就是相似三角形。
例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得:
解得 x=28(cm)
∠α=∠C=83°,∠A=∠E=118°
在四边形ABCD中,∠β=360°-(78°+83°+118°)=81°.
D
A
B
C
18cm
21cm
78°
83°
β
24cm
G
E
F
H
α
x
118°
1. 在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离
设两地的实际距离为x
x = 300000000
x = 3000千米
答: 甲,乙两地的实际距离为30000千米。
解:
课 堂 练 习
根据比例尺
2. 如图所示的两个三角形一定相似吗?为什么?
5
5
10
不 一 定 相 似。
10
课 堂 练 习
3. 如图所示的两个五边形相似,求未知边a、b、
c、d的长度.
5
3
2
c
d
7.5
b
a
6
9
解:由图示: 可知两图形的相似比为:
∴
b = 4.5
a = 3
c = 4
d = 6
课 堂 练 习
4、判断:
1、所有的等腰三角形都相似( )
2、所有的等边三角形都相似( )
3、所有直角三角形都相似( )
4、所有的等腰直角三角形都相似( )
×
√
×
√
课 堂 练 习
5、如图,DE∥BC,求
△ADE与△ABC相似吗?为什么
相似。
因为对应角相等,对应边的比也相等。
课 堂 练 习
6、 如图矩形草坪长20m,宽10m,沿草坪四周有1m宽的环形小路,小路内外边缘所成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
易错题
∴不相似。
课 堂 练 习
7、如下图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形。
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
动动手
课 堂 练 习
成比例线段的概念及线段的比。
课堂小结
相似多边形
特征
识别
对应角相等
对应边的比相等
本节课,我们学习了哪些知识?
你还有哪些困惑?
相似多边形性质。
相似多边形的判定方法。
运用其性质进行相关的计算。
相似多边形的特征和识别:
1、如图,△ABC与△DEF相似,求未知边x,y的长度。
达标测试
2、已知:ΔABC ∽ ΔADE,其中∠ADE= ∠B,写出对应边的比例式。
A
D
E
C
B
3、在如图所示的相似四边形中, 求未知边x、 y的长度和角度a的大小。
(30′)
(30′)
(40′)
1、如图,△ABC与△DEF相似,求未知边x,y的长度。
解得:x=6
y=3.5
达标测试答案
解:∵ △ABC与△DEF相似,它们的对应边成比例,对应角相等,所以
3、 在如图所示的相似四边形中, 求未知边x、
y的长度和角度a的大小.
解:由于两个四边形相似,它们的对应边成比例,对应角相等,所以
解得 x=31.5,y=27
a =360°-(77°+83°+117°)=83°
达标测试答案
预 习 作 业
1、自学课本第40——42页的课
文内 容。
2、完成第54页习题27.2 1、4、
5题。
3、完成练习册第 页 题。
谢谢合作!
